专项训练卷(三) 几何题的说理 闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 专项训练卷(三) 几何题的说理 闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
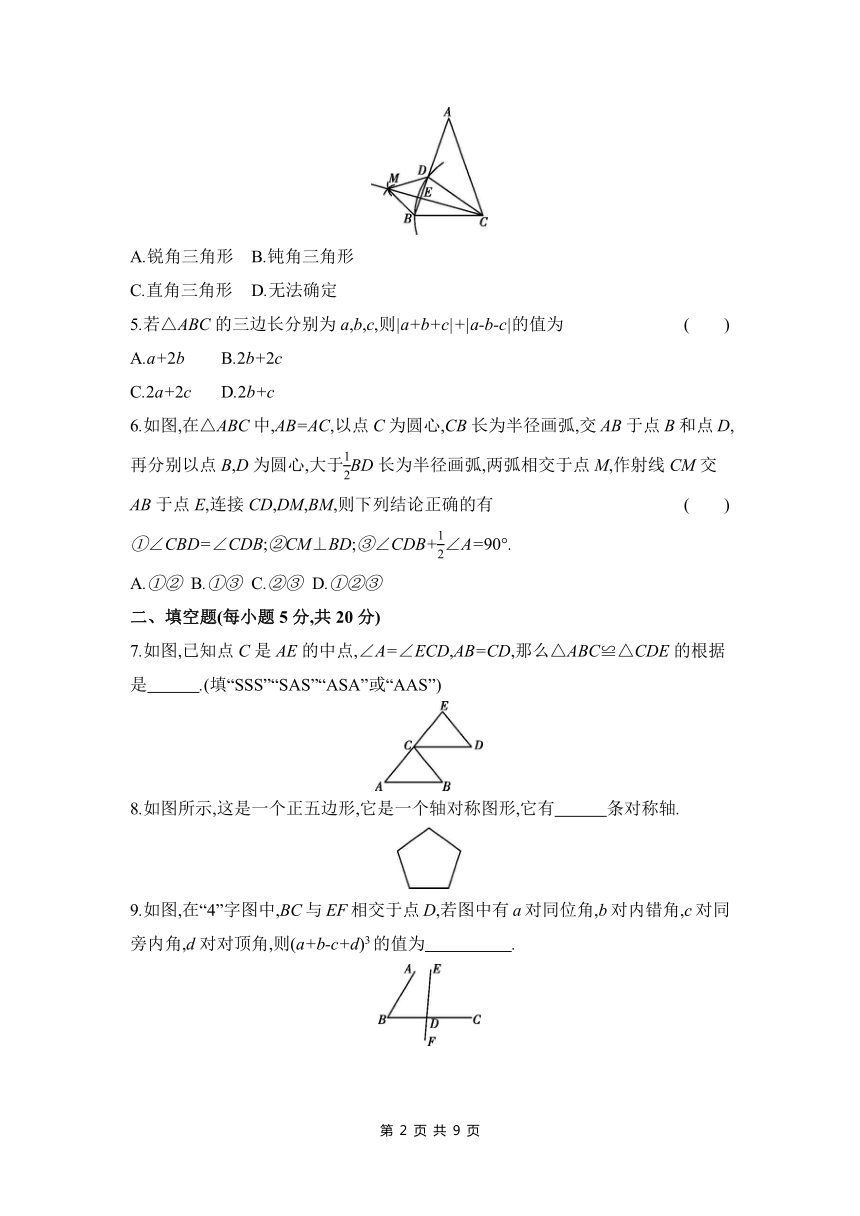
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 11:45:29 | ||
图片预览


文档简介
专项训练卷(三) 几何题的说理
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题5分,共30分)
1.如图,已知直线l上有一点A,直线m⊥n,则∠1与∠2的关系是 ( )
A.∠1与∠2相等 B.∠1与∠2互余
C.∠1与∠2互补 D.∠1与∠2是对顶角
2.如图,已知点D,B在线段AE上,若∠ABC=∠E,则下列结论正确的是 ( )
A.AC∥DF B.BD∥AC
C.BC∥EF D.DG∥AC
3.将一副三角板和一张对边平行的纸条按如图所示的方式摆放,两把三角板的一条直角边重合,则∠1与∠2之间的数量关系是 ( )
A.∠1+∠2=30° B.∠1+∠2=45°
C.∠1+∠2=60° D.2∠1+∠2=75°
4.在△ABC中,若∠A=2∠B,∠A=∠C+20°,则△ABC的形状是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.无法确定
5.若△ABC的三边长分别为a,b,c,则|a+b+c|+|a-b-c|的值为 ( )
A.a+2b B.2b+2c
C.2a+2c D.2b+c
6.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E,连接CD,DM,BM,则下列结论正确的有 ( )
①∠CBD=∠CDB;②CM⊥BD;③∠CDB+∠A=90°.
A.①② B.①③ C.②③ D.①②③
二、填空题(每小题5分,共20分)
7.如图,已知点C是AE的中点,∠A=∠ECD,AB=CD,那么△ABC≌△CDE的根据是 .(填“SSS”“SAS”“ASA”或“AAS”)
8.如图所示,这是一个正五边形,它是一个轴对称图形,它有 条对称轴.
9.如图,在“4”字图中,BC与EF相交于点D,若图中有a对同位角,b对内错角,c对同旁内角,d对对顶角,则(a+b-c+d)3的值为 .
10.如图,已知AB∥CD,AE⊥EF,则∠A,∠C,∠F之间的数量关系是 .
三、解答题(本大题5小题,共50分)
11.(8分)如图,直线AB与EF相交于点O.
(1)若∠AOE=45°,∠AOF=3∠COF,试说明AB⊥CO;
(2)在(1)的条件下,找出所有与∠COF互余的角和互补的角.
12.(8分)如图,已知在Rt△ABC中,∠C=90°.
(1)尺规作图(保留作图痕迹,标明字母):
①作∠ACB的平分线CD,交AB于点D;
②延长BC到点E,使得CE=CA,连接AE.
(2)试判断CD与AE的位置关系,并说明理由.
13.(8分)如图,在Rt△ABC中,∠B=90°,AD是∠BAC的平分线,DE⊥AC于点E,点F是AB上一点,BF=CE.
(1)△BDF和△EDC全等吗 请说明理由.
(2)试猜想AC,AB,BF之间的数量关系,并说明理由.
14.(12分)如图,已知点P,Q分别在直线AB,CD上,∠APN+∠PNQ+∠CQN=360°.
(1)试说明AB∥CD;
(2)若PM,QM分别平分∠BPN,∠DQN,试探究∠M与∠N之间的数量关系,并说明理由.
15.(14分)阅读材料,完成后面的任务:
材料:如图1,在凹四边形ABOC中,试探究∠BOC与∠A,∠B,∠C之间的数量关系.小明发现并提供了如下方法:
解:∠BOC=∠A+∠B+∠C.如图2,连接AO并延长,因为∠1+∠B+∠AOB=180°,∠3+∠AOB=180°,所以∠3=∠1+∠B,同理∠4=∠2+∠C,所以∠3+∠4=∠1+∠2+∠B+∠C,所以∠BOC=∠BAC+∠B+∠C.
任务:(1)你有与小明不同的方法吗 请写出你的解答过程.
(2)如图3所示,根据图中标注的角的度数,请说明∠A+∠C+∠D+∠F=230°.
(3)如图4所示,在△ABC中,AB=AC,∠ABC,∠ACB的平分线BD,CE交于点O,∠EOD+∠OBF=180°,BF交AC的延长线于点F,∠CDG=∠F,DG交BC的延长线于点G,找出图中的平行线,并说明理由.
(4)在(3)的条件下,若∠A=58°,直接写出∠ADG的度数: .
参考答案
一、选择题
1 2 3 4 5 6
B C B A B D
1.B 【解析】因为∠1+∠2=180°-90°=90°,所以∠1与∠2互余.
2.C 【解析】因为∠ABC=∠E,所以BC∥EF.
3.B 【解析】如图,过点F作HF∥AB,因为AB∥CD,所以HF∥AB∥CD,所以∠1=∠EFH,∠2=∠GFH,所以∠1+∠2=∠EFG=45°.
4.A 【解析】设∠B=x,则∠A=2x,∠C=2x-20°,因为∠A+∠B+∠C=180°,所以2x+x+2x-20°=180°,解得x=40°,所以∠A=80°,∠B=40°,∠C=60°,所以△ABC是锐角三角形.
5.B 【解析】原式=a+b+c+b+c-a=2b+2c.
6.D 【解析】①由作图可知,CB=CD,所以△CBD是等腰三角形,所以∠CBD=∠CDB,正确;②由作图可知,DM=BM,CB=CD,因为CM=CM,所以△CBM≌△CDM,所以∠DCM=∠BCM,所以CM⊥BD,正确;③因为AB=AC,所以∠CBD=∠ACB,因为∠CBD+∠ACB+∠A=180°,所以2∠CBD+∠A=180°,所以∠CBD+∠A=90°,因为∠CBD=∠CDB,所以∠CDB+∠A=90°,正确.
二、填空题
7.SAS
8.5
9.27 【解析】由图可知a=1,b=1,c=1,d=2,所以(a+b-c+d)3=(1+1-1+2)3=27.
10.∠A+∠C+∠EFC=270° 【解析】 如图,过点F作FG∥AB,因为AB∥CD,所以FG∥AB∥CD,同理,过点E作EH∥AB,则EH∥AB∥CD,所以∠A=∠AEH,∠EFG=∠FEH,即∠A+∠EFG=∠AEF=90°,因为∠GFC+∠C=180°,所以∠A+∠EFC+∠C=90°+180°=270°.
三、解答题
11.解:(1)因为∠AOE=45°,所以∠BOF=∠AOE=45°,所以∠AOF=180°-45°=135°,因为∠AOF=3∠COF,所以3∠COF=135°,所以∠COF=45°,所以∠COB=90°,
所以AB⊥CO. (4分)
(2)与∠COF互余的角:∠BOF,∠AOE;与∠COF互补的角:∠COE. (8分)
12.解:(1)如图所示: (4分)
(2)因为AC=CE,AC⊥CE,
所以△ACE是等腰直角三角形,
所以∠CAE=45°, (6分)
因为CD平分∠ACB,所以∠ACD=45°,
所以∠ACD=∠CAE,所以CD∥AE. (8分)
技巧点拨 本题属于作图与说理为一体的几何问题,猜想结论性问题是中考的一大亮点问题,在第(2)小问中,只要作图准确,就可得出正确的结论.两直线的位置关系主要有两种:一是平行,二是垂直.要说明两直线平行,只需说明同位角相等或内错角相等或同旁内角互补.
13.解:(1)△BDF≌△EDC. (1分)
理由:因为∠B=90°,AD是∠BAC的平分线,DE⊥AC,
所以BD=DE,因为BF=CE,∠B=∠CED=90°,所以△BDF≌△EDC. (4分)
(2)AC=AB+BF. (5分)
理由:易得△ABD≌△AED,所以AB=AE,因为BF=CE,所以AC=AE+CE=AB+BF,
即AC=AB+BF. (8分)
14.解:(1)如图,过点N作NE∥AB,所以∠APN+∠PNE=180°,
因为∠APN+∠PNQ+∠CQN=360°,所以∠APN+∠PNE+∠ENQ+∠CQN=360°,
所以180°+∠ENQ+∠CQN=360°,所以∠ENQ+∠CQN=180°,
所以EN∥CD, (4分)
因为NE∥AB,所以AB∥CD. (5分)
(2)∠M=∠PNQ. (6分)
理由:因为AB∥CD∥NE,所以∠BPN=∠PNE,∠DQN=∠QNE,
所以∠BPN+∠DQN=∠PNQ,同理可得∠BPM+∠DQM=∠M,
因为PM,QM分别平分∠BPN,∠DQN,
所以∠BPN=2∠BPM,∠DQN=2∠DQD,所以∠BPN+∠DQN=2(∠BPM+∠DQM),
所以∠PNQ=2∠M,即∠M=∠PNQ. (12分)
15.解:(1)有. (1分)
如图,连接BC,在△ABC中,∠A+∠ABC+∠ACB=180°,在△OBC中,∠BOC+∠OBC+∠OCB=180°,所以∠A+∠ABC+∠ACB=∠BOC+∠OBC+∠OCB,所以∠A+∠ABC-∠OBC+∠ACB-∠OCB=∠BOC,所以∠BOC=∠A+∠ABO+∠ACO. (4分)
(2)如图,连接AD,由(1)可知∠F+∠2+∠3=130°,∠C+∠4+∠1=100°,所以∠F+∠2+∠3+∠C+∠4+∠1=230°,所以∠F+(∠1+∠2)+∠C+(∠3+∠4)=230°,
所以∠FAB+∠C+∠CDE+∠F=230°. (7分)
(3)EC∥BF∥DG. (8分)
理由:因为∠EOD+∠OBF=180°,∠EOD=∠BOC,所以∠BOC+∠OBF=180°,所以EC∥BF;
因为∠CDG=∠F,所以DG∥BF,所以EC∥BF∥DG. (10分)
(4)149.5° (14分)
提示:因为AB=AC,所以∠ABC=∠ACB=(180°-58°)=61°,又因为CE平分∠ACB,所以∠ECD=∠ECB=30.5°,又因为DG∥EC,所以∠CDG=∠DCE=30.5°,即∠ADG=149.5°.
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题5分,共30分)
1.如图,已知直线l上有一点A,直线m⊥n,则∠1与∠2的关系是 ( )
A.∠1与∠2相等 B.∠1与∠2互余
C.∠1与∠2互补 D.∠1与∠2是对顶角
2.如图,已知点D,B在线段AE上,若∠ABC=∠E,则下列结论正确的是 ( )
A.AC∥DF B.BD∥AC
C.BC∥EF D.DG∥AC
3.将一副三角板和一张对边平行的纸条按如图所示的方式摆放,两把三角板的一条直角边重合,则∠1与∠2之间的数量关系是 ( )
A.∠1+∠2=30° B.∠1+∠2=45°
C.∠1+∠2=60° D.2∠1+∠2=75°
4.在△ABC中,若∠A=2∠B,∠A=∠C+20°,则△ABC的形状是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.无法确定
5.若△ABC的三边长分别为a,b,c,则|a+b+c|+|a-b-c|的值为 ( )
A.a+2b B.2b+2c
C.2a+2c D.2b+c
6.如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E,连接CD,DM,BM,则下列结论正确的有 ( )
①∠CBD=∠CDB;②CM⊥BD;③∠CDB+∠A=90°.
A.①② B.①③ C.②③ D.①②③
二、填空题(每小题5分,共20分)
7.如图,已知点C是AE的中点,∠A=∠ECD,AB=CD,那么△ABC≌△CDE的根据是 .(填“SSS”“SAS”“ASA”或“AAS”)
8.如图所示,这是一个正五边形,它是一个轴对称图形,它有 条对称轴.
9.如图,在“4”字图中,BC与EF相交于点D,若图中有a对同位角,b对内错角,c对同旁内角,d对对顶角,则(a+b-c+d)3的值为 .
10.如图,已知AB∥CD,AE⊥EF,则∠A,∠C,∠F之间的数量关系是 .
三、解答题(本大题5小题,共50分)
11.(8分)如图,直线AB与EF相交于点O.
(1)若∠AOE=45°,∠AOF=3∠COF,试说明AB⊥CO;
(2)在(1)的条件下,找出所有与∠COF互余的角和互补的角.
12.(8分)如图,已知在Rt△ABC中,∠C=90°.
(1)尺规作图(保留作图痕迹,标明字母):
①作∠ACB的平分线CD,交AB于点D;
②延长BC到点E,使得CE=CA,连接AE.
(2)试判断CD与AE的位置关系,并说明理由.
13.(8分)如图,在Rt△ABC中,∠B=90°,AD是∠BAC的平分线,DE⊥AC于点E,点F是AB上一点,BF=CE.
(1)△BDF和△EDC全等吗 请说明理由.
(2)试猜想AC,AB,BF之间的数量关系,并说明理由.
14.(12分)如图,已知点P,Q分别在直线AB,CD上,∠APN+∠PNQ+∠CQN=360°.
(1)试说明AB∥CD;
(2)若PM,QM分别平分∠BPN,∠DQN,试探究∠M与∠N之间的数量关系,并说明理由.
15.(14分)阅读材料,完成后面的任务:
材料:如图1,在凹四边形ABOC中,试探究∠BOC与∠A,∠B,∠C之间的数量关系.小明发现并提供了如下方法:
解:∠BOC=∠A+∠B+∠C.如图2,连接AO并延长,因为∠1+∠B+∠AOB=180°,∠3+∠AOB=180°,所以∠3=∠1+∠B,同理∠4=∠2+∠C,所以∠3+∠4=∠1+∠2+∠B+∠C,所以∠BOC=∠BAC+∠B+∠C.
任务:(1)你有与小明不同的方法吗 请写出你的解答过程.
(2)如图3所示,根据图中标注的角的度数,请说明∠A+∠C+∠D+∠F=230°.
(3)如图4所示,在△ABC中,AB=AC,∠ABC,∠ACB的平分线BD,CE交于点O,∠EOD+∠OBF=180°,BF交AC的延长线于点F,∠CDG=∠F,DG交BC的延长线于点G,找出图中的平行线,并说明理由.
(4)在(3)的条件下,若∠A=58°,直接写出∠ADG的度数: .
参考答案
一、选择题
1 2 3 4 5 6
B C B A B D
1.B 【解析】因为∠1+∠2=180°-90°=90°,所以∠1与∠2互余.
2.C 【解析】因为∠ABC=∠E,所以BC∥EF.
3.B 【解析】如图,过点F作HF∥AB,因为AB∥CD,所以HF∥AB∥CD,所以∠1=∠EFH,∠2=∠GFH,所以∠1+∠2=∠EFG=45°.
4.A 【解析】设∠B=x,则∠A=2x,∠C=2x-20°,因为∠A+∠B+∠C=180°,所以2x+x+2x-20°=180°,解得x=40°,所以∠A=80°,∠B=40°,∠C=60°,所以△ABC是锐角三角形.
5.B 【解析】原式=a+b+c+b+c-a=2b+2c.
6.D 【解析】①由作图可知,CB=CD,所以△CBD是等腰三角形,所以∠CBD=∠CDB,正确;②由作图可知,DM=BM,CB=CD,因为CM=CM,所以△CBM≌△CDM,所以∠DCM=∠BCM,所以CM⊥BD,正确;③因为AB=AC,所以∠CBD=∠ACB,因为∠CBD+∠ACB+∠A=180°,所以2∠CBD+∠A=180°,所以∠CBD+∠A=90°,因为∠CBD=∠CDB,所以∠CDB+∠A=90°,正确.
二、填空题
7.SAS
8.5
9.27 【解析】由图可知a=1,b=1,c=1,d=2,所以(a+b-c+d)3=(1+1-1+2)3=27.
10.∠A+∠C+∠EFC=270° 【解析】 如图,过点F作FG∥AB,因为AB∥CD,所以FG∥AB∥CD,同理,过点E作EH∥AB,则EH∥AB∥CD,所以∠A=∠AEH,∠EFG=∠FEH,即∠A+∠EFG=∠AEF=90°,因为∠GFC+∠C=180°,所以∠A+∠EFC+∠C=90°+180°=270°.
三、解答题
11.解:(1)因为∠AOE=45°,所以∠BOF=∠AOE=45°,所以∠AOF=180°-45°=135°,因为∠AOF=3∠COF,所以3∠COF=135°,所以∠COF=45°,所以∠COB=90°,
所以AB⊥CO. (4分)
(2)与∠COF互余的角:∠BOF,∠AOE;与∠COF互补的角:∠COE. (8分)
12.解:(1)如图所示: (4分)
(2)因为AC=CE,AC⊥CE,
所以△ACE是等腰直角三角形,
所以∠CAE=45°, (6分)
因为CD平分∠ACB,所以∠ACD=45°,
所以∠ACD=∠CAE,所以CD∥AE. (8分)
技巧点拨 本题属于作图与说理为一体的几何问题,猜想结论性问题是中考的一大亮点问题,在第(2)小问中,只要作图准确,就可得出正确的结论.两直线的位置关系主要有两种:一是平行,二是垂直.要说明两直线平行,只需说明同位角相等或内错角相等或同旁内角互补.
13.解:(1)△BDF≌△EDC. (1分)
理由:因为∠B=90°,AD是∠BAC的平分线,DE⊥AC,
所以BD=DE,因为BF=CE,∠B=∠CED=90°,所以△BDF≌△EDC. (4分)
(2)AC=AB+BF. (5分)
理由:易得△ABD≌△AED,所以AB=AE,因为BF=CE,所以AC=AE+CE=AB+BF,
即AC=AB+BF. (8分)
14.解:(1)如图,过点N作NE∥AB,所以∠APN+∠PNE=180°,
因为∠APN+∠PNQ+∠CQN=360°,所以∠APN+∠PNE+∠ENQ+∠CQN=360°,
所以180°+∠ENQ+∠CQN=360°,所以∠ENQ+∠CQN=180°,
所以EN∥CD, (4分)
因为NE∥AB,所以AB∥CD. (5分)
(2)∠M=∠PNQ. (6分)
理由:因为AB∥CD∥NE,所以∠BPN=∠PNE,∠DQN=∠QNE,
所以∠BPN+∠DQN=∠PNQ,同理可得∠BPM+∠DQM=∠M,
因为PM,QM分别平分∠BPN,∠DQN,
所以∠BPN=2∠BPM,∠DQN=2∠DQD,所以∠BPN+∠DQN=2(∠BPM+∠DQM),
所以∠PNQ=2∠M,即∠M=∠PNQ. (12分)
15.解:(1)有. (1分)
如图,连接BC,在△ABC中,∠A+∠ABC+∠ACB=180°,在△OBC中,∠BOC+∠OBC+∠OCB=180°,所以∠A+∠ABC+∠ACB=∠BOC+∠OBC+∠OCB,所以∠A+∠ABC-∠OBC+∠ACB-∠OCB=∠BOC,所以∠BOC=∠A+∠ABO+∠ACO. (4分)
(2)如图,连接AD,由(1)可知∠F+∠2+∠3=130°,∠C+∠4+∠1=100°,所以∠F+∠2+∠3+∠C+∠4+∠1=230°,所以∠F+(∠1+∠2)+∠C+(∠3+∠4)=230°,
所以∠FAB+∠C+∠CDE+∠F=230°. (7分)
(3)EC∥BF∥DG. (8分)
理由:因为∠EOD+∠OBF=180°,∠EOD=∠BOC,所以∠BOC+∠OBF=180°,所以EC∥BF;
因为∠CDG=∠F,所以DG∥BF,所以EC∥BF∥DG. (10分)
(4)149.5° (14分)
提示:因为AB=AC,所以∠ABC=∠ACB=(180°-58°)=61°,又因为CE平分∠ACB,所以∠ECD=∠ECB=30.5°,又因为DG∥EC,所以∠CDG=∠DCE=30.5°,即∠ADG=149.5°.
同课章节目录
