期中检测卷(含答案)---2024-2025学年六年级数学下册真题重组检测卷(人教版)
文档属性
| 名称 | 期中检测卷(含答案)---2024-2025学年六年级数学下册真题重组检测卷(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 178.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 20:56:17 | ||
图片预览




文档简介
保密★启用前
2024-2025学年六年级下册期中真题重组检测卷(人教版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.(2024六下·瑞金期中)下面几组相关联的量中,成正比例关系的是( )。
A.总价一定,单价和数量。
B.正方体的底面积一定,体积和高。
C.圆的周长和半径。
D.儿童的年龄和身高。
2.(2024六下·南昌期中)一个长方形操场长250m,宽200m,选用比例尺( )画出的平面图最大。
A.1:500 B.1:5000 C.1:50000 D.1:1000
3.(2024六下·黄石期中)如果x=5y,x和y成( )比例关系。
A.正比例 B.反比例 C.不成比例 D.无法确定
4.(2024六下·江门期中)一个圆柱体的底面半径是3厘米,高是18.84厘米,它的侧面展开图是( )。
A.正方形
B.长方形
C.两个圆形和一个长方形组成
5.(2024六下·玉田期中)下面说法错误的是( )
A.0是最小的整数。
B.圆锥的侧面展开后是一个扇形。
C.一个保温杯最多装水450毫升,说明它的容积是450毫升。
6.(2019六下·金寨期中)一架客机从北京飞往上海,飞行速度和所用时间( )。
A.成正比例 B.成反比例 C.不成比例
7.(2021六下·阳东期中)周长相等的正方形、长方形和圆形,( )的面积最大。
A.正方形 B.长方形 C.圆 D.无法确定
8.(2023六下·宝安期中)下面选项中,哪个选项两个比能组成比例 ( )。
A.和6:18 B.:18和:6
C.6:和18:3 D.:6和:18
9.(2021六下·大冶期中)下面的比中能与3:8组成比例的是( )。
A.3.5:6 B.6:1.54 C.1.5:4 D.3:2
10.(2024六下·洞头期中)一个圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.(2022六下·泾阳期中)如图 ,一面小旗被扶起插好,这面小旗绕点O顺时针方向旋转了90°。( )
12.(2022六下·南召期中)一个圆柱与圆锥等底等高,圆柱的体积比圆锥多18m3,圆锥的体积是9m3。( )
13.(2022六下·南召期中)比例5:3=15:9的内项3增加6,要使比例成立,外项9应该增加6。( )
14.(2019六下·端州期中)圆柱体的表面积=底面积×2+底面积×高.( )
15.(2024六下·武江期中)3,6,9,10这四个数可以组成比例。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.(2023六下·宝安期中)一种精密零件长是6毫米,画在图纸上长是12厘米,这份图纸的比例尺是 。
17.(2022-2023学年六下·老河口期中)甲、乙两个商场都推出了“五一”促销活动。甲商场8折优惠,乙商场“满100元减20元”,陈老师要买的榨汁机在两店的标价均是320元,去 商场更优惠。
18.(2024六下·平川期中) 比80多25%,60比 少25%, 的25%是15。
19.(2024六下·平川期中)甲、乙两地相距100km,在一幅地图上量得两地的距离是10cm,这幅地图的比例尺是 如果在这幅地图上量得丙、丁两地的距离是15cm,那么丙、丁两地的实际距离是 km.
20.(2024六下·平川期中)如果把一个圆柱的高截短3cm,表面积就减少了这个圆柱的底面积是 cm2,如果这个圆柱高5cm,体积是
21.(2023六下·宿迁期中)在比例尺是1:5000000的地图上,量得上海到杭州的距离是3.4厘米,上海到杭州的实际距离是 千米。
22.(2024六下·万载期中)中国国旗是国家的象征和标志,我们都应当尊重和爱护。一号国旗长为288厘米,宽为192厘米,由此可见我国国旗的长宽比为 ,学校需要做一面长为2.4米的国旗,这面国旗的面积是 平方米。
23.(2022六下·宿迁期中)在一幅地图上,用2.5厘米的长度表示实际距离20千米,这幅地图的比例尺是 。
24.(2024六下·蓬江期中)一个比例,其中两个内项的积是最小的质数,已知一个外项是,则另一个外项是 。
25.(2024六下·江门期中)一件衣服打八五折出售,也就是便宜了 %,便宜了30元,衣服原价是 元。
阅卷人 四、计算题(23分)
得分
26.(2024六下·平川期中)直接写出得数。
=
27.(2024六下·苍溪期中)计算下面圆柱的表面积及圆锥的体积。(单位:厘米)
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
28.(2023六下·恩施期中)某一人造地球卫星在空中绕地球运行3周需要7.5小时。照这样计算运行14周需要多少小时?(用比例知识解答)
29.(2024六下·平川期中).一个圆柱形水杯,底面半径为5厘米,杯中有一个底面积是30平方厘米的圆锥形铁块,完全淹没在水中,如果从水中取出这块铁块,水面下降2厘米,这个圆锥形铁块的体积是多少立方厘米.
30.(2024六下·平川期中)把一个底面半径4dm,高6dm的圆柱形铁块熔铸成一个底面半径是3dm的圆锥,这个圆锥的高是多少分米?
31.(2024六下·江门期中)甲、乙两个仓库存有同样质量的货物,如果从甲仓运出60吨货物到乙仓那么两个仓库存货质量的比是 2:3,两个仓库原来各存货多少吨?
32.(2024六下·江门期中)小明送妈妈一只茶杯。底面直径8厘米,高20 米。
(1)这只茶杯占据来面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带很漂亮,那是小明怕烫伤妈妈的手特意贴上的,这条装饰带宽5厘米,装饰带的面积有多少平方厘米?(接头处忽略不计)
(3)这只茶杯能装多少毫升水?
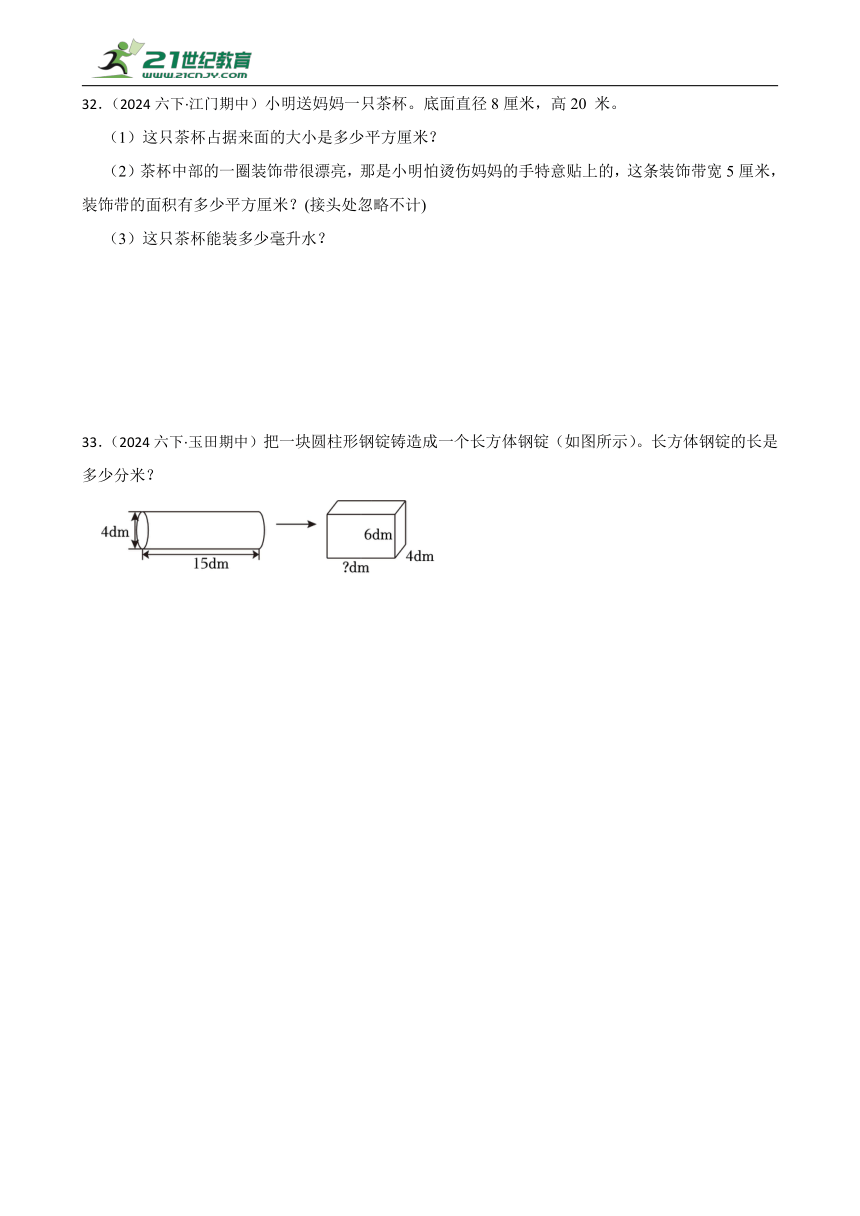
33.(2024六下·玉田期中)把一块圆柱形钢锭铸造成一个长方体钢锭(如图所示)。长方体钢锭的长是多少分米?
答案解析部分
1.C
A.因为数量×单价=总价(一定),两个数的乘积一定,所以单价和数量成反比例;
B.正方体的底面积一定,说明高和体积是个定值,不存在变量,所以高和体积不成比例;
C.圆的周长:半径=2,两个数的比值一定,所以圆的周长和半径成正比例;
D.儿童的年龄和身高不成比例。
故答案为:C。
正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量;
反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。
2.A
解:250米=25000厘米,200米=20000厘米;
A:25000×=50(厘米),20000×=40(厘米),50×40=2000(平方厘米);
。
故答案为:A。
图上距离=比例尺×实际距离;据此求出长方形操场的图上长和宽,然后根据“长×宽”求出操场的图上面积,比较即可。
3.A
解:由x=5y可得x÷y=5,x和y成正比例关系。
故答案为:A。
正比例的判断方法:相关联,能变化,商一定。
4.A
解:2×3.14×3=18.84(厘米)
底面周长和高相等,它的侧面展开图是正方形。
故答案为:A。
当底面周长和高相等时,圆柱的侧面展开图是一个正方形;当底面周长和高不相等时,圆柱的侧面展开图是一个长方形;当沿着侧面斜着剪开时,圆柱的侧面是一个平行四边形。
5.A
解:A:0不是最小的整数,因为还有负整数,这些负整数都比0小,原题说法错误;
B:圆锥的侧面展开后是一个扇形,原题说法正确;
C:一个保温杯最多装水450毫升,说明它的容积是450毫升,原题说法正确。
故答案为:A。
正整数、0、负整数都是整数,据此解答。
6.B
因为飞行速度×所用时间=从北京到上海的路程,从北京到上海的路程是一定的,飞机飞行速度与所用时间成反比例。
故答案为:B。
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
7.C
周长相等的正方形、长方形和圆,圆的面积最大.
故答案为:C.
此题主要考查了图形的周长和面积的比较,周长相等的正方形、长方形和圆的面积:圆的面积>正方形的面积>长方形的面积,据此解答.
8.B
解:选项A:÷=3,6÷18=,不能组成比例;
选项B:÷18=,÷6=,能够组成比例;
选项C:6÷=54,18÷3=6,所以不能组成比例;
选项D:÷6=,÷18=,所以不能组成比例。
故答案为:B。
比值相等的两个比可以组成比例,比值=比的前项÷比的后项,据此解答。
9.C
解:能组成比例的是:
3:8=1.5:4
故答案为:C。
比例的基本性质,在比例里,两个内项积等于两个外项积。
10.D
解:3×3×3=27。
故答案为:D。
圆柱的体积=π×半径2×高,圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的3×3×3=27倍。
11.错误
解:这面小旗绕点O逆时针方向旋转了90°,原题说法错误。
故答案为:错误。
旋转后图形的位置改变,转动的中心点、形状、大小不变。
12.正确
解:圆锥的体积:18÷2=9( m3 ),
圆柱的体积是:9×3=27( m3 )
故答案为:正确。
等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱的体积比圆锥的体积多2倍,由此即可解答。
13.错误
解:3+6=9;
9×15÷5
=135÷5
=27
27-9=16,所以外项应该增加16。
故答案为:错误。
内项3+6=9,根据比例的基本性质,两内项的积等于两外项的积,所以外项等于9×15÷5=27,27-9=16,据此解答。
14.错误
解:圆柱体的表面积=底面积×2+底面周长×高。原题说法错误。
故答案为:错误。
圆柱的表面积=底面积×2+侧面积,圆柱的侧面积=底面周长×高,所以圆柱体的表面积=底面积×2+底面周长×高。
15.错误
解:3,6,9,10这四个数找不到比值相等的两个比,所以组不成比例。原题说法错误。
故答案为:错误。
比值相等的两个比,可以组成比例。
16.20:1
解:12厘米=120毫米
120:6=20:1
故答案为:20:1。
比例尺=图上距离:实际距离,据此解答。
17.甲
解:甲商场:320×80%=256(元);
乙商场:320÷100=3……20(元),320-20×3=320-60=260(元)。
256<260,所以去甲商场更优惠。
故答案为:甲。
在甲商场花的钱数=榨汁机的标价×在甲商场打的折扣数;
在乙商场花的钱数=榨汁机的标价-榨汁机的标价里面有100圆的个数×满100元减去的钱数。
最后把两个商场花的钱数进行比较即可。
18.100;80;60
解:80×(1+25%)
=80×1.25
=100
60÷(1-25%)
=60÷75%
=80
15÷25%=60
故答案为:100;80;60。
把80看成单位“1”,要求的数是单位“1”的(1+25%),用乘法可以求出要求的数;
把要求的数看成单位“1”,60是单位“1”的(1-25%),用除法求出单位“1”的量;
把要求的数看成单位“1”,15是单位“1”的25%,用除法求出单位“1”的量。
19.1:1000000;150
解:10cm:100km= 10cm:10000000cm=(10÷10): (10000000÷10)=1:1000000
15÷= 15×1000000=15000000 (cm)=150 (km)
所以这幅地图的比例尺是1:1000000;丙、丁两地的实际距离是150km。
故答案为:1:1000000;150。
图上距离:实际距离=比例尺,据此写出图上距离与实际距离的比,化简得到比例尺;根据实际距离=图上距离÷比例尺,进行换算即可。
20.78.5;392.5
解:底面周长:94.2÷3=31.4(cm)
底面半径:31.4÷3.14÷2=5(cm)
底面积:3.14×52
=3.14×25
=78.5(cm2)
体积:78.5×5=392.5(cm2)
故答案为:78.5;392.5。
减少的表面积是侧面积,减少的表面积÷截短的高=底面周长,底面半径=底面周长÷圆周率÷2,底面积=圆周率×半径的平方,圆柱体积=底面积x高,据此列式计算。
21.170
解:3.4÷=17000000(厘米),17000000厘米=170千米。
故答案为:170。
用图上距离除以比例尺即可求出实际距离,把实际距离换算成千米即可,1千米=100000厘米。
22.3:2;3.84
解:288:192=(288÷96):(192÷96)=3:2;
2.4÷3×2×2.4
=1.6×2.4
=3.84(平方米)。
故答案为:3:2;3.84。
我国国旗的长、宽比=长:宽,依据比的基本性质化简比;
这面国旗的面积=长×宽;其中,宽=长÷长占的份数×宽占的份数。
23.1:800000
解:20千米=2000000厘米,比例尺是2.5:2000000=1:800000。
故答案为:1:800000。
先把实际距离换算成厘米,然后写出图上距离与实际距离的比并化成前项是1的比即可。
24.4
解:2÷=4。
故答案为:4。
最小的质数是2, 比例的基本性质:在比例里,两个内项积等于两个外项积,另一个外项=两个内项积÷其中一个外项。
25.15;200
解:1-85%=15%,30÷15%=200(元)。
故答案为:15;200。
根据题意可知打八五折即现价是原价的85%,把衣服原价看作单位“1”,1-折扣=便宜的钱占原价的百分比,便宜的钱÷便宜的钱占原价的百分比=衣服原价。
26.
8.99 1 4.9
0.16 5 =28.26
小数加减法的计算法则: 计算小数加、 减法,先把各数的小数点对齐(也就是把相同数位上的数对齐)。 再按照整数加、 减法的法则进行计算。
小数乘分数,先把小数化成分数,然后用分数乘法的计算法则:分数的分子与分子相乘,分母与分母相乘,能约分的要先约分。
分数除以分数,等于这个数乘除数的倒数。
小数乘整数,先按照( 整数 )乘法的计算方法算出积,再看(因数)中一共有几位( 小数),就从积的( 右边)起数出几位,点上(小数点)。
27.解:圆柱表面积:
3.14×(6÷2)2×2+3.14×6×9
=3.14×9×2+18.84×9
=56.52+169.56
=226.08(平方厘米)
圆锥体积:
×3.14×32×5
=×28.26×5
=9.42×5
=47.1(立方厘米)
答:圆柱的表面积是226.085平方厘米;圆锥的体积是47.1立方厘米。
圆柱表面积=底面积×2+侧面积=π×半径2×2+π×直径×高;圆锥体积=×π×半径2×高;据此代入数值计算即可。
28.解:设运行14周需要x小时。
7.5:3=x:14
3x=7.5×14
3x=105
x=105÷3
x=35
答:需要35小时。
依据运行3周需要的时间:3=运行14周需要的时间:需要的周数,列比例,解比例。
29.解: 3.14×52×2
=3.14×25×2
=157(立方厘米)
答:这块铁块的体积是157立方厘米。
“铁块的体积=水面下降后减少的水那一部分的体积”,即求这块铁块的体积是多少,也就是求半径是5厘米,高是2厘米的圆柱形容器里水的体积。
30.解:3.14×42×6
=3.14×16×6
=301.44(立方分米)
(301.44×3)÷(3.14×32)
=904.32÷28.26
=32(分米)
答: 这个圆锥的高是32分米 。
根据题意可知,圆柱与圆锥的体积是相等的,根据圆柱的体积V=Πr2h,求出圆柱的体积,也就是圆锥的体积,再乘3除以圆锥的底面积即可。
31.解:设两个仓库原来各存货x吨。
(x-60):(x+60)=2:3
2x+120=3x-180
3x-2x=180+120
x=300
答:两个仓库原来各存货300吨。
根据题意可得:(甲仓库原有存货-甲仓库运出的货物):(乙仓库原有存货+甲仓库运出的货物)=2:3,且甲仓库原有存货=乙仓库原有存货,据此关系式设两个仓库原来各存货x吨,列比例即可解答。
32.(1)解:8÷2=4(厘米)
3.14×42=50.24(平方厘米)
答:这只茶杯占据桌面的大小是50.24平方厘米。
(2)解:3.14×8×5
=25.12×5
=125.6(平方厘米)
答:装饰带的面积有125.6平方厘米。
(3)解:50.24×20=1004.8(立方厘米)
1004.8立方厘米=1004.8(毫升)
答:这只茶杯能装1004.8毫升水。
(1)根据题意可知求占据桌面的大小即求茶杯的底面积:直径÷2=半径,底面积=圆周率×半径的平方;
(2)根据题意可知求装饰带的面积即求高5厘米、直径8厘米的圆柱的侧面积:侧面积=圆周率×直径×高;
(3)圆柱的体积=底面积×高,最后将体积单位转化成容积单位:1立方厘米=1毫升。
33.解:4÷2=2(分米)
2×2×3.14×15
=12.56×15
=188.4(立方分米)
188.4÷6÷4
=31.4÷4
=7.85(分米)
答:长方体钢锭的长是7.85分米。
本题属于等积变形,圆柱的体积=长方体的体积;π×底面半径的平方×高=圆柱的体积,圆柱的体积÷长方体的高÷长方体的宽=长方体的长。
2024-2025学年六年级下册期中真题重组检测卷(人教版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.(2024六下·瑞金期中)下面几组相关联的量中,成正比例关系的是( )。
A.总价一定,单价和数量。
B.正方体的底面积一定,体积和高。
C.圆的周长和半径。
D.儿童的年龄和身高。
2.(2024六下·南昌期中)一个长方形操场长250m,宽200m,选用比例尺( )画出的平面图最大。
A.1:500 B.1:5000 C.1:50000 D.1:1000
3.(2024六下·黄石期中)如果x=5y,x和y成( )比例关系。
A.正比例 B.反比例 C.不成比例 D.无法确定
4.(2024六下·江门期中)一个圆柱体的底面半径是3厘米,高是18.84厘米,它的侧面展开图是( )。
A.正方形
B.长方形
C.两个圆形和一个长方形组成
5.(2024六下·玉田期中)下面说法错误的是( )
A.0是最小的整数。
B.圆锥的侧面展开后是一个扇形。
C.一个保温杯最多装水450毫升,说明它的容积是450毫升。
6.(2019六下·金寨期中)一架客机从北京飞往上海,飞行速度和所用时间( )。
A.成正比例 B.成反比例 C.不成比例
7.(2021六下·阳东期中)周长相等的正方形、长方形和圆形,( )的面积最大。
A.正方形 B.长方形 C.圆 D.无法确定
8.(2023六下·宝安期中)下面选项中,哪个选项两个比能组成比例 ( )。
A.和6:18 B.:18和:6
C.6:和18:3 D.:6和:18
9.(2021六下·大冶期中)下面的比中能与3:8组成比例的是( )。
A.3.5:6 B.6:1.54 C.1.5:4 D.3:2
10.(2024六下·洞头期中)一个圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.(2022六下·泾阳期中)如图 ,一面小旗被扶起插好,这面小旗绕点O顺时针方向旋转了90°。( )
12.(2022六下·南召期中)一个圆柱与圆锥等底等高,圆柱的体积比圆锥多18m3,圆锥的体积是9m3。( )
13.(2022六下·南召期中)比例5:3=15:9的内项3增加6,要使比例成立,外项9应该增加6。( )
14.(2019六下·端州期中)圆柱体的表面积=底面积×2+底面积×高.( )
15.(2024六下·武江期中)3,6,9,10这四个数可以组成比例。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.(2023六下·宝安期中)一种精密零件长是6毫米,画在图纸上长是12厘米,这份图纸的比例尺是 。
17.(2022-2023学年六下·老河口期中)甲、乙两个商场都推出了“五一”促销活动。甲商场8折优惠,乙商场“满100元减20元”,陈老师要买的榨汁机在两店的标价均是320元,去 商场更优惠。
18.(2024六下·平川期中) 比80多25%,60比 少25%, 的25%是15。
19.(2024六下·平川期中)甲、乙两地相距100km,在一幅地图上量得两地的距离是10cm,这幅地图的比例尺是 如果在这幅地图上量得丙、丁两地的距离是15cm,那么丙、丁两地的实际距离是 km.
20.(2024六下·平川期中)如果把一个圆柱的高截短3cm,表面积就减少了这个圆柱的底面积是 cm2,如果这个圆柱高5cm,体积是
21.(2023六下·宿迁期中)在比例尺是1:5000000的地图上,量得上海到杭州的距离是3.4厘米,上海到杭州的实际距离是 千米。
22.(2024六下·万载期中)中国国旗是国家的象征和标志,我们都应当尊重和爱护。一号国旗长为288厘米,宽为192厘米,由此可见我国国旗的长宽比为 ,学校需要做一面长为2.4米的国旗,这面国旗的面积是 平方米。
23.(2022六下·宿迁期中)在一幅地图上,用2.5厘米的长度表示实际距离20千米,这幅地图的比例尺是 。
24.(2024六下·蓬江期中)一个比例,其中两个内项的积是最小的质数,已知一个外项是,则另一个外项是 。
25.(2024六下·江门期中)一件衣服打八五折出售,也就是便宜了 %,便宜了30元,衣服原价是 元。
阅卷人 四、计算题(23分)
得分
26.(2024六下·平川期中)直接写出得数。
=
27.(2024六下·苍溪期中)计算下面圆柱的表面积及圆锥的体积。(单位:厘米)
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
28.(2023六下·恩施期中)某一人造地球卫星在空中绕地球运行3周需要7.5小时。照这样计算运行14周需要多少小时?(用比例知识解答)
29.(2024六下·平川期中).一个圆柱形水杯,底面半径为5厘米,杯中有一个底面积是30平方厘米的圆锥形铁块,完全淹没在水中,如果从水中取出这块铁块,水面下降2厘米,这个圆锥形铁块的体积是多少立方厘米.
30.(2024六下·平川期中)把一个底面半径4dm,高6dm的圆柱形铁块熔铸成一个底面半径是3dm的圆锥,这个圆锥的高是多少分米?
31.(2024六下·江门期中)甲、乙两个仓库存有同样质量的货物,如果从甲仓运出60吨货物到乙仓那么两个仓库存货质量的比是 2:3,两个仓库原来各存货多少吨?
32.(2024六下·江门期中)小明送妈妈一只茶杯。底面直径8厘米,高20 米。
(1)这只茶杯占据来面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带很漂亮,那是小明怕烫伤妈妈的手特意贴上的,这条装饰带宽5厘米,装饰带的面积有多少平方厘米?(接头处忽略不计)
(3)这只茶杯能装多少毫升水?
33.(2024六下·玉田期中)把一块圆柱形钢锭铸造成一个长方体钢锭(如图所示)。长方体钢锭的长是多少分米?
答案解析部分
1.C
A.因为数量×单价=总价(一定),两个数的乘积一定,所以单价和数量成反比例;
B.正方体的底面积一定,说明高和体积是个定值,不存在变量,所以高和体积不成比例;
C.圆的周长:半径=2,两个数的比值一定,所以圆的周长和半径成正比例;
D.儿童的年龄和身高不成比例。
故答案为:C。
正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量;
反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。
2.A
解:250米=25000厘米,200米=20000厘米;
A:25000×=50(厘米),20000×=40(厘米),50×40=2000(平方厘米);
。
故答案为:A。
图上距离=比例尺×实际距离;据此求出长方形操场的图上长和宽,然后根据“长×宽”求出操场的图上面积,比较即可。
3.A
解:由x=5y可得x÷y=5,x和y成正比例关系。
故答案为:A。
正比例的判断方法:相关联,能变化,商一定。
4.A
解:2×3.14×3=18.84(厘米)
底面周长和高相等,它的侧面展开图是正方形。
故答案为:A。
当底面周长和高相等时,圆柱的侧面展开图是一个正方形;当底面周长和高不相等时,圆柱的侧面展开图是一个长方形;当沿着侧面斜着剪开时,圆柱的侧面是一个平行四边形。
5.A
解:A:0不是最小的整数,因为还有负整数,这些负整数都比0小,原题说法错误;
B:圆锥的侧面展开后是一个扇形,原题说法正确;
C:一个保温杯最多装水450毫升,说明它的容积是450毫升,原题说法正确。
故答案为:A。
正整数、0、负整数都是整数,据此解答。
6.B
因为飞行速度×所用时间=从北京到上海的路程,从北京到上海的路程是一定的,飞机飞行速度与所用时间成反比例。
故答案为:B。
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
7.C
周长相等的正方形、长方形和圆,圆的面积最大.
故答案为:C.
此题主要考查了图形的周长和面积的比较,周长相等的正方形、长方形和圆的面积:圆的面积>正方形的面积>长方形的面积,据此解答.
8.B
解:选项A:÷=3,6÷18=,不能组成比例;
选项B:÷18=,÷6=,能够组成比例;
选项C:6÷=54,18÷3=6,所以不能组成比例;
选项D:÷6=,÷18=,所以不能组成比例。
故答案为:B。
比值相等的两个比可以组成比例,比值=比的前项÷比的后项,据此解答。
9.C
解:能组成比例的是:
3:8=1.5:4
故答案为:C。
比例的基本性质,在比例里,两个内项积等于两个外项积。
10.D
解:3×3×3=27。
故答案为:D。
圆柱的体积=π×半径2×高,圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的3×3×3=27倍。
11.错误
解:这面小旗绕点O逆时针方向旋转了90°,原题说法错误。
故答案为:错误。
旋转后图形的位置改变,转动的中心点、形状、大小不变。
12.正确
解:圆锥的体积:18÷2=9( m3 ),
圆柱的体积是:9×3=27( m3 )
故答案为:正确。
等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱的体积比圆锥的体积多2倍,由此即可解答。
13.错误
解:3+6=9;
9×15÷5
=135÷5
=27
27-9=16,所以外项应该增加16。
故答案为:错误。
内项3+6=9,根据比例的基本性质,两内项的积等于两外项的积,所以外项等于9×15÷5=27,27-9=16,据此解答。
14.错误
解:圆柱体的表面积=底面积×2+底面周长×高。原题说法错误。
故答案为:错误。
圆柱的表面积=底面积×2+侧面积,圆柱的侧面积=底面周长×高,所以圆柱体的表面积=底面积×2+底面周长×高。
15.错误
解:3,6,9,10这四个数找不到比值相等的两个比,所以组不成比例。原题说法错误。
故答案为:错误。
比值相等的两个比,可以组成比例。
16.20:1
解:12厘米=120毫米
120:6=20:1
故答案为:20:1。
比例尺=图上距离:实际距离,据此解答。
17.甲
解:甲商场:320×80%=256(元);
乙商场:320÷100=3……20(元),320-20×3=320-60=260(元)。
256<260,所以去甲商场更优惠。
故答案为:甲。
在甲商场花的钱数=榨汁机的标价×在甲商场打的折扣数;
在乙商场花的钱数=榨汁机的标价-榨汁机的标价里面有100圆的个数×满100元减去的钱数。
最后把两个商场花的钱数进行比较即可。
18.100;80;60
解:80×(1+25%)
=80×1.25
=100
60÷(1-25%)
=60÷75%
=80
15÷25%=60
故答案为:100;80;60。
把80看成单位“1”,要求的数是单位“1”的(1+25%),用乘法可以求出要求的数;
把要求的数看成单位“1”,60是单位“1”的(1-25%),用除法求出单位“1”的量;
把要求的数看成单位“1”,15是单位“1”的25%,用除法求出单位“1”的量。
19.1:1000000;150
解:10cm:100km= 10cm:10000000cm=(10÷10): (10000000÷10)=1:1000000
15÷= 15×1000000=15000000 (cm)=150 (km)
所以这幅地图的比例尺是1:1000000;丙、丁两地的实际距离是150km。
故答案为:1:1000000;150。
图上距离:实际距离=比例尺,据此写出图上距离与实际距离的比,化简得到比例尺;根据实际距离=图上距离÷比例尺,进行换算即可。
20.78.5;392.5
解:底面周长:94.2÷3=31.4(cm)
底面半径:31.4÷3.14÷2=5(cm)
底面积:3.14×52
=3.14×25
=78.5(cm2)
体积:78.5×5=392.5(cm2)
故答案为:78.5;392.5。
减少的表面积是侧面积,减少的表面积÷截短的高=底面周长,底面半径=底面周长÷圆周率÷2,底面积=圆周率×半径的平方,圆柱体积=底面积x高,据此列式计算。
21.170
解:3.4÷=17000000(厘米),17000000厘米=170千米。
故答案为:170。
用图上距离除以比例尺即可求出实际距离,把实际距离换算成千米即可,1千米=100000厘米。
22.3:2;3.84
解:288:192=(288÷96):(192÷96)=3:2;
2.4÷3×2×2.4
=1.6×2.4
=3.84(平方米)。
故答案为:3:2;3.84。
我国国旗的长、宽比=长:宽,依据比的基本性质化简比;
这面国旗的面积=长×宽;其中,宽=长÷长占的份数×宽占的份数。
23.1:800000
解:20千米=2000000厘米,比例尺是2.5:2000000=1:800000。
故答案为:1:800000。
先把实际距离换算成厘米,然后写出图上距离与实际距离的比并化成前项是1的比即可。
24.4
解:2÷=4。
故答案为:4。
最小的质数是2, 比例的基本性质:在比例里,两个内项积等于两个外项积,另一个外项=两个内项积÷其中一个外项。
25.15;200
解:1-85%=15%,30÷15%=200(元)。
故答案为:15;200。
根据题意可知打八五折即现价是原价的85%,把衣服原价看作单位“1”,1-折扣=便宜的钱占原价的百分比,便宜的钱÷便宜的钱占原价的百分比=衣服原价。
26.
8.99 1 4.9
0.16 5 =28.26
小数加减法的计算法则: 计算小数加、 减法,先把各数的小数点对齐(也就是把相同数位上的数对齐)。 再按照整数加、 减法的法则进行计算。
小数乘分数,先把小数化成分数,然后用分数乘法的计算法则:分数的分子与分子相乘,分母与分母相乘,能约分的要先约分。
分数除以分数,等于这个数乘除数的倒数。
小数乘整数,先按照( 整数 )乘法的计算方法算出积,再看(因数)中一共有几位( 小数),就从积的( 右边)起数出几位,点上(小数点)。
27.解:圆柱表面积:
3.14×(6÷2)2×2+3.14×6×9
=3.14×9×2+18.84×9
=56.52+169.56
=226.08(平方厘米)
圆锥体积:
×3.14×32×5
=×28.26×5
=9.42×5
=47.1(立方厘米)
答:圆柱的表面积是226.085平方厘米;圆锥的体积是47.1立方厘米。
圆柱表面积=底面积×2+侧面积=π×半径2×2+π×直径×高;圆锥体积=×π×半径2×高;据此代入数值计算即可。
28.解:设运行14周需要x小时。
7.5:3=x:14
3x=7.5×14
3x=105
x=105÷3
x=35
答:需要35小时。
依据运行3周需要的时间:3=运行14周需要的时间:需要的周数,列比例,解比例。
29.解: 3.14×52×2
=3.14×25×2
=157(立方厘米)
答:这块铁块的体积是157立方厘米。
“铁块的体积=水面下降后减少的水那一部分的体积”,即求这块铁块的体积是多少,也就是求半径是5厘米,高是2厘米的圆柱形容器里水的体积。
30.解:3.14×42×6
=3.14×16×6
=301.44(立方分米)
(301.44×3)÷(3.14×32)
=904.32÷28.26
=32(分米)
答: 这个圆锥的高是32分米 。
根据题意可知,圆柱与圆锥的体积是相等的,根据圆柱的体积V=Πr2h,求出圆柱的体积,也就是圆锥的体积,再乘3除以圆锥的底面积即可。
31.解:设两个仓库原来各存货x吨。
(x-60):(x+60)=2:3
2x+120=3x-180
3x-2x=180+120
x=300
答:两个仓库原来各存货300吨。
根据题意可得:(甲仓库原有存货-甲仓库运出的货物):(乙仓库原有存货+甲仓库运出的货物)=2:3,且甲仓库原有存货=乙仓库原有存货,据此关系式设两个仓库原来各存货x吨,列比例即可解答。
32.(1)解:8÷2=4(厘米)
3.14×42=50.24(平方厘米)
答:这只茶杯占据桌面的大小是50.24平方厘米。
(2)解:3.14×8×5
=25.12×5
=125.6(平方厘米)
答:装饰带的面积有125.6平方厘米。
(3)解:50.24×20=1004.8(立方厘米)
1004.8立方厘米=1004.8(毫升)
答:这只茶杯能装1004.8毫升水。
(1)根据题意可知求占据桌面的大小即求茶杯的底面积:直径÷2=半径,底面积=圆周率×半径的平方;
(2)根据题意可知求装饰带的面积即求高5厘米、直径8厘米的圆柱的侧面积:侧面积=圆周率×直径×高;
(3)圆柱的体积=底面积×高,最后将体积单位转化成容积单位:1立方厘米=1毫升。
33.解:4÷2=2(分米)
2×2×3.14×15
=12.56×15
=188.4(立方分米)
188.4÷6÷4
=31.4÷4
=7.85(分米)
答:长方体钢锭的长是7.85分米。
本题属于等积变形,圆柱的体积=长方体的体积;π×底面半径的平方×高=圆柱的体积,圆柱的体积÷长方体的高÷长方体的宽=长方体的长。
同课章节目录
