期中检测卷(含答案)---2024-2025学年五年级数学下册真题重组检测卷(浙教版)
文档属性
| 名称 | 期中检测卷(含答案)---2024-2025学年五年级数学下册真题重组检测卷(浙教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 349.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 21:07:05 | ||
图片预览




文档简介
保密★启用前
2024-2025学年五年级下册期中真题重组检测卷(浙教版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.(2021五下·惠来期中)一筐苹果,第一次卖出全部的 ,第二次卖出余下的 ,两次卖出比较,( ) 。
A.第一次多 B.第二次多 C.同样多 D.无法比较
2.(2024五下·薛城期中)下列分数中,不能化成有限小数的是( )
A. B. C.
3.(2024五下·章贡期中)正方体的棱长扩大到原来的2倍,则表面积就扩大到原来的 倍,体积就扩大到原来的 倍。
A.2 B.4 C.8 D.16
4.(2024五下·龙岗期中)五(3)班人数占全校总人数的,其中五(3)班男生占全班人数的,则五(3)班男生人数占全校总人数的( )
A. B. C. D.
5.(2024五下·龙海期中)下列说法正确的是( )
A.除了2以外,任意两个质数的和一定是偶数。
B.一个粉笔盒的体积约是1cm3。
C.两个连续自然数的和一定是奇数,积不一定是偶数。
D.在10g水中溶入7g盐,这时盐占盐水的。
6.(2024五下·隆回期中)下图中的阴影部分占整个图形的( )
A. B. C. D.
7.(2024五下·汉川期中)有一个长方体形状的物体,从三个不同方向看,看到①②③三个长方形,其中①长26厘米,宽19厘米;②长19厘米,宽0.7厘米;③长26厘米,宽0.7厘米.这个物体最有可能是( )。
A.衣柜 B.普通手机 C.数学书 D.橡皮擦
8.(2024五下·武昌期中)一个长6dm、宽4dm、高5dm的长方体盒子,最多能放( )个棱长为2dm的正方体木块。
A.15 B.14 C.13 D.12
9.(2024五下·蕲春期中)做同一种零件,王师傅2小时做15个,陈师傅3小时做20个,他们的工作效率相比,( )。
A.王师傅快 B.陈师傅快 C.一样快 D.无法确定
10.(2024五下·桑植期中)明明把一个正方体盒子沿着棱剪开,不能剪成以下的( )。
A. B. C. D.
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.(2023五下·蕉岭期中)表面积相等的两个长方体,它们的体积一定相等。
12.(2024五下·德州期中)把约分后是 ,和 大小相等,意义也相同。 ( )
13.(2024五下·腾冲期中)一瓶眼药水的容积约5立方分米。( )
14.(2024五下·道外期中)容积的计算方法与体积的计算方法是完全相同的,但要从里面量出长、宽、高。( )
15.(2024五下·嘉祥期中)三个连续的自然数,中间的一个数是三个数之和的。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.(2024五下·威县期中)如果一个正方体的表面积是96m2,它每个面的面积是 m2,这个正方体的棱长是 m。
17.(2024五下·瑞安期中)如图,一个长方体的底面是正方形,侧面展开也是正方形。这个长方体的表面积是 cm2,体积是 cm3。
18.(2024五下·瑞安期中)小海用棱长1cm的小正方体搭成了右图的几何体,一共用了 个小正方体;至少要添加 个同样的小正方体就能摆成一个长方体,它的体积是 立方厘米。
19.(2024五下·北仑期中)如图,有四种型号的塑料板各4块(单位:cm),若选择其中的6块拼一个长方体,则共有 种可能。
20.(2024五下·北仑期中)小米用24dm长的铁丝做了一个正方体框架,这个框架的棱长是 dm。如果在这个框架的表面糊一层纸,至少需要 dm2的纸,得到的正方体的体积是 dm3。
21.(2024五下·海门月考) 11时= 日 97毫升= 升 43分= 时
22.(2024五下·沂源期中) = ÷24=0.375= %= 折
23.(2024五下·威县期中)一个长方体的长是2 分米,宽是 分米,高是 分米,它的棱长总和是 分米;一个正方体的棱长是 分米,它的表面积是 平方分米。
24.(2024五下·罗山期中)120cm3= dm3 5.9m3= 3 dm3
L=60mL 84cm3= dm3= L
25.(2024五下·期中)端午节是我国的传统节日,人们有吃粽子的习俗,今年端午节,天天家包了许多粽子,妈妈先把 30 个肉粽平均分给几家邻居,接着又把 18 个蜜枣粽平均分给了这几家,都正好分完。这些粽子最多分给了 家邻居。
阅卷人 四、计算题(23分)
得分
26.(2024五下·威县期中)直接写得数。
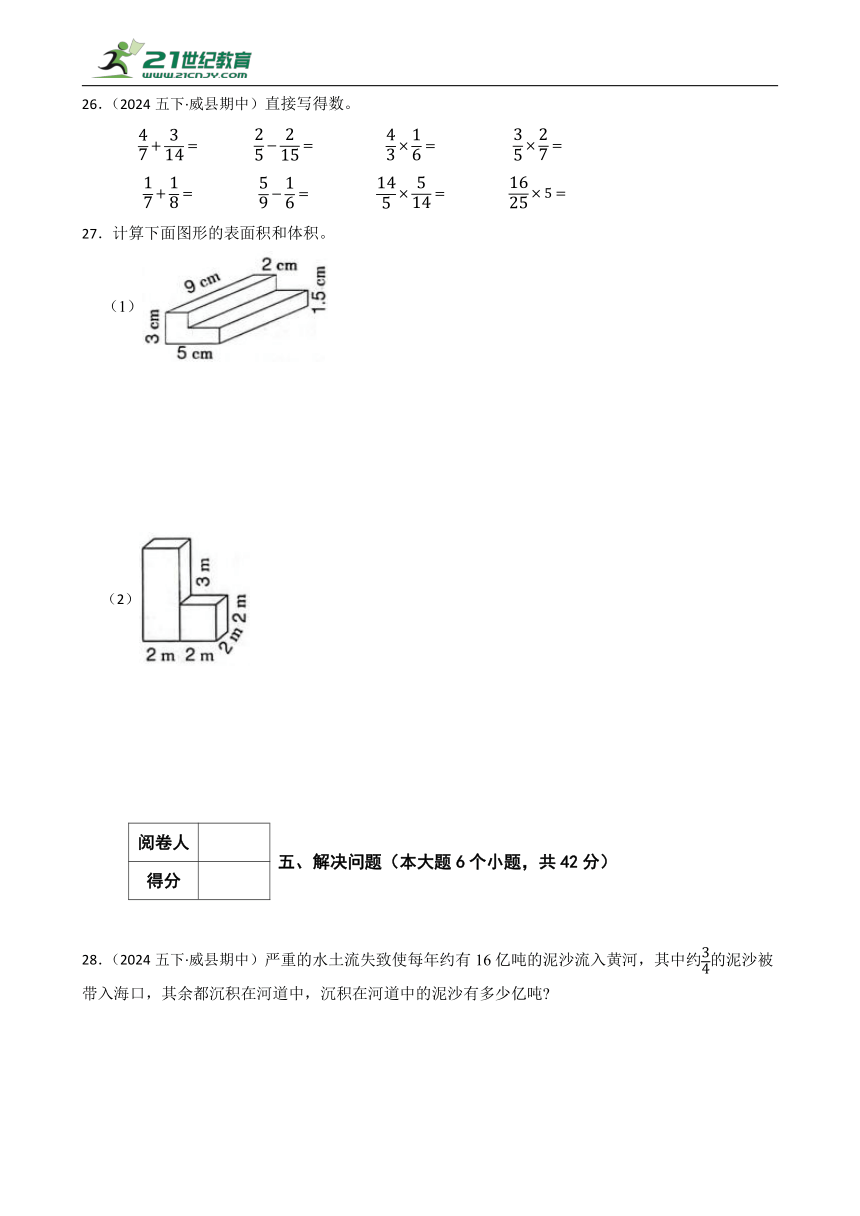
27.计算下面图形的表面积和体积。
(1)
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
28.(2024五下·威县期中)严重的水土流失致使每年约有16亿吨的泥沙流入黄河,其中约的泥沙被带入海口,其余都沉积在河道中,沉积在河道中的泥沙有多少亿吨
29.(2024五下·瑞安期中)李师傅根据下图所示的图纸做了一个长方体铁皮盒子(单位:cm),至少需要多少平方厘米的铁皮
30.(2024五下·北仑期中)在“庆六一”活动中,芦江书院学生用棱长为2cm的正方体塑料拼插积木,在操场上搭起了一面长6dm、宽2.4dm、高4dm的心愿墙。搭成这面墙一共用了多少块积木?
31.(2024五下·海门月考)把两根长度分别是45厘米和60厘米的铁丝截成长度相等的小段,每根都不能有剩余。每段最长是多少厘米?可以截成多少段?
32.(2024五下·惠阳期中)淘气有一根2m的彩带,第一次用去彩带全长的,第二次用去彩带全长的。这根彩带还剩全长的几分之几?
33.(2024五下·期中)小丽为妈妈选了一份生日礼物。(如图)礼品盒的体积是多少立方厘米?
答案解析部分
1.C
(1-)×
=×
=
两次卖出比较,同样多。
故答案为:C。
根据题意可知,把这筐苹果的总质量看成单位“1”,单位“1”-第一次卖出的占全部的分率=余下的占全部的分率,然后用余下的×=第二次卖出的占全部的分率,最后对比即可。
2.C
解:选项A:=,25=5×5,只包含质因数5,所以,这个分数能化成有限小数;
选项B:16=2×2×2×2,只包含质因数2,所以,这个分数能化成有限小数;
选项C:33=3×11,其中不包含质因数2和5,所以,这个分数不能化成有限小数;
故答案为:C。
当一个分数化简到最简形式后,其分母只包含质因数2和5,那么这个分数就可以化为有限小数,据此解答。
3.B;C
解:2×2=4
2×2×2=8。
故答案为:B;C。
正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。正方体的棱长扩大到原来的2倍,则表面积就扩大到原来的4倍,体积就扩大到原来的8倍。
4.D
解:×=。
故答案为:D。
五(3)班男生人数占全校总人数的分率=五(3)班人数占全校总人数的分率×五(3)班男生占全班人数的分率。
5.A
解:A:除了2以外,任何质数都是奇数,任意两个质数的和一定是偶数。原题说法正确;
B:一个粉笔盒的体积约是1dm3, 原题说法错误;
C:两个连续自然数的积一定是偶数。原题说法错误;
D:10+7=17(克),7÷17=,这时盐占盐水的,原题说法错误。
故答案为:A。
个位上是1、3、5、7、9的数是奇数;个位上是0、2、4、6、8的数是偶数;
一个数,如果只有1和它本身两个因数,这样的数叫做质数;
盐的质量+水的质量=盐水的质量,盐的质量÷盐水的质量=盐占盐水的分率。
6.C
解:把一个长方形看作单位“1”,把它平均分成8份,每份是,其中有5份涂阴影,也就是5个,即。
故答案为:C。
把单位“1”平均分成若干份,用分数表示时,分母是分成的份数,分子是要表示的份数。
7.C
解:这个物体长26厘米、宽19厘米、高0.7米,则可能是数学书。
故答案为:C。
依据对长方体的认识、依据具体数据判断可能是数学书。
8.D
解:6÷2=3(个)
4÷2=2(个)
5÷2=2(个)······1(分米)
3×2×2=12(个)
故答案为:D。
最多能放棱长为2dm的正方体木块的个数=长边能放的个数×宽边能放的个数×高边能放的个数。
9.A
解:15÷2=
20÷3=
故王师傅 的工作效率快。
故答案为:A。
根据分数与除法的关系,求出王师傅和陈师傅的工作效率,再进行比较即可。
10.C
解:明明把一个正方体盒子沿着棱剪开,不能剪成。
故答案为:C。
不是正方体的展开图。
11.错误
根据分析可得,例如:长宽高分别为4,8,12的长方体表面积为:
(4×8+4×12+8×12)×2
=(32+48+96)×2
=176×2
=352,
体积为:
4×8×12
=32×12
=384;
长宽高分别为4,4,20的长方体表面积为:
(4×4+4×20+4×20)×2
=(16+80+80)×2
=176×2
=352,
体积为:
4×4×20
=16×20
=320;
表面积相等的两个长方体,它们的体积不一定相等,原题说法错误.
故答案为:错误.
此题主要考查了长方体的表面积和体积的计算,可以用举例的方法,列举两个表面积相等的长方体,通过计算发现体积不相等,据此解答.
12.错误
解: 把约分后是 ,和 大小相等,意义不同,代表的是“1”被平均分成了6份,取其中的3份,而则是“1”被平均分成了2份,取其中的1份,原题说法错误。
故答案为:错误。
分数的约分是将一个分数的分子和分母同时除以它们的公因数,以得到一个与原分数值相等但形式上更简单的分数;约分后大小不变,意义变了。
13.错误
解:一瓶眼药水的容积约5立方厘米,也就是5毫升。原题说法错误。
故答案为:错误。
1立方分米=1升,1立方厘米=1毫升;容积的常用单位有升、毫升;根据实际情况并结合题中的数字选择合适的单位。
14.正确
解:长方体或正方体容器容积的计算方法,跟体积的计算方法相同,但要从容器里面量长、宽、高。原题说法正确。
故答案为:正确。
物体所占空间的大小叫做物体的体积;容器所能容纳物体的体积叫做它们的容积。体积和容积的公式都是V=Sh,它们的计算方法相同,但容积的尺寸是在容器里面量长、宽、高,体积则从物体的外面测量长、宽、高。
15.正确
解:假设中间的一个数是x,则
x÷[(x-1)+x+(x+1)]
=x÷3x
=
故原说法正确。
故答案为:正确。
相邻的自然数之间相差1,假设中间的一个数是x,则较小的一个数是(x-1),较大的一个数是(x+1),中间数+三个数的和=中间的一个数是三个数之和的几分之几。
16.16;4
解:96÷6=16(平方米)
16÷4=4(米)。
故答案为:16;4。
正方体每个面的面积=正方体的表面积÷6,这个正方体的棱长×棱长=每个面的面积。
17.450;500
解:20÷4=5(厘米)
(5×5+5×20+5×20)×2
=(25+100+100)×2
=225×2
=450(平方厘米)
5×5×20
=25×20
=500(立方厘米)。
故答案为:450;500。
这个长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高;其中,长=宽=高÷4。
18.6;10;16
解:5+1=6(个)
8×2-6=10(个)
4×2×2
=8×2
=16(立方厘米)。
故答案为:6;10;16。
共用小正方体的个数=下面一层的个数+上面一层的个数;
摆成一个长方体至少要添加同样小正方体的个数=长方体每层的个数×2-现有小正方体的个数;
摆成长方体的体积=长×宽×高。
19.3
解:第一种:①2块、②2块、③2块,拼成长15厘米、宽10厘米、高7厘米的长方体;
第二种:①4块、④2块,拼成长15厘米、宽10厘米、高10厘米的长方体;
第三种:③4块、④2块,拼成长7厘米、宽10厘米、高10厘米的长方体。
故答案为:3。
长方体有6个长方形的面,相对的面完全相同,特殊情况下,相对的两个面是正方形,其余四个面是完全相同的长方形,据此拼一拼。
20.2;24;8
解:24÷12=2(分米)
2×2×6
=4×6
=24(平方分米)
2×2×2=8(立方分米)。
故答案为:2;24;8。
这个框架的棱长=棱长和÷12,正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。
21.;;
解:11÷24=(时)
97÷1000=(升)
43÷60=(时)
故答案为:;;。
时÷24=日,毫升÷1000=升,分÷60=时。
22.3;9;37.5;三点七五
解:0.375=;==9÷24;所以=9÷24=0.375=37.5%=三点七五折。
故答案为:3;9;37.5;三点七五。
把小数写成分母是1000的分数并化成最简分数。分数的分子相当于被除数,分母相当于除数,根据分数与除法的关系确定被除数。把小数的小数点向右移动两位再加上百分号化成百分数。根据百分数确定折扣。
23.;
解:(++)×4
=×4
=(分米)
××6
=×6
=(平方分米)。
故答案为:;。
长方体的棱长和=(长+宽+高)×4,正方体的表面积=棱长×棱长×6。
24.0.12;5;900;0.06;0.084;0.084
解:120÷1000=0.12(立方分米),所以120立方厘米=0.12立方分米;
(5.9-5)×1000
=0.9×1000
=900(立方分米),所以5.9立方厘米=5立方米900立方分米;
60÷1000=0.06(升),所以0.06升=60毫升;
84÷1000=0.84(立方分米)=0.084升;所以84立方厘米=0.084立方分米=0.084升。
故答案为:0.12;5;900;0.06;0.084;0.084。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
25.6
解:30的因数有1、2、3、5、6、10、15、30;
18的因数有1、2、3、6、9、18;
30和18的公因数是1、2、3、6,
这些粽子最多分给了6家邻居。
故答案为:6。
30和18的最大公因数就是最多的邻居数,据此解答。
26.
1
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;
分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
27.(1)解:表面积:
(9×5+9×3+5×3)×2-(5-2)×(3-1.5)×2
=(45+27+15)×2-3×1.5×2
=87×2-9
=174-9
=165(cm2)
体积:
9×2×(3-1.5)+9×5×1.5
=18×1.5+45×1.5
=27+67.5
=94.5(cm3)
(2)解:表面积:
2×2×6+2×(2+3)×4
=24+40
=64(m2)
体积:
2×2×(3+2)+2×2×2
=20+8
=28(m3)
(1)图形的表面积比长9cm、宽5cm、高3cm的长方体的表面积少了两个长方形面的面积,这两个长方形的长都是(5-2)cm,宽都是(3-1.5)cm,由此计算表面积。图形的体积是下面长9cm、宽5cm、高1.5cm的长方体体积,加上上面长9cm、宽2cm、高是(3-1.5)cm的长方体体积。
(2)图形的表面积是左边长方体的表面积加上右边正方体4个面的面积,因此2×2的面一共有6个,2×(2+3)的面一共有4个。用左边长方体的体积加上右边正方体的体积就是它的体积。
28.解:16×(1-)
=16×
=4(亿吨)
答:沉积在河道中的泥沙有4亿吨。
沉积在河道中泥沙的质量=每年约流入黄河泥沙的质量×(1-被带入海口泥沙的分率)。
29.解:(48-20×2)÷2
=8÷2
=4(厘米)
(20×15+20×4+4×15)×2
=(300+80+60)×2
=440×2
=880(平方厘米)
答:至少需要880平方厘米的铁皮。
至少需要铁皮的面积=(长×宽+长×高+宽×高)×2,其中, 高=(48-长×2)÷2。
30.解:2厘米=0.2分米
(6×2.4×4)÷(0.2×0.2×0.2)
=57.6÷0.008
=7200(块)
答:搭成这面墙一共用了7200块积木。
搭成这面墙一共用积木的块数=(这面墙的长×宽×高)÷(积木的棱长×棱长×棱长)。
31.解:45=3×3×5,60=2×2×3×5,
45和60的最大公因数是3×5=15,
每段最长是15厘米,
(45+60)÷15=105÷15=7(段)
答:每段最长是15厘米,可以截成7段。
45和60的最大公因数就是每段最长的长度,两条线段的长度和÷45和60的最大公因数=可以截成的段数。
32.解:1--
=-
=
答:这根彩带还剩全长的。
这根彩带还剩下的分率=1-第一次用去的分率-第二次用去的分率。
33.解:30×25×15
=750×15
=11250(立方厘米)
答:礼品盒的体积是11250立方厘米。
根据长方体体积=长×宽×高。把数据代入公式解答。
2024-2025学年五年级下册期中真题重组检测卷(浙教版)
数学
考试时间:90分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷 客观题
阅卷人 一、单选题(本大题10个小题,每小题1分,共10分)
得分
1.(2021五下·惠来期中)一筐苹果,第一次卖出全部的 ,第二次卖出余下的 ,两次卖出比较,( ) 。
A.第一次多 B.第二次多 C.同样多 D.无法比较
2.(2024五下·薛城期中)下列分数中,不能化成有限小数的是( )
A. B. C.
3.(2024五下·章贡期中)正方体的棱长扩大到原来的2倍,则表面积就扩大到原来的 倍,体积就扩大到原来的 倍。
A.2 B.4 C.8 D.16
4.(2024五下·龙岗期中)五(3)班人数占全校总人数的,其中五(3)班男生占全班人数的,则五(3)班男生人数占全校总人数的( )
A. B. C. D.
5.(2024五下·龙海期中)下列说法正确的是( )
A.除了2以外,任意两个质数的和一定是偶数。
B.一个粉笔盒的体积约是1cm3。
C.两个连续自然数的和一定是奇数,积不一定是偶数。
D.在10g水中溶入7g盐,这时盐占盐水的。
6.(2024五下·隆回期中)下图中的阴影部分占整个图形的( )
A. B. C. D.
7.(2024五下·汉川期中)有一个长方体形状的物体,从三个不同方向看,看到①②③三个长方形,其中①长26厘米,宽19厘米;②长19厘米,宽0.7厘米;③长26厘米,宽0.7厘米.这个物体最有可能是( )。
A.衣柜 B.普通手机 C.数学书 D.橡皮擦
8.(2024五下·武昌期中)一个长6dm、宽4dm、高5dm的长方体盒子,最多能放( )个棱长为2dm的正方体木块。
A.15 B.14 C.13 D.12
9.(2024五下·蕲春期中)做同一种零件,王师傅2小时做15个,陈师傅3小时做20个,他们的工作效率相比,( )。
A.王师傅快 B.陈师傅快 C.一样快 D.无法确定
10.(2024五下·桑植期中)明明把一个正方体盒子沿着棱剪开,不能剪成以下的( )。
A. B. C. D.
阅卷人 二、判断题(本大题5个小题,每小题1分,共5分)
得分
11.(2023五下·蕉岭期中)表面积相等的两个长方体,它们的体积一定相等。
12.(2024五下·德州期中)把约分后是 ,和 大小相等,意义也相同。 ( )
13.(2024五下·腾冲期中)一瓶眼药水的容积约5立方分米。( )
14.(2024五下·道外期中)容积的计算方法与体积的计算方法是完全相同的,但要从里面量出长、宽、高。( )
15.(2024五下·嘉祥期中)三个连续的自然数,中间的一个数是三个数之和的。( )
阅卷人 三、填空题(本大题10个小题,每小题2分,共20分)
得分
16.(2024五下·威县期中)如果一个正方体的表面积是96m2,它每个面的面积是 m2,这个正方体的棱长是 m。
17.(2024五下·瑞安期中)如图,一个长方体的底面是正方形,侧面展开也是正方形。这个长方体的表面积是 cm2,体积是 cm3。
18.(2024五下·瑞安期中)小海用棱长1cm的小正方体搭成了右图的几何体,一共用了 个小正方体;至少要添加 个同样的小正方体就能摆成一个长方体,它的体积是 立方厘米。
19.(2024五下·北仑期中)如图,有四种型号的塑料板各4块(单位:cm),若选择其中的6块拼一个长方体,则共有 种可能。
20.(2024五下·北仑期中)小米用24dm长的铁丝做了一个正方体框架,这个框架的棱长是 dm。如果在这个框架的表面糊一层纸,至少需要 dm2的纸,得到的正方体的体积是 dm3。
21.(2024五下·海门月考) 11时= 日 97毫升= 升 43分= 时
22.(2024五下·沂源期中) = ÷24=0.375= %= 折
23.(2024五下·威县期中)一个长方体的长是2 分米,宽是 分米,高是 分米,它的棱长总和是 分米;一个正方体的棱长是 分米,它的表面积是 平方分米。
24.(2024五下·罗山期中)120cm3= dm3 5.9m3= 3 dm3
L=60mL 84cm3= dm3= L
25.(2024五下·期中)端午节是我国的传统节日,人们有吃粽子的习俗,今年端午节,天天家包了许多粽子,妈妈先把 30 个肉粽平均分给几家邻居,接着又把 18 个蜜枣粽平均分给了这几家,都正好分完。这些粽子最多分给了 家邻居。
阅卷人 四、计算题(23分)
得分
26.(2024五下·威县期中)直接写得数。
27.计算下面图形的表面积和体积。
(1)
阅卷人 五、解决问题(本大题6个小题,共42分)
得分
28.(2024五下·威县期中)严重的水土流失致使每年约有16亿吨的泥沙流入黄河,其中约的泥沙被带入海口,其余都沉积在河道中,沉积在河道中的泥沙有多少亿吨
29.(2024五下·瑞安期中)李师傅根据下图所示的图纸做了一个长方体铁皮盒子(单位:cm),至少需要多少平方厘米的铁皮
30.(2024五下·北仑期中)在“庆六一”活动中,芦江书院学生用棱长为2cm的正方体塑料拼插积木,在操场上搭起了一面长6dm、宽2.4dm、高4dm的心愿墙。搭成这面墙一共用了多少块积木?
31.(2024五下·海门月考)把两根长度分别是45厘米和60厘米的铁丝截成长度相等的小段,每根都不能有剩余。每段最长是多少厘米?可以截成多少段?
32.(2024五下·惠阳期中)淘气有一根2m的彩带,第一次用去彩带全长的,第二次用去彩带全长的。这根彩带还剩全长的几分之几?
33.(2024五下·期中)小丽为妈妈选了一份生日礼物。(如图)礼品盒的体积是多少立方厘米?
答案解析部分
1.C
(1-)×
=×
=
两次卖出比较,同样多。
故答案为:C。
根据题意可知,把这筐苹果的总质量看成单位“1”,单位“1”-第一次卖出的占全部的分率=余下的占全部的分率,然后用余下的×=第二次卖出的占全部的分率,最后对比即可。
2.C
解:选项A:=,25=5×5,只包含质因数5,所以,这个分数能化成有限小数;
选项B:16=2×2×2×2,只包含质因数2,所以,这个分数能化成有限小数;
选项C:33=3×11,其中不包含质因数2和5,所以,这个分数不能化成有限小数;
故答案为:C。
当一个分数化简到最简形式后,其分母只包含质因数2和5,那么这个分数就可以化为有限小数,据此解答。
3.B;C
解:2×2=4
2×2×2=8。
故答案为:B;C。
正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。正方体的棱长扩大到原来的2倍,则表面积就扩大到原来的4倍,体积就扩大到原来的8倍。
4.D
解:×=。
故答案为:D。
五(3)班男生人数占全校总人数的分率=五(3)班人数占全校总人数的分率×五(3)班男生占全班人数的分率。
5.A
解:A:除了2以外,任何质数都是奇数,任意两个质数的和一定是偶数。原题说法正确;
B:一个粉笔盒的体积约是1dm3, 原题说法错误;
C:两个连续自然数的积一定是偶数。原题说法错误;
D:10+7=17(克),7÷17=,这时盐占盐水的,原题说法错误。
故答案为:A。
个位上是1、3、5、7、9的数是奇数;个位上是0、2、4、6、8的数是偶数;
一个数,如果只有1和它本身两个因数,这样的数叫做质数;
盐的质量+水的质量=盐水的质量,盐的质量÷盐水的质量=盐占盐水的分率。
6.C
解:把一个长方形看作单位“1”,把它平均分成8份,每份是,其中有5份涂阴影,也就是5个,即。
故答案为:C。
把单位“1”平均分成若干份,用分数表示时,分母是分成的份数,分子是要表示的份数。
7.C
解:这个物体长26厘米、宽19厘米、高0.7米,则可能是数学书。
故答案为:C。
依据对长方体的认识、依据具体数据判断可能是数学书。
8.D
解:6÷2=3(个)
4÷2=2(个)
5÷2=2(个)······1(分米)
3×2×2=12(个)
故答案为:D。
最多能放棱长为2dm的正方体木块的个数=长边能放的个数×宽边能放的个数×高边能放的个数。
9.A
解:15÷2=
20÷3=
故王师傅 的工作效率快。
故答案为:A。
根据分数与除法的关系,求出王师傅和陈师傅的工作效率,再进行比较即可。
10.C
解:明明把一个正方体盒子沿着棱剪开,不能剪成。
故答案为:C。
不是正方体的展开图。
11.错误
根据分析可得,例如:长宽高分别为4,8,12的长方体表面积为:
(4×8+4×12+8×12)×2
=(32+48+96)×2
=176×2
=352,
体积为:
4×8×12
=32×12
=384;
长宽高分别为4,4,20的长方体表面积为:
(4×4+4×20+4×20)×2
=(16+80+80)×2
=176×2
=352,
体积为:
4×4×20
=16×20
=320;
表面积相等的两个长方体,它们的体积不一定相等,原题说法错误.
故答案为:错误.
此题主要考查了长方体的表面积和体积的计算,可以用举例的方法,列举两个表面积相等的长方体,通过计算发现体积不相等,据此解答.
12.错误
解: 把约分后是 ,和 大小相等,意义不同,代表的是“1”被平均分成了6份,取其中的3份,而则是“1”被平均分成了2份,取其中的1份,原题说法错误。
故答案为:错误。
分数的约分是将一个分数的分子和分母同时除以它们的公因数,以得到一个与原分数值相等但形式上更简单的分数;约分后大小不变,意义变了。
13.错误
解:一瓶眼药水的容积约5立方厘米,也就是5毫升。原题说法错误。
故答案为:错误。
1立方分米=1升,1立方厘米=1毫升;容积的常用单位有升、毫升;根据实际情况并结合题中的数字选择合适的单位。
14.正确
解:长方体或正方体容器容积的计算方法,跟体积的计算方法相同,但要从容器里面量长、宽、高。原题说法正确。
故答案为:正确。
物体所占空间的大小叫做物体的体积;容器所能容纳物体的体积叫做它们的容积。体积和容积的公式都是V=Sh,它们的计算方法相同,但容积的尺寸是在容器里面量长、宽、高,体积则从物体的外面测量长、宽、高。
15.正确
解:假设中间的一个数是x,则
x÷[(x-1)+x+(x+1)]
=x÷3x
=
故原说法正确。
故答案为:正确。
相邻的自然数之间相差1,假设中间的一个数是x,则较小的一个数是(x-1),较大的一个数是(x+1),中间数+三个数的和=中间的一个数是三个数之和的几分之几。
16.16;4
解:96÷6=16(平方米)
16÷4=4(米)。
故答案为:16;4。
正方体每个面的面积=正方体的表面积÷6,这个正方体的棱长×棱长=每个面的面积。
17.450;500
解:20÷4=5(厘米)
(5×5+5×20+5×20)×2
=(25+100+100)×2
=225×2
=450(平方厘米)
5×5×20
=25×20
=500(立方厘米)。
故答案为:450;500。
这个长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高;其中,长=宽=高÷4。
18.6;10;16
解:5+1=6(个)
8×2-6=10(个)
4×2×2
=8×2
=16(立方厘米)。
故答案为:6;10;16。
共用小正方体的个数=下面一层的个数+上面一层的个数;
摆成一个长方体至少要添加同样小正方体的个数=长方体每层的个数×2-现有小正方体的个数;
摆成长方体的体积=长×宽×高。
19.3
解:第一种:①2块、②2块、③2块,拼成长15厘米、宽10厘米、高7厘米的长方体;
第二种:①4块、④2块,拼成长15厘米、宽10厘米、高10厘米的长方体;
第三种:③4块、④2块,拼成长7厘米、宽10厘米、高10厘米的长方体。
故答案为:3。
长方体有6个长方形的面,相对的面完全相同,特殊情况下,相对的两个面是正方形,其余四个面是完全相同的长方形,据此拼一拼。
20.2;24;8
解:24÷12=2(分米)
2×2×6
=4×6
=24(平方分米)
2×2×2=8(立方分米)。
故答案为:2;24;8。
这个框架的棱长=棱长和÷12,正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。
21.;;
解:11÷24=(时)
97÷1000=(升)
43÷60=(时)
故答案为:;;。
时÷24=日,毫升÷1000=升,分÷60=时。
22.3;9;37.5;三点七五
解:0.375=;==9÷24;所以=9÷24=0.375=37.5%=三点七五折。
故答案为:3;9;37.5;三点七五。
把小数写成分母是1000的分数并化成最简分数。分数的分子相当于被除数,分母相当于除数,根据分数与除法的关系确定被除数。把小数的小数点向右移动两位再加上百分号化成百分数。根据百分数确定折扣。
23.;
解:(++)×4
=×4
=(分米)
××6
=×6
=(平方分米)。
故答案为:;。
长方体的棱长和=(长+宽+高)×4,正方体的表面积=棱长×棱长×6。
24.0.12;5;900;0.06;0.084;0.084
解:120÷1000=0.12(立方分米),所以120立方厘米=0.12立方分米;
(5.9-5)×1000
=0.9×1000
=900(立方分米),所以5.9立方厘米=5立方米900立方分米;
60÷1000=0.06(升),所以0.06升=60毫升;
84÷1000=0.84(立方分米)=0.084升;所以84立方厘米=0.084立方分米=0.084升。
故答案为:0.12;5;900;0.06;0.084;0.084。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
25.6
解:30的因数有1、2、3、5、6、10、15、30;
18的因数有1、2、3、6、9、18;
30和18的公因数是1、2、3、6,
这些粽子最多分给了6家邻居。
故答案为:6。
30和18的最大公因数就是最多的邻居数,据此解答。
26.
1
同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;
分数乘分数,能约分的先约分,然后分子相乘的积作分子,分母相乘的积作分母。
27.(1)解:表面积:
(9×5+9×3+5×3)×2-(5-2)×(3-1.5)×2
=(45+27+15)×2-3×1.5×2
=87×2-9
=174-9
=165(cm2)
体积:
9×2×(3-1.5)+9×5×1.5
=18×1.5+45×1.5
=27+67.5
=94.5(cm3)
(2)解:表面积:
2×2×6+2×(2+3)×4
=24+40
=64(m2)
体积:
2×2×(3+2)+2×2×2
=20+8
=28(m3)
(1)图形的表面积比长9cm、宽5cm、高3cm的长方体的表面积少了两个长方形面的面积,这两个长方形的长都是(5-2)cm,宽都是(3-1.5)cm,由此计算表面积。图形的体积是下面长9cm、宽5cm、高1.5cm的长方体体积,加上上面长9cm、宽2cm、高是(3-1.5)cm的长方体体积。
(2)图形的表面积是左边长方体的表面积加上右边正方体4个面的面积,因此2×2的面一共有6个,2×(2+3)的面一共有4个。用左边长方体的体积加上右边正方体的体积就是它的体积。
28.解:16×(1-)
=16×
=4(亿吨)
答:沉积在河道中的泥沙有4亿吨。
沉积在河道中泥沙的质量=每年约流入黄河泥沙的质量×(1-被带入海口泥沙的分率)。
29.解:(48-20×2)÷2
=8÷2
=4(厘米)
(20×15+20×4+4×15)×2
=(300+80+60)×2
=440×2
=880(平方厘米)
答:至少需要880平方厘米的铁皮。
至少需要铁皮的面积=(长×宽+长×高+宽×高)×2,其中, 高=(48-长×2)÷2。
30.解:2厘米=0.2分米
(6×2.4×4)÷(0.2×0.2×0.2)
=57.6÷0.008
=7200(块)
答:搭成这面墙一共用了7200块积木。
搭成这面墙一共用积木的块数=(这面墙的长×宽×高)÷(积木的棱长×棱长×棱长)。
31.解:45=3×3×5,60=2×2×3×5,
45和60的最大公因数是3×5=15,
每段最长是15厘米,
(45+60)÷15=105÷15=7(段)
答:每段最长是15厘米,可以截成7段。
45和60的最大公因数就是每段最长的长度,两条线段的长度和÷45和60的最大公因数=可以截成的段数。
32.解:1--
=-
=
答:这根彩带还剩全长的。
这根彩带还剩下的分率=1-第一次用去的分率-第二次用去的分率。
33.解:30×25×15
=750×15
=11250(立方厘米)
答:礼品盒的体积是11250立方厘米。
根据长方体体积=长×宽×高。把数据代入公式解答。
同课章节目录
