数学:4.4《对数的概念及运算》教案(1)(沪教版高一下)
文档属性
| 名称 | 数学:4.4《对数的概念及运算》教案(1)(沪教版高一下) |

|
|
| 格式 | rar | ||
| 文件大小 | 34.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-18 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
课题4.4 对数的概念及运算(1)——对数的概念
1、 教学内容分析
为了解决“已知底数和幂的值,求指数的问题”,我们引入了新
的知识——对数。本节课是对数问题的第一课时,考虑到学生在接受新知识时可能存在的疑惑,因此要在对数概念的形成上重点讲解,和学生共同经历由指数式提出对数概念的过程。由于指对数之间存在着互相转化的关系,所以我们可以结合指数的性质特点考察对数中对于底数、真数以及对数的取值范围的要求。
二、教学目标设计
1.理解对数的意义,掌握底数、真数、对数的允许值范围;
2.掌握对数式与指数式的互化,理解对数式中的底数、真数、对数与指数式中底数、幂、指数之间的对应关系;
3.知道特殊对数的表示方法,会利用计算器计算常用对数值;
4. 经历由指数式提出对数概念的过程;
5. 养成类比、转化的思维习惯;
三、教学重点及难点
对数式与指数式的互化
四、教学用具准备
多媒体课件
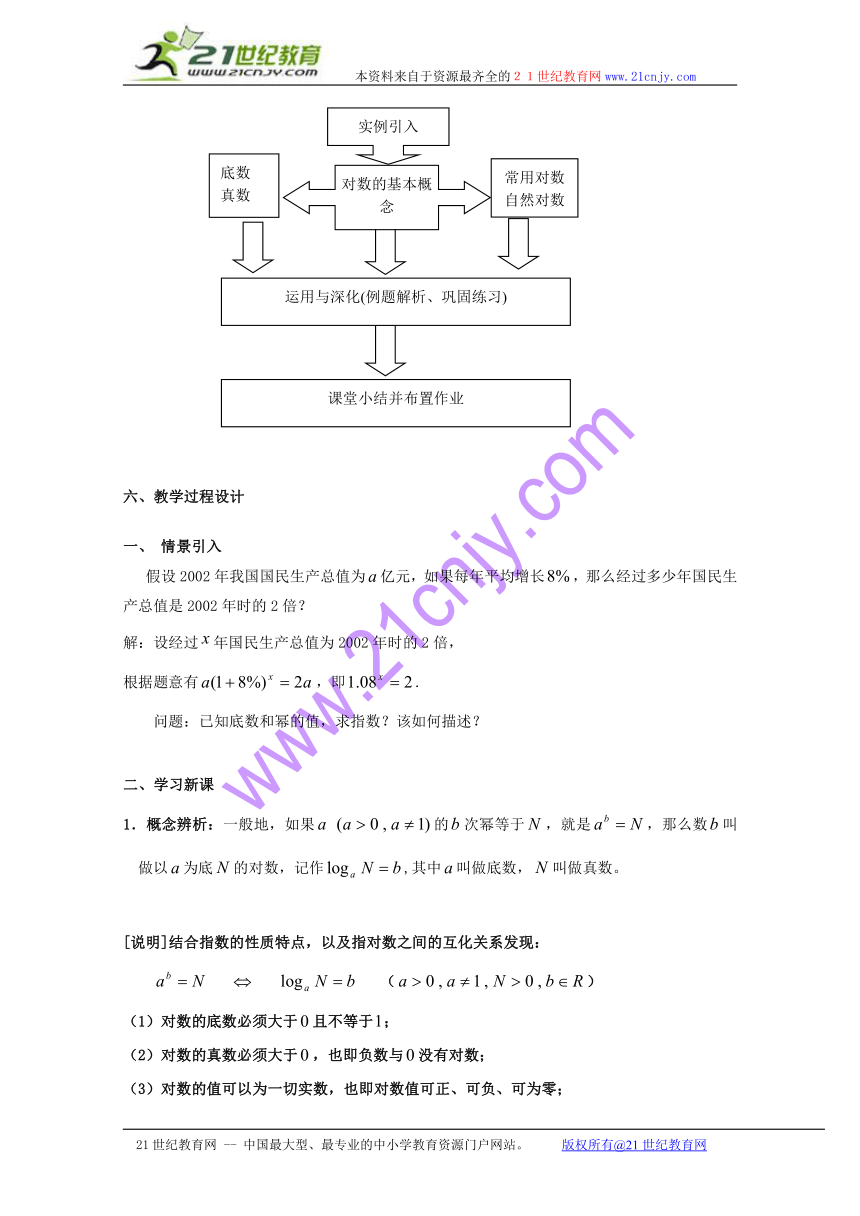
五、教学流程设计
六、教学过程设计
一、 情景引入
假设2002年我国国民生产总值为亿元,如果每年平均增长,那么经过多少年国民生产总值是2002年时的2倍?
解:设经过年国民生产总值为2002年时的2倍,
根据题意有,即.
问题:已知底数和幂的值,求指数?该如何描述?
二、学习新课
1.概念辨析:一般地,如果的次幂等于,就是,那么数叫做以为底的对数,记作,其中叫做底数,叫做真数。
[说明]结合指数的性质特点,以及指对数之间的互化关系发现:
()
(1)对数的底数必须大于且不等于;
(2)对数的真数必须大于,也即负数与没有对数;
(3)对数的值可以为一切实数,也即对数值可正、可负、可为零;
(4)通常以10为底的对数,叫做常用对数。为了简便,的常用对数,简记作;
(5)将以无理数为底的对数叫做自然对数。为了简便,的自然对数简记作
2.例题分析
例1、将下列指数式化为对数式
① ; ② ; ③; ④
例2、将下列对数式化为指数式:
① ; ② ; ③ ; ④ ;
例3、求下列各式的值:
① ; ② ; ③ ();
④ ; ⑤ ();
3.问题拓展
问题1、
(1)用计算器计算下列各数的值(结果精确到0.01)
348 0.02 82 2.83 0.3
(2)猜想真数为何值时,对数为正或者为负;
(3)用指数函数的性质解释你的结论.
[说明]
1.通过本例养成观察、思考的习惯;锻炼归纳问题的能力。
2.你能否模仿此例研究自然对数,从而得到你的结论?
问题2、证明:(),并利用结论求出下列各式的值:
① ; ② ; ③ ; ④ ;
⑤ ()
三、巩固练习
1.把下列指数式写成对数式:
(1); (2); (3); (4);
2.把下列对数式写成指数式:
(1); (2); (3)
(4); (5)();
3.利用计算器求值探索规律,并用指数函数性质解释你的结论:
(1); (2)23.8; (3); (4)10; (5)108
四、课堂小结
1.对数的基本概念、自然对数、常用对数;
2.指数式与对数式的互相转化。
五、作业布置
练习册4.4(A)组:1、2、3
七、教学设计说明
1.本节课是对数问题的第一课时。考虑到学生在学习对数概念时可能遇到的“理解难、认知难、记忆难”等问题,因此在教学过程中选择从解指数方程,也即“已知底数和幂的值求指数”这一角度入手,与学生共同经历从指数式转化成对数式的过程,期望通过实践加深学生对于对数产生的认识,使学生体会到学习对数的实际意义。
2.在处理指、对数式之间的转化时,从一个具体的指数方程
出发推广到一般的形式,结合指数函数的性质,由学生自己归纳出对数式中各字母的含义与其取值范围的要求。籍此过程中,将定义中的难点加以分散从而为下面让学生熟练应用指对数式之间的转化打下坚实的基础,并锻炼了学生的概括能力。整个过程,让学生经历了由特殊——一般——特殊的思维过程。
3.在学生掌握指对数式之间的转化后。利用计算器计算常用对数值并从中探索规律,结合指数函数的性质解释所得结论,调动学生参与讨论的积极性,锻炼学生的分析问题能力,树立学生类比的数学思想,并且为下一阶段对数函数的学习了打下基础。
对数的基本概念
常用对数
自然对数
实例引入
课堂小结并布置作业
底数
真数
运用与深化(例题解析、巩固练习)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
课题4.4 对数的概念及运算(1)——对数的概念
1、 教学内容分析
为了解决“已知底数和幂的值,求指数的问题”,我们引入了新
的知识——对数。本节课是对数问题的第一课时,考虑到学生在接受新知识时可能存在的疑惑,因此要在对数概念的形成上重点讲解,和学生共同经历由指数式提出对数概念的过程。由于指对数之间存在着互相转化的关系,所以我们可以结合指数的性质特点考察对数中对于底数、真数以及对数的取值范围的要求。
二、教学目标设计
1.理解对数的意义,掌握底数、真数、对数的允许值范围;
2.掌握对数式与指数式的互化,理解对数式中的底数、真数、对数与指数式中底数、幂、指数之间的对应关系;
3.知道特殊对数的表示方法,会利用计算器计算常用对数值;
4. 经历由指数式提出对数概念的过程;
5. 养成类比、转化的思维习惯;
三、教学重点及难点
对数式与指数式的互化
四、教学用具准备
多媒体课件
五、教学流程设计
六、教学过程设计
一、 情景引入
假设2002年我国国民生产总值为亿元,如果每年平均增长,那么经过多少年国民生产总值是2002年时的2倍?
解:设经过年国民生产总值为2002年时的2倍,
根据题意有,即.
问题:已知底数和幂的值,求指数?该如何描述?
二、学习新课
1.概念辨析:一般地,如果的次幂等于,就是,那么数叫做以为底的对数,记作,其中叫做底数,叫做真数。
[说明]结合指数的性质特点,以及指对数之间的互化关系发现:
()
(1)对数的底数必须大于且不等于;
(2)对数的真数必须大于,也即负数与没有对数;
(3)对数的值可以为一切实数,也即对数值可正、可负、可为零;
(4)通常以10为底的对数,叫做常用对数。为了简便,的常用对数,简记作;
(5)将以无理数为底的对数叫做自然对数。为了简便,的自然对数简记作
2.例题分析
例1、将下列指数式化为对数式
① ; ② ; ③; ④
例2、将下列对数式化为指数式:
① ; ② ; ③ ; ④ ;
例3、求下列各式的值:
① ; ② ; ③ ();
④ ; ⑤ ();
3.问题拓展
问题1、
(1)用计算器计算下列各数的值(结果精确到0.01)
348 0.02 82 2.83 0.3
(2)猜想真数为何值时,对数为正或者为负;
(3)用指数函数的性质解释你的结论.
[说明]
1.通过本例养成观察、思考的习惯;锻炼归纳问题的能力。
2.你能否模仿此例研究自然对数,从而得到你的结论?
问题2、证明:(),并利用结论求出下列各式的值:
① ; ② ; ③ ; ④ ;
⑤ ()
三、巩固练习
1.把下列指数式写成对数式:
(1); (2); (3); (4);
2.把下列对数式写成指数式:
(1); (2); (3)
(4); (5)();
3.利用计算器求值探索规律,并用指数函数性质解释你的结论:
(1); (2)23.8; (3); (4)10; (5)108
四、课堂小结
1.对数的基本概念、自然对数、常用对数;
2.指数式与对数式的互相转化。
五、作业布置
练习册4.4(A)组:1、2、3
七、教学设计说明
1.本节课是对数问题的第一课时。考虑到学生在学习对数概念时可能遇到的“理解难、认知难、记忆难”等问题,因此在教学过程中选择从解指数方程,也即“已知底数和幂的值求指数”这一角度入手,与学生共同经历从指数式转化成对数式的过程,期望通过实践加深学生对于对数产生的认识,使学生体会到学习对数的实际意义。
2.在处理指、对数式之间的转化时,从一个具体的指数方程
出发推广到一般的形式,结合指数函数的性质,由学生自己归纳出对数式中各字母的含义与其取值范围的要求。籍此过程中,将定义中的难点加以分散从而为下面让学生熟练应用指对数式之间的转化打下坚实的基础,并锻炼了学生的概括能力。整个过程,让学生经历了由特殊——一般——特殊的思维过程。
3.在学生掌握指对数式之间的转化后。利用计算器计算常用对数值并从中探索规律,结合指数函数的性质解释所得结论,调动学生参与讨论的积极性,锻炼学生的分析问题能力,树立学生类比的数学思想,并且为下一阶段对数函数的学习了打下基础。
对数的基本概念
常用对数
自然对数
实例引入
课堂小结并布置作业
底数
真数
运用与深化(例题解析、巩固练习)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
