华师大版八年级下册19.2菱形单元复习试题(附答案)
文档属性
| 名称 | 华师大版八年级下册19.2菱形单元复习试题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-19 16:31:28 | ||
图片预览


文档简介
华师大版八年级下册19.2菱形单元复习题
一、选择题
1、(2015滨州,第8题3分)顺次连接矩形ABCD各边中点,所得四边形必定是( D)
A. 邻边不等的平行四边形 B. 矩形 C. 正方形 D. 菱形
2、(2015娄底,第5题3分)下列命题中错误的是( C )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直
C. 同旁内角互补 D. 矩形的对角线相等
3、(2015,广西钦州,6,3分)如图,要使 ABCD成为菱形,则需添加的一个条件是( B )
A.AC=AD B.BA=BC C.∠ABC=90° D. AC=BD
4、(2014广西玉林市、防城港市,第6题3分)下列命题是假命题的是( C )
A.四个角相等的四边形是矩形 B. 对角线相等的平行四边形是矩形
C.对角线垂直的四边形是菱形 D. 对角线垂直的平行四边形是菱形
5、2014山东烟台,第6题3分)如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( C )
A. 28° B. 52° C. 62° D. 72°
6、(2015安徽, 第9题4分)如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( C )
A.2 B. 3 C. 5 D. 6
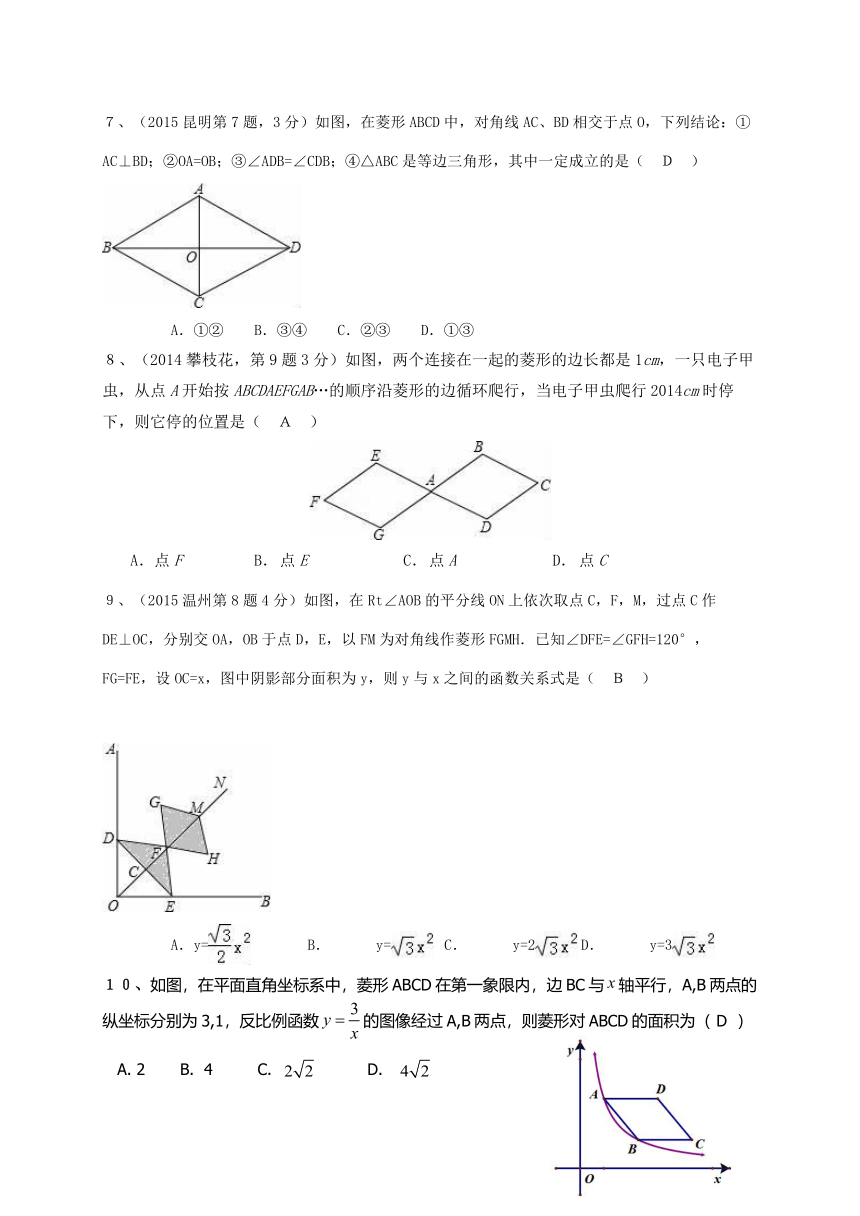
7、(2015昆明第7题,3分)如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形,其中一定成立的是( D )
A.①② B.③④ C.②③ D.①③
8、(2014攀枝花,第9题3分)如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( A )
A.点F B. 点E C. 点A D. 点C
9、(2015温州第8题4分)如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( B )
A.y= B. y= C. y=2 D. y=3
10、如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与轴平行,A,B两点的纵坐标分别为3,1,反比例函数的图像经过A,B两点,则菱形对ABCD的面积为( D )
A. 2 B. 4 C. D.
11、(2015四川攀枝花第10题3分)如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.其中正确的结论个数为( B )
A.4 B. 3 C. 2 D. 1
12、(2014年黑龙江牡丹江) (2014黑龙江牡丹江, 第8题3分)如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( D )
A. 3 B. 4 C. 1 D. 2
二、填空题
13、(2015乌鲁木齐,第14题4分)若菱形的周长为8,相邻两内角之比为3:1,则菱形的高是 .
14、(2015湘潭,第14题3分)已知菱形ABCD的面积为24cm2,若对角线AC=6cm,则这个菱形的边长为 5 cm.
15、(2014甘肃白银、临夏,第17题4分)如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 .
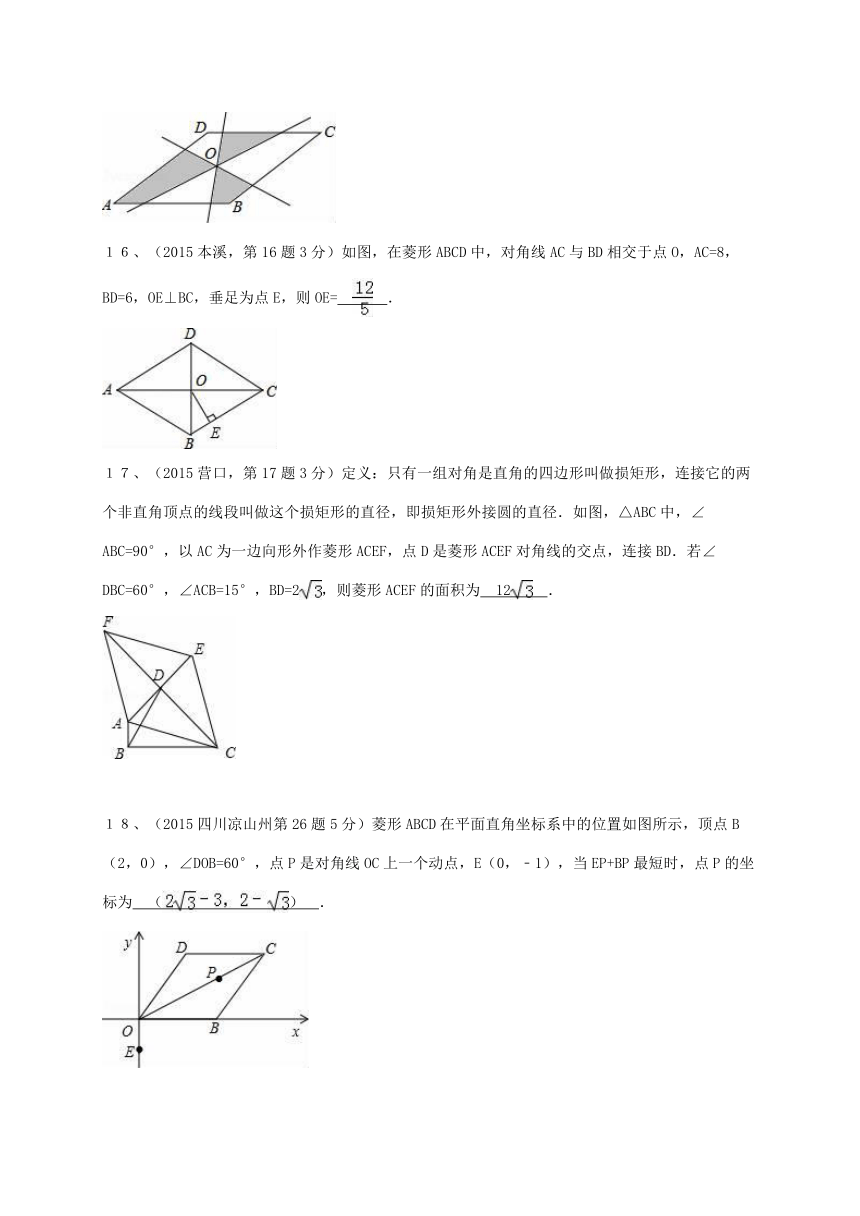
16、(2015本溪,第16题3分)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
17、(2015营口,第17题3分)定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径,即损矩形外接圆的直径.如图,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,连接BD.若∠DBC=60°,∠ACB=15°,BD=2,则菱形ACEF的面积为 12 .
18、(2015四川凉山州第26题5分)菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为 () .
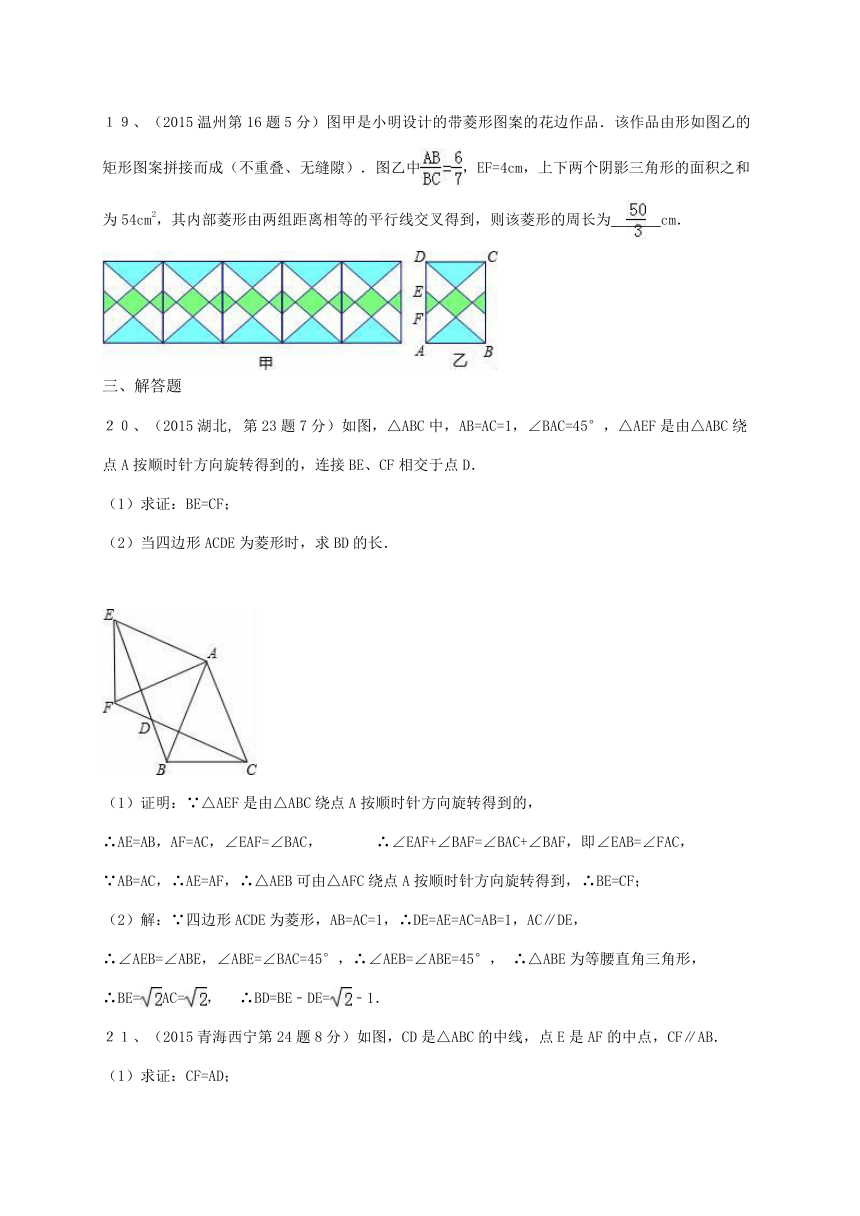
19、(2015温州第16题5分)图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成(不重叠、无缝隙).图乙中,EF=4cm,上下两个阴影三角形的面积之和为54cm2,其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为 cm.
三、解答题
20、(2015湖北, 第23题7分)如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC, ∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC, ∴AE=AF, ∴△AEB可由△AFC绕点A按顺时针方向旋转得到, ∴BE=CF;
(2)解:∵四边形ACDE为菱形,AB=AC=1,∴DE=AE=AC=AB=1,AC∥DE,
∴∠AEB=∠ABE,∠ABE=∠BAC=45°,∴∠AEB=∠ABE=45°, ∴△ABE为等腰直角三角形,
∴BE=AC=, ∴BD=BE﹣DE=﹣1.
21、(2015青海西宁第24题8分)如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
(1)求证:CF=AD;
(2)若∠ACB=90°,试判断四边形BFCD的形状,并说明理由.
解答: (1)证明∵AE是DC边上的中线,∴AE=FE,
∵CF∥AB,∴∠ADE=∠CFE,∠DAE=∠CFE.
在△ADE和△FCE中,
, ∴△ADE≌△FCE(AAS), ∴CF=DA.
(2)∵CD是△ABC的中线,
∴D是AB的中点, ∴AD=BD,
∵△ADE≌△FCE,∴AD=CF, ∴BD=CF, ∵AB∥CF,∴BD∥CF,
∴四边形BFCD是平行四边形, ∵∠ACB=90°,∴△ACB是直角三角形, ∴CD=AB,
∵BD=AB, ∴BD=CD, ∴四边形BFCD是菱形.
22、(2015黔南州)(第22题)如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
解答: 解:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD, ∵CF∥AB, ∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
, ∴△AED≌△CFD;
(2)∵△AED≌△CFD, ∴AE=CF,
∵EF为线段AC的垂直平分线,∴EC=EA,FC=FA, ∴EC=EA=FC=FA,
∴四边形AECF为菱形.
(3)∵AD=3,AE=5, ∴根据勾股定理得:ED=4, ∴EF=8,AC=6,
∴S菱形AECF=8×6÷2=24, ∴菱形AECF的面积是24
23、(2014四川遂宁,第20题,9分)已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
解: 证明:(1)∵CF∥BD,
∴∠DOE=∠CFE,
∵E是CD中点,
∴CE=DE,
在△ODE和△FCE中,
,
∴△ODE≌△FCE(ASA);
(2)∵△ODE≌△FCE,
∴OD=FC,
∵CF∥BD,
∴四边形ODFC是平行四边形,
在矩形ABCD中,OC=OD,
∴四边形ODFC是菱形.
24、(2014舟山,第20题8分)已知:如图,在 ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFED为菱形?请说明理由.
解 (1)证明:∵在 ABCD中,O为对角线BD的中点,
∴BO=DO,∠EDB=∠FBO,
在△EOD和△FOB中
,
∴△DOE≌△BOF(ASA);
(2)解:当∠DOE=90°时,四边形BFED为菱形,
理由:∵△DOE≌△BOF,
∴BF=DE,
又∵BF∥DE,
∴四边形EBFD是平行四边形,
∵BO=DO,∠EOD=90°,
∴EB=DE,
∴四边形BFED为菱形.
25、(2014莱芜,第21题9分)如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.
(1)求证:BE=CD;
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.
解答: 证明:(1)∵△ABC是等腰三角形,顶角∠BAC=α(α<60°),线段AD绕点A顺时针旋转α到AE,
∴AB=AC,
∴∠BAE=∠CAD,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴BE=CD;
(2)∵AD⊥BC,
∴BD=CD,
∴BE=BD=CD,∠BAD=∠CAD,
∴∠BAE=∠BAD,
在△ABD和△ABE中,
,
∴△ABD≌△ABE(SAS),
∴∠EBF=∠DBF,
∵EF∥BC,
∴∠DBF=∠EFB,
∴∠EBF=∠EFB,
∴EB=EF,
∴BD=BE=EF=FD,
∴四边形BDFE为菱形.
26、(2015江苏盐城,第26题10分)如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4,∠BAD=60°,且AB>4.
(1)求∠EPF的大小;
(2)若AP=6,求AE+AF的值;
(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.
解答: 解:(1)如图1,过点P作PG⊥EF于G,
∵PE=PF,
∴FG=EG=EF=,∠FPG=,
在△FPG中,sin∠FPG===,
∴∠FPG=60°,
∴∠EPF=2∠FPG=120°;
(2)如图2,过点P作PM⊥AB于M,PN⊥AD于N,
∵四边形ABCD是菱形,
∴AD=AB,DC=BC,
在△ABC与△ADC中,
,
∴△ABC≌△ADC,
∴∠DAC=∠BAC,
∴PM=PN,
在Rt△PME于Rt△PNF中,
,
∴Rt△PME≌Rt△PNF,
∴FN=EM,在Rt△PMA中,∠PMA=90°,∠PAM=∠DAB=30°,∴AM=APcos30°=3,同理AN=3,
∴AE+AF=(AM﹣EM)+(AN+NF)=6;
(3)如图3,当EF⊥AC,点P在EF的右侧时,AP有最大值,
当EF⊥AC,点P在EF的左侧时,AP有最小值,
设AC与EF交于点O,
∵PE=PF,
∴OF=EF=2,
∵∠FPA=60°,
∴OP=2,
∵∠BAD=60°,
∴∠FAO=30°,
∴AO=6,
∴AP=AO+PO=8,
同理AP′=AO﹣OP=4,
∴AP的最大值是8,最小值是4.
27、(2014黑龙江绥化,第26题9分)在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=PC.如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).
解答:
(1)提示:如图1:延长GP交DC于点E,
利用△PED≌△PGF,得出PE=PG,DE=FG,
∴CE=CG,
∴CP是EG的中垂线,
在RT△CPG中,∠PCG=60°,
∴PG=PC.
(2)如图2,延长GP交DA于点E,连接EC,GC,
∵∠ABC=60°,△BGF正三角形
∴GF∥BC∥AD,
∴∠EDP=∠GFP,[]
在△DPE和△FPG中
∴△DPE≌△FPG(ASA)
∴PE=PG,DE=FG=BG,
∵∠CDE=CBG=60°,CD=CB,
在△CDE和△CBG中,
∴△CDE≌△CBG(SAS)
∴CE=CG,∠DCE=∠BCG,
∴∠ECG=∠DCB=120°,
∵PE=PG,
∴CP⊥PG,∠PCG=∠ECG=60°
∴PG=PC.
(3)猜想:PG=PC.
证明:如图3,延长GP到H,使PH=PG,连接CH,CG,DH,作ME∥DC
∵P是线段DF的中点,
∴FP=DP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GF=HD,∠GFP=∠HDP,
∵∠GFP+∠PFE=120°,∠PFE=∠PDC,
∴∠CDH=∠HDP+∠PDC=120°,
∵四边形ABCD是菱形,
∴CD=CB,∠ADC=∠ABC=60°,点A、B、G又在一条直线上,
∴∠GBC=120°,
∵四边形BEFG是菱形,
∴GF=GB,
∴HD=GB,
∴△HDC≌△GBC,
∴CH=CG,∠DCH=∠BCG,
∴∠DCH+∠HCB=∠BCG+∠HCB=120°,
即∠HCG=120°
∵CH=CG,PH=PG,
∴PG⊥PC,∠GCP=∠HCP=60°,
∴PG=PC.
一、选择题
1、(2015滨州,第8题3分)顺次连接矩形ABCD各边中点,所得四边形必定是( D)
A. 邻边不等的平行四边形 B. 矩形 C. 正方形 D. 菱形
2、(2015娄底,第5题3分)下列命题中错误的是( C )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直
C. 同旁内角互补 D. 矩形的对角线相等
3、(2015,广西钦州,6,3分)如图,要使 ABCD成为菱形,则需添加的一个条件是( B )
A.AC=AD B.BA=BC C.∠ABC=90° D. AC=BD
4、(2014广西玉林市、防城港市,第6题3分)下列命题是假命题的是( C )
A.四个角相等的四边形是矩形 B. 对角线相等的平行四边形是矩形
C.对角线垂直的四边形是菱形 D. 对角线垂直的平行四边形是菱形
5、2014山东烟台,第6题3分)如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( C )
A. 28° B. 52° C. 62° D. 72°
6、(2015安徽, 第9题4分)如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( C )
A.2 B. 3 C. 5 D. 6
7、(2015昆明第7题,3分)如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形,其中一定成立的是( D )
A.①② B.③④ C.②③ D.①③
8、(2014攀枝花,第9题3分)如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( A )
A.点F B. 点E C. 点A D. 点C
9、(2015温州第8题4分)如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( B )
A.y= B. y= C. y=2 D. y=3
10、如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与轴平行,A,B两点的纵坐标分别为3,1,反比例函数的图像经过A,B两点,则菱形对ABCD的面积为( D )
A. 2 B. 4 C. D.
11、(2015四川攀枝花第10题3分)如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.其中正确的结论个数为( B )
A.4 B. 3 C. 2 D. 1
12、(2014年黑龙江牡丹江) (2014黑龙江牡丹江, 第8题3分)如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( D )
A. 3 B. 4 C. 1 D. 2
二、填空题
13、(2015乌鲁木齐,第14题4分)若菱形的周长为8,相邻两内角之比为3:1,则菱形的高是 .
14、(2015湘潭,第14题3分)已知菱形ABCD的面积为24cm2,若对角线AC=6cm,则这个菱形的边长为 5 cm.
15、(2014甘肃白银、临夏,第17题4分)如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 .
16、(2015本溪,第16题3分)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
17、(2015营口,第17题3分)定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径,即损矩形外接圆的直径.如图,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,点D是菱形ACEF对角线的交点,连接BD.若∠DBC=60°,∠ACB=15°,BD=2,则菱形ACEF的面积为 12 .
18、(2015四川凉山州第26题5分)菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为 () .
19、(2015温州第16题5分)图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成(不重叠、无缝隙).图乙中,EF=4cm,上下两个阴影三角形的面积之和为54cm2,其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为 cm.
三、解答题
20、(2015湖北, 第23题7分)如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC, ∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC, ∴AE=AF, ∴△AEB可由△AFC绕点A按顺时针方向旋转得到, ∴BE=CF;
(2)解:∵四边形ACDE为菱形,AB=AC=1,∴DE=AE=AC=AB=1,AC∥DE,
∴∠AEB=∠ABE,∠ABE=∠BAC=45°,∴∠AEB=∠ABE=45°, ∴△ABE为等腰直角三角形,
∴BE=AC=, ∴BD=BE﹣DE=﹣1.
21、(2015青海西宁第24题8分)如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
(1)求证:CF=AD;
(2)若∠ACB=90°,试判断四边形BFCD的形状,并说明理由.
解答: (1)证明∵AE是DC边上的中线,∴AE=FE,
∵CF∥AB,∴∠ADE=∠CFE,∠DAE=∠CFE.
在△ADE和△FCE中,
, ∴△ADE≌△FCE(AAS), ∴CF=DA.
(2)∵CD是△ABC的中线,
∴D是AB的中点, ∴AD=BD,
∵△ADE≌△FCE,∴AD=CF, ∴BD=CF, ∵AB∥CF,∴BD∥CF,
∴四边形BFCD是平行四边形, ∵∠ACB=90°,∴△ACB是直角三角形, ∴CD=AB,
∵BD=AB, ∴BD=CD, ∴四边形BFCD是菱形.
22、(2015黔南州)(第22题)如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
解答: 解:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD, ∵CF∥AB, ∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
, ∴△AED≌△CFD;
(2)∵△AED≌△CFD, ∴AE=CF,
∵EF为线段AC的垂直平分线,∴EC=EA,FC=FA, ∴EC=EA=FC=FA,
∴四边形AECF为菱形.
(3)∵AD=3,AE=5, ∴根据勾股定理得:ED=4, ∴EF=8,AC=6,
∴S菱形AECF=8×6÷2=24, ∴菱形AECF的面积是24
23、(2014四川遂宁,第20题,9分)已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
解: 证明:(1)∵CF∥BD,
∴∠DOE=∠CFE,
∵E是CD中点,
∴CE=DE,
在△ODE和△FCE中,
,
∴△ODE≌△FCE(ASA);
(2)∵△ODE≌△FCE,
∴OD=FC,
∵CF∥BD,
∴四边形ODFC是平行四边形,
在矩形ABCD中,OC=OD,
∴四边形ODFC是菱形.
24、(2014舟山,第20题8分)已知:如图,在 ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFED为菱形?请说明理由.
解 (1)证明:∵在 ABCD中,O为对角线BD的中点,
∴BO=DO,∠EDB=∠FBO,
在△EOD和△FOB中
,
∴△DOE≌△BOF(ASA);
(2)解:当∠DOE=90°时,四边形BFED为菱形,
理由:∵△DOE≌△BOF,
∴BF=DE,
又∵BF∥DE,
∴四边形EBFD是平行四边形,
∵BO=DO,∠EOD=90°,
∴EB=DE,
∴四边形BFED为菱形.
25、(2014莱芜,第21题9分)如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.
(1)求证:BE=CD;
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.
解答: 证明:(1)∵△ABC是等腰三角形,顶角∠BAC=α(α<60°),线段AD绕点A顺时针旋转α到AE,
∴AB=AC,
∴∠BAE=∠CAD,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴BE=CD;
(2)∵AD⊥BC,
∴BD=CD,
∴BE=BD=CD,∠BAD=∠CAD,
∴∠BAE=∠BAD,
在△ABD和△ABE中,
,
∴△ABD≌△ABE(SAS),
∴∠EBF=∠DBF,
∵EF∥BC,
∴∠DBF=∠EFB,
∴∠EBF=∠EFB,
∴EB=EF,
∴BD=BE=EF=FD,
∴四边形BDFE为菱形.
26、(2015江苏盐城,第26题10分)如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4,∠BAD=60°,且AB>4.
(1)求∠EPF的大小;
(2)若AP=6,求AE+AF的值;
(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.
解答: 解:(1)如图1,过点P作PG⊥EF于G,
∵PE=PF,
∴FG=EG=EF=,∠FPG=,
在△FPG中,sin∠FPG===,
∴∠FPG=60°,
∴∠EPF=2∠FPG=120°;
(2)如图2,过点P作PM⊥AB于M,PN⊥AD于N,
∵四边形ABCD是菱形,
∴AD=AB,DC=BC,
在△ABC与△ADC中,
,
∴△ABC≌△ADC,
∴∠DAC=∠BAC,
∴PM=PN,
在Rt△PME于Rt△PNF中,
,
∴Rt△PME≌Rt△PNF,
∴FN=EM,在Rt△PMA中,∠PMA=90°,∠PAM=∠DAB=30°,∴AM=APcos30°=3,同理AN=3,
∴AE+AF=(AM﹣EM)+(AN+NF)=6;
(3)如图3,当EF⊥AC,点P在EF的右侧时,AP有最大值,
当EF⊥AC,点P在EF的左侧时,AP有最小值,
设AC与EF交于点O,
∵PE=PF,
∴OF=EF=2,
∵∠FPA=60°,
∴OP=2,
∵∠BAD=60°,
∴∠FAO=30°,
∴AO=6,
∴AP=AO+PO=8,
同理AP′=AO﹣OP=4,
∴AP的最大值是8,最小值是4.
27、(2014黑龙江绥化,第26题9分)在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=PC.如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).
解答:
(1)提示:如图1:延长GP交DC于点E,
利用△PED≌△PGF,得出PE=PG,DE=FG,
∴CE=CG,
∴CP是EG的中垂线,
在RT△CPG中,∠PCG=60°,
∴PG=PC.
(2)如图2,延长GP交DA于点E,连接EC,GC,
∵∠ABC=60°,△BGF正三角形
∴GF∥BC∥AD,
∴∠EDP=∠GFP,[]
在△DPE和△FPG中
∴△DPE≌△FPG(ASA)
∴PE=PG,DE=FG=BG,
∵∠CDE=CBG=60°,CD=CB,
在△CDE和△CBG中,
∴△CDE≌△CBG(SAS)
∴CE=CG,∠DCE=∠BCG,
∴∠ECG=∠DCB=120°,
∵PE=PG,
∴CP⊥PG,∠PCG=∠ECG=60°
∴PG=PC.
(3)猜想:PG=PC.
证明:如图3,延长GP到H,使PH=PG,连接CH,CG,DH,作ME∥DC
∵P是线段DF的中点,
∴FP=DP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GF=HD,∠GFP=∠HDP,
∵∠GFP+∠PFE=120°,∠PFE=∠PDC,
∴∠CDH=∠HDP+∠PDC=120°,
∵四边形ABCD是菱形,
∴CD=CB,∠ADC=∠ABC=60°,点A、B、G又在一条直线上,
∴∠GBC=120°,
∵四边形BEFG是菱形,
∴GF=GB,
∴HD=GB,
∴△HDC≌△GBC,
∴CH=CG,∠DCH=∠BCG,
∴∠DCH+∠HCB=∠BCG+∠HCB=120°,
即∠HCG=120°
∵CH=CG,PH=PG,
∴PG⊥PC,∠GCP=∠HCP=60°,
∴PG=PC.
