第十六、十七章 二次根式和勾股定理 能力提升测试题(含答案)
文档属性
| 名称 | 第十六、十七章 二次根式和勾股定理 能力提升测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 16:55:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十六、十七章 二次根式和勾股定理 能力提升测试题
一.选择题(共10小题,满分30分)
1.下列式子中,属于最简二次根式的是( )
A. B. C. D.
2.满足下列关系的三条线段a,b,c组成的三角形一定是直角三角形的是( )
A.a<b+c B.a>b﹣c C.a=b=c D.a2=b2﹣c2
3.下列定理中没有逆定理的是( )
A.三边分别相等的两个三角形全等
B.直角三角形的两个锐角互余
C.斜边和一条直角边分别对应相等的两个直角三角形全等
D.全等三角形的对应角相等
4.下列计算中,正确的是( )
A. B.
C. D.
5.若△ABC的三边分别是a,b,c,则下列条件能判断△ABC是直角三角形的是( )
A.∠A=∠B=2∠C B.∠A:∠B:∠C=3:4:5
C.a=1,b=2,c=3 D.a=1,,
6.已知,则代数式x2+2x+1的值为( )
A.﹣2023 B.2023 C.﹣2024 D.2024
7.如图,Rt△ABC中,∠ACB=90°,,BC=6,点P为△ABC内一点,且满足PA2+PC2=AC2,当PB的长度最小时,△ACP的周长是( )
A. B. C. D.
8.如图,在数轴上以1个单位长度为边长画一个正方形,以表示数0的点为圆心,正方形的对角线长为半径画弧,与正半轴交于点A,则点A表示的数为( )
A. B. C. D.1
9.如图,从一个大正方形中裁去面积为12和27的两个小正方形,则剩下阴影部分的面积为( )
A.36 B.24 C. D.
10.如图,在△ABC中,∠ACB=90°,点D、E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处,若BC=12,AB=20,则CD的长为( )
A. B. C. D.6
二.填空题(共5小题,满分15分,每小题3分)
11.式子有意义,x的取值范围是 .
12.如图是一个简单的数值运算程序,当输入x的值为时,则输出的值为 .
13.已知a、b、c是一个三角形的三边长,如果满足(a﹣3)2|c﹣5|=0,则这个三角形的形状是 .
14.如图,长方形内有两个相邻的正方形(空白部分),其面积分别为3和12,则图中阴影部分的面积为 .
15.如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D,E在边BC上(点D在点E的左侧),连接BD,BE,使BD=BE,过点D,E分别作DF⊥AB于点F,EG⊥BC于点G,设线段DF=x,EG=y,则y与x的关系式为 .
三.解答题(共8小题,满分75分)
16.(8分)计算:
(1); (2).
17.(9分)计算:
(1); (2).
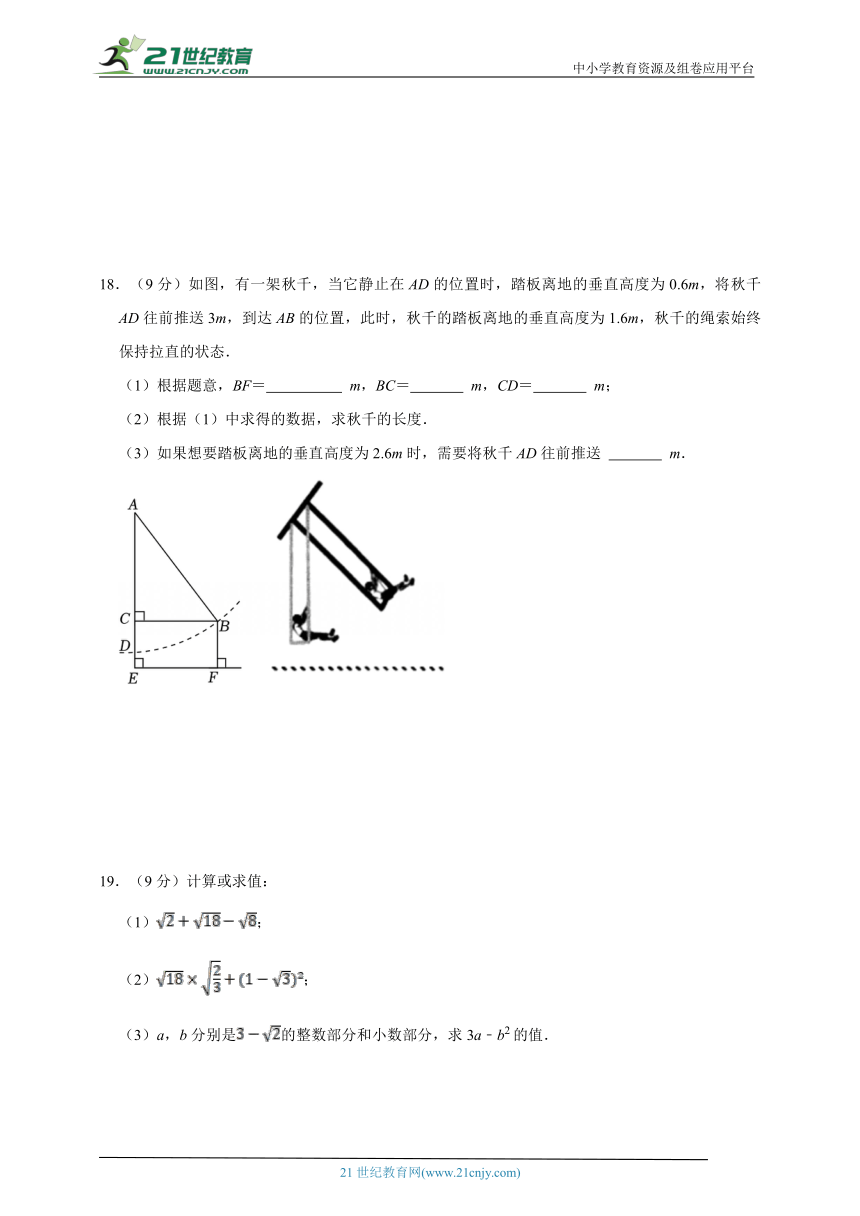
18.(9分)如图,有一架秋千,当它静止在AD的位置时,踏板离地的垂直高度为0.6m,将秋千AD往前推送3m,到达AB的位置,此时,秋千的踏板离地的垂直高度为1.6m,秋千的绳索始终保持拉直的状态.
(1)根据题意,BF= m,BC= m,CD= m;
(2)根据(1)中求得的数据,求秋千的长度.
(3)如果想要踏板离地的垂直高度为2.6m时,需要将秋千AD往前推送 m.
19.(9分)计算或求值:
(1);
(2);
(3)a,b分别是的整数部分和小数部分,求3a﹣b2的值.
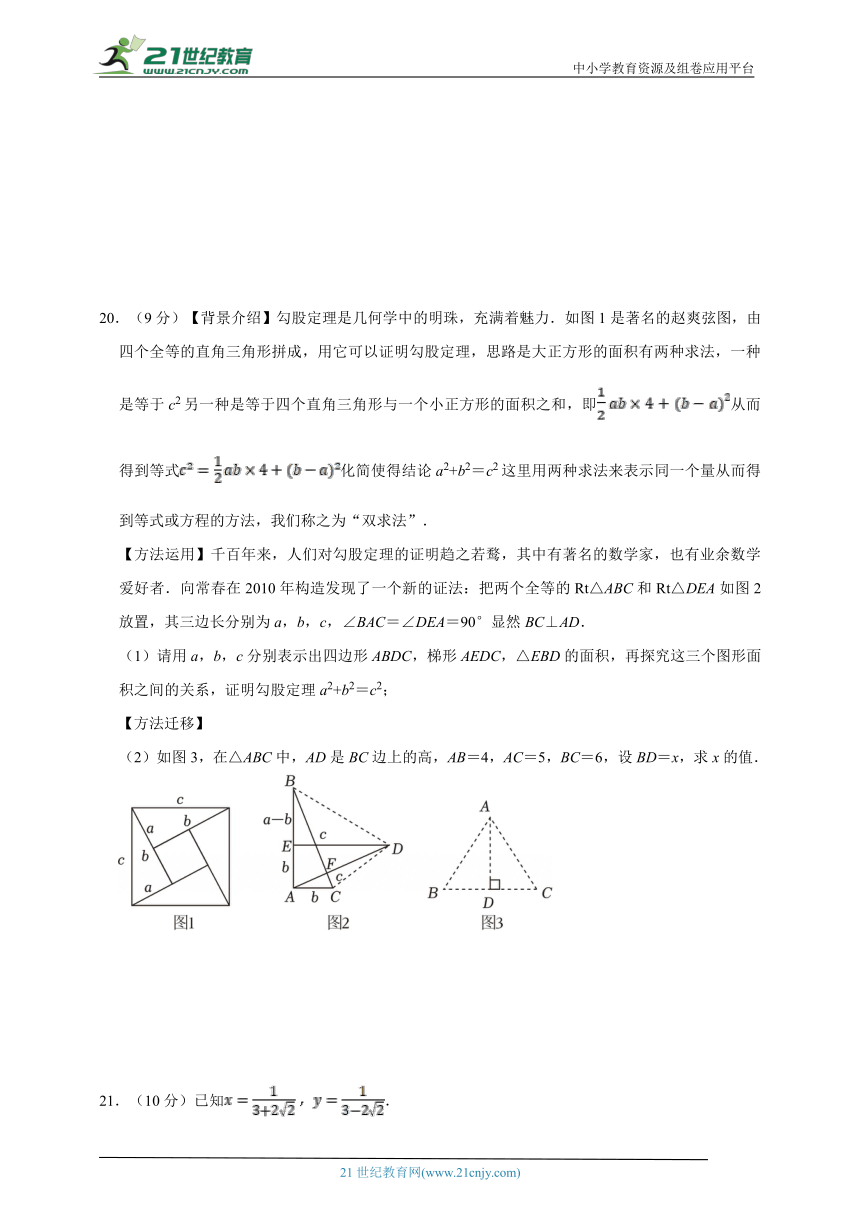
20.(9分)【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于c2另一种是等于四个直角三角形与一个小正方形的面积之和,即从而得到等式化简使得结论a2+b2=c2这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】千百年来,人们对勾股定理的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在2010年构造发现了一个新的证法:把两个全等的Rt△ABC和Rt△DEA如图2放置,其三边长分别为a,b,c,∠BAC=∠DEA=90°显然BC⊥AD.
(1)请用a,b,c分别表示出四边形ABDC,梯形AEDC,△EBD的面积,再探究这三个图形面积之间的关系,证明勾股定理a2+b2=c2;
【方法迁移】
(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
21.(10分)已知.
(1)求x2﹣3xy+y2的值;
(2)若x的小数部分为a,y的小数部分为b,求的值.
22.(10分)如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶端A在AC上,量得滑竿下端B距C点的距离为1.5米,当滑竿下端B向右移动0.5米到达D处时,求滑竿顶端A下滑多少米(即AE的长).
23.(11分)定义:若一个三角形存在两边平方和等于第三边平方的5倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由;
(2)若一个直角三角形是平方倍三角形,求该直角三角形的三边之比(结果按从小到大的顺序排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=4,CD为△ABC的中线,若△BCD是平方倍三角形,求△ABC的面积.
参考答案
一.选择题(共10小题,满分30分)
1.解:A.,不是最简二次根式,不符合题意;
B.,不是最简二次根式,不符合题意;
C.3,是最简二次根式,不符合题意;
D.是最简二次根式,符合题意.
选:D.
2.解:A.如a=3,b=4,c=6,符合a<b+c,但是此时三角形不是直角三角形,本选项不符合题意;
B.如a=3,b=6,c=4,符合a>b﹣c,但是此时三角形不是直角三角形,本选项不符合题意;
C.如a=b=c=2,三角形是等边三角形,但不是直角三角形,本选项不符合题意;
D.∵a2=b2﹣c2,
∴b2=a2+c2,
∴三角形是直角三角形,本选项符合题意;
选:D.
3.解:A、三边分别相等的两个三角形全等的逆命题是两个三角形全等的三边分别相等,是真命题,
则原命题有逆定理,不符合题意;
B、直角三角形的两个锐角互余的逆命题是两个锐角互余的三角形是直角三角形,是真命题,
则原命题有逆定理,不符合题意;
C、斜边和一条直角边分别对应相等的两个直角三角形全等的逆命题是两个全等的直角三角形斜边和一条直角边分别对应相等,是真命题,
则原命题有逆定理,不符合题意;
D、全等三角形的对应角相等的逆命题是对应角相等的三角形全等,是假命题,
则原命题没有逆定理,符合题意;
选:D.
4.解:与不是同类二次根式,不能合并,A错误,不符合题意;
32,B错误,不符合题意;
326,C错误,不符合题意;
3﹣1=2,D正确,符合题意;
选:D.
5.解:A、∵∠A=∠B=2∠C,且∠A+∠B+∠C=180°,
∴∠A=∠B=72°,∠C=36°,
∴△ABC不是直角三角形;
B、∵∠A:∠B:∠C=3:4:5,
∴∠C180°=75°,
∴△ABC不是直角三角形;
C、∵a=1,b=2,c=3,
∴a2+b2≠c2,
∴△ABC不是直角三角形;
D、∵a=1,b,c,
∴a2+b2=c2.
∴△ABC是直角三角形.
选:D.
6.解:∵,
∴x2+2x+1=(x+1)2
=(1+1)2
=2024,
选:D.
7.解:如图,取AC的中点O,连接OP,BO,
∵PA2+PC2=AC2.
∴∠APC=90°,
∴点P在以AC为直径的圆上运动,
在△BPO中,BP≥BO﹣OP,
∴当点P在线段BO上时,BP有最小值,
∵点O是AC的中点,∠APC=90°,
∴PO=AO=CO,
∴∠BOC=60°,
∴△COP是等边三角形,
∴∠PAC=30°,
∵,
∴PC=2,AP=26,
∴△ACP的周长是246=66.
选:A.
8.解:∵正方形的边长为1,
∴正方形对角线的长度,
∴OA,
点A表示.
选:C.
9.解:∵两个小正方形面积分别为12和27,
∴两个小正方形的边长分别为和,
∴大正方形的边长为:,
∴,A正确.
选:A.
10.解:∵∠ACB=90°,BC=12,AB=20,
∴AC16,
由对称性可知CF⊥DE,
又∵∠DCE=90°,
∴∠CDE=∠ECF=∠B,
∴CF=BF,
同理可得CF=AF,
∴F是AB的中点,
∴CFAB=10,
又∵∠DFC=∠ACF=∠A,∠DCF=∠FCA,
∴△CDF∽△CFA,
∴,
∴CF2=CD×CA,即102=CD×16,
∴CD,
选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:由题可知,
,
解得x≥2.
答案为:x≥2.
12.解:23,
则输出的值为3,
答案为:3.
13.解:∵(a﹣3)2|c﹣5|=0,(a﹣3)2≥0,0,|c﹣5|≥0,
∴a﹣3=0,b﹣4=0,c﹣5=0,
解得:a=3,b=4,c=5,
∵32+42=9+16=25=52,
∴这个三角形的形状是直角三角形.
答案为:直角三角形.
14.解:根据小空白正方形面积为3,得到边长为,大空白正方形面积为12,得到边长为,则阴影部分的长为,阴影部分的宽的和为,
则阴影部分面积为.
答案为:3.
15.解:如图,过点B作BH⊥AC于点H,
在Rt△ABC中,∠ABC=90°,AB=4,BC=3,
∴AC5,
∵BH⊥AC,
∴S△ABCAC BHAB BC,
∴BH,
在Rt△ABH中,由勾股定理得:AH,
∴CH=AC﹣AH=5,
∵DF⊥AB,EG⊥BC,
∴S△ABDAB DFAD BH,S△BCEBC EGCE BH,
∴AD,CE,
∵BD=BE,BH⊥DE,
∴DH=EH,
∴AH﹣AD=CH﹣CE,
即,
整理得:yx,
即y与x的关系式为yx,
答案为:yx.
三.解答题(共8小题,满分75分)
16.解:(1)23
=433
=4;
(2)
.
17.解:(1)
=2
=2;
(2)
=4.
18.解:(1)由题意得:BF=1.6m,BC=3m,DE=0.6m,
∵BF⊥EF,AE⊥EF,BC⊥AE,
∴四边形BCEF是矩形,
∴CE=BF=1.6m,
∴CD=CE﹣DE=1.6﹣0.6=1(m),
答案为:1.6,3,1;
(2)∵BC⊥AC,
∴∠ACB=90°,
设秋千的长度为x m,
则AB=AD=x m,AC=AD﹣CD=(x﹣1)m,
在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,
即(x﹣1)2+32=x2,
解得:x=5(m),
即秋千的长度是5m;
(3)当BF=2.6m时,CE=2.6m,
∵DE=0.6m,
∴CD=CE﹣DE=2.6﹣0.6=2(m),
由(2)可知,AD=AB=5m,
∴AC=AD﹣CD=5﹣2=3(m),
在Rt△ABC中,由勾股定理得:BC4(m),
即需要将秋千AD往前推送4m,
答案为:4.
19.解:(1)
;
(2)
=4;
(3)∵,
∴,
∵a,b分别是的整数部分和小数部分,
∴a=1,,
∴3a﹣b2.
20.(1)证明:∵S四边形ABCDc2,S梯形AEDC(b+a)b,,S四边形ABCD=S梯形AEDC+S△BED,
∴,
∴,
∴a2+b2=c2;
(2)解:在Rt△ABD中,由勾股定理得AD2=AB2﹣BD2=42﹣x2=16﹣x2,
∵BD+CD=BC=6,
∴CD=BC﹣BD=6﹣x,
在Rt△ACD中,由勾股定理得AD2=AC2﹣CD2=52﹣(6﹣x)2=﹣11+12x﹣x2,
∴16﹣x2=﹣11+12x﹣x2,
∴.
21.解:∵,
∴x=3﹣2,y=3+2,
(1)当x=3﹣2,y=3+2时,
x2﹣3xy+y2=(3﹣2)2﹣3(3﹣2)(3+2)+(3+2)2=9﹣128﹣27+24+9+128=31;
(2)∵x的小数部分为a,y的小数部分为b,
∴a=3﹣2,b=3+25=22,
∴(3﹣222)21+45=44.
22.解:设AE的长为x米,依题意得CE=(AC﹣x)米.
∵AB=DE=2.5,BC=1.5,∠C=90°,
∴AC2,
∵BD=0.5,
在Rt△ECD中,
CE
=1.5.
∴2﹣x=1.5,
∴x=0.5.
即AE=0.5.
答:滑杆顶端A下滑0.5米.
23.解:(1)结论:这个三角形不是“平方倍三角形”.
理由:∵22+()2=25,5×()2=25,
∴22+()2=5×()2,
∴这个三角形是“平方倍三角形”.
(2)设直角边长为a,b,斜边为c,
∵△ABC为“平方倍三角形”.
∴a2+b2=c2,且c2+a2=5b2,
∴2a2+b2=5b2,
∴ba,
∴ca,
∴b:a:c=1::;
(3)在Rt△ABC中,∠ACB=90°,CD为△ABC的中线,
∴AD=CD=DBAB,
∴∠B=∠DCB,∠A=∠DCA,
∵∠A+∠B+∠DCB+∠DCA=180°,
∴∠A+∠B=90°,
∴∠ACB=90°,
∴AB2=AC2+BC2=AC2+16,
∴AC2=AB2﹣16,
∵△BCD是平方倍三角形,
∴当CD2+BD2=5BC2=80,
∴AB2AB2=80,
∴AB2=160,
∴AC12,
∴△ABC的面积AC×BC=24;
当CD2+BC2=5BD2,
∴AB2+16=5AB2,
∴AB2=16=BC2(不合题意舍去),
综上所述:△ABC的面积为24.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第十六、十七章 二次根式和勾股定理 能力提升测试题
一.选择题(共10小题,满分30分)
1.下列式子中,属于最简二次根式的是( )
A. B. C. D.
2.满足下列关系的三条线段a,b,c组成的三角形一定是直角三角形的是( )
A.a<b+c B.a>b﹣c C.a=b=c D.a2=b2﹣c2
3.下列定理中没有逆定理的是( )
A.三边分别相等的两个三角形全等
B.直角三角形的两个锐角互余
C.斜边和一条直角边分别对应相等的两个直角三角形全等
D.全等三角形的对应角相等
4.下列计算中,正确的是( )
A. B.
C. D.
5.若△ABC的三边分别是a,b,c,则下列条件能判断△ABC是直角三角形的是( )
A.∠A=∠B=2∠C B.∠A:∠B:∠C=3:4:5
C.a=1,b=2,c=3 D.a=1,,
6.已知,则代数式x2+2x+1的值为( )
A.﹣2023 B.2023 C.﹣2024 D.2024
7.如图,Rt△ABC中,∠ACB=90°,,BC=6,点P为△ABC内一点,且满足PA2+PC2=AC2,当PB的长度最小时,△ACP的周长是( )
A. B. C. D.
8.如图,在数轴上以1个单位长度为边长画一个正方形,以表示数0的点为圆心,正方形的对角线长为半径画弧,与正半轴交于点A,则点A表示的数为( )
A. B. C. D.1
9.如图,从一个大正方形中裁去面积为12和27的两个小正方形,则剩下阴影部分的面积为( )
A.36 B.24 C. D.
10.如图,在△ABC中,∠ACB=90°,点D、E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处,若BC=12,AB=20,则CD的长为( )
A. B. C. D.6
二.填空题(共5小题,满分15分,每小题3分)
11.式子有意义,x的取值范围是 .
12.如图是一个简单的数值运算程序,当输入x的值为时,则输出的值为 .
13.已知a、b、c是一个三角形的三边长,如果满足(a﹣3)2|c﹣5|=0,则这个三角形的形状是 .
14.如图,长方形内有两个相邻的正方形(空白部分),其面积分别为3和12,则图中阴影部分的面积为 .
15.如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D,E在边BC上(点D在点E的左侧),连接BD,BE,使BD=BE,过点D,E分别作DF⊥AB于点F,EG⊥BC于点G,设线段DF=x,EG=y,则y与x的关系式为 .
三.解答题(共8小题,满分75分)
16.(8分)计算:
(1); (2).
17.(9分)计算:
(1); (2).
18.(9分)如图,有一架秋千,当它静止在AD的位置时,踏板离地的垂直高度为0.6m,将秋千AD往前推送3m,到达AB的位置,此时,秋千的踏板离地的垂直高度为1.6m,秋千的绳索始终保持拉直的状态.
(1)根据题意,BF= m,BC= m,CD= m;
(2)根据(1)中求得的数据,求秋千的长度.
(3)如果想要踏板离地的垂直高度为2.6m时,需要将秋千AD往前推送 m.
19.(9分)计算或求值:
(1);
(2);
(3)a,b分别是的整数部分和小数部分,求3a﹣b2的值.
20.(9分)【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于c2另一种是等于四个直角三角形与一个小正方形的面积之和,即从而得到等式化简使得结论a2+b2=c2这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】千百年来,人们对勾股定理的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在2010年构造发现了一个新的证法:把两个全等的Rt△ABC和Rt△DEA如图2放置,其三边长分别为a,b,c,∠BAC=∠DEA=90°显然BC⊥AD.
(1)请用a,b,c分别表示出四边形ABDC,梯形AEDC,△EBD的面积,再探究这三个图形面积之间的关系,证明勾股定理a2+b2=c2;
【方法迁移】
(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
21.(10分)已知.
(1)求x2﹣3xy+y2的值;
(2)若x的小数部分为a,y的小数部分为b,求的值.
22.(10分)如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶端A在AC上,量得滑竿下端B距C点的距离为1.5米,当滑竿下端B向右移动0.5米到达D处时,求滑竿顶端A下滑多少米(即AE的长).
23.(11分)定义:若一个三角形存在两边平方和等于第三边平方的5倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由;
(2)若一个直角三角形是平方倍三角形,求该直角三角形的三边之比(结果按从小到大的顺序排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=4,CD为△ABC的中线,若△BCD是平方倍三角形,求△ABC的面积.
参考答案
一.选择题(共10小题,满分30分)
1.解:A.,不是最简二次根式,不符合题意;
B.,不是最简二次根式,不符合题意;
C.3,是最简二次根式,不符合题意;
D.是最简二次根式,符合题意.
选:D.
2.解:A.如a=3,b=4,c=6,符合a<b+c,但是此时三角形不是直角三角形,本选项不符合题意;
B.如a=3,b=6,c=4,符合a>b﹣c,但是此时三角形不是直角三角形,本选项不符合题意;
C.如a=b=c=2,三角形是等边三角形,但不是直角三角形,本选项不符合题意;
D.∵a2=b2﹣c2,
∴b2=a2+c2,
∴三角形是直角三角形,本选项符合题意;
选:D.
3.解:A、三边分别相等的两个三角形全等的逆命题是两个三角形全等的三边分别相等,是真命题,
则原命题有逆定理,不符合题意;
B、直角三角形的两个锐角互余的逆命题是两个锐角互余的三角形是直角三角形,是真命题,
则原命题有逆定理,不符合题意;
C、斜边和一条直角边分别对应相等的两个直角三角形全等的逆命题是两个全等的直角三角形斜边和一条直角边分别对应相等,是真命题,
则原命题有逆定理,不符合题意;
D、全等三角形的对应角相等的逆命题是对应角相等的三角形全等,是假命题,
则原命题没有逆定理,符合题意;
选:D.
4.解:与不是同类二次根式,不能合并,A错误,不符合题意;
32,B错误,不符合题意;
326,C错误,不符合题意;
3﹣1=2,D正确,符合题意;
选:D.
5.解:A、∵∠A=∠B=2∠C,且∠A+∠B+∠C=180°,
∴∠A=∠B=72°,∠C=36°,
∴△ABC不是直角三角形;
B、∵∠A:∠B:∠C=3:4:5,
∴∠C180°=75°,
∴△ABC不是直角三角形;
C、∵a=1,b=2,c=3,
∴a2+b2≠c2,
∴△ABC不是直角三角形;
D、∵a=1,b,c,
∴a2+b2=c2.
∴△ABC是直角三角形.
选:D.
6.解:∵,
∴x2+2x+1=(x+1)2
=(1+1)2
=2024,
选:D.
7.解:如图,取AC的中点O,连接OP,BO,
∵PA2+PC2=AC2.
∴∠APC=90°,
∴点P在以AC为直径的圆上运动,
在△BPO中,BP≥BO﹣OP,
∴当点P在线段BO上时,BP有最小值,
∵点O是AC的中点,∠APC=90°,
∴PO=AO=CO,
∴∠BOC=60°,
∴△COP是等边三角形,
∴∠PAC=30°,
∵,
∴PC=2,AP=26,
∴△ACP的周长是246=66.
选:A.
8.解:∵正方形的边长为1,
∴正方形对角线的长度,
∴OA,
点A表示.
选:C.
9.解:∵两个小正方形面积分别为12和27,
∴两个小正方形的边长分别为和,
∴大正方形的边长为:,
∴,A正确.
选:A.
10.解:∵∠ACB=90°,BC=12,AB=20,
∴AC16,
由对称性可知CF⊥DE,
又∵∠DCE=90°,
∴∠CDE=∠ECF=∠B,
∴CF=BF,
同理可得CF=AF,
∴F是AB的中点,
∴CFAB=10,
又∵∠DFC=∠ACF=∠A,∠DCF=∠FCA,
∴△CDF∽△CFA,
∴,
∴CF2=CD×CA,即102=CD×16,
∴CD,
选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:由题可知,
,
解得x≥2.
答案为:x≥2.
12.解:23,
则输出的值为3,
答案为:3.
13.解:∵(a﹣3)2|c﹣5|=0,(a﹣3)2≥0,0,|c﹣5|≥0,
∴a﹣3=0,b﹣4=0,c﹣5=0,
解得:a=3,b=4,c=5,
∵32+42=9+16=25=52,
∴这个三角形的形状是直角三角形.
答案为:直角三角形.
14.解:根据小空白正方形面积为3,得到边长为,大空白正方形面积为12,得到边长为,则阴影部分的长为,阴影部分的宽的和为,
则阴影部分面积为.
答案为:3.
15.解:如图,过点B作BH⊥AC于点H,
在Rt△ABC中,∠ABC=90°,AB=4,BC=3,
∴AC5,
∵BH⊥AC,
∴S△ABCAC BHAB BC,
∴BH,
在Rt△ABH中,由勾股定理得:AH,
∴CH=AC﹣AH=5,
∵DF⊥AB,EG⊥BC,
∴S△ABDAB DFAD BH,S△BCEBC EGCE BH,
∴AD,CE,
∵BD=BE,BH⊥DE,
∴DH=EH,
∴AH﹣AD=CH﹣CE,
即,
整理得:yx,
即y与x的关系式为yx,
答案为:yx.
三.解答题(共8小题,满分75分)
16.解:(1)23
=433
=4;
(2)
.
17.解:(1)
=2
=2;
(2)
=4.
18.解:(1)由题意得:BF=1.6m,BC=3m,DE=0.6m,
∵BF⊥EF,AE⊥EF,BC⊥AE,
∴四边形BCEF是矩形,
∴CE=BF=1.6m,
∴CD=CE﹣DE=1.6﹣0.6=1(m),
答案为:1.6,3,1;
(2)∵BC⊥AC,
∴∠ACB=90°,
设秋千的长度为x m,
则AB=AD=x m,AC=AD﹣CD=(x﹣1)m,
在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,
即(x﹣1)2+32=x2,
解得:x=5(m),
即秋千的长度是5m;
(3)当BF=2.6m时,CE=2.6m,
∵DE=0.6m,
∴CD=CE﹣DE=2.6﹣0.6=2(m),
由(2)可知,AD=AB=5m,
∴AC=AD﹣CD=5﹣2=3(m),
在Rt△ABC中,由勾股定理得:BC4(m),
即需要将秋千AD往前推送4m,
答案为:4.
19.解:(1)
;
(2)
=4;
(3)∵,
∴,
∵a,b分别是的整数部分和小数部分,
∴a=1,,
∴3a﹣b2.
20.(1)证明:∵S四边形ABCDc2,S梯形AEDC(b+a)b,,S四边形ABCD=S梯形AEDC+S△BED,
∴,
∴,
∴a2+b2=c2;
(2)解:在Rt△ABD中,由勾股定理得AD2=AB2﹣BD2=42﹣x2=16﹣x2,
∵BD+CD=BC=6,
∴CD=BC﹣BD=6﹣x,
在Rt△ACD中,由勾股定理得AD2=AC2﹣CD2=52﹣(6﹣x)2=﹣11+12x﹣x2,
∴16﹣x2=﹣11+12x﹣x2,
∴.
21.解:∵,
∴x=3﹣2,y=3+2,
(1)当x=3﹣2,y=3+2时,
x2﹣3xy+y2=(3﹣2)2﹣3(3﹣2)(3+2)+(3+2)2=9﹣128﹣27+24+9+128=31;
(2)∵x的小数部分为a,y的小数部分为b,
∴a=3﹣2,b=3+25=22,
∴(3﹣222)21+45=44.
22.解:设AE的长为x米,依题意得CE=(AC﹣x)米.
∵AB=DE=2.5,BC=1.5,∠C=90°,
∴AC2,
∵BD=0.5,
在Rt△ECD中,
CE
=1.5.
∴2﹣x=1.5,
∴x=0.5.
即AE=0.5.
答:滑杆顶端A下滑0.5米.
23.解:(1)结论:这个三角形不是“平方倍三角形”.
理由:∵22+()2=25,5×()2=25,
∴22+()2=5×()2,
∴这个三角形是“平方倍三角形”.
(2)设直角边长为a,b,斜边为c,
∵△ABC为“平方倍三角形”.
∴a2+b2=c2,且c2+a2=5b2,
∴2a2+b2=5b2,
∴ba,
∴ca,
∴b:a:c=1::;
(3)在Rt△ABC中,∠ACB=90°,CD为△ABC的中线,
∴AD=CD=DBAB,
∴∠B=∠DCB,∠A=∠DCA,
∵∠A+∠B+∠DCB+∠DCA=180°,
∴∠A+∠B=90°,
∴∠ACB=90°,
∴AB2=AC2+BC2=AC2+16,
∴AC2=AB2﹣16,
∵△BCD是平方倍三角形,
∴当CD2+BD2=5BC2=80,
∴AB2AB2=80,
∴AB2=160,
∴AC12,
∴△ABC的面积AC×BC=24;
当CD2+BC2=5BD2,
∴AB2+16=5AB2,
∴AB2=16=BC2(不合题意舍去),
综上所述:△ABC的面积为24.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
