2025年江苏省南通市中考数学模拟测试题(含答案)
文档属性
| 名称 | 2025年江苏省南通市中考数学模拟测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 07:49:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年江苏省南通市中考数学模拟测试题
一.选择题(共10小题,满分30分,每小题3分)
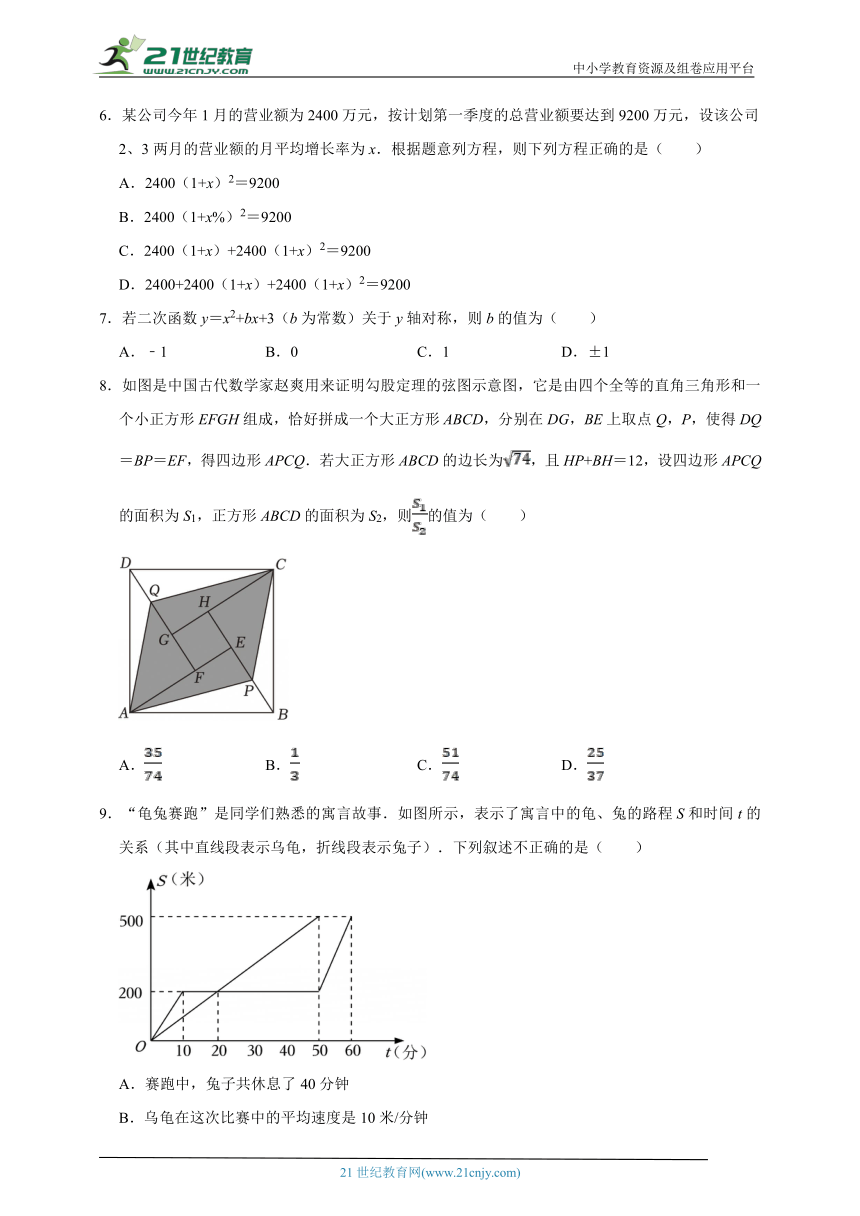
1.早在两千多年前,中国人就开始使用负数,如果收入100元记作+100元,那么支出80元可以记作( )
A.+80元 B.+20元 C.﹣20元 D.﹣80元
2.深圳图书馆北馆是深圳首批建设并完工的新时代重大文化设施,其建筑面积约7.2万平方米,设计藏书量800万册.其中800万用科学记数法表示为( )
A.8×102 B.8×105 C.8×106 D.0.8×107
3.下列计算正确的是( )
A.2
B.42
C.2
D.
4.如图,是某几何体的俯视图,该几何体可能是( )
A. B. C. D.
5.如图,将矩形纸片ABCD沿AC折叠,若∠1=58°,则∠2的大小为( )
A.29° B.32° C.42° D.58°
6.某公司今年1月的营业额为2400万元,按计划第一季度的总营业额要达到9200万元,设该公司2、3两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )
A.2400(1+x)2=9200
B.2400(1+x%)2=9200
C.2400(1+x)+2400(1+x)2=9200
D.2400+2400(1+x)+2400(1+x)2=9200
7.若二次函数y=x2+bx+3(b为常数)关于y轴对称,则b的值为( )
A.﹣1 B.0 C.1 D.±1
8.如图是中国古代数学家赵爽用来证明勾股定理的弦图示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD,分别在DG,BE上取点Q,P,使得DQ=BP=EF,得四边形APCQ.若大正方形ABCD的边长为,且HP+BH=12,设四边形APCQ的面积为S1,正方形ABCD的面积为S2,则的值为( )
A. B. C. D.
9.“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述不正确的是( )
A.赛跑中,兔子共休息了40分钟
B.乌龟在这次比赛中的平均速度是10米/分钟
C.兔子比乌龟早到达终点10分钟
D.兔子休息好后到达终点的平均速度为30米/分钟
10.如图,在△ABC中,AB<AC,将△ABC以点A为中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F.下列结论:①△AFE∽△DFC;②DA平分∠BDE;③∠CDF=∠BAD,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
二.填空题(共8小题,满分30分)
11.因式分解:a3﹣6a2= .
12.如图,一把打开的雨伞(如图1)可近似看成一个圆锥,伞骨(面料下方能够把面料撑起来的支架)末端各点所在圆的直径AC长为120cm,伞骨AB长为90cm(如图2),那么制作这样的一把雨伞至少需要绸布面料 cm2.
13.(4分)关于x的一元二次方程x2﹣4x+1=﹣2k有两个不相等的实数根,则k的取值范围为 .
14.(4分)如图,为了配合疫情工作,浦江某学校门口安装了体温监测仪器,体温检测有效识别区域AB长为6米,当身高为1.5米的学生进入识别区域时,在点B处测得摄像头M的仰角为30°,当学生刚好离开识别区域时,在点A处测得摄像头M的仰角为60°,则学校大门ME的高是 米.
15.(4分)已知菱形的两条对角线长为8cm和6cm,那么这个菱形的面积是 .
16.(4分)老李的鱼菜共生系统内装有恒温装置,如图是某天恒温装置从开启到关闭及关闭后,温度y(℃)与时间x(h)的变化图象,其中AB段是恒温阶段,BC段是恒温系统关闭阶段,是反比例函数图象的一部分,下列说法中:①恒温系统设定的温度为25℃;②k的值为200;③温度在25℃的时间有8h;④恒温系统在一天内保持温度不低于20℃的时间有13h.其中说法正确的是 (填序号).
17.(4分)如图,在正方形ABCD中,O是对角线AC,BD的交点,点E,F分别是边BC,CD延长线上一点,连接OE,OF,EF,OE⊥OF,若∠EOC=30°,,则线段CD的长为 .
18.(4分)一次函数与x轴的交点坐标为 .
三.解答题(共8小题,满分90分)
19.(12分)(1)计算:(m+3)(m﹣3)+m(1﹣m);
(2)解方程:.
20.(10分)为了进一步推进学校安全教育,切实增强广大学生的安全防范意识和自护自救能力,某校举行了安全知识网络竞赛活动,测试满分为100分,为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级抽取了20名参赛学生的成绩.已知抽到的八年级的竞赛成绩(单位:分)如下:80,95,60,80,75,60,95,65,75,70,80,75,85,65,90,70,75,80,85,80.
注:分数在80分以上(不含80分)为优秀.
为了便于分析数据,统计员对八年级的数据进行了整理,得到下表:
成绩等级 分数(单位:分) 学生数
D级 60≤x≤70 a
C级 70<x≤80 9
B级 80<x≤90 b
A级 90<x≤100 2
八、九年级所抽竞赛成绩的平均数、中位数、优秀率如表:
年级 平均数 中位数 优秀率
八年级 77 c 25%
九年级 78.5 82.5 50%
(1)根据题目信息填空:a= ,b= ,c= ;
(2)八年级小明和九年级小亮的分数都为80分,则两位同学在各自年级的排名 更靠前(按照分数由高到低的顺序排序);
(3)若九年级共有700人参加竞赛,请估计九年级80分以上(不含80分)的人数.
21.(10分)如图,已知直线AD与BC相交于点O,OA=OD,OB=OC.求证:AB∥CD.
22.(10分)甲、乙两人用2枚质地均匀的小立方体做游戏(立方体的各个面上标有字母A或字母B),规则为:两人各掷1枚小立方体,当小立方体朝上一面字母相同时,甲获胜;否则乙获胜.
(1)设第1枚小立方体有4个面标有字母A,2个面标有字母B:第2枚小立方体有2个面标有字母A,4个面标有字母B,求甲、乙两人各自获胜的概率.
(2)要使甲、乙两人获胜的概率相同,则第2枚小立方体应有多少面标有字母A?
23.(10分)如图,在△ABC中,∠C=90°,点O是边AB上一点,以点O为圆心,OB为半径作圆,⊙O与AC相切于点D,与BC交于点E,与AB交于点F,连接BD.
(1)求证:BD平分∠ABC;
(2)若BE=2CE,⊙O的半径为4,求图中阴影部分的面积.
24.(12分)某商场的运动服装专柜,对A,B两种品牌的运动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如表.
第一次 第二次
A品牌运动服装数(件) 20 30
B品牌运动服装数(件) 30 40
累计采购款(元) 10200 14400
(1)问A,B两种品牌运动服的进货单价各是多少元?
(2)根据销售情况,商家决定采购B品牌的件数比A品牌件数的倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件A品牌运动服?
25.(13分)【定义】若一个点的纵坐标是横坐标的3倍,则称这个点为“三倍点”,如:A(﹣2,﹣6),B(0,0),C(1,3)等都是“三倍点”.
【背景】已知二次函数y=﹣x2﹣x+c(c为常数),
(1)若记“三倍点”D的横坐标为t,则点D的坐标可表示为 ;
(2)若该函数经过点(1,﹣6);
①求出该函数图象上的“三倍点”坐标;
②在﹣3≤x≤1范围中,记二次函数y=﹣x2﹣x+c的最大值为M,最小值为N,求M﹣N的值;
(3)在﹣3≤x≤1的范围内,若二次函数y=﹣x2﹣x+c的图象上至少存在一个“三倍点”,直接写出c的取值范围.
26.(13分)某数学学习小组在学习了相似三角形以后,他们发现对于同一个物体在灯光下,它的影子的长度与电灯到物体的距离有一定的关系,利用物体影子的长度可以计算电灯到物体的距离,利用电灯到物体的距离也可以计算物体影子的长度.下面是他们的试验内容,请解答:
(1)如图①,放在水平地面上的正方形框架ABCD,在其正上方有一个小射灯P,在小射灯P的照射下,正方形框架在地面上的影子为A′B、D′C,若正方形框架的边长为30cm,A′B=9cm,则△PAD∽△ ;小射灯P离地面的距离为 cm.
(2)如图②,不改变图①中ABCD框架和小射灯P的位置,将另一个同样大小的小正方形框架紧贴在原小正方形框架的左边并排摆放,即正方形ABEF.求小射灯下的影长EF'的长度.
(3)如图③,小射灯P到地面的距离为d,一共有n个边长为a的小正方形框架(无重叠)并排如图摆放,影长A′B与CD'的和为 (用d、n、a表示).
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:“正”和“负”相对,所以,如果收入100元记作+100元,那么支出80元可以记作﹣80元.
故选:D.
2.解:∵800万=8000000,
∴科学记数法表示为:8.0×106,
故选:C.
3.解:A.,故不正确,不符合题意;
B.,故不正确,不符合题意;
C.2,故正确,符合题意;
D.,故不正确,不符合题意.
故选:C.
4.解:圆锥的俯视图是:.
故选:B.
5.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠DAD′=58°,
又∵矩形纸片ABCD沿AC折叠,
∴∠2=∠CAD′,
又∵∠DAD′=∠2+∠CAD′=2∠2=58°,
∴∠2=29°.
故选:A.
6.解:设该公司2、3两月的营业额的月平均增长率为x,
依题意,得:2400+2400(1+x)+2400(1+x)2=9200.
故选:D.
7.解:∴二次函数y=x2+bx+3(b为常数)关于y轴对称,
∴0,
解得b=0.
故选:B.
8.解:设四个全等的直角三角形的两直角边长为a,b(不妨设a<b),
∴DQ=BP=EF=b﹣a,HP=b﹣(b﹣a)=a,
∵正方形ABCD的边长为,
∴a2+b2=74,①
∵HP+BH=12,
∴a+b=12,②
解①②得:a=5,b=7,或a=7,b=5(舍去),
∴PH=CH=5,QG=DG﹣DQ=5﹣(7﹣5)=3,CG=7,EF=7﹣5=2,
∴四边形APCQ的面积为S1=2PH CH+2QG CG+EF2=52+3×7+22=50,
正方形ABCD的面积为S2=74,
∴,
故选:D.
9.解:由图象可得,
赛跑中,兔子共休息了50﹣10=40(分钟),正确,
故选项A不符合题意,
乌龟在这次比赛中的平均速度是500÷50=10(米/分钟),正确,
故选项B不合题意,
乌龟比兔子先到达60﹣50=10(分钟),错误,
故选项C符合题意,
兔子休息好后到达终点的平均速度为:(500﹣200)÷10=30(米/分钟),正确,
故选项D不符合题意,
故选:C.
10.解:∵将△ABC以点A为中心逆时针旋转得到△ADE,
∴∠BAC=∠DAE,∠B=∠ADE,AB=AD,∠E=∠C,
∴∠B=∠ADB,
∴∠ADE=∠ADB,
∴DA平分∠BDE,
∴②符合题意;
∵∠AFE=∠DFC,∠E=∠C,
∴△AFE∽△DFC,
∴①符合题意;
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠FAE,
∵△AFE∽△DFC,
∴∠FAE=∠CDF,
∴∠BAD=∠CDF,
∴③符合题意;
故选:D.
二.填空题(共8小题,满分30分)
11.解:a3﹣6a2=a2(a﹣6).
故答案为:a2(a﹣6).
12.解:∵圆的直径AC长为120cm,
∴圆的周长为120πcm,
∴圆锥的侧面展开图扇形的弧长为120πcm,
∴圆锥的侧面积为:120π×90=5400π(cm2),
∴制作这样的一把雨伞至少需要绸布面料5400πcm2,
故答案为:5400π.
13.解:∵关于x的一元二次方程x2﹣4x+1=﹣2k有两个不相等的实数根,
∴Δ=(﹣4)2﹣4(1+2k)>0且k≠0,
解得k,
故答案为:k.
14.解:根据题意可知,CA=EF=BD=1.5米,CD=AB=6米,
∵∠MCF=60°,∠MDC=30°,
∴∠CMD=∠MCF﹣∠MDC=30°,
∴∠CMD=∠MDC,
∴CM=CD=6米,
在Rt△MCF中,sin∠MCFsin60°,
∴MFCM6=3(米),
∴ME=MF+EF=31.5=(3)(米),
故答案为:(3).
15.解:∵菱形的两条对角线长为8cm和6cm,
∴菱形的面积8×6=24(cm2).
故答案为:24cm2.
16.解:由图象得:AB段是恒温阶段,温度始终保持25℃不变,
∴恒温系统设定的温度为25℃,
故①正确;
把点A(12,25)代入y中得:25,
解得:k=300,
故②不正确;
由图象得:温度在25℃的时间=12﹣8=4(h),
故③正确;
设在升温过程中,温度y与时间x的关系式为:y=ax+b,
把(0,15),(12,25)代入y=ax+b中得:
,
解得:,
∴在升温过程中,温度y与时间x的关系式为:y=2.5x+15,
把y=20代入y=2.5x+15得:20=2.5x+15,
解得:x=2,
把y=20代入y中得:20,
解得:x=15,
∴恒温系统在一天内保持温度不低于20℃的时间=15﹣2=13(h),
故④正确,
综上所述:上列说法中,其中说法正确的是①③④,
故答案为:①③④.
17.解:∵四边形ABCD为正方形,
∴OC=OD,AC⊥BD,∠ADC=∠BCD=90°,
∴∠DCE=∠ADF=90°,
∴∠OCE=∠OCD+∠DCE=135°,∠ODF=∠ODA+∠ADF=135°,
∴∠ODC=45°=∠OCB,
∵AC⊥BD,OE⊥OF,∠EOC=30°,
∴∠EOC+∠EOD=90°,∠EOD+∠FOD=90°,
∴∠EOC=∠FOD=30°,
在△EOC和△FOD中,
,
∴△EOC≌△FOD(ASA),
∴OE=OF,CE=DF,∠OEC=∠OFD,
∴△OEF为等腰直角三角形,
∴∠OFE=∠OEF=45°,
∵∠FOD=30°,∠ODF=135°,
∴∠OFD=180°﹣(∠FOD+∠ODF)=15°,
∴∠CFE=∠OFE﹣∠OFD=45°﹣15°=30°,
在Rt△EFC中,∠CFE=30°,EF,
∴CEEF,
由勾股定理得:FC3,
∵DF=CE,
∴CD=FC﹣DF.
故答案为:.
18.解:将y=0代入y得,
,
解得x=12,
所以一次函数与x轴的交点坐标为(12,0).
故答案为:(12,0).
三.解答题(共8小题,满分90分)
19.解:(1)原式=m2﹣9+m﹣m2
=m﹣9;
(2)解:原方程去分母得:2x=3﹣4(x﹣1),
整理得:2x=7﹣4x,
解得:x,
检验:当x=时,2(x﹣1)≠0,
故原方程的解为x.
20.解:(1)根据频数统计的方法可得,
成绩在60≤x≤70的有6人,即a=6,
成绩在80≤x≤90的有3人,即b=3,
八年级20名学生成绩从小到大排列,处在中间位置的两个数的平均数为77.5(分),因此中位数是77.5,即c=77.5,
故答案为:6,3,77.5;
(2)八年级小明排名靠前,理由:八年级学生成绩的中位数是77.(5分),而九年级学生成绩的中位数是82.5,而八年级小明的得分8(0分)在中位数之上,九年级小亮的得分8(0分)在中位数以下,因此八年级的小明排名靠前;
故答案为:小明;
(3)700×50%=350(人),
答:估计九年级8(0分)以上(不含80分)的人数为350人.
21.证明:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴∠A=∠D,
∴AB∥CD.
22.解:(1)用表格列出所有可能出现的结果:
______ A A B B B B
A (A.A) (A,A) (A,B) (A,B) (A,B) (A,B)
A (A,A) (A,A) (A,B) (A,B) (A,B) (A,B)
A (A,A) (A,A) (A,B) (A,B) (A,B) (A,B)
A (A,A) (A,A) (A,B) (A,B) (A,B) (A,B)
B (B,A) (B,A) (B,B) (B,B) (B,B) (B,B)
B (B,A) (B,A) (B,B) (B,B) (B,B) (B,B)
由表格可知,共有36种可能出现的结果,并且它们可能性是相等的.
”两枚正方体朝上的面所标字母相同”记为事件M,它的发生有16种可能结果,
,
所以甲获胜的概率是;
“两枚正方体朝上的面所标字母不同”记为事件N,它的发生有20种可能结果,
,
所以乙获胜的概率是;
(2)设第二枚正方体有x个面标记为字母A,则有(6﹣x)个面标记字母B,则(A,A)出现的结果数为4x,(B,B)出现的结果数为2(6﹣x),(A,B)出现的结果数为4(6﹣x),(B,A)出现的结果数为2x.
要使两人获胜的概率相等,则P(甲获胜)=P(乙获胜),
P(甲获胜,
解得:x=3.
故要使两人获胜的概率相等,则第二枚正方体要有3个面标记为字母A.
23.解:(1)连接OD,
∵AC与半圆相切于D,
∴OD⊥AC,
∵∠C=90°,
∴BC⊥AC,
∴OD∥BC,
∴∠BDO=∠CBD,
∵OB=OD,
∴∠OBD=∠BDO,
∴∠CBD=∠OBD,
∴BD平分∠ABC.
(2)连接EF,过D作DH⊥BF于H,
∵BF是圆的直径,
∴∠BEF=90°,
∴∠C=∠BEF=90°,
∴BF:AF=BE:CE,
∵BE=2CE,
∴BF=2AF,
∴2OF=2AF,
∴OF=AF,
∴OD=OFAO,
∴sinA,
∴∠A=30°,
∴∠AOD=90°﹣30°=60°,
∵sin∠DOH=sin60°,
∵⊙O的半径为4,
∴OB=OD=4,
∴DH=2,
∴△OBD的面积OB DH4×24,扇形OFD的面积,
∴阴影的面积=△OBD的面积+扇形OFD的面积=4.
24.解:(1)设A品牌运动服装的进货单价是x元,B品牌运动服装的进货单价是y元,依题意得:
,
解得:,
答:A品牌运动服装的进货单价是240元,B品牌运动服装的进货单价是180元;
(2)设购进m件A品牌运动服,则购进(m+5)件B品牌运动服,依题意得:
240m+180(m+5)≤21300,
解得:m≤40,
又m,(m+5)均为整数,
∴m的最大值为40,
答:最多能购进40件A品牌运动服.
25.解:(1)根据定义:若一个点的纵坐标是横坐标的3倍,则称这个点为“三倍点”,可得D(t,3t),
故答案为:(t,3t);
(2)①将点(1,﹣6)代入y=﹣x2﹣x+c,得:﹣6=﹣1﹣1+c,
解得:c=﹣4,
∴y=﹣x2﹣x﹣4,
将(t,3t)代入,得:3t=﹣t2﹣t﹣4,
解得:t1=t2=﹣2,
∴函数y=﹣x2﹣x﹣4图象上的“三倍点”坐标为(﹣2,﹣6);
②∵y=﹣x2﹣x﹣4=﹣(x)2,
∴M,
当x=﹣3时,y=﹣(﹣3)2﹣(﹣3)﹣4=﹣10,
当x=1时,y=﹣1﹣1﹣4=﹣6,
∴N=﹣10,
∴M﹣N(﹣10);
(3)由题意得,三倍点所在的直线为y=3x,
在﹣3≤x≤1的范围内,二次函数y=﹣x2﹣x+c的图象上至少存在一个“三倍点”,
即在﹣3≤x≤1的范围内,二次函数y=﹣x2﹣x+c和y=3x至少有一个交点,
令3x=﹣x2﹣x+c,整理得:x2+4x﹣c=0,
则Δ=b2﹣4ac=16+4c≥0,
解得:c≥﹣4;
把x=﹣3代入y=﹣x2﹣x+c得y=﹣6+c,代入y=3x得y=﹣9,
∴﹣9≥﹣6+c,
解得:c≤﹣3;
把x=1代入y=﹣x2﹣x+c得y=﹣2+c,代入y=3x得y=3,
∴3≥﹣2+c,
解得:c≤5,
综上,c的取值范围为:﹣4≤c≤5.
26.解:(1)如图①,PQ⊥A′D′于点Q,交AD于点R,
∵四边形ABCD是边长为30cm的正方形,
∴AD=AB=BC=30cm,AD∥A′D′,AB⊥A′D′,DC⊥A′D′,
∴△PAD∽△PA′D′,∠PRD=∠PQD′=90°,RQ=AB=30cm,
∴,
∴点P在正方形ABCD的正上方,
∴PA′=PD′,
∴∠A′=∠D′,
∵∠A′BA=∠D′CD=90°,AB=DC,
∴△ABA′≌△DCD′,
∴A′B=D′C=9cm,
∴A′D′=30+9+9=48(cm),
∴,
解得PQ=80,
∴小射灯P离地面的距离为80cm,
故答案为:PA′D′,80.
(2)如图②,PQ⊥A′D′于点Q,交AD于点R,
由(1)得D′C=9cm,RQ=AB=30cm,PQ=80cm,
∴PR=80﹣30=50(cm),
∵AF=BE=BC=AD=30cm,
∴FD=30+30=60(cm),F′D′=EF′+30=30+9=(EF′+69)cm,
∵FD∥F′D′,
∴△PFD∽△PF′D′,
∴,
∴,
解得EF′=27,
答:小射灯下的影长EF'的长度为27cm.
(3)如图③,PQ⊥A′D′于点Q,交AD于点R,则PQ=d,RQ=AB=a,AD=BC=na,
∵AD∥A′D′,
∴△PAD∽△PA′D′,
∴,
∴A′D′,
∴A′B+CD′=A′D′﹣BCna,
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年江苏省南通市中考数学模拟测试题
一.选择题(共10小题,满分30分,每小题3分)
1.早在两千多年前,中国人就开始使用负数,如果收入100元记作+100元,那么支出80元可以记作( )
A.+80元 B.+20元 C.﹣20元 D.﹣80元
2.深圳图书馆北馆是深圳首批建设并完工的新时代重大文化设施,其建筑面积约7.2万平方米,设计藏书量800万册.其中800万用科学记数法表示为( )
A.8×102 B.8×105 C.8×106 D.0.8×107
3.下列计算正确的是( )
A.2
B.42
C.2
D.
4.如图,是某几何体的俯视图,该几何体可能是( )
A. B. C. D.
5.如图,将矩形纸片ABCD沿AC折叠,若∠1=58°,则∠2的大小为( )
A.29° B.32° C.42° D.58°
6.某公司今年1月的营业额为2400万元,按计划第一季度的总营业额要达到9200万元,设该公司2、3两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )
A.2400(1+x)2=9200
B.2400(1+x%)2=9200
C.2400(1+x)+2400(1+x)2=9200
D.2400+2400(1+x)+2400(1+x)2=9200
7.若二次函数y=x2+bx+3(b为常数)关于y轴对称,则b的值为( )
A.﹣1 B.0 C.1 D.±1
8.如图是中国古代数学家赵爽用来证明勾股定理的弦图示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD,分别在DG,BE上取点Q,P,使得DQ=BP=EF,得四边形APCQ.若大正方形ABCD的边长为,且HP+BH=12,设四边形APCQ的面积为S1,正方形ABCD的面积为S2,则的值为( )
A. B. C. D.
9.“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述不正确的是( )
A.赛跑中,兔子共休息了40分钟
B.乌龟在这次比赛中的平均速度是10米/分钟
C.兔子比乌龟早到达终点10分钟
D.兔子休息好后到达终点的平均速度为30米/分钟
10.如图,在△ABC中,AB<AC,将△ABC以点A为中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F.下列结论:①△AFE∽△DFC;②DA平分∠BDE;③∠CDF=∠BAD,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
二.填空题(共8小题,满分30分)
11.因式分解:a3﹣6a2= .
12.如图,一把打开的雨伞(如图1)可近似看成一个圆锥,伞骨(面料下方能够把面料撑起来的支架)末端各点所在圆的直径AC长为120cm,伞骨AB长为90cm(如图2),那么制作这样的一把雨伞至少需要绸布面料 cm2.
13.(4分)关于x的一元二次方程x2﹣4x+1=﹣2k有两个不相等的实数根,则k的取值范围为 .
14.(4分)如图,为了配合疫情工作,浦江某学校门口安装了体温监测仪器,体温检测有效识别区域AB长为6米,当身高为1.5米的学生进入识别区域时,在点B处测得摄像头M的仰角为30°,当学生刚好离开识别区域时,在点A处测得摄像头M的仰角为60°,则学校大门ME的高是 米.
15.(4分)已知菱形的两条对角线长为8cm和6cm,那么这个菱形的面积是 .
16.(4分)老李的鱼菜共生系统内装有恒温装置,如图是某天恒温装置从开启到关闭及关闭后,温度y(℃)与时间x(h)的变化图象,其中AB段是恒温阶段,BC段是恒温系统关闭阶段,是反比例函数图象的一部分,下列说法中:①恒温系统设定的温度为25℃;②k的值为200;③温度在25℃的时间有8h;④恒温系统在一天内保持温度不低于20℃的时间有13h.其中说法正确的是 (填序号).
17.(4分)如图,在正方形ABCD中,O是对角线AC,BD的交点,点E,F分别是边BC,CD延长线上一点,连接OE,OF,EF,OE⊥OF,若∠EOC=30°,,则线段CD的长为 .
18.(4分)一次函数与x轴的交点坐标为 .
三.解答题(共8小题,满分90分)
19.(12分)(1)计算:(m+3)(m﹣3)+m(1﹣m);
(2)解方程:.
20.(10分)为了进一步推进学校安全教育,切实增强广大学生的安全防范意识和自护自救能力,某校举行了安全知识网络竞赛活动,测试满分为100分,为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级抽取了20名参赛学生的成绩.已知抽到的八年级的竞赛成绩(单位:分)如下:80,95,60,80,75,60,95,65,75,70,80,75,85,65,90,70,75,80,85,80.
注:分数在80分以上(不含80分)为优秀.
为了便于分析数据,统计员对八年级的数据进行了整理,得到下表:
成绩等级 分数(单位:分) 学生数
D级 60≤x≤70 a
C级 70<x≤80 9
B级 80<x≤90 b
A级 90<x≤100 2
八、九年级所抽竞赛成绩的平均数、中位数、优秀率如表:
年级 平均数 中位数 优秀率
八年级 77 c 25%
九年级 78.5 82.5 50%
(1)根据题目信息填空:a= ,b= ,c= ;
(2)八年级小明和九年级小亮的分数都为80分,则两位同学在各自年级的排名 更靠前(按照分数由高到低的顺序排序);
(3)若九年级共有700人参加竞赛,请估计九年级80分以上(不含80分)的人数.
21.(10分)如图,已知直线AD与BC相交于点O,OA=OD,OB=OC.求证:AB∥CD.
22.(10分)甲、乙两人用2枚质地均匀的小立方体做游戏(立方体的各个面上标有字母A或字母B),规则为:两人各掷1枚小立方体,当小立方体朝上一面字母相同时,甲获胜;否则乙获胜.
(1)设第1枚小立方体有4个面标有字母A,2个面标有字母B:第2枚小立方体有2个面标有字母A,4个面标有字母B,求甲、乙两人各自获胜的概率.
(2)要使甲、乙两人获胜的概率相同,则第2枚小立方体应有多少面标有字母A?
23.(10分)如图,在△ABC中,∠C=90°,点O是边AB上一点,以点O为圆心,OB为半径作圆,⊙O与AC相切于点D,与BC交于点E,与AB交于点F,连接BD.
(1)求证:BD平分∠ABC;
(2)若BE=2CE,⊙O的半径为4,求图中阴影部分的面积.
24.(12分)某商场的运动服装专柜,对A,B两种品牌的运动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如表.
第一次 第二次
A品牌运动服装数(件) 20 30
B品牌运动服装数(件) 30 40
累计采购款(元) 10200 14400
(1)问A,B两种品牌运动服的进货单价各是多少元?
(2)根据销售情况,商家决定采购B品牌的件数比A品牌件数的倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件A品牌运动服?
25.(13分)【定义】若一个点的纵坐标是横坐标的3倍,则称这个点为“三倍点”,如:A(﹣2,﹣6),B(0,0),C(1,3)等都是“三倍点”.
【背景】已知二次函数y=﹣x2﹣x+c(c为常数),
(1)若记“三倍点”D的横坐标为t,则点D的坐标可表示为 ;
(2)若该函数经过点(1,﹣6);
①求出该函数图象上的“三倍点”坐标;
②在﹣3≤x≤1范围中,记二次函数y=﹣x2﹣x+c的最大值为M,最小值为N,求M﹣N的值;
(3)在﹣3≤x≤1的范围内,若二次函数y=﹣x2﹣x+c的图象上至少存在一个“三倍点”,直接写出c的取值范围.
26.(13分)某数学学习小组在学习了相似三角形以后,他们发现对于同一个物体在灯光下,它的影子的长度与电灯到物体的距离有一定的关系,利用物体影子的长度可以计算电灯到物体的距离,利用电灯到物体的距离也可以计算物体影子的长度.下面是他们的试验内容,请解答:
(1)如图①,放在水平地面上的正方形框架ABCD,在其正上方有一个小射灯P,在小射灯P的照射下,正方形框架在地面上的影子为A′B、D′C,若正方形框架的边长为30cm,A′B=9cm,则△PAD∽△ ;小射灯P离地面的距离为 cm.
(2)如图②,不改变图①中ABCD框架和小射灯P的位置,将另一个同样大小的小正方形框架紧贴在原小正方形框架的左边并排摆放,即正方形ABEF.求小射灯下的影长EF'的长度.
(3)如图③,小射灯P到地面的距离为d,一共有n个边长为a的小正方形框架(无重叠)并排如图摆放,影长A′B与CD'的和为 (用d、n、a表示).
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:“正”和“负”相对,所以,如果收入100元记作+100元,那么支出80元可以记作﹣80元.
故选:D.
2.解:∵800万=8000000,
∴科学记数法表示为:8.0×106,
故选:C.
3.解:A.,故不正确,不符合题意;
B.,故不正确,不符合题意;
C.2,故正确,符合题意;
D.,故不正确,不符合题意.
故选:C.
4.解:圆锥的俯视图是:.
故选:B.
5.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠DAD′=58°,
又∵矩形纸片ABCD沿AC折叠,
∴∠2=∠CAD′,
又∵∠DAD′=∠2+∠CAD′=2∠2=58°,
∴∠2=29°.
故选:A.
6.解:设该公司2、3两月的营业额的月平均增长率为x,
依题意,得:2400+2400(1+x)+2400(1+x)2=9200.
故选:D.
7.解:∴二次函数y=x2+bx+3(b为常数)关于y轴对称,
∴0,
解得b=0.
故选:B.
8.解:设四个全等的直角三角形的两直角边长为a,b(不妨设a<b),
∴DQ=BP=EF=b﹣a,HP=b﹣(b﹣a)=a,
∵正方形ABCD的边长为,
∴a2+b2=74,①
∵HP+BH=12,
∴a+b=12,②
解①②得:a=5,b=7,或a=7,b=5(舍去),
∴PH=CH=5,QG=DG﹣DQ=5﹣(7﹣5)=3,CG=7,EF=7﹣5=2,
∴四边形APCQ的面积为S1=2PH CH+2QG CG+EF2=52+3×7+22=50,
正方形ABCD的面积为S2=74,
∴,
故选:D.
9.解:由图象可得,
赛跑中,兔子共休息了50﹣10=40(分钟),正确,
故选项A不符合题意,
乌龟在这次比赛中的平均速度是500÷50=10(米/分钟),正确,
故选项B不合题意,
乌龟比兔子先到达60﹣50=10(分钟),错误,
故选项C符合题意,
兔子休息好后到达终点的平均速度为:(500﹣200)÷10=30(米/分钟),正确,
故选项D不符合题意,
故选:C.
10.解:∵将△ABC以点A为中心逆时针旋转得到△ADE,
∴∠BAC=∠DAE,∠B=∠ADE,AB=AD,∠E=∠C,
∴∠B=∠ADB,
∴∠ADE=∠ADB,
∴DA平分∠BDE,
∴②符合题意;
∵∠AFE=∠DFC,∠E=∠C,
∴△AFE∽△DFC,
∴①符合题意;
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠FAE,
∵△AFE∽△DFC,
∴∠FAE=∠CDF,
∴∠BAD=∠CDF,
∴③符合题意;
故选:D.
二.填空题(共8小题,满分30分)
11.解:a3﹣6a2=a2(a﹣6).
故答案为:a2(a﹣6).
12.解:∵圆的直径AC长为120cm,
∴圆的周长为120πcm,
∴圆锥的侧面展开图扇形的弧长为120πcm,
∴圆锥的侧面积为:120π×90=5400π(cm2),
∴制作这样的一把雨伞至少需要绸布面料5400πcm2,
故答案为:5400π.
13.解:∵关于x的一元二次方程x2﹣4x+1=﹣2k有两个不相等的实数根,
∴Δ=(﹣4)2﹣4(1+2k)>0且k≠0,
解得k,
故答案为:k.
14.解:根据题意可知,CA=EF=BD=1.5米,CD=AB=6米,
∵∠MCF=60°,∠MDC=30°,
∴∠CMD=∠MCF﹣∠MDC=30°,
∴∠CMD=∠MDC,
∴CM=CD=6米,
在Rt△MCF中,sin∠MCFsin60°,
∴MFCM6=3(米),
∴ME=MF+EF=31.5=(3)(米),
故答案为:(3).
15.解:∵菱形的两条对角线长为8cm和6cm,
∴菱形的面积8×6=24(cm2).
故答案为:24cm2.
16.解:由图象得:AB段是恒温阶段,温度始终保持25℃不变,
∴恒温系统设定的温度为25℃,
故①正确;
把点A(12,25)代入y中得:25,
解得:k=300,
故②不正确;
由图象得:温度在25℃的时间=12﹣8=4(h),
故③正确;
设在升温过程中,温度y与时间x的关系式为:y=ax+b,
把(0,15),(12,25)代入y=ax+b中得:
,
解得:,
∴在升温过程中,温度y与时间x的关系式为:y=2.5x+15,
把y=20代入y=2.5x+15得:20=2.5x+15,
解得:x=2,
把y=20代入y中得:20,
解得:x=15,
∴恒温系统在一天内保持温度不低于20℃的时间=15﹣2=13(h),
故④正确,
综上所述:上列说法中,其中说法正确的是①③④,
故答案为:①③④.
17.解:∵四边形ABCD为正方形,
∴OC=OD,AC⊥BD,∠ADC=∠BCD=90°,
∴∠DCE=∠ADF=90°,
∴∠OCE=∠OCD+∠DCE=135°,∠ODF=∠ODA+∠ADF=135°,
∴∠ODC=45°=∠OCB,
∵AC⊥BD,OE⊥OF,∠EOC=30°,
∴∠EOC+∠EOD=90°,∠EOD+∠FOD=90°,
∴∠EOC=∠FOD=30°,
在△EOC和△FOD中,
,
∴△EOC≌△FOD(ASA),
∴OE=OF,CE=DF,∠OEC=∠OFD,
∴△OEF为等腰直角三角形,
∴∠OFE=∠OEF=45°,
∵∠FOD=30°,∠ODF=135°,
∴∠OFD=180°﹣(∠FOD+∠ODF)=15°,
∴∠CFE=∠OFE﹣∠OFD=45°﹣15°=30°,
在Rt△EFC中,∠CFE=30°,EF,
∴CEEF,
由勾股定理得:FC3,
∵DF=CE,
∴CD=FC﹣DF.
故答案为:.
18.解:将y=0代入y得,
,
解得x=12,
所以一次函数与x轴的交点坐标为(12,0).
故答案为:(12,0).
三.解答题(共8小题,满分90分)
19.解:(1)原式=m2﹣9+m﹣m2
=m﹣9;
(2)解:原方程去分母得:2x=3﹣4(x﹣1),
整理得:2x=7﹣4x,
解得:x,
检验:当x=时,2(x﹣1)≠0,
故原方程的解为x.
20.解:(1)根据频数统计的方法可得,
成绩在60≤x≤70的有6人,即a=6,
成绩在80≤x≤90的有3人,即b=3,
八年级20名学生成绩从小到大排列,处在中间位置的两个数的平均数为77.5(分),因此中位数是77.5,即c=77.5,
故答案为:6,3,77.5;
(2)八年级小明排名靠前,理由:八年级学生成绩的中位数是77.(5分),而九年级学生成绩的中位数是82.5,而八年级小明的得分8(0分)在中位数之上,九年级小亮的得分8(0分)在中位数以下,因此八年级的小明排名靠前;
故答案为:小明;
(3)700×50%=350(人),
答:估计九年级8(0分)以上(不含80分)的人数为350人.
21.证明:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴∠A=∠D,
∴AB∥CD.
22.解:(1)用表格列出所有可能出现的结果:
______ A A B B B B
A (A.A) (A,A) (A,B) (A,B) (A,B) (A,B)
A (A,A) (A,A) (A,B) (A,B) (A,B) (A,B)
A (A,A) (A,A) (A,B) (A,B) (A,B) (A,B)
A (A,A) (A,A) (A,B) (A,B) (A,B) (A,B)
B (B,A) (B,A) (B,B) (B,B) (B,B) (B,B)
B (B,A) (B,A) (B,B) (B,B) (B,B) (B,B)
由表格可知,共有36种可能出现的结果,并且它们可能性是相等的.
”两枚正方体朝上的面所标字母相同”记为事件M,它的发生有16种可能结果,
,
所以甲获胜的概率是;
“两枚正方体朝上的面所标字母不同”记为事件N,它的发生有20种可能结果,
,
所以乙获胜的概率是;
(2)设第二枚正方体有x个面标记为字母A,则有(6﹣x)个面标记字母B,则(A,A)出现的结果数为4x,(B,B)出现的结果数为2(6﹣x),(A,B)出现的结果数为4(6﹣x),(B,A)出现的结果数为2x.
要使两人获胜的概率相等,则P(甲获胜)=P(乙获胜),
P(甲获胜,
解得:x=3.
故要使两人获胜的概率相等,则第二枚正方体要有3个面标记为字母A.
23.解:(1)连接OD,
∵AC与半圆相切于D,
∴OD⊥AC,
∵∠C=90°,
∴BC⊥AC,
∴OD∥BC,
∴∠BDO=∠CBD,
∵OB=OD,
∴∠OBD=∠BDO,
∴∠CBD=∠OBD,
∴BD平分∠ABC.
(2)连接EF,过D作DH⊥BF于H,
∵BF是圆的直径,
∴∠BEF=90°,
∴∠C=∠BEF=90°,
∴BF:AF=BE:CE,
∵BE=2CE,
∴BF=2AF,
∴2OF=2AF,
∴OF=AF,
∴OD=OFAO,
∴sinA,
∴∠A=30°,
∴∠AOD=90°﹣30°=60°,
∵sin∠DOH=sin60°,
∵⊙O的半径为4,
∴OB=OD=4,
∴DH=2,
∴△OBD的面积OB DH4×24,扇形OFD的面积,
∴阴影的面积=△OBD的面积+扇形OFD的面积=4.
24.解:(1)设A品牌运动服装的进货单价是x元,B品牌运动服装的进货单价是y元,依题意得:
,
解得:,
答:A品牌运动服装的进货单价是240元,B品牌运动服装的进货单价是180元;
(2)设购进m件A品牌运动服,则购进(m+5)件B品牌运动服,依题意得:
240m+180(m+5)≤21300,
解得:m≤40,
又m,(m+5)均为整数,
∴m的最大值为40,
答:最多能购进40件A品牌运动服.
25.解:(1)根据定义:若一个点的纵坐标是横坐标的3倍,则称这个点为“三倍点”,可得D(t,3t),
故答案为:(t,3t);
(2)①将点(1,﹣6)代入y=﹣x2﹣x+c,得:﹣6=﹣1﹣1+c,
解得:c=﹣4,
∴y=﹣x2﹣x﹣4,
将(t,3t)代入,得:3t=﹣t2﹣t﹣4,
解得:t1=t2=﹣2,
∴函数y=﹣x2﹣x﹣4图象上的“三倍点”坐标为(﹣2,﹣6);
②∵y=﹣x2﹣x﹣4=﹣(x)2,
∴M,
当x=﹣3时,y=﹣(﹣3)2﹣(﹣3)﹣4=﹣10,
当x=1时,y=﹣1﹣1﹣4=﹣6,
∴N=﹣10,
∴M﹣N(﹣10);
(3)由题意得,三倍点所在的直线为y=3x,
在﹣3≤x≤1的范围内,二次函数y=﹣x2﹣x+c的图象上至少存在一个“三倍点”,
即在﹣3≤x≤1的范围内,二次函数y=﹣x2﹣x+c和y=3x至少有一个交点,
令3x=﹣x2﹣x+c,整理得:x2+4x﹣c=0,
则Δ=b2﹣4ac=16+4c≥0,
解得:c≥﹣4;
把x=﹣3代入y=﹣x2﹣x+c得y=﹣6+c,代入y=3x得y=﹣9,
∴﹣9≥﹣6+c,
解得:c≤﹣3;
把x=1代入y=﹣x2﹣x+c得y=﹣2+c,代入y=3x得y=3,
∴3≥﹣2+c,
解得:c≤5,
综上,c的取值范围为:﹣4≤c≤5.
26.解:(1)如图①,PQ⊥A′D′于点Q,交AD于点R,
∵四边形ABCD是边长为30cm的正方形,
∴AD=AB=BC=30cm,AD∥A′D′,AB⊥A′D′,DC⊥A′D′,
∴△PAD∽△PA′D′,∠PRD=∠PQD′=90°,RQ=AB=30cm,
∴,
∴点P在正方形ABCD的正上方,
∴PA′=PD′,
∴∠A′=∠D′,
∵∠A′BA=∠D′CD=90°,AB=DC,
∴△ABA′≌△DCD′,
∴A′B=D′C=9cm,
∴A′D′=30+9+9=48(cm),
∴,
解得PQ=80,
∴小射灯P离地面的距离为80cm,
故答案为:PA′D′,80.
(2)如图②,PQ⊥A′D′于点Q,交AD于点R,
由(1)得D′C=9cm,RQ=AB=30cm,PQ=80cm,
∴PR=80﹣30=50(cm),
∵AF=BE=BC=AD=30cm,
∴FD=30+30=60(cm),F′D′=EF′+30=30+9=(EF′+69)cm,
∵FD∥F′D′,
∴△PFD∽△PF′D′,
∴,
∴,
解得EF′=27,
答:小射灯下的影长EF'的长度为27cm.
(3)如图③,PQ⊥A′D′于点Q,交AD于点R,则PQ=d,RQ=AB=a,AD=BC=na,
∵AD∥A′D′,
∴△PAD∽△PA′D′,
∴,
∴A′D′,
∴A′B+CD′=A′D′﹣BCna,
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
