人教版八年级数学下册 18.1.2 平行四边形的判定同步测试(含解析)
文档属性
| 名称 | 人教版八年级数学下册 18.1.2 平行四边形的判定同步测试(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 807.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 15:31:56 | ||
图片预览

文档简介
18.1.2 平行四边形的判定
一、单选题
1.如图,平行四边形ABCD的对角线交于点,下列结论一定成立的是( )
A. B. C. D.
2.如图,在四边形中, ,若添加一个条件,使四边形为平形四边形,则下列正确的是( )
A. B. C. D.
3.如图,在平行四边形ABCD中,对角线与相交于点,则下列结论一定正确的是( )
A. B. C. D.
4.将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )
A.100° B.80° C.70° D.60°
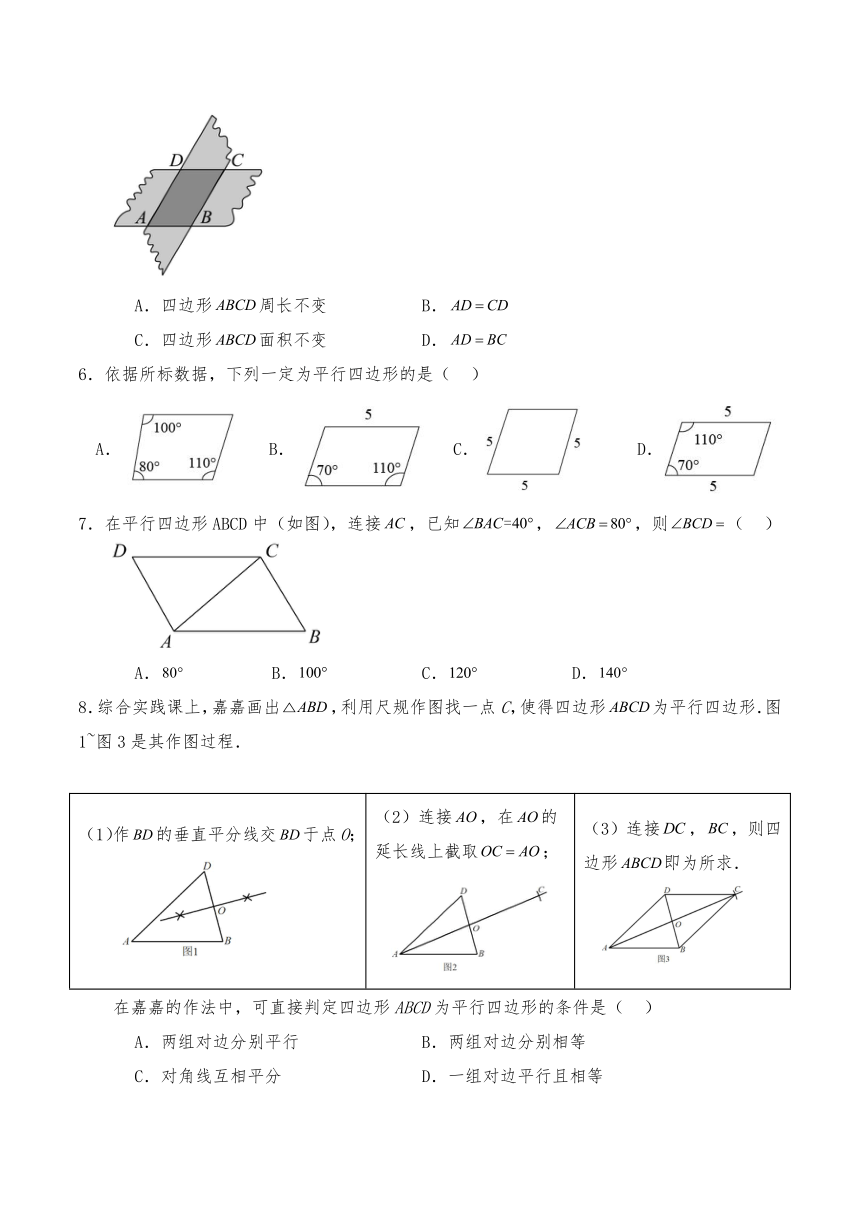
5.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形周长不变 B.
C.四边形面积不变 D.
6.依据所标数据,下列一定为平行四边形的是( )
A. B. C. D.
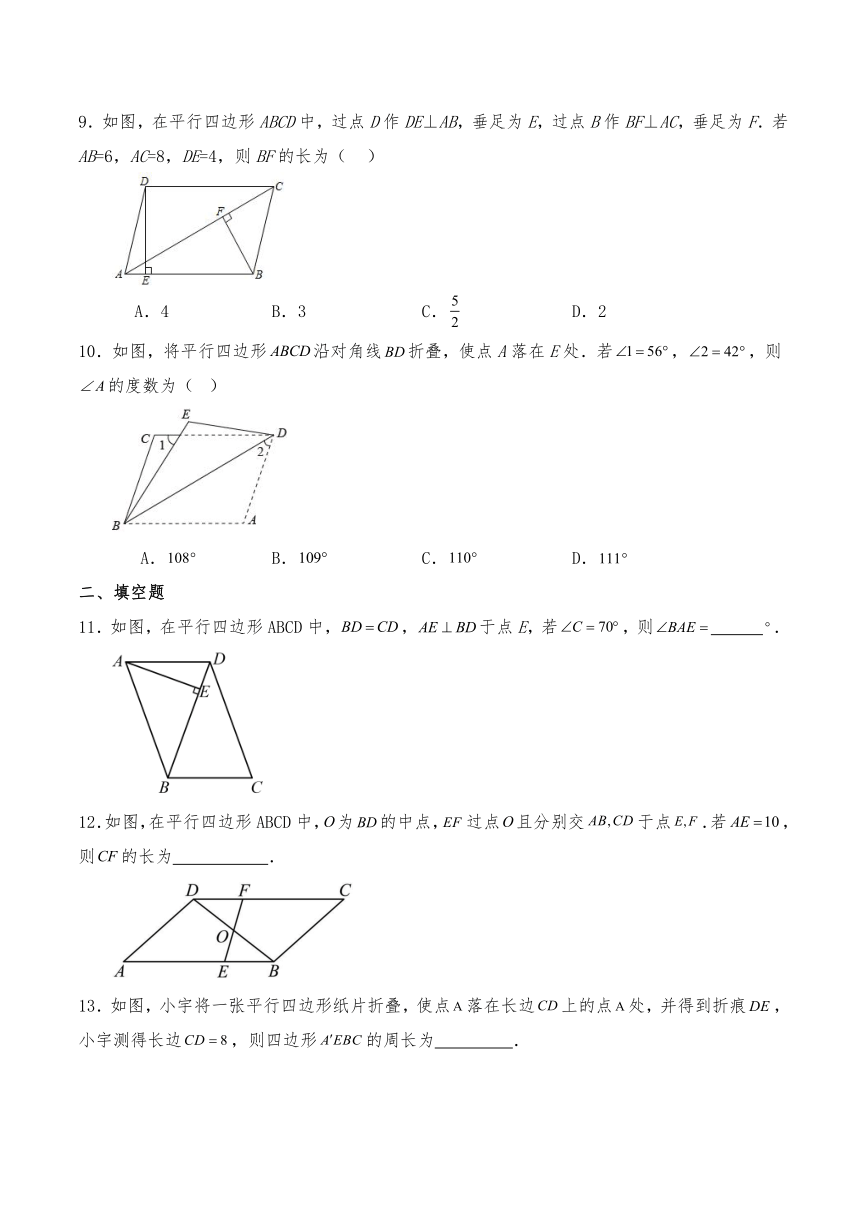
7.在平行四边形ABCD中(如图),连接,已知,,则( )
A. B. C. D.
8.综合实践课上,嘉嘉画出,利用尺规作图找一点C,使得四边形为平行四边形.图1~图3是其作图过程.
(1)作的垂直平分线交于点O; (2)连接,在的延长线上截取; (3)连接,,则四边形即为所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
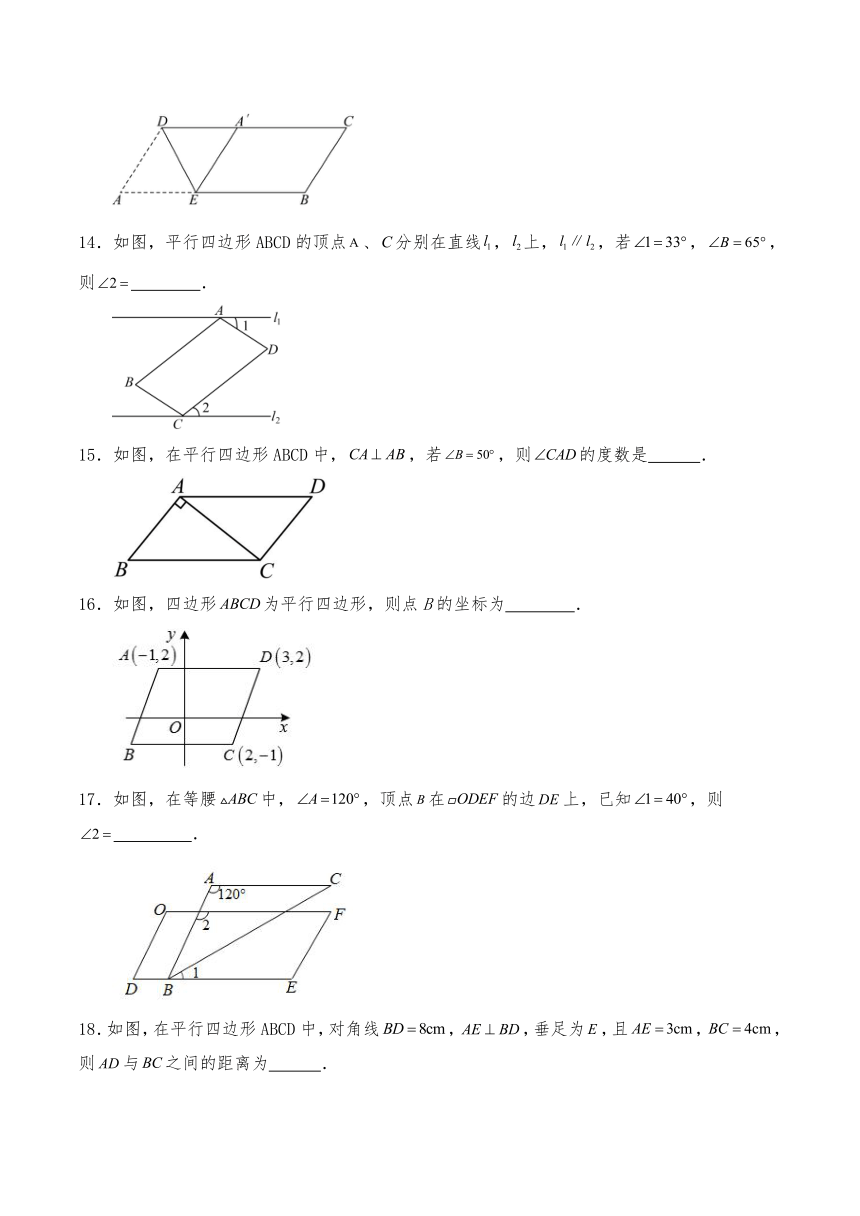
9.如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A.4 B.3 C. D.2
10.如图,将平行四边形沿对角线折叠,使点A落在E处.若,,则的度数为( )
A. B. C. D.
二、填空题
11.如图,在平行四边形ABCD中,,于点E,若,则 .
12.如图,在平行四边形ABCD中,为的中点,过点且分别交于点.若,则的长为 .
13.如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕,小宇测得长边,则四边形的周长为 .
14.如图,平行四边形ABCD的顶点、分别在直线,上,,若,,则 .
15.如图,在平行四边形ABCD中,,若,则的度数是 .
16.如图,四边形为平行四边形,则点B的坐标为 .
17.如图,在等腰中,,顶点在的边上,已知,则 .
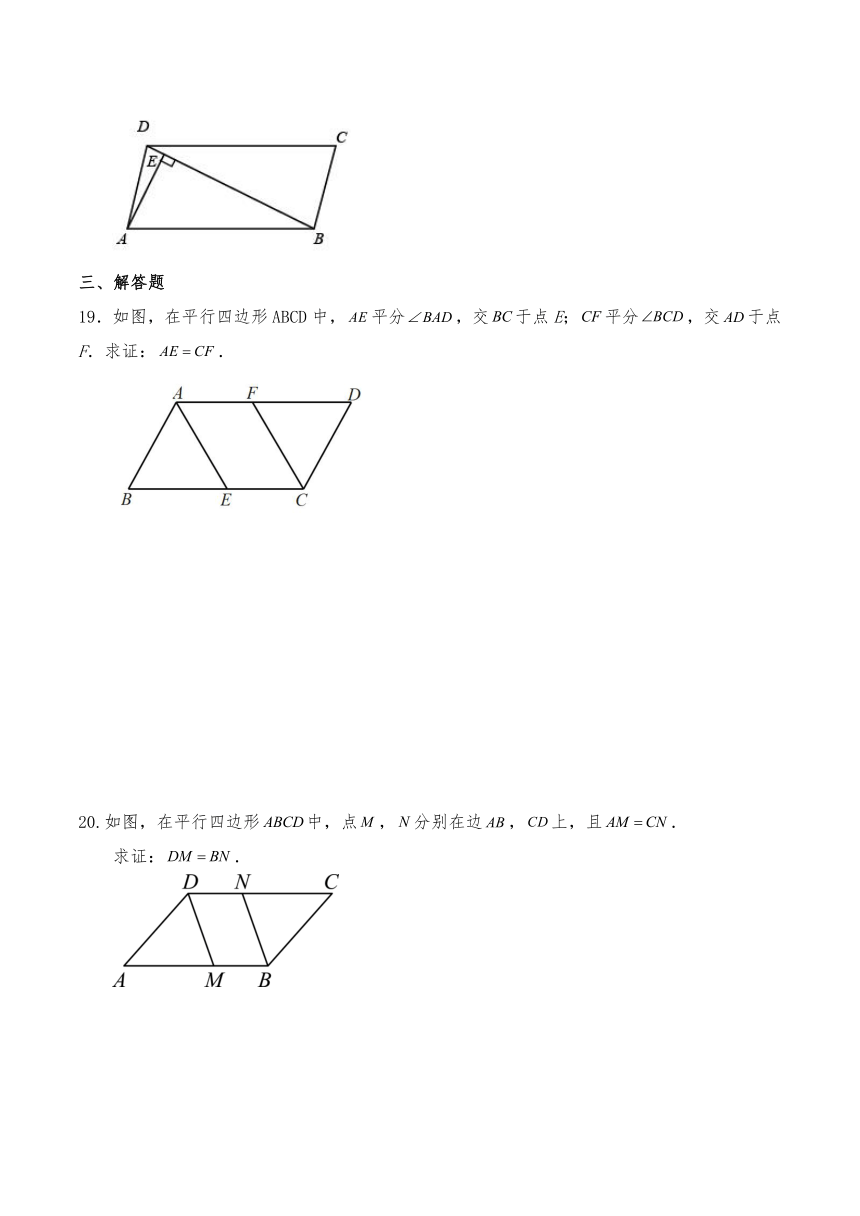
18.如图,在平行四边形ABCD中,对角线,,垂足为,且,,则与之间的距离为 .
三、解答题
19.如图,在平行四边形ABCD中,平分,交于点E;平分,交于点F.求证:.
20.如图,在平行四边形中,点,分别在边,上,且.
求证:.
21.如图,在四边形中,与交于点,,垂足分别为点,且.求证:四边形是平行四边形.
22.如图,是的一个外角,,.
(1)尺规作图:作的平分线,交于点D(保留作图痕迹,不写作法);
(2)求证:四边形是平行四边形.
23.在中,点D,F分别为边AC,AB的中点.延长DF到点E,使,连接BE.
(1)求证:; (2)求证:四边形BCDE是平行四边形.
24.如图,平行四边形的对角线相交于点,点在对角线上,且,连接,.
(1)求证:四边形是平行四边形.
(2)若的面积等于2,求的面积.
答案:
一、单选题
1.C
【分析】根据平行四边形性质逐项验证即可得到答案.
解:A、根据平行四边形性质:对角线相互平分,在中,,,则不一定成立,该选项不符合题意;
B、根据平行四边形性质:对角线相互平分,不一定垂直,则不一定成立,该选项不符合题意;
C、根据平行四边形性质:对角线相互平分,在中,,该选项符合题意;
D、根据平行四边形性质,对角线不一定平分对角,则不一定成立,该选项不符合题意;
故选:C.
2.D
【分析】根据平行四边形的判定定理逐项分析判断即可求解.
解:A.根据,,不能判断四边形为平形四边形,故该选项不正确,不符合题意;
B. ∵,∴,不能判断四边形为平形四边形,故该选项不正确,不符合题意;
C.根据,,不能判断四边形为平形四边形,故该选项不正确,不符合题意;
D.∵,
∴,
∵
∴,
∴
∴四边形为平形四边形,
故该选项正确,符合题意;
故选:D.
3.B
【分析】根据平行四边形的性质逐项分析判断即可求解.
解:∵四边形是平行四边形,对角线与相交于点,
A. ,不一定成立,故该选项不正确,不符合题意;
B. ,故该选项正确,符合题意;
C. ,不一定成立,故该选项不正确,不符合题意;
D. ,不一定成立,故该选项不正确,不符合题意;
故选:B.
4.B
【分析】由平行四边形的性质可得AB∥DC,再根据三角形内角和定理,即可得到∠GEF的度数,依据平行线的性质,即可得到∠EGC的度数.
解:∵四边形ABCD是平行四边形,
∴,
∴∠AEG=∠EGC,
∵∠EFG=90°,∠EGF=60°,
∴∠GEF=30°,
∴∠GEA=80°,
∴∠EGC=80°.
故选:B.
5.D
【分析】由平行四边形的性质进行判断,即可得到答案.
解:由题意可知,
∵,,
∴四边形是平行四边形,
∴;故D符合题意;
随着一张纸条在转动过程中,不一定等于,四边形周长、面积都会改变;故A、B、C不符合题意;
故选:D
6.D
【分析】根据平行四边形的判定及性质定理判断即可;
解:平行四边形对角相等,故A错误;
一组对边平行不能判断四边形是平行四边形,故B错误;
三边相等不能判断四边形是平行四边形,故C错误;
一组对边平行且相等的四边形是平行四边形,故D正确;
故选:D.
7.C
【分析】根据平行四边形的对边平行和两直线平行内错角相等的性质,再通过等量代换即可求解.
解:∵四边形ABCD为平行四边形,
∴ABCD
∴∠DCA=∠CAB,
∵∠DCA+∠ACB,,
∴40 +80 =120 ,
故选:C.
8.C
【分析】根据作图步骤可知,得出了对角线互相平分,从而可以判断.
解:根据图1,得出的中点,图2,得出,
可知使得对角线互相平分,从而得出四边形为平行四边形,
判定四边形ABCD为平行四边形的条件是:对角线互相平分,
故选:C.
9.B
【分析】利用平行四边形ABCD的面积公式即可求解.
解:∵DE⊥AB,BF⊥AC,
∴S平行四边形ABCD=DE×AB=2××AC×BF,
∴4×6=2××8×BF,
∴BF=3,
故选:B.
10.C
【分析】先根据平行四边形的性质,得出,根据平行线的性质,得出,根据折叠得出,根据三角形内角和得出∠A的度数即可.
解:∵四边形ABCD为平行四边形,
∴,
,
根据折叠可知,,
∴,
,
∴,故C正确.
故选:C.
二、填空题
11.
【分析】证明,,由,可得,结合,可得.
解:∵,,
∴,,
∵平行四边形ABCD,
∴,
∴,
∵,
∴;
故答案为:
12.10
【分析】由平行四边形的性质可得即,再结合可得可得,最进一步说明即可解答.
解:∵中,
∴,
∴,
∵,
∴,
∴,
∴,即.
故答案为:10.
13.
【分析】可证,从而可得,再证四边形是平行四边形,可得,即可求解.
解:四边形是平行四边形,
,
,
由折叠得:,
,,
,
,
,
,
,
四边形是平行四边形,
.
故答案:.
14.
【分析】根据平行四边形的性质得到,再利用平行线的性质得到即可解答.
解:过点作,
∴
∵,
∴,
∴,
∴,
∵在平行四边形ABCD中,
∴,
∵,
∴,
∵,
∴,
故答案为:.
15.
【分析】根据平行四边形对边平行可得,利用平行线的性质可得,因此利用直角三角形两个锐角互余求出即可.
解:∵四边形是平行四边形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
故答案为:.
16.
【分析】根据平行四边形的性质以及点的平移即可得出结论.
解:四边形为平行四边形,
,即将点平移到的过程与将点平移到的过程保持一致,
将点平移到的过程是:(向左平移4各单位长度);(上下无平移);
将点平移到的过程按照上述一致过程进行得到,即,
故答案为:.
17.110
【分析】先根据等腰三角形的性质求出∠ABC的度数;再根据平行四边形对边平行和两直线平行同旁内角互补的性质,得出∠2+∠ABE=180 ,代入求解即可.
解:∵是等腰三角形,∠A=120 ,
∴∠ABC=∠C=(180 -∠A)÷2=30 ,
∵四边形是平行四边形,
∴OFDE,
∴∠2+∠ABE=180 ,
即∠2+30 +40 =180 ,
∴∠2=110 .
故答案为:110 .
18..
【分析】设与之间的距离为,由条件可知的面积是的面积的2倍,可求得的面积,,因此可求得的长.
解:∵四边形为平行四边形,
∴,,
,
∴,
∵,,,
∴,
∴,
设与之间的距离为,
∵,
∴,
∴,
解得,
故答案为:.
三、解答题
19.
解:证明:∵四边形是平行四边形,
∴,,,,
∵平分,平分,
∴,
在和中,
∴
∴.
20.
解:证明:∵四边形是平行四边形,
∴,,
∵,
∴,即,
又∵,
∴四边形是平行四边形,
∴.
21.
解:证明:,,
,
又,
,
,
∵,
,
四边形是平行四边形.
22.
(1)解:如图,为所作;
(2)证明:,
,
平分,
,
,
即,
,
,
,
四边形是平行四边形.
23.
解:(1)证明:∵点F为边AB的中点,
∴,
在与中,
,
∴;
(2)证明:∵点D为边AC的中点,
∴,
由(1)得,
∴,,
∴,,
∴四边形BCDE是平行四边形.
24.
解:(1)证明:四边形是平行四边形,
,,
,
,
,
又,
四边形是平行四边形.
(2)解:,,
∴S AEF=S ABE=2
四边形是平行四边形,
∴S CFO=S CEF=S AEF=×2=1
一、单选题
1.如图,平行四边形ABCD的对角线交于点,下列结论一定成立的是( )
A. B. C. D.
2.如图,在四边形中, ,若添加一个条件,使四边形为平形四边形,则下列正确的是( )
A. B. C. D.
3.如图,在平行四边形ABCD中,对角线与相交于点,则下列结论一定正确的是( )
A. B. C. D.
4.将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )
A.100° B.80° C.70° D.60°
5.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形周长不变 B.
C.四边形面积不变 D.
6.依据所标数据,下列一定为平行四边形的是( )
A. B. C. D.
7.在平行四边形ABCD中(如图),连接,已知,,则( )
A. B. C. D.
8.综合实践课上,嘉嘉画出,利用尺规作图找一点C,使得四边形为平行四边形.图1~图3是其作图过程.
(1)作的垂直平分线交于点O; (2)连接,在的延长线上截取; (3)连接,,则四边形即为所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
9.如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A.4 B.3 C. D.2
10.如图,将平行四边形沿对角线折叠,使点A落在E处.若,,则的度数为( )
A. B. C. D.
二、填空题
11.如图,在平行四边形ABCD中,,于点E,若,则 .
12.如图,在平行四边形ABCD中,为的中点,过点且分别交于点.若,则的长为 .
13.如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕,小宇测得长边,则四边形的周长为 .
14.如图,平行四边形ABCD的顶点、分别在直线,上,,若,,则 .
15.如图,在平行四边形ABCD中,,若,则的度数是 .
16.如图,四边形为平行四边形,则点B的坐标为 .
17.如图,在等腰中,,顶点在的边上,已知,则 .
18.如图,在平行四边形ABCD中,对角线,,垂足为,且,,则与之间的距离为 .
三、解答题
19.如图,在平行四边形ABCD中,平分,交于点E;平分,交于点F.求证:.
20.如图,在平行四边形中,点,分别在边,上,且.
求证:.
21.如图,在四边形中,与交于点,,垂足分别为点,且.求证:四边形是平行四边形.
22.如图,是的一个外角,,.
(1)尺规作图:作的平分线,交于点D(保留作图痕迹,不写作法);
(2)求证:四边形是平行四边形.
23.在中,点D,F分别为边AC,AB的中点.延长DF到点E,使,连接BE.
(1)求证:; (2)求证:四边形BCDE是平行四边形.
24.如图,平行四边形的对角线相交于点,点在对角线上,且,连接,.
(1)求证:四边形是平行四边形.
(2)若的面积等于2,求的面积.
答案:
一、单选题
1.C
【分析】根据平行四边形性质逐项验证即可得到答案.
解:A、根据平行四边形性质:对角线相互平分,在中,,,则不一定成立,该选项不符合题意;
B、根据平行四边形性质:对角线相互平分,不一定垂直,则不一定成立,该选项不符合题意;
C、根据平行四边形性质:对角线相互平分,在中,,该选项符合题意;
D、根据平行四边形性质,对角线不一定平分对角,则不一定成立,该选项不符合题意;
故选:C.
2.D
【分析】根据平行四边形的判定定理逐项分析判断即可求解.
解:A.根据,,不能判断四边形为平形四边形,故该选项不正确,不符合题意;
B. ∵,∴,不能判断四边形为平形四边形,故该选项不正确,不符合题意;
C.根据,,不能判断四边形为平形四边形,故该选项不正确,不符合题意;
D.∵,
∴,
∵
∴,
∴
∴四边形为平形四边形,
故该选项正确,符合题意;
故选:D.
3.B
【分析】根据平行四边形的性质逐项分析判断即可求解.
解:∵四边形是平行四边形,对角线与相交于点,
A. ,不一定成立,故该选项不正确,不符合题意;
B. ,故该选项正确,符合题意;
C. ,不一定成立,故该选项不正确,不符合题意;
D. ,不一定成立,故该选项不正确,不符合题意;
故选:B.
4.B
【分析】由平行四边形的性质可得AB∥DC,再根据三角形内角和定理,即可得到∠GEF的度数,依据平行线的性质,即可得到∠EGC的度数.
解:∵四边形ABCD是平行四边形,
∴,
∴∠AEG=∠EGC,
∵∠EFG=90°,∠EGF=60°,
∴∠GEF=30°,
∴∠GEA=80°,
∴∠EGC=80°.
故选:B.
5.D
【分析】由平行四边形的性质进行判断,即可得到答案.
解:由题意可知,
∵,,
∴四边形是平行四边形,
∴;故D符合题意;
随着一张纸条在转动过程中,不一定等于,四边形周长、面积都会改变;故A、B、C不符合题意;
故选:D
6.D
【分析】根据平行四边形的判定及性质定理判断即可;
解:平行四边形对角相等,故A错误;
一组对边平行不能判断四边形是平行四边形,故B错误;
三边相等不能判断四边形是平行四边形,故C错误;
一组对边平行且相等的四边形是平行四边形,故D正确;
故选:D.
7.C
【分析】根据平行四边形的对边平行和两直线平行内错角相等的性质,再通过等量代换即可求解.
解:∵四边形ABCD为平行四边形,
∴ABCD
∴∠DCA=∠CAB,
∵∠DCA+∠ACB,,
∴40 +80 =120 ,
故选:C.
8.C
【分析】根据作图步骤可知,得出了对角线互相平分,从而可以判断.
解:根据图1,得出的中点,图2,得出,
可知使得对角线互相平分,从而得出四边形为平行四边形,
判定四边形ABCD为平行四边形的条件是:对角线互相平分,
故选:C.
9.B
【分析】利用平行四边形ABCD的面积公式即可求解.
解:∵DE⊥AB,BF⊥AC,
∴S平行四边形ABCD=DE×AB=2××AC×BF,
∴4×6=2××8×BF,
∴BF=3,
故选:B.
10.C
【分析】先根据平行四边形的性质,得出,根据平行线的性质,得出,根据折叠得出,根据三角形内角和得出∠A的度数即可.
解:∵四边形ABCD为平行四边形,
∴,
,
根据折叠可知,,
∴,
,
∴,故C正确.
故选:C.
二、填空题
11.
【分析】证明,,由,可得,结合,可得.
解:∵,,
∴,,
∵平行四边形ABCD,
∴,
∴,
∵,
∴;
故答案为:
12.10
【分析】由平行四边形的性质可得即,再结合可得可得,最进一步说明即可解答.
解:∵中,
∴,
∴,
∵,
∴,
∴,
∴,即.
故答案为:10.
13.
【分析】可证,从而可得,再证四边形是平行四边形,可得,即可求解.
解:四边形是平行四边形,
,
,
由折叠得:,
,,
,
,
,
,
,
四边形是平行四边形,
.
故答案:.
14.
【分析】根据平行四边形的性质得到,再利用平行线的性质得到即可解答.
解:过点作,
∴
∵,
∴,
∴,
∴,
∵在平行四边形ABCD中,
∴,
∵,
∴,
∵,
∴,
故答案为:.
15.
【分析】根据平行四边形对边平行可得,利用平行线的性质可得,因此利用直角三角形两个锐角互余求出即可.
解:∵四边形是平行四边形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
故答案为:.
16.
【分析】根据平行四边形的性质以及点的平移即可得出结论.
解:四边形为平行四边形,
,即将点平移到的过程与将点平移到的过程保持一致,
将点平移到的过程是:(向左平移4各单位长度);(上下无平移);
将点平移到的过程按照上述一致过程进行得到,即,
故答案为:.
17.110
【分析】先根据等腰三角形的性质求出∠ABC的度数;再根据平行四边形对边平行和两直线平行同旁内角互补的性质,得出∠2+∠ABE=180 ,代入求解即可.
解:∵是等腰三角形,∠A=120 ,
∴∠ABC=∠C=(180 -∠A)÷2=30 ,
∵四边形是平行四边形,
∴OFDE,
∴∠2+∠ABE=180 ,
即∠2+30 +40 =180 ,
∴∠2=110 .
故答案为:110 .
18..
【分析】设与之间的距离为,由条件可知的面积是的面积的2倍,可求得的面积,,因此可求得的长.
解:∵四边形为平行四边形,
∴,,
,
∴,
∵,,,
∴,
∴,
设与之间的距离为,
∵,
∴,
∴,
解得,
故答案为:.
三、解答题
19.
解:证明:∵四边形是平行四边形,
∴,,,,
∵平分,平分,
∴,
在和中,
∴
∴.
20.
解:证明:∵四边形是平行四边形,
∴,,
∵,
∴,即,
又∵,
∴四边形是平行四边形,
∴.
21.
解:证明:,,
,
又,
,
,
∵,
,
四边形是平行四边形.
22.
(1)解:如图,为所作;
(2)证明:,
,
平分,
,
,
即,
,
,
,
四边形是平行四边形.
23.
解:(1)证明:∵点F为边AB的中点,
∴,
在与中,
,
∴;
(2)证明:∵点D为边AC的中点,
∴,
由(1)得,
∴,,
∴,,
∴四边形BCDE是平行四边形.
24.
解:(1)证明:四边形是平行四边形,
,,
,
,
,
又,
四边形是平行四边形.
(2)解:,,
∴S AEF=S ABE=2
四边形是平行四边形,
∴S CFO=S CEF=S AEF=×2=1
