人教版八年级数学下册 18.2.1 矩形(含解析)
文档属性
| 名称 | 人教版八年级数学下册 18.2.1 矩形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1019.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 15:32:22 | ||
图片预览



文档简介
18.2.1 矩形
一、单选题
1.下列性质中,矩形不一定具有的是( )
A. B. C. D.
2.矩形中,,,则的长为( )
A. B. C. D.
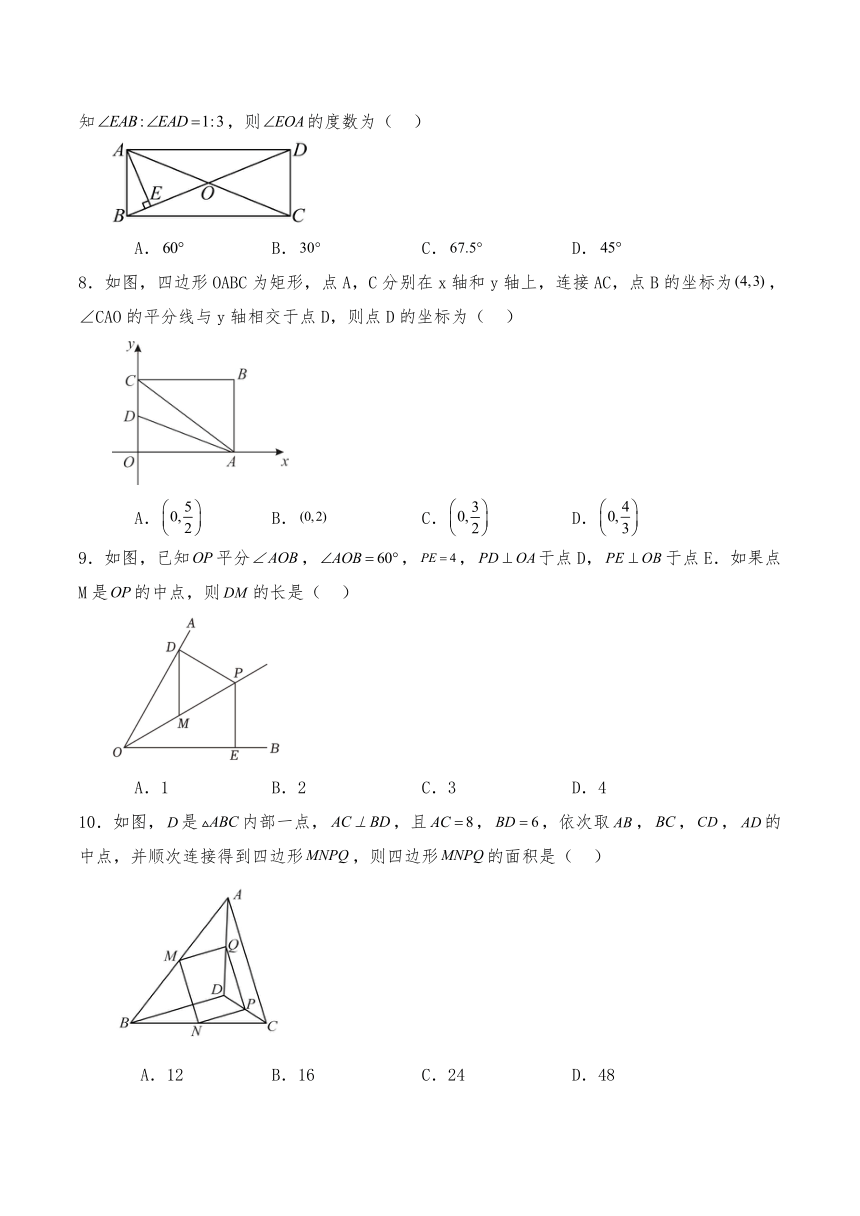
3.如图,在矩形中,,,点E在边上,若平分,则的长为( )
A. B. C. D.
4.下列命题中正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分且相等的四边形是矩形
C.对角线垂直的四边形是矩形 D.对角线相等且垂直的四边形是矩形
5.如图,在四边形中,给出部分数据,若添加一个数据后,四边形是矩形,则添加的数据是( )
A. B. C. D.
6.如图,在长方形中,,,为的中点,点分别在上,若,为等腰直角三角形,则四边形的面积为( )
A.10 B.9 C. D.
7.如图,在矩形中,对角线与相交于点,过点作的垂线,垂足为,已知,则的度数为( )
A. B. C. D.
8.如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为,∠CAO的平分线与y轴相交于点D,则点D的坐标为( )
A. B. C. D.
9.如图,已知平分,,,于点D,于点E.如果点M是的中点,则的长是( )
A.1 B.2 C.3 D.4
10.如图,是内部一点,,且,,依次取,,,的中点,并顺次连接得到四边形,则四边形的面积是( )
A.12 B.16 C.24 D.48
二、填空题
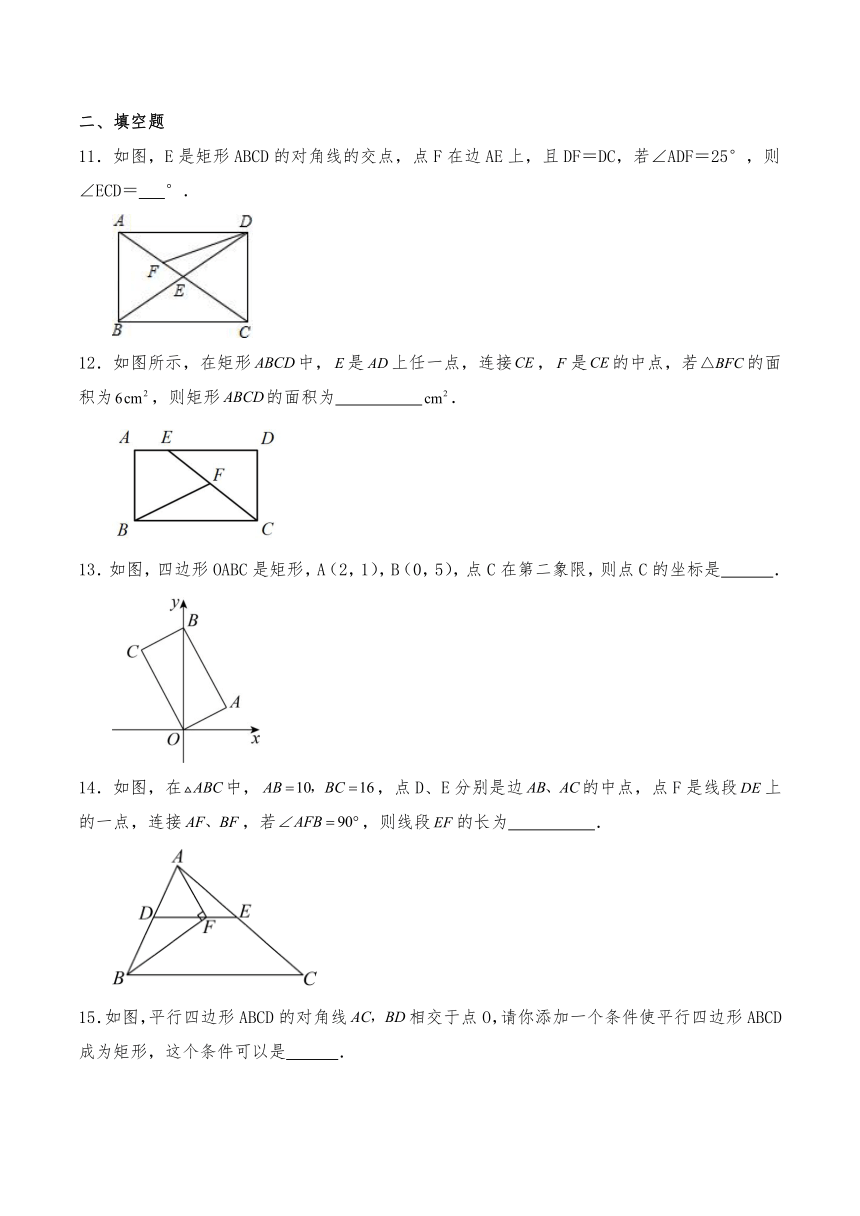
11.如图,E是矩形ABCD的对角线的交点,点F在边AE上,且DF=DC,若∠ADF=25°,则∠ECD= °.
12.如图所示,在矩形中,是上任一点,连接,是的中点,若的面积为,则矩形的面积为 .
13.如图,四边形OABC是矩形,A(2,1),B(0,5),点C在第二象限,则点C的坐标是 .
14.如图,在中,,点D、E分别是边的中点,点F是线段上的一点,连接,若,则线段的长为 .
15.如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件使平行四边形ABCD成为矩形,这个条件可以是 .
16.如图,长方形中,,,长方形内有一个点,连接,,,已知,,延长交于点,则 .
17.如图,在矩形ABCD中,AB=3,BC=4.点E在边AD上,且ED=3,M,N分别是边AB,BC上的动点,且BM=BN,P是线段CE上的动点,连接PM,PN.若PM+PN=4,则线段PC的长为 .
18.如图,矩形纸片的对角线,相交于点,,将矩形纸片翻折,使点恰好落在点处,折痕为,点在边上,则的长为 .
三、解答题
19.如图,已知四边形是平行四边形,对角线交于点是等边三角形.
(1)求证:四边形是矩形;
(2)若,求的长.
20.(8分)如图,在中,D为斜边的中点,E为上一点,F为中点,若,.
(1)求证:为的角平分线;
(2)求的长.
21.如图,在平行四边形ABCD中,点E,F分别在,上,连接,,,,且.请从以下三个选项中:①;②;③,选择一个合适的选项作为已知条件,使四边形是矩形.(不再添加其他线条和字母).
(1)你添加的条件是: ;(填序号,填一个即可)
(2)添加条件后,请证明四边形是矩形.
22.如图,在梯形中,,F为上一点,且,E为上一点,交于点G.
(1)求证:四边形是矩形;
(2)若,求证:.
23.如图,在中,已知,过点C作于点D,过点B作于点M,与相交于点E,且点E是的中点,连接,过点D作,交于点N.
(1)求证:;
(2)请探究线段、、之间的数量关系,并证明你的结论.
24.(12分)综合与探究
如图,在平面直角坐标系中,长方形,,.在上取一点,沿折叠,点恰好落在上的点处.
(1)点的坐标为___________.
(2)求点的坐标;
(3)若点是平面内一点,是否存在点,使得以、、、为顶点的四边形是平行四边形,若存在,直接写出点的坐标,若不存在,请说明理由.
答案:
一、单选题
1.A
【分析】根据矩形的性质,进行判断即可.
解:∵矩形,
∴,,;
矩形的邻边不一定相等,
故选A.
2.C
【分析】此题考查了矩形的性质,根据矩形的对角线相等即可求解,解题的关键是熟练掌握矩形的性质及其应用.
解:∵四边形是矩形,
∴,
故选:.
3.C
【分析】利用角平分线和平行线内错角相等,可证明,则ED=AD,则可用勾股定理求出ED.
解:∵四边形是矩形,
∴,AB=CE=3
∴
∵平分
∴
∴
∴ED=AD=4
∴
故选: C.
4.B
【分析】根据矩形的判定方法逐一分析即可.
解:对角线相等的平行四边形是矩形,故A不符合题意;
对角线互相平分且相等的四边形是矩形,表述正确,故B符合题意;
对角线垂直的四边形不一定是矩形,故C不符合题意;
对角线相等且垂直的四边形不一定是矩形,故D不符合题意;
故选B
5.D
【分析】根据对角线互相平分的四边形是平行四边形,对角线相等的平行四边形是矩形即可得到答案.
解:当时,由题意可知,
,,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
故选:D
6.D
【分析】首先根据等腰三角形的性质证得△AEG≌△DGF,从而得到AE=DG=2,AG=DF=3,从而求得CF的长度,然后利用梯形面积公式求解.
解:∵△GEF为等腰直角三角形,
∴GE=GF,∠EGF=90°,
∴∠AGE+∠DGF=90°,
又∵在长方形中∠AEG+∠AGE=90°,
∴∠AEG=∠DGF,
∴△AEG≌△DGF,
∴AE=GD,AG=DF,
∵AB=4,AD=5,E为AB的中点,点F,G分别在CD,AD上,
∴BE=AE=GD=2,AG=DF=3,
∴CF=1,
∴四边形的面积为
故选:D
7.D
【分析】本题考查矩形的性质,等腰三角形的性质.根据,可以求得的度数,再根据矩形的性质和三角形内角和,即可得到的度数.
解:∵四边形是矩形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
即的度数为,
故选:D.
8.D
【分析】根据题意可知AD平分∠CAO,过D点作DE⊥AC于点E,利用角平分线的性质可知OD=OE,利用等面积法即可求出结果.
解:过D点作DE⊥AC于点E,如图所示,
∵AD平分∠CAO,
∴DO=DE,
∵点B的坐标为,
∴OA=4,OC=3,
∴,
∴,
∴,
∴OD=,
∴D点坐标为(0,),
故选:D.
9.D
【分析】本题主要考查了角平分线的性质,含30度角直角三角形的性质,直角三角形性质,解题的关键是熟练掌握直角三角形斜边中线等于斜边的一半.根据角平分线的性质得出,,根据含30度角直角三角形的性质,得出,最后得出.
解:∵平分,,
∴,
∵,,,
∴,,
∴,
∵点M是的中点,
∴.
故选:D.
10.A
【分析】本题主要考查了三角形中位线定理,矩形的性质与判定,先根据三角形中位线定理可得,,,从而可得,再根据平行四边形的判定可得四边形是平行四边形,然后根据平行线的性质可得,根据矩形的判定可得平行四边形是矩形,最后利用矩形的面积公式求解即可得.
解:点分别是,的中点,且,
,
同理可得:,,
,
四边形是平行四边形,
,
,
又,
,
平行四边形是矩形,
∴四边形的面积是,
故选:A.
二、填空题
11.57.5.
【分析】根据矩形的性质由∠ADF求出∠CDF,再由等腰三角形的性质得出∠ECD即可.
解:∵四边形ABCD是矩形,
∴∠ADC=90°,
∵∠ADF=25°,
∴∠CDF=∠ADC﹣∠ADF=90°﹣25°=65°,
∵DF=DC,
∴∠ECD=,
故答案为:57.5.
12.24
【分析】根据矩形的性质和三角形中线的性质,求解即可.
解:连接,
是的中线,的面积为,
,
又∵矩形与同底等高,
矩形的面积.
故答案为:.
13.(﹣2,4)
【分析】作AM⊥x轴于M,CN⊥y轴于N,则∠AMO=∠BNC=90°,OM=2,AM=1,OB=5,证明△BCN≌△AOM(AAS),得出BN=AM=1,CN=OM=2,得出ON=OB﹣BN=4,即可得出答案.
解:作AM⊥x轴于M,CN⊥y轴于N,如图所示:
则∠AMO=∠BNC=90°,
∴∠AOM+∠OAM=90°,
∵A(2,1),B(0,5),
∴OM=2,AM=1,OB=5,
∵四边形OABC是矩形,
∴BC=AO,∠AOC=90°,BC∥OA,
∴∠CBN=∠AOB,
∵∠AOM+∠AOB=90°,
∴∠CBN=∠AOB=∠OAM,
在△BCN和△AOM中, ,
∴△BCN≌△AOM(AAS),
∴BN=AM=1,CN=OM=2,
∴ON=OB﹣BN=4,
∴点C的坐标是(﹣2,4);
故答案为(﹣2,4).
14.3
【分析】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线性质是解题的关键.先根据直角三角形斜边上的中线等于斜边的一半可以得到的长,然后利用三角形的中位线求出长,再利用解题即可.
解:∵,点D是的中点,
∴,
∵D、E分别是,的中点,
∴,
∴,
故答案为3.
15.(答案不唯一)
【分析】依据矩形的判定定理进行判断即可.
解:∵四边形为平行四边形,
∴当时,四边形为矩形.
故答案为(答案不唯一).
16.
【分析】此题考查矩形的性质、等腰三角形的判定和性质以及勾股定理,延长交于F,根据已知条件得到,根据矩形的性质得到,,根据余角的性质得到,进一步推出,根据勾股定理即可得到结论.
解:延长交于点F,如图,
∵,
∴,
∴,
∵四边形是矩形,
∴,,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,解得.
故答案为:.
17.2
解:∵DE=AB=CD=3,
∴△CDE是等腰直角三角形.
作点N关于EC的对称点N',则点N'在直线CD上,连接PN',如图:
∵PM+PN=4.∴PM+PN'=4=BC,即MN'=4,
此时M,P,N'三点共线且MN'∥BC,∴四边形MBCN'是矩形,
∴BM=CN',∠PN'C=90°.
∵BM=BN,CN=CN',
∴BN=CN=BC=2,
∴PM=PN'=2,∴PC=2.
18.
【分析】本题考查翻折变换,等边三角形的判定和性质,含30度的直角三角形的性质;首先证明是等边三角形,根据含30度角的直角三角形的性质得出,证明,根据,即可求解.
解:四边形是矩形,
,,
由翻折性质可知:,,
,
是等边三角形,
,
,,则
,,
,
故答案为:6.
三、解答题
19.
解:(1)证明:四边形是平行四边形,
.
是等边三角形,
,
,
四边形是矩形.
(2)解:四边形是矩形,
.
是等边三角形,
,则,
.
20.
解:(1)证明:∵,
∴,
∵D为斜边的中点,F为中点,
∴是的中位线,
∴,
∴,
∴,
∴为的角平分线;
(2)解:∵D为斜边的中点,F为中点,,
∴,
∵,
∴,
在中,D为斜边的中点,
∴.
21.
解:(1)解:根据平行四边形性质与判定,矩形的判定,选择①(或②),选择其中一个序号填写即可.
(2)解:证明:若选①判定如下:
∵四边形是平行四边形,
∴,,,
∵,
∴在和中,
,
∴,
∴,
∵,
∴为平行四边形,
∵,
∴为矩形;
若选②判定如下:
解:∵四边形是平行四边形,
∴,
∵,
∴为平行四边形,
∵,
∴为矩形.
22.
解:(1)证明:∵,
∴四边形是平行四边形.
∵,
∴四边形是矩形.
(2)证明:∵四边形是矩形,
∴,
∴.
∵,
∴.
∴.
∵,
∴.
∴.
23.
解:(1)证明:∵,,
∴,
∴,
∵,
∴,
∵,,
∴,
在和中,
∴.
(2)结论:.
由(1)可得.
作于点F,
又,
∴,
∵点是的中点,
∴,
在和中,
,
∴,
∴,,
∴.
24.
(1)解:∵
∴点的坐标为
故答案为:
(2)解:由题意得:
∴
设,则
在中:
解得:
∴点
(3)解:由题意得可得:
设点
为对角线,则有:
解得:
故
为对角线,则有:
解得:
故
为对角线,则有:
解得:
故
综上所述:
一、单选题
1.下列性质中,矩形不一定具有的是( )
A. B. C. D.
2.矩形中,,,则的长为( )
A. B. C. D.
3.如图,在矩形中,,,点E在边上,若平分,则的长为( )
A. B. C. D.
4.下列命题中正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分且相等的四边形是矩形
C.对角线垂直的四边形是矩形 D.对角线相等且垂直的四边形是矩形
5.如图,在四边形中,给出部分数据,若添加一个数据后,四边形是矩形,则添加的数据是( )
A. B. C. D.
6.如图,在长方形中,,,为的中点,点分别在上,若,为等腰直角三角形,则四边形的面积为( )
A.10 B.9 C. D.
7.如图,在矩形中,对角线与相交于点,过点作的垂线,垂足为,已知,则的度数为( )
A. B. C. D.
8.如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为,∠CAO的平分线与y轴相交于点D,则点D的坐标为( )
A. B. C. D.
9.如图,已知平分,,,于点D,于点E.如果点M是的中点,则的长是( )
A.1 B.2 C.3 D.4
10.如图,是内部一点,,且,,依次取,,,的中点,并顺次连接得到四边形,则四边形的面积是( )
A.12 B.16 C.24 D.48
二、填空题
11.如图,E是矩形ABCD的对角线的交点,点F在边AE上,且DF=DC,若∠ADF=25°,则∠ECD= °.
12.如图所示,在矩形中,是上任一点,连接,是的中点,若的面积为,则矩形的面积为 .
13.如图,四边形OABC是矩形,A(2,1),B(0,5),点C在第二象限,则点C的坐标是 .
14.如图,在中,,点D、E分别是边的中点,点F是线段上的一点,连接,若,则线段的长为 .
15.如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件使平行四边形ABCD成为矩形,这个条件可以是 .
16.如图,长方形中,,,长方形内有一个点,连接,,,已知,,延长交于点,则 .
17.如图,在矩形ABCD中,AB=3,BC=4.点E在边AD上,且ED=3,M,N分别是边AB,BC上的动点,且BM=BN,P是线段CE上的动点,连接PM,PN.若PM+PN=4,则线段PC的长为 .
18.如图,矩形纸片的对角线,相交于点,,将矩形纸片翻折,使点恰好落在点处,折痕为,点在边上,则的长为 .
三、解答题
19.如图,已知四边形是平行四边形,对角线交于点是等边三角形.
(1)求证:四边形是矩形;
(2)若,求的长.
20.(8分)如图,在中,D为斜边的中点,E为上一点,F为中点,若,.
(1)求证:为的角平分线;
(2)求的长.
21.如图,在平行四边形ABCD中,点E,F分别在,上,连接,,,,且.请从以下三个选项中:①;②;③,选择一个合适的选项作为已知条件,使四边形是矩形.(不再添加其他线条和字母).
(1)你添加的条件是: ;(填序号,填一个即可)
(2)添加条件后,请证明四边形是矩形.
22.如图,在梯形中,,F为上一点,且,E为上一点,交于点G.
(1)求证:四边形是矩形;
(2)若,求证:.
23.如图,在中,已知,过点C作于点D,过点B作于点M,与相交于点E,且点E是的中点,连接,过点D作,交于点N.
(1)求证:;
(2)请探究线段、、之间的数量关系,并证明你的结论.
24.(12分)综合与探究
如图,在平面直角坐标系中,长方形,,.在上取一点,沿折叠,点恰好落在上的点处.
(1)点的坐标为___________.
(2)求点的坐标;
(3)若点是平面内一点,是否存在点,使得以、、、为顶点的四边形是平行四边形,若存在,直接写出点的坐标,若不存在,请说明理由.
答案:
一、单选题
1.A
【分析】根据矩形的性质,进行判断即可.
解:∵矩形,
∴,,;
矩形的邻边不一定相等,
故选A.
2.C
【分析】此题考查了矩形的性质,根据矩形的对角线相等即可求解,解题的关键是熟练掌握矩形的性质及其应用.
解:∵四边形是矩形,
∴,
故选:.
3.C
【分析】利用角平分线和平行线内错角相等,可证明,则ED=AD,则可用勾股定理求出ED.
解:∵四边形是矩形,
∴,AB=CE=3
∴
∵平分
∴
∴
∴ED=AD=4
∴
故选: C.
4.B
【分析】根据矩形的判定方法逐一分析即可.
解:对角线相等的平行四边形是矩形,故A不符合题意;
对角线互相平分且相等的四边形是矩形,表述正确,故B符合题意;
对角线垂直的四边形不一定是矩形,故C不符合题意;
对角线相等且垂直的四边形不一定是矩形,故D不符合题意;
故选B
5.D
【分析】根据对角线互相平分的四边形是平行四边形,对角线相等的平行四边形是矩形即可得到答案.
解:当时,由题意可知,
,,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
故选:D
6.D
【分析】首先根据等腰三角形的性质证得△AEG≌△DGF,从而得到AE=DG=2,AG=DF=3,从而求得CF的长度,然后利用梯形面积公式求解.
解:∵△GEF为等腰直角三角形,
∴GE=GF,∠EGF=90°,
∴∠AGE+∠DGF=90°,
又∵在长方形中∠AEG+∠AGE=90°,
∴∠AEG=∠DGF,
∴△AEG≌△DGF,
∴AE=GD,AG=DF,
∵AB=4,AD=5,E为AB的中点,点F,G分别在CD,AD上,
∴BE=AE=GD=2,AG=DF=3,
∴CF=1,
∴四边形的面积为
故选:D
7.D
【分析】本题考查矩形的性质,等腰三角形的性质.根据,可以求得的度数,再根据矩形的性质和三角形内角和,即可得到的度数.
解:∵四边形是矩形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
即的度数为,
故选:D.
8.D
【分析】根据题意可知AD平分∠CAO,过D点作DE⊥AC于点E,利用角平分线的性质可知OD=OE,利用等面积法即可求出结果.
解:过D点作DE⊥AC于点E,如图所示,
∵AD平分∠CAO,
∴DO=DE,
∵点B的坐标为,
∴OA=4,OC=3,
∴,
∴,
∴,
∴OD=,
∴D点坐标为(0,),
故选:D.
9.D
【分析】本题主要考查了角平分线的性质,含30度角直角三角形的性质,直角三角形性质,解题的关键是熟练掌握直角三角形斜边中线等于斜边的一半.根据角平分线的性质得出,,根据含30度角直角三角形的性质,得出,最后得出.
解:∵平分,,
∴,
∵,,,
∴,,
∴,
∵点M是的中点,
∴.
故选:D.
10.A
【分析】本题主要考查了三角形中位线定理,矩形的性质与判定,先根据三角形中位线定理可得,,,从而可得,再根据平行四边形的判定可得四边形是平行四边形,然后根据平行线的性质可得,根据矩形的判定可得平行四边形是矩形,最后利用矩形的面积公式求解即可得.
解:点分别是,的中点,且,
,
同理可得:,,
,
四边形是平行四边形,
,
,
又,
,
平行四边形是矩形,
∴四边形的面积是,
故选:A.
二、填空题
11.57.5.
【分析】根据矩形的性质由∠ADF求出∠CDF,再由等腰三角形的性质得出∠ECD即可.
解:∵四边形ABCD是矩形,
∴∠ADC=90°,
∵∠ADF=25°,
∴∠CDF=∠ADC﹣∠ADF=90°﹣25°=65°,
∵DF=DC,
∴∠ECD=,
故答案为:57.5.
12.24
【分析】根据矩形的性质和三角形中线的性质,求解即可.
解:连接,
是的中线,的面积为,
,
又∵矩形与同底等高,
矩形的面积.
故答案为:.
13.(﹣2,4)
【分析】作AM⊥x轴于M,CN⊥y轴于N,则∠AMO=∠BNC=90°,OM=2,AM=1,OB=5,证明△BCN≌△AOM(AAS),得出BN=AM=1,CN=OM=2,得出ON=OB﹣BN=4,即可得出答案.
解:作AM⊥x轴于M,CN⊥y轴于N,如图所示:
则∠AMO=∠BNC=90°,
∴∠AOM+∠OAM=90°,
∵A(2,1),B(0,5),
∴OM=2,AM=1,OB=5,
∵四边形OABC是矩形,
∴BC=AO,∠AOC=90°,BC∥OA,
∴∠CBN=∠AOB,
∵∠AOM+∠AOB=90°,
∴∠CBN=∠AOB=∠OAM,
在△BCN和△AOM中, ,
∴△BCN≌△AOM(AAS),
∴BN=AM=1,CN=OM=2,
∴ON=OB﹣BN=4,
∴点C的坐标是(﹣2,4);
故答案为(﹣2,4).
14.3
【分析】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线性质是解题的关键.先根据直角三角形斜边上的中线等于斜边的一半可以得到的长,然后利用三角形的中位线求出长,再利用解题即可.
解:∵,点D是的中点,
∴,
∵D、E分别是,的中点,
∴,
∴,
故答案为3.
15.(答案不唯一)
【分析】依据矩形的判定定理进行判断即可.
解:∵四边形为平行四边形,
∴当时,四边形为矩形.
故答案为(答案不唯一).
16.
【分析】此题考查矩形的性质、等腰三角形的判定和性质以及勾股定理,延长交于F,根据已知条件得到,根据矩形的性质得到,,根据余角的性质得到,进一步推出,根据勾股定理即可得到结论.
解:延长交于点F,如图,
∵,
∴,
∴,
∵四边形是矩形,
∴,,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,解得.
故答案为:.
17.2
解:∵DE=AB=CD=3,
∴△CDE是等腰直角三角形.
作点N关于EC的对称点N',则点N'在直线CD上,连接PN',如图:
∵PM+PN=4.∴PM+PN'=4=BC,即MN'=4,
此时M,P,N'三点共线且MN'∥BC,∴四边形MBCN'是矩形,
∴BM=CN',∠PN'C=90°.
∵BM=BN,CN=CN',
∴BN=CN=BC=2,
∴PM=PN'=2,∴PC=2.
18.
【分析】本题考查翻折变换,等边三角形的判定和性质,含30度的直角三角形的性质;首先证明是等边三角形,根据含30度角的直角三角形的性质得出,证明,根据,即可求解.
解:四边形是矩形,
,,
由翻折性质可知:,,
,
是等边三角形,
,
,,则
,,
,
故答案为:6.
三、解答题
19.
解:(1)证明:四边形是平行四边形,
.
是等边三角形,
,
,
四边形是矩形.
(2)解:四边形是矩形,
.
是等边三角形,
,则,
.
20.
解:(1)证明:∵,
∴,
∵D为斜边的中点,F为中点,
∴是的中位线,
∴,
∴,
∴,
∴为的角平分线;
(2)解:∵D为斜边的中点,F为中点,,
∴,
∵,
∴,
在中,D为斜边的中点,
∴.
21.
解:(1)解:根据平行四边形性质与判定,矩形的判定,选择①(或②),选择其中一个序号填写即可.
(2)解:证明:若选①判定如下:
∵四边形是平行四边形,
∴,,,
∵,
∴在和中,
,
∴,
∴,
∵,
∴为平行四边形,
∵,
∴为矩形;
若选②判定如下:
解:∵四边形是平行四边形,
∴,
∵,
∴为平行四边形,
∵,
∴为矩形.
22.
解:(1)证明:∵,
∴四边形是平行四边形.
∵,
∴四边形是矩形.
(2)证明:∵四边形是矩形,
∴,
∴.
∵,
∴.
∴.
∵,
∴.
∴.
23.
解:(1)证明:∵,,
∴,
∴,
∵,
∴,
∵,,
∴,
在和中,
∴.
(2)结论:.
由(1)可得.
作于点F,
又,
∴,
∵点是的中点,
∴,
在和中,
,
∴,
∴,,
∴.
24.
(1)解:∵
∴点的坐标为
故答案为:
(2)解:由题意得:
∴
设,则
在中:
解得:
∴点
(3)解:由题意得可得:
设点
为对角线,则有:
解得:
故
为对角线,则有:
解得:
故
为对角线,则有:
解得:
故
综上所述:
