数学:4.4《对数的概念及运算》课件(2)(沪教版高一下)
文档属性
| 名称 | 数学:4.4《对数的概念及运算》课件(2)(沪教版高一下) |

|
|
| 格式 | rar | ||
| 文件大小 | 365.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-18 13:48:00 | ||
图片预览






文档简介
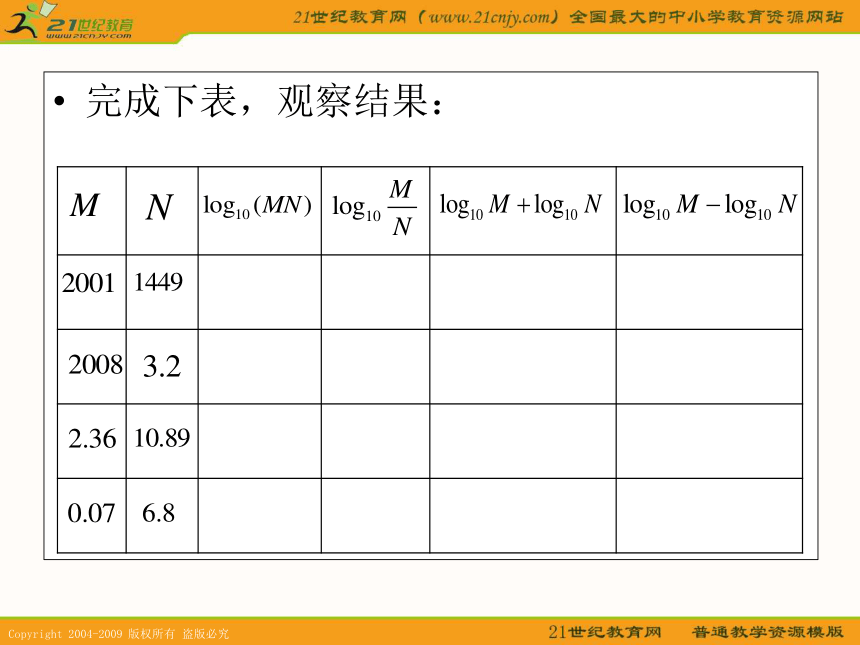
课件15张PPT。对数的运算 完成下表,观察结果: 猜测:
等式中各字母的范围:
在猜测的基础上能否在给出一些特例?提示:当M=N时,得到推广: 推广中,k的范围能否再拓展一些? 积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:为了证明以上公式,请同学们回顾一下指数运算法则 :证明:①设 由对数的定义可以得: ∴MN= 即证得 证明:②设 由对数的定义可以得: ∴ 即证得 证明:③设 由对数的定义可以得: ∴即证得 例1:判断下列各式是否成立,如果成立,请给出证明;若不成立,请给出反例。 例2:计算:例3:已知 ,求 科学家以里氏震级来度量地震的强度,若设I为地震时所散发出来的相对能量程度,则里氏震级量度r可定义为 ,试比较6.9级和7.8级地震的相对能量的比值。(精确到个位) 拓展(1) 练习计算: (2) (3) 小结 :积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:课后作业: 书后练习1、2、3、4做在书上,5做在练习本上;练习册第1页第4、5题做在练习本上。
等式中各字母的范围:
在猜测的基础上能否在给出一些特例?提示:当M=N时,得到推广: 推广中,k的范围能否再拓展一些? 积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:为了证明以上公式,请同学们回顾一下指数运算法则 :证明:①设 由对数的定义可以得: ∴MN= 即证得 证明:②设 由对数的定义可以得: ∴ 即证得 证明:③设 由对数的定义可以得: ∴即证得 例1:判断下列各式是否成立,如果成立,请给出证明;若不成立,请给出反例。 例2:计算:例3:已知 ,求 科学家以里氏震级来度量地震的强度,若设I为地震时所散发出来的相对能量程度,则里氏震级量度r可定义为 ,试比较6.9级和7.8级地震的相对能量的比值。(精确到个位) 拓展(1) 练习计算: (2) (3) 小结 :积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:课后作业: 书后练习1、2、3、4做在书上,5做在练习本上;练习册第1页第4、5题做在练习本上。
