2025年九年级中考数学三轮冲刺训练分式专题训练(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练分式专题训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 48.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 15:30:56 | ||
图片预览


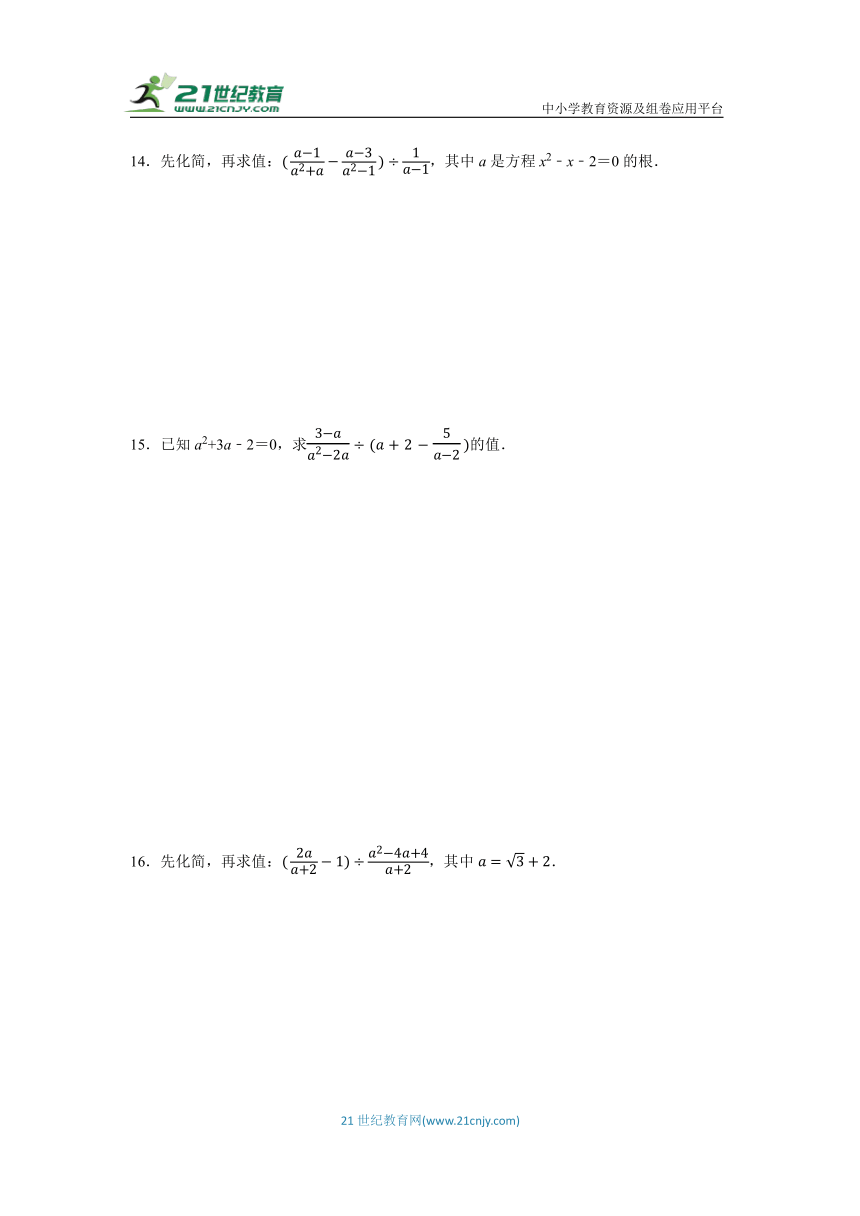

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练分式专题训练
一、选择题
1.如果把分式中的x和y都扩大2倍,那么分式的值( )
A.缩小到原来的 B.扩大2倍
C.不变 D.缩小到原来的
2.已知:m2﹣m﹣2025=0,则的值为( )
A. B. C.2025 D.﹣2025
3.已知一列均不为1的数a1,a2,a3,…,an满足如下关系:a2,a3,a4,…,an+1,若a1=2,则a2025的值是( )
A. B. C.﹣3 D.2
4.若x2+3x=﹣1,则式子x的值是( )
A.﹣2 B.0 C.1 D.2
5.已知,则的值为( )
A. B. C. D.
6.设x为实数,已知实数x满足x2=3x+1.则的值为( )
A.0 B.1 C.2 D.3
二、填空题
7.若m2,则m2 .
8.设a>1,a2+1=6a,则的值为 .
9.若4a2+b2﹣5ab=0,则的值等于 .
10.若x满足(x+1)2x﹣1=1,则x的值为 .
11.若am=10,bn=10,ab=10,则 .
三、解答题
12.已知x﹣y﹣5=0,求代数式的值.
13.先化简,再求值:,请从0,1、2、3中选取一个合适的数作为x的值.
14.先化简,再求值:,其中a是方程x2﹣x﹣2=0的根.
15.已知a2+3a﹣2=0,求的值.
16.先化简,再求值:,其中.
参考答案
一、选择题
1.【解答】解:根据题意可知,,
∴分式的值缩小到原来的.
故选:A.
2.【解答】解:原式
=﹣m(m﹣1)
=﹣m2+m,
∵m2﹣m﹣2025=0,
∴m2﹣m=2025,
∴原式=﹣(m2﹣m)=﹣2025.
故选:D.
3.【解答】解:由题意可得,
当a1=2时,a2=﹣3,a3,a4,a5=2,…,
由上可得,每四个为一个循环,依次以2,﹣3,,出现,
∵2025÷4=506……1,
∴a2025=a1=2,
故选:D.
4.【解答】解:当x2+3x=﹣1时,
∴x2﹣1=﹣3x﹣2,
原式
=﹣2,
故选:A.
5.【解答】解:∵,
∴(x)2=9,
∴x2+29,
∴x27,
∴x2+18,
∴.
故选:B.
6.【解答】解:∵x2=3x+1,
∴x2﹣1=3x,,
∴,
∴,
∴,
∴
=3×11﹣32
=1,
故选:B.
二、填空题
7.【解答】解:∵m2,
∴m22=4,
则m26,
故答案为:6.
8.【解答】解:由条件可知a2﹣6a+1=0,a2=6a﹣1,
∴或(不合题意,舍去),
∴原式
.
故答案为:.
9.【解答】解:∵4a2+b2﹣5ab=0,
∴(4a﹣b)(a﹣b)=0,
∴4a﹣b=0或a﹣b=0,
4a=b或a=b,
当4a=b时,;
当a=b时,;
∴的值等于3或﹣3,
故答案为:3或﹣3.
10.【解答】解:当底数为1时,
当x+1=1时,即x=0,
把x=0代入指数2x﹣1,得0﹣1=﹣1,
则(x+1)2x﹣1=1﹣1=1,满足条件;
当底数为﹣1时,
当x+1=﹣1时,即x=﹣2,
把x=﹣2代入指数2x﹣1,得2×(﹣2)﹣1=﹣5,
则(x+1)2x﹣1=(﹣1)﹣5=﹣1,不满足条件;
当指数为0时,
当2x﹣1=0时,即,
把代入底数x+1,得,
则,满足条件,
综上,x的值为0或.
故答案为:0或.
11.【解答】解:∵am=10,bn=10,ab=10,
∴(ab)m=ambm=10m,(ab)n=anbn=10n,
∴(ab)m (ab)n=(ab)m+n=10m×10n=10m+n,(ab)mn=(am)n (bn)m=10n×10m=10m+n,
∴(ab)m+n=(ab)mn,
∴m+n=mn,
∴,
故答案为:1.
三、解答题
12.【解答】解:
=2(x﹣y)
=2x﹣2y,
∵x﹣y﹣5=0.
∴x﹣y=5,
∴当x﹣y=5时,原式=2(x﹣y)=2×5=10.
13.【解答】解:
,
∵x﹣1≠0,x﹣3≠0,x≠0,
∴x≠1,x≠3,x≠0,
∴当x=2时,原式.
14.【解答】解:
,
解方程x2﹣x﹣2=0,得x1=2,x2=﹣1,
∵a≠±1,
∴x2=﹣1不合题意,舍去,
∴把a=x1=2代入得,
原式.
15.【解答】解:原式
,
∵a2+3a﹣2=0,
∴a2+3a=2,
∴原式.
16.【解答】解:原式
,
当a2时,原式.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练分式专题训练
一、选择题
1.如果把分式中的x和y都扩大2倍,那么分式的值( )
A.缩小到原来的 B.扩大2倍
C.不变 D.缩小到原来的
2.已知:m2﹣m﹣2025=0,则的值为( )
A. B. C.2025 D.﹣2025
3.已知一列均不为1的数a1,a2,a3,…,an满足如下关系:a2,a3,a4,…,an+1,若a1=2,则a2025的值是( )
A. B. C.﹣3 D.2
4.若x2+3x=﹣1,则式子x的值是( )
A.﹣2 B.0 C.1 D.2
5.已知,则的值为( )
A. B. C. D.
6.设x为实数,已知实数x满足x2=3x+1.则的值为( )
A.0 B.1 C.2 D.3
二、填空题
7.若m2,则m2 .
8.设a>1,a2+1=6a,则的值为 .
9.若4a2+b2﹣5ab=0,则的值等于 .
10.若x满足(x+1)2x﹣1=1,则x的值为 .
11.若am=10,bn=10,ab=10,则 .
三、解答题
12.已知x﹣y﹣5=0,求代数式的值.
13.先化简,再求值:,请从0,1、2、3中选取一个合适的数作为x的值.
14.先化简,再求值:,其中a是方程x2﹣x﹣2=0的根.
15.已知a2+3a﹣2=0,求的值.
16.先化简,再求值:,其中.
参考答案
一、选择题
1.【解答】解:根据题意可知,,
∴分式的值缩小到原来的.
故选:A.
2.【解答】解:原式
=﹣m(m﹣1)
=﹣m2+m,
∵m2﹣m﹣2025=0,
∴m2﹣m=2025,
∴原式=﹣(m2﹣m)=﹣2025.
故选:D.
3.【解答】解:由题意可得,
当a1=2时,a2=﹣3,a3,a4,a5=2,…,
由上可得,每四个为一个循环,依次以2,﹣3,,出现,
∵2025÷4=506……1,
∴a2025=a1=2,
故选:D.
4.【解答】解:当x2+3x=﹣1时,
∴x2﹣1=﹣3x﹣2,
原式
=﹣2,
故选:A.
5.【解答】解:∵,
∴(x)2=9,
∴x2+29,
∴x27,
∴x2+18,
∴.
故选:B.
6.【解答】解:∵x2=3x+1,
∴x2﹣1=3x,,
∴,
∴,
∴,
∴
=3×11﹣32
=1,
故选:B.
二、填空题
7.【解答】解:∵m2,
∴m22=4,
则m26,
故答案为:6.
8.【解答】解:由条件可知a2﹣6a+1=0,a2=6a﹣1,
∴或(不合题意,舍去),
∴原式
.
故答案为:.
9.【解答】解:∵4a2+b2﹣5ab=0,
∴(4a﹣b)(a﹣b)=0,
∴4a﹣b=0或a﹣b=0,
4a=b或a=b,
当4a=b时,;
当a=b时,;
∴的值等于3或﹣3,
故答案为:3或﹣3.
10.【解答】解:当底数为1时,
当x+1=1时,即x=0,
把x=0代入指数2x﹣1,得0﹣1=﹣1,
则(x+1)2x﹣1=1﹣1=1,满足条件;
当底数为﹣1时,
当x+1=﹣1时,即x=﹣2,
把x=﹣2代入指数2x﹣1,得2×(﹣2)﹣1=﹣5,
则(x+1)2x﹣1=(﹣1)﹣5=﹣1,不满足条件;
当指数为0时,
当2x﹣1=0时,即,
把代入底数x+1,得,
则,满足条件,
综上,x的值为0或.
故答案为:0或.
11.【解答】解:∵am=10,bn=10,ab=10,
∴(ab)m=ambm=10m,(ab)n=anbn=10n,
∴(ab)m (ab)n=(ab)m+n=10m×10n=10m+n,(ab)mn=(am)n (bn)m=10n×10m=10m+n,
∴(ab)m+n=(ab)mn,
∴m+n=mn,
∴,
故答案为:1.
三、解答题
12.【解答】解:
=2(x﹣y)
=2x﹣2y,
∵x﹣y﹣5=0.
∴x﹣y=5,
∴当x﹣y=5时,原式=2(x﹣y)=2×5=10.
13.【解答】解:
,
∵x﹣1≠0,x﹣3≠0,x≠0,
∴x≠1,x≠3,x≠0,
∴当x=2时,原式.
14.【解答】解:
,
解方程x2﹣x﹣2=0,得x1=2,x2=﹣1,
∵a≠±1,
∴x2=﹣1不合题意,舍去,
∴把a=x1=2代入得,
原式.
15.【解答】解:原式
,
∵a2+3a﹣2=0,
∴a2+3a=2,
∴原式.
16.【解答】解:原式
,
当a2时,原式.
21世纪教育网(www.21cnjy.com)
同课章节目录
