北京育才学校2024-2025学年度高一第二学期3月月考数学试卷(PDF版,含答案)
文档属性
| 名称 | 北京育才学校2024-2025学年度高一第二学期3月月考数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 09:51:53 | ||
图片预览

文档简介
北京育才学校2024-2025学年度第二学期
高一数学3月月考试卷
(100分钟)
一、选择题:(本大题共8小题,每小题4分,共32分.)
1.化简sin600°的值是()
8.2
C.
5
2
2.若sinx-cosx<0,则角x的终边位于()
A,第一、二象限
B,第二、三象限
C.第二、四象限
D.第三、四象限
3.下列函数中,最小正周期为π,且图象关于直线x=对称的是(
A.y=sin(2x-
B.y=sin(2x-)
61
c.y=sm(2x+爱
4.函数y=tan是()
A.周期为2π的奇函数
B.周期为二的奇函数
C.周期为π的偶函数
D.周期为2π的偶函数
5.在平面直角坐标系xOy中,角a与角B均以Ox为始边,它们的终边关于y轴对称.产
cosa=25
,则cosB=()
5
4.35
B.、5
c.-25
D.5
5
5
5
6.要得到函数y=sin(4x-)的图象,只需要将函数y=sin4x的图象()
A,向左平移汇个单位
B.向左平移汇个单位
12
3
C.向右平移严个单位
D.向右平移誓个单位
12
3
7.若函数y=si(-马)在[0,ml上单调递增,则m的最大值为(
C.1
D.2
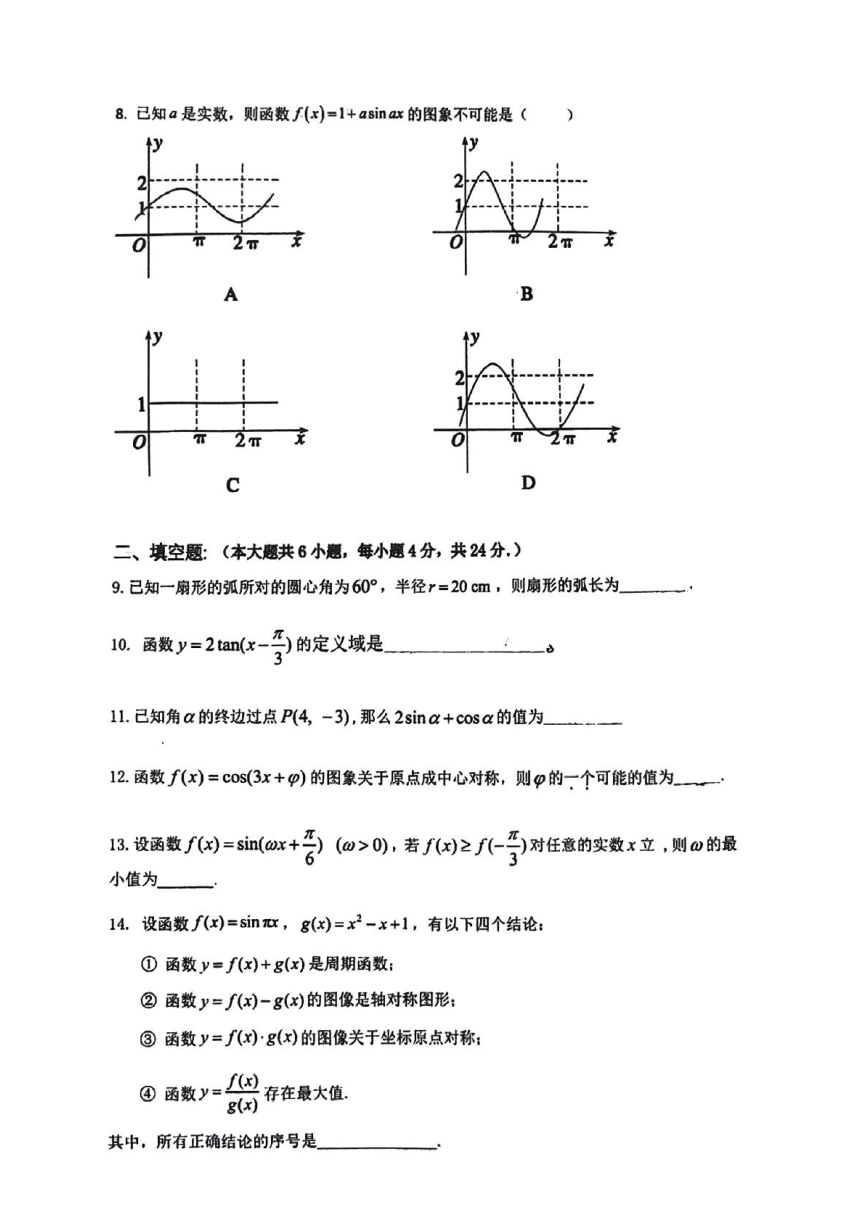
8.已知a是实数,则函数f(x)=1+asin ax的图象不可能是(
二、填空题:(本大题共6小题,每小题4分,共24分,)
9.己知一扇形的弧所对的圆心角为60°,半径r=20cm,则扇形的弧长为
10.
函数y=2tan(x-)的定义域是
3
11.已知角a的终边过点P(4,-3),那么2sina+cosa的值为
12.函数f(x)=Cos(3x+p)的图象关于原点成中心对称,则p的一个可能的值为-
18.设函数四=(ox+ (@>0),若f化2八-孕对任意的实数x立,则 的最
小值为
14.设函数f(x)=sinr,g(x)=x2-x+1,有以下四个结论:
①函数y=f(x)+g(x)是周期函数:
②函数y=f(x)-g(x)的图像是轴对称图形:
③函数y=(x)·g(x)的图像关于坐标原点对称:
@函数y=田
存在最大值
g(x)
其中,所有正确结论的序号是
三、解答题(本大题共4小题,共44分。写出必要的步骤和文字说明。)
1。(本小圆满分7分)已知咖&=5
求cosa,tana,cos(仁+a)的值.
16.(本题13分)已知函数f(x)=Asin(+p)(A>0,ω>0,回<)的部分图象如图
所示。
(1)求出A,0,0的值:
(2),求函数f(x)的单调递增区间和对称轴:
(3)求f()在[0,受1上的最小值,并求出取最小值时x的取值。
本小题满分14分)已知函数f)=Asi(@x+p(4>0,0>0,l<孕,且f)图象的
相邻两条对称轴之间的距离为,再从条件①、条件②、条件③中选择两个作为一组己知条
件.
(T)求函数f(x)的最小正周期:
(IⅡ)求函数f(x)的解析式:
(I)若(x)图象的对称轴只有一条落在区间[0,a]上(a>0),求a的取值范围.
条件①:f(x)的最小值为-2:
条件@:图象的个对称中心为(受0):
条件@:f)的图象经过点(受-).
注:如果选择多组条件分别解答,按第一个解答计分,
,8.,(本小题满分10分)设函数f(x)的定义域为R,若存在常数T,A(T>0,A>0),使得
对于任意x∈R,f(x+T)=f(x)成立,则称函数f(x)具有性质P.
(I)判断函数y=x和y=cosx是否具有性质P?(结论不要求证明)
(Ⅱ)若函数f(x)具有性质P,且其对应的T=元,A=2.己知当x∈(0,时,f(x)=si如x,
求函数f(x)在区间[-元,]上的最大值:
高一数学3月月考试卷
(100分钟)
一、选择题:(本大题共8小题,每小题4分,共32分.)
1.化简sin600°的值是()
8.2
C.
5
2
2.若sinx-cosx<0,则角x的终边位于()
A,第一、二象限
B,第二、三象限
C.第二、四象限
D.第三、四象限
3.下列函数中,最小正周期为π,且图象关于直线x=对称的是(
A.y=sin(2x-
B.y=sin(2x-)
61
c.y=sm(2x+爱
4.函数y=tan是()
A.周期为2π的奇函数
B.周期为二的奇函数
C.周期为π的偶函数
D.周期为2π的偶函数
5.在平面直角坐标系xOy中,角a与角B均以Ox为始边,它们的终边关于y轴对称.产
cosa=25
,则cosB=()
5
4.35
B.、5
c.-25
D.5
5
5
5
6.要得到函数y=sin(4x-)的图象,只需要将函数y=sin4x的图象()
A,向左平移汇个单位
B.向左平移汇个单位
12
3
C.向右平移严个单位
D.向右平移誓个单位
12
3
7.若函数y=si(-马)在[0,ml上单调递增,则m的最大值为(
C.1
D.2
8.已知a是实数,则函数f(x)=1+asin ax的图象不可能是(
二、填空题:(本大题共6小题,每小题4分,共24分,)
9.己知一扇形的弧所对的圆心角为60°,半径r=20cm,则扇形的弧长为
10.
函数y=2tan(x-)的定义域是
3
11.已知角a的终边过点P(4,-3),那么2sina+cosa的值为
12.函数f(x)=Cos(3x+p)的图象关于原点成中心对称,则p的一个可能的值为-
18.设函数四=(ox+ (@>0),若f化2八-孕对任意的实数x立,则 的最
小值为
14.设函数f(x)=sinr,g(x)=x2-x+1,有以下四个结论:
①函数y=f(x)+g(x)是周期函数:
②函数y=f(x)-g(x)的图像是轴对称图形:
③函数y=(x)·g(x)的图像关于坐标原点对称:
@函数y=田
存在最大值
g(x)
其中,所有正确结论的序号是
三、解答题(本大题共4小题,共44分。写出必要的步骤和文字说明。)
1。(本小圆满分7分)已知咖&=5
求cosa,tana,cos(仁+a)的值.
16.(本题13分)已知函数f(x)=Asin(+p)(A>0,ω>0,回<)的部分图象如图
所示。
(1)求出A,0,0的值:
(2),求函数f(x)的单调递增区间和对称轴:
(3)求f()在[0,受1上的最小值,并求出取最小值时x的取值。
本小题满分14分)已知函数f)=Asi(@x+p(4>0,0>0,l<孕,且f)图象的
相邻两条对称轴之间的距离为,再从条件①、条件②、条件③中选择两个作为一组己知条
件.
(T)求函数f(x)的最小正周期:
(IⅡ)求函数f(x)的解析式:
(I)若(x)图象的对称轴只有一条落在区间[0,a]上(a>0),求a的取值范围.
条件①:f(x)的最小值为-2:
条件@:图象的个对称中心为(受0):
条件@:f)的图象经过点(受-).
注:如果选择多组条件分别解答,按第一个解答计分,
,8.,(本小题满分10分)设函数f(x)的定义域为R,若存在常数T,A(T>0,A>0),使得
对于任意x∈R,f(x+T)=f(x)成立,则称函数f(x)具有性质P.
(I)判断函数y=x和y=cosx是否具有性质P?(结论不要求证明)
(Ⅱ)若函数f(x)具有性质P,且其对应的T=元,A=2.己知当x∈(0,时,f(x)=si如x,
求函数f(x)在区间[-元,]上的最大值:
同课章节目录
