2025中考数学二轮复习-二次函数与三角形面积(共22张PPT)
文档属性
| 名称 | 2025中考数学二轮复习-二次函数与三角形面积(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
二次函数与三角形面积
近几年成都中考二次函数与三角形面积考点
近几年成都中考二次函数与三角形面积考点
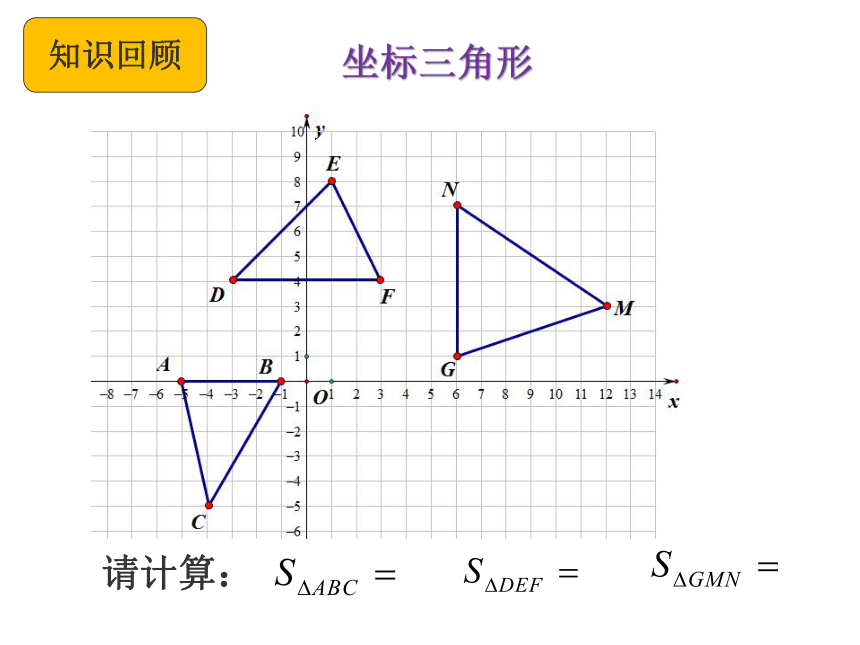
坐标三角形
知识回顾
请计算:
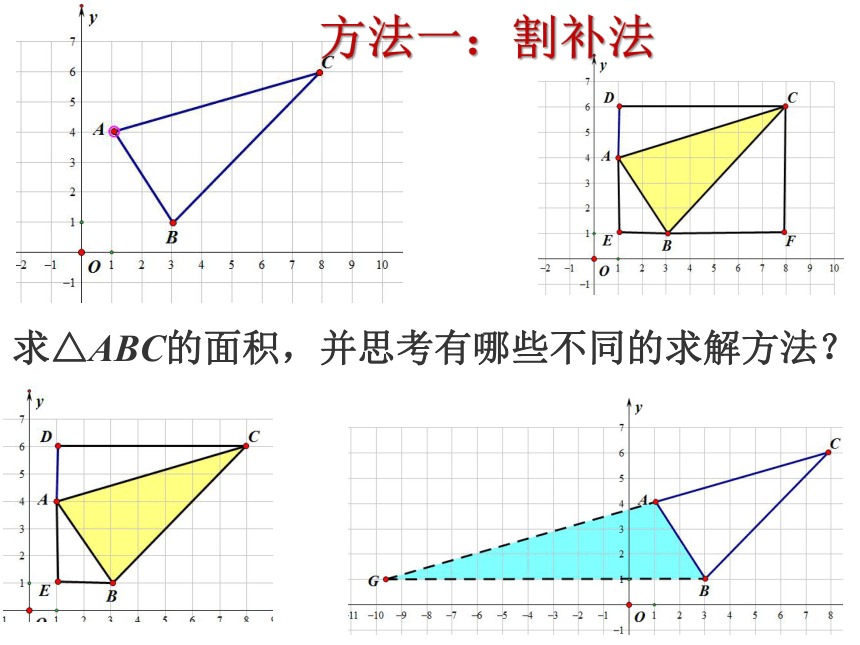
求△ABC的面积,并思考有哪些不同的求解方法?
方法一:割补法
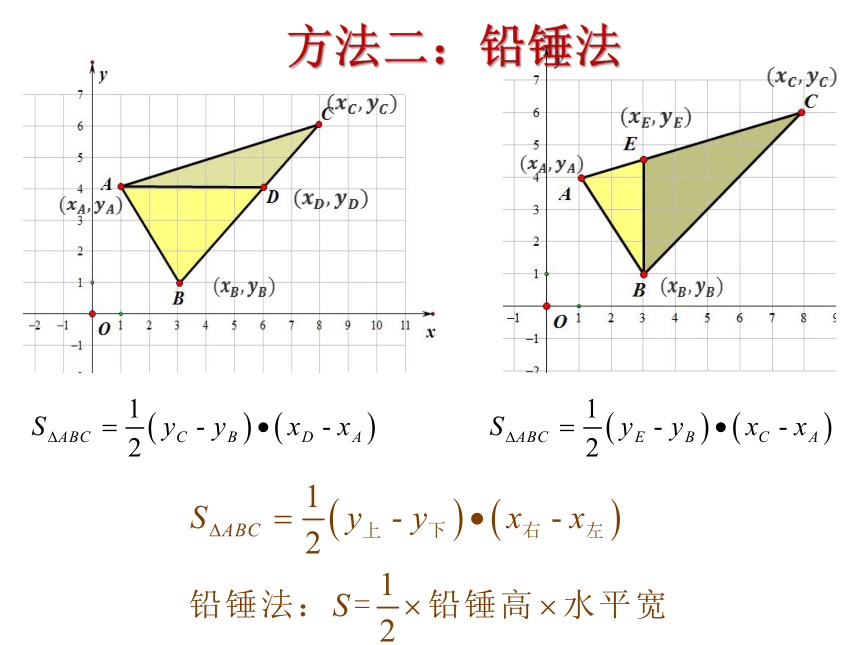
方法二:铅锤法
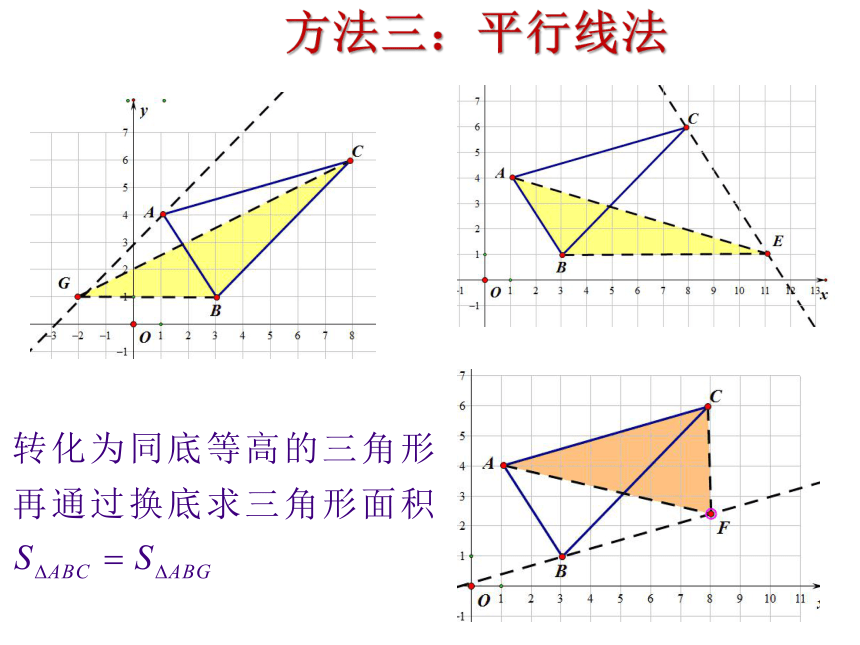
方法三:平行线法
坐标系中求三角形面积的主要方法
直接求解:
公式法:S = ×底×高
(优先选择在坐标轴上或者平行于坐标轴的边作为三角形的底)
间接求解:
割补法:将三角形分割或者补全为方便求面积的图形
铅垂法:S = ×铅垂高×水平宽(适用于任意三点)
平行线法:利用平行线将不能直接求的三角形的面积转化
为能直接求解的三角形的面积
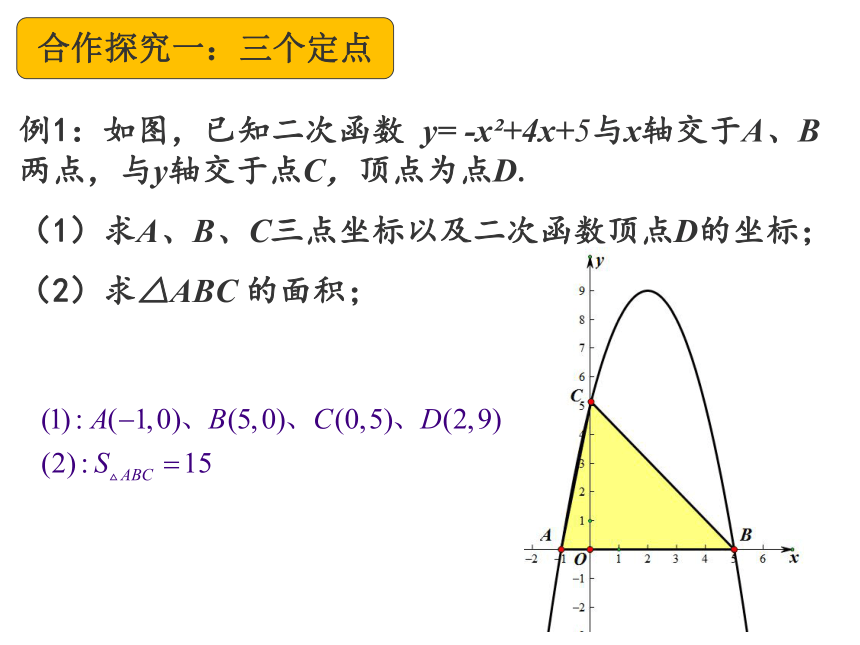
例1:如图,已知二次函数 y= -x +4x+5与x轴交于A、B两点,与y轴交于点C,顶点为点D.
(1)求A、B、C三点坐标以及二次函数顶点D的坐标;
(2)求△ABC 的面积;
合作探究一:三个定点
变式:请求出△BCD的面积,你有哪些不同的求解方法?
变式:请求出△BCD的面积,你有哪些不同的求解方法?
例2:若在x轴上方的二次函数图像上存在点E,使得△ABE面积与△ABC面积相等,求E点坐标.
合作探究二:两定一动
E(4,5)
变式:若在x轴上方的二次函数图像上存在一动点E,使得△BCE面积与△ABC面积相等,求E点坐标.
合作探究二:两定一动
E1(2,9)、E2(3,8)
y= -x+11
y= -x-1
y= -x+5
若二次函数上有一动点E从点C出发沿二次函数运动到点B,在运动的过程中△BCE面积大小是如何变化的?求△BCE面积的最大值.
拓展延伸
求二次函数中三角形面积的主要方法
直接求解:
公式法:S = ×底×高(优先选择坐标轴边为底)
间接求解:
割补法:将三角形分割或者补全为方便求面积的图形
铅垂法:S = ×水平宽×铅垂高(适用于任意三点)
平移法:利用平行线将不能直接求的三角形的面积转化
为能直接求解的三角形的面积
1.如图,在平面直角系中,已知二次函数与x轴相交于点A(-3, 0)B(1, 0),与y轴相交于点C(0, 3),过点C作CD//x轴交二次函数于点 D.
(1)求该二次函数的表达式;
(2)连接AC、BC,求ΔABC的面积
(3)点E(-4,-5)是二次函数上一点,求ΔCDE的面积
(4)点M是二次函数的顶点,求ΔACM的面积
(5)点P是第二象限内该二次函数上的一动点,当点P运动到什么位置时,ΔACP的面积最大?求出此时点P的坐标和ΔACP的最大面积
课后作业
二次函数与三角形面积
近几年成都中考二次函数与三角形面积考点
近几年成都中考二次函数与三角形面积考点
坐标三角形
知识回顾
请计算:
求△ABC的面积,并思考有哪些不同的求解方法?
方法一:割补法
方法二:铅锤法
方法三:平行线法
坐标系中求三角形面积的主要方法
直接求解:
公式法:S = ×底×高
(优先选择在坐标轴上或者平行于坐标轴的边作为三角形的底)
间接求解:
割补法:将三角形分割或者补全为方便求面积的图形
铅垂法:S = ×铅垂高×水平宽(适用于任意三点)
平行线法:利用平行线将不能直接求的三角形的面积转化
为能直接求解的三角形的面积
例1:如图,已知二次函数 y= -x +4x+5与x轴交于A、B两点,与y轴交于点C,顶点为点D.
(1)求A、B、C三点坐标以及二次函数顶点D的坐标;
(2)求△ABC 的面积;
合作探究一:三个定点
变式:请求出△BCD的面积,你有哪些不同的求解方法?
变式:请求出△BCD的面积,你有哪些不同的求解方法?
例2:若在x轴上方的二次函数图像上存在点E,使得△ABE面积与△ABC面积相等,求E点坐标.
合作探究二:两定一动
E(4,5)
变式:若在x轴上方的二次函数图像上存在一动点E,使得△BCE面积与△ABC面积相等,求E点坐标.
合作探究二:两定一动
E1(2,9)、E2(3,8)
y= -x+11
y= -x-1
y= -x+5
若二次函数上有一动点E从点C出发沿二次函数运动到点B,在运动的过程中△BCE面积大小是如何变化的?求△BCE面积的最大值.
拓展延伸
求二次函数中三角形面积的主要方法
直接求解:
公式法:S = ×底×高(优先选择坐标轴边为底)
间接求解:
割补法:将三角形分割或者补全为方便求面积的图形
铅垂法:S = ×水平宽×铅垂高(适用于任意三点)
平移法:利用平行线将不能直接求的三角形的面积转化
为能直接求解的三角形的面积
1.如图,在平面直角系中,已知二次函数与x轴相交于点A(-3, 0)B(1, 0),与y轴相交于点C(0, 3),过点C作CD//x轴交二次函数于点 D.
(1)求该二次函数的表达式;
(2)连接AC、BC,求ΔABC的面积
(3)点E(-4,-5)是二次函数上一点,求ΔCDE的面积
(4)点M是二次函数的顶点,求ΔACM的面积
(5)点P是第二象限内该二次函数上的一动点,当点P运动到什么位置时,ΔACP的面积最大?求出此时点P的坐标和ΔACP的最大面积
课后作业
同课章节目录
