2024-2025学年北师大版九年级数学下册课件:1.3 三角函数的计算(共32张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册课件:1.3 三角函数的计算(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
第一章 直角三角形的边角关系
1.3 三角函数的计算
1.学会利用计算器求三角函数值并进行相关计算. (重点)
2.学会利用计算器根据三角函数值求锐角度数并计算.(难点)
学习目标
新课导入
在Rt△ABC中,∠ACB=90°,BC=ABsin 16°.你知
道sin16°是多少吗?我们可以借助科学计算器求锐角的三
角函数值. 怎样用科学计算器求三角函数值呢?
新课讲解
知识点1 用计算器求锐角的三角函数值
计算器的使用方法:
(1)求整数度数的锐角三角函数值,在科学计算器的面
板上涉及三角函数的键有 当我们
计算整数度数的某锐角的三角函数值时,可选按这
三个键之一,然后再从高位到低位依次按出表示度
数的键,然后按 键,屏幕上就会显示出结果.
新课讲解
(2)求非整数度数的锐角三角函数值,若度数的单位是用度表示的,则按整数度数的按键步骤操作即可 .
若度数的单位是用度、分、秒表示的,在用科学计算器计算三角函数值时,同样先按
然后依次按 (度) 最后按
键,屏幕上就会显示出结果 . 若锐角中只有度、秒,则应在 (分)键前补上 0.
新课讲解
例
1. 用计算器计算:(结果精确到万分位)
(1)sin 26°≈ ;
(2) sin82°48′15″≈________.
0.4384
0.9921
分析:已知锐角求三角函数值,按照正确的按键顺序按键,将屏幕显示的结果按要求取近似值即可.
新课讲解
例
典例分析
2. 已知在Rt△ABC中,∠C=90°,若∠A=23°,斜
边c=14,求∠A的对边a的长.(结果精确到0.01).
分析:c是斜边,而a是∠A的对边,故可利用∠A的正弦求a.
解:由sin A= 则a=c·sin A=14sin 23°,利用计算器计算得a≈5.47.
新课讲解
练一练
1 用计算器求下列各式的值:
(1) sin 56°; (2) cos 20.5°;
(3 ) tan 44°59'59"; (4) sin 15°+ cos 61°+ tan 76°.
解:
(1) sin 56°≈0.829 0;
(2) cos 20.5°≈0.936 7;
(3) tan 44°59′59″≈1.000 0;
(4) sin 15°+cos 61°+tan 76°≈4.754 4.
新课讲解
知识点2 已知锐角的三角函数值,用计算器求锐角
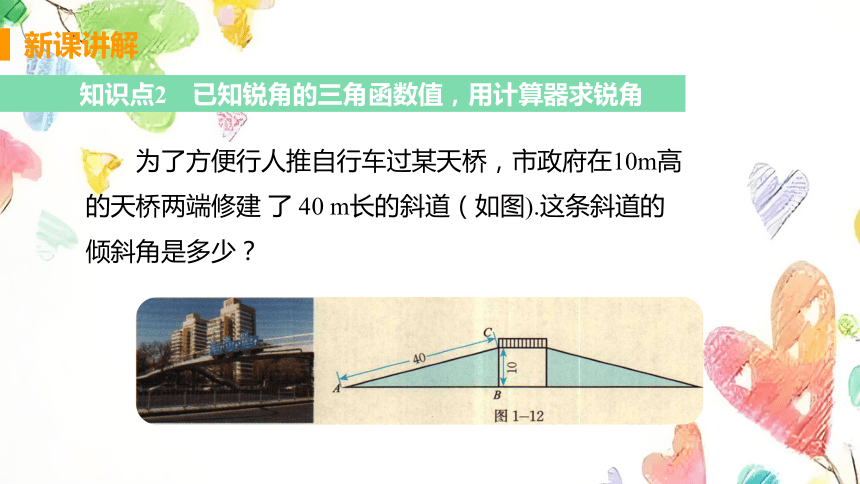
为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修建 了 40 m长的斜道(如图).这条斜道的倾斜角是多少?
新课讲解
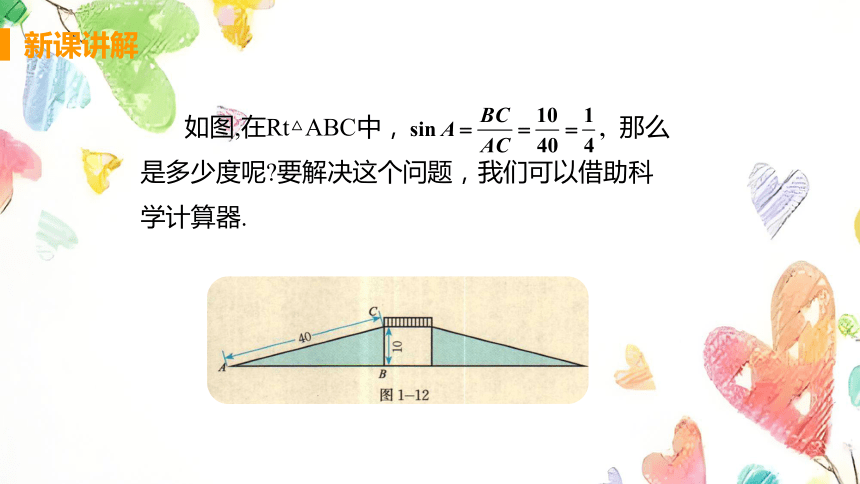
如图,在Rt△ABC中, 那么是多少度呢 要解决这个问题,我们可以借助科学计算器.
新课讲解
1.已知三角函数值,用计算器求角度,需要用到sin ,
cos ,tan 键的第二功能“sin-1,cos-1,tan-1”和
SHIFT 键.
2.具体操作步骤是:先按SHIFT 键,再按sin ,cos ,
tan 键之一,再依次输入三角函数值,最后按=键,
则屏幕上就会显示出结果.
新课讲解
例
典例分析
3. 根据下列条件求锐角 A 的度数:
(1) sin A=0.921 6;
(2) cos A=0.680 7;
(3) tan A=0.189 0.
分析:按计算器的使用说明依次按键 .
新课讲解
解:(1) 按键顺序为:
显示结果为 sin-10.921 6=67.161 123 32,再按 得∠ A ≈ 67° 9′ 40″ .
(2)按按键顺序为:
显示结果为 cos-10.680 7=47.101 632 24,
再按 得∠ A ≈ 47° 6′ 6″ .
(3)按键顺序为:
显示结果为 tan-10.189 0=10.702 657 49,
再按 得∠ A ≈ 10° 42′ 10″ .
新课讲解
练一练
1 已知sin θ = 0.829 04,求锐角θ的度数.
解:
∵sin θ=0.829 04,∴θ≈56°0′1″.
2 一梯子斜靠在一面墙上 已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m, 求梯子与地面所成锐角的度数.
解:
设梯子与地面所成的锐角为∠α,
则cos α= = =0.625.
∴∠α≈51°19′4″.
所以,梯子与地面所成的锐角的度数约为51°19′4″.
课堂小结
1.利用计算器可求锐角的三角函数值,按键顺序为:
先按 键或 键或 键,再按角度值,
最后按 键就可求出相应的三角函数值.
2.已知锐角三角函数值也可求相应的锐角,按键顺
序为:先按 键,再按 键或 键或
键,然后输入三角函数值,最后按 键
就可求出相应角度.
sin
sin
cos
cos
tan
tan
2nd F
=
=
当堂小练
1.为了方便行人推车过某天桥,市政府在10 m高的天桥一侧修建了40 m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A. 2ndF sin 0 · 2 5 =
B. Sin 2ndF 0 · 2 5 =
C. sin 0 · 2 5 =
D. 2ndF cos 0 · 2 5 =
A
当堂小练
2.已知sin α= ,求α,若用科学计算器计算且结果以“度、分、秒”为单位,最后按键( )
A.AC/ON B. SHIFT
C.MODE D. °′ ″
D
用计算器求非特殊角的三角函数值
1.(北师9下P15改编、人教9下P68改编)使用计算器求下列三角函数值(结果精确到0.001).
(1)sin 32°≈ ;
(2)cos 27.35°≈ ;
(3)tan 30°30'30″≈ ;
(4)sin 20°-cos 20°≈ .
-0.598
0.589
0.888
0.530
用计算器求非特殊锐角的度数
2.(北师9下P15改编、人教9下P68改编)已知锐角α的三角函数值,使用计算器求锐角α的度数.
(1)sin α=0.25,则α= ° ';
(2)cos α=0.8,则α= ° ';
(3)tan α=2.4,则α= ° '.
23
67
52
36
29
14
三角函数的实际应用
在实际问题中,要善于运用数学核心素养中的“数学建模”思想,把实际问题转化为直角三角形中的边角关系加以解决.
3.(北师9下P14改编)如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD约为 米(结果精确到0.1米).
1.6
4.【例1】用科学计算器求sin 24°的值,以下按键顺序正确的是( )
A
5.【例2】用计算器求sin 62°20'的值,正确的是( )
A.0.885 7 B.0.885 6
C.0.885 2 D.0.885 1
A
6.【例3】(跨学科融合)在滑轮的牵引下,一辆小车沿着如图所示的斜坡向上行驶了100 m,其铅直高度上升了15 m,则坡角α的度数为 .(结果精确到0.1°)
8.6°
7.【例4】(北师9下P15、人教9下P75)如图,物华大厦离小伟家60 m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1 m).
解:如图,AE=BD=60 m.
在Rt△AEC中,∠CAE=45°,
∴CE=AE=60 m.
在Rt△AED中,
ED=AE·tan 37°≈60×0.754≈45.2(m).
∴CD=CE+ED≈60+45.2=105.2(m).
答:该大厦的高度约为105.2 m.
答案图
8.用计算器求tan A=0.523 4中锐角A的度数的按键顺序正确的是( )
C
9.用计算器求sin 20°+tan 54°33'的结果等于(结果精确到0.01)( )
A.2.25 B.1.55
C.1.73 D.1.75
D
10.如图,在距离树底部10 m的A处,测得大树顶端C的仰角∠BAC=50°,则这棵树的高度BC是 m.(结果精确到0.1 m)
11.9
★11. 0.55 (北师9下P26改编、人教9下P84)如图,两座建筑物的水平距离BC为40 m,从A点测得D点的俯角α为45°,测得C点的俯角β为60°.求这两座建筑物AB,CD的高度(结果保留小数点后一位,1.414,1.732).
解:如图,延长CD,交AE于点E,可得DE⊥AE,
在Rt△AED中,∵∠EAD=45°,
∴AE=DE=BC=40 m.
在Rt△ABC中,∠BAC=90°-60°=30°,BC=40 m,
∴AB=40 69.3 m.∴CD=EC-ED=AB-ED≈69.3-40=29.3 m.
答:这两座建筑物AB,CD的高度分别为69.3 m和29.3 m.
请完成本节对应习题
布置作业
第一章 直角三角形的边角关系
1.3 三角函数的计算
1.学会利用计算器求三角函数值并进行相关计算. (重点)
2.学会利用计算器根据三角函数值求锐角度数并计算.(难点)
学习目标
新课导入
在Rt△ABC中,∠ACB=90°,BC=ABsin 16°.你知
道sin16°是多少吗?我们可以借助科学计算器求锐角的三
角函数值. 怎样用科学计算器求三角函数值呢?
新课讲解
知识点1 用计算器求锐角的三角函数值
计算器的使用方法:
(1)求整数度数的锐角三角函数值,在科学计算器的面
板上涉及三角函数的键有 当我们
计算整数度数的某锐角的三角函数值时,可选按这
三个键之一,然后再从高位到低位依次按出表示度
数的键,然后按 键,屏幕上就会显示出结果.
新课讲解
(2)求非整数度数的锐角三角函数值,若度数的单位是用度表示的,则按整数度数的按键步骤操作即可 .
若度数的单位是用度、分、秒表示的,在用科学计算器计算三角函数值时,同样先按
然后依次按 (度) 最后按
键,屏幕上就会显示出结果 . 若锐角中只有度、秒,则应在 (分)键前补上 0.
新课讲解
例
1. 用计算器计算:(结果精确到万分位)
(1)sin 26°≈ ;
(2) sin82°48′15″≈________.
0.4384
0.9921
分析:已知锐角求三角函数值,按照正确的按键顺序按键,将屏幕显示的结果按要求取近似值即可.
新课讲解
例
典例分析
2. 已知在Rt△ABC中,∠C=90°,若∠A=23°,斜
边c=14,求∠A的对边a的长.(结果精确到0.01).
分析:c是斜边,而a是∠A的对边,故可利用∠A的正弦求a.
解:由sin A= 则a=c·sin A=14sin 23°,利用计算器计算得a≈5.47.
新课讲解
练一练
1 用计算器求下列各式的值:
(1) sin 56°; (2) cos 20.5°;
(3 ) tan 44°59'59"; (4) sin 15°+ cos 61°+ tan 76°.
解:
(1) sin 56°≈0.829 0;
(2) cos 20.5°≈0.936 7;
(3) tan 44°59′59″≈1.000 0;
(4) sin 15°+cos 61°+tan 76°≈4.754 4.
新课讲解
知识点2 已知锐角的三角函数值,用计算器求锐角
为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修建 了 40 m长的斜道(如图).这条斜道的倾斜角是多少?
新课讲解
如图,在Rt△ABC中, 那么是多少度呢 要解决这个问题,我们可以借助科学计算器.
新课讲解
1.已知三角函数值,用计算器求角度,需要用到sin ,
cos ,tan 键的第二功能“sin-1,cos-1,tan-1”和
SHIFT 键.
2.具体操作步骤是:先按SHIFT 键,再按sin ,cos ,
tan 键之一,再依次输入三角函数值,最后按=键,
则屏幕上就会显示出结果.
新课讲解
例
典例分析
3. 根据下列条件求锐角 A 的度数:
(1) sin A=0.921 6;
(2) cos A=0.680 7;
(3) tan A=0.189 0.
分析:按计算器的使用说明依次按键 .
新课讲解
解:(1) 按键顺序为:
显示结果为 sin-10.921 6=67.161 123 32,再按 得∠ A ≈ 67° 9′ 40″ .
(2)按按键顺序为:
显示结果为 cos-10.680 7=47.101 632 24,
再按 得∠ A ≈ 47° 6′ 6″ .
(3)按键顺序为:
显示结果为 tan-10.189 0=10.702 657 49,
再按 得∠ A ≈ 10° 42′ 10″ .
新课讲解
练一练
1 已知sin θ = 0.829 04,求锐角θ的度数.
解:
∵sin θ=0.829 04,∴θ≈56°0′1″.
2 一梯子斜靠在一面墙上 已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m, 求梯子与地面所成锐角的度数.
解:
设梯子与地面所成的锐角为∠α,
则cos α= = =0.625.
∴∠α≈51°19′4″.
所以,梯子与地面所成的锐角的度数约为51°19′4″.
课堂小结
1.利用计算器可求锐角的三角函数值,按键顺序为:
先按 键或 键或 键,再按角度值,
最后按 键就可求出相应的三角函数值.
2.已知锐角三角函数值也可求相应的锐角,按键顺
序为:先按 键,再按 键或 键或
键,然后输入三角函数值,最后按 键
就可求出相应角度.
sin
sin
cos
cos
tan
tan
2nd F
=
=
当堂小练
1.为了方便行人推车过某天桥,市政府在10 m高的天桥一侧修建了40 m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A. 2ndF sin 0 · 2 5 =
B. Sin 2ndF 0 · 2 5 =
C. sin 0 · 2 5 =
D. 2ndF cos 0 · 2 5 =
A
当堂小练
2.已知sin α= ,求α,若用科学计算器计算且结果以“度、分、秒”为单位,最后按键( )
A.AC/ON B. SHIFT
C.MODE D. °′ ″
D
用计算器求非特殊角的三角函数值
1.(北师9下P15改编、人教9下P68改编)使用计算器求下列三角函数值(结果精确到0.001).
(1)sin 32°≈ ;
(2)cos 27.35°≈ ;
(3)tan 30°30'30″≈ ;
(4)sin 20°-cos 20°≈ .
-0.598
0.589
0.888
0.530
用计算器求非特殊锐角的度数
2.(北师9下P15改编、人教9下P68改编)已知锐角α的三角函数值,使用计算器求锐角α的度数.
(1)sin α=0.25,则α= ° ';
(2)cos α=0.8,则α= ° ';
(3)tan α=2.4,则α= ° '.
23
67
52
36
29
14
三角函数的实际应用
在实际问题中,要善于运用数学核心素养中的“数学建模”思想,把实际问题转化为直角三角形中的边角关系加以解决.
3.(北师9下P14改编)如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD约为 米(结果精确到0.1米).
1.6
4.【例1】用科学计算器求sin 24°的值,以下按键顺序正确的是( )
A
5.【例2】用计算器求sin 62°20'的值,正确的是( )
A.0.885 7 B.0.885 6
C.0.885 2 D.0.885 1
A
6.【例3】(跨学科融合)在滑轮的牵引下,一辆小车沿着如图所示的斜坡向上行驶了100 m,其铅直高度上升了15 m,则坡角α的度数为 .(结果精确到0.1°)
8.6°
7.【例4】(北师9下P15、人教9下P75)如图,物华大厦离小伟家60 m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1 m).
解:如图,AE=BD=60 m.
在Rt△AEC中,∠CAE=45°,
∴CE=AE=60 m.
在Rt△AED中,
ED=AE·tan 37°≈60×0.754≈45.2(m).
∴CD=CE+ED≈60+45.2=105.2(m).
答:该大厦的高度约为105.2 m.
答案图
8.用计算器求tan A=0.523 4中锐角A的度数的按键顺序正确的是( )
C
9.用计算器求sin 20°+tan 54°33'的结果等于(结果精确到0.01)( )
A.2.25 B.1.55
C.1.73 D.1.75
D
10.如图,在距离树底部10 m的A处,测得大树顶端C的仰角∠BAC=50°,则这棵树的高度BC是 m.(结果精确到0.1 m)
11.9
★11. 0.55 (北师9下P26改编、人教9下P84)如图,两座建筑物的水平距离BC为40 m,从A点测得D点的俯角α为45°,测得C点的俯角β为60°.求这两座建筑物AB,CD的高度(结果保留小数点后一位,1.414,1.732).
解:如图,延长CD,交AE于点E,可得DE⊥AE,
在Rt△AED中,∵∠EAD=45°,
∴AE=DE=BC=40 m.
在Rt△ABC中,∠BAC=90°-60°=30°,BC=40 m,
∴AB=40 69.3 m.∴CD=EC-ED=AB-ED≈69.3-40=29.3 m.
答:这两座建筑物AB,CD的高度分别为69.3 m和29.3 m.
请完成本节对应习题
布置作业
