2025年湖北省中考数学复习专题二 统计(共21张PPT)
文档属性
| 名称 | 2025年湖北省中考数学复习专题二 统计(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 315.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 16:31:18 | ||
图片预览






文档简介
(共21张PPT)
题型二 统 计
2025湖北数学
1. 跳绳是我国的民间传统体育项目,它既可以促进青少年的健康发育,又可以培养身体的平衡感.某校为了解七年级学生的跳绳情况,举办了一场1分钟跳绳测试(每分钟不低于172个为满分).从中随机抽取20名学生的测试成绩,并进行收集,整理与分析:
数据收集:
150,199,160,152,182,162,176,194,182,178,151,175,161,163,167,179,182,185,192,198
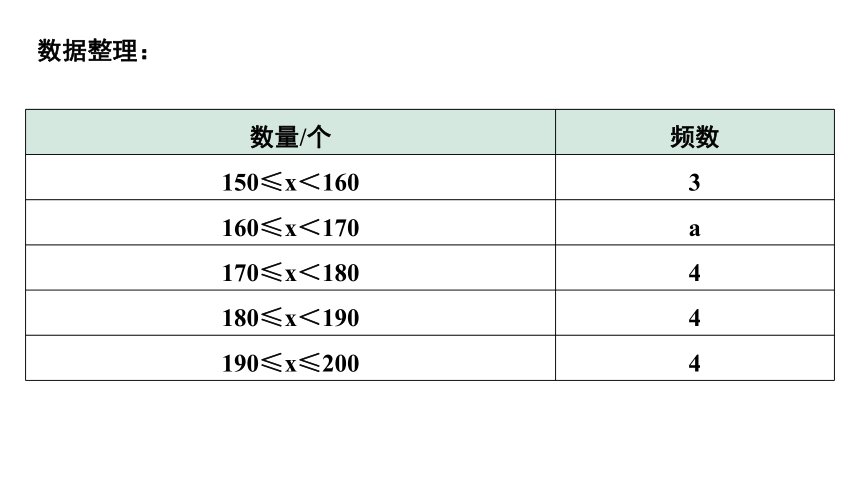
数据整理:
数量/个 频数
150≤x<160 3
160≤x<170 a
170≤x<180 4
180≤x<190 4
190≤x≤200 4
问题解决:
(1)填空:a=____,b=____,c=____;
(2)若七年级共有800人参加了跳绳测试,估计在本次测试中获得满分的七年级学生人数;
数据分析:
平均数 众数 中位数
174.4 b c
5
182
177
(2)由题意,参加跳绳测试获得满分的人数有12人,∴800×=480(人),
答:估计在本次测试中获得满分的七年级学生有480人;
(3)小敏同学1分钟跳了175个,她认为自己的成绩高于平均数,所以她的成绩超过了一半的同学.判断小敏同学的说法是否正确,并说明理由.
数据分析:
平均数 众数 中位数
174.4 182 177
(3)不正确,理由:小敏的成绩虽然高于平均数,但小于中位数177,因此她的成绩没有超过一半的同学,
∴小敏同学的说法不正确.
2. 为深入学习贯彻党的二十大精神,落实中共中央办公厅、国务院办公厅《关于实施中华优秀传统文化传承发展工程的意见》和全国、全省语言文字会议精神,坚定历史自信、文化自信,在全社会掀起亲近经典、学习诗词的热潮,某校决定举办“诗词大赛”.在一轮比赛中有30名参赛者参加诗词积累、诗词运用,该校对他们的这两项成绩(百分制)分别进行了整理和分析(A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x≤100),部分信息如下:
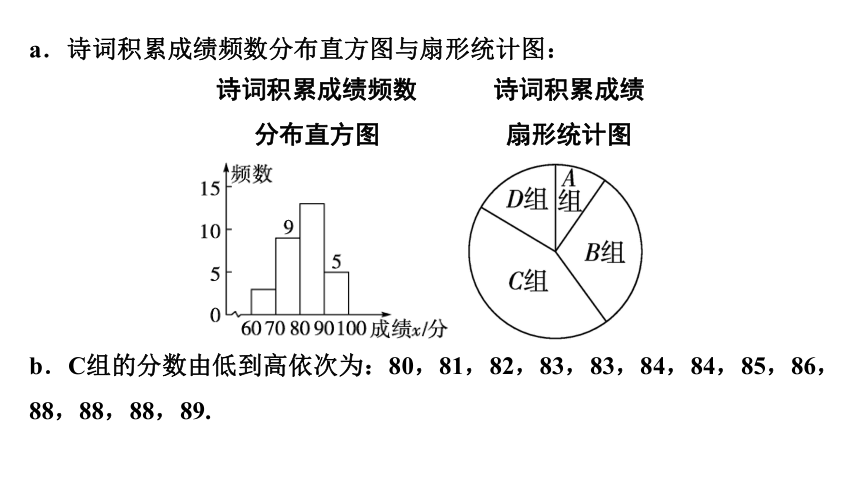
a.诗词积累成绩频数分布直方图与扇形统计图:
b.C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
诗词积累成绩频数 诗词积累成绩
分布直方图 扇形统计图
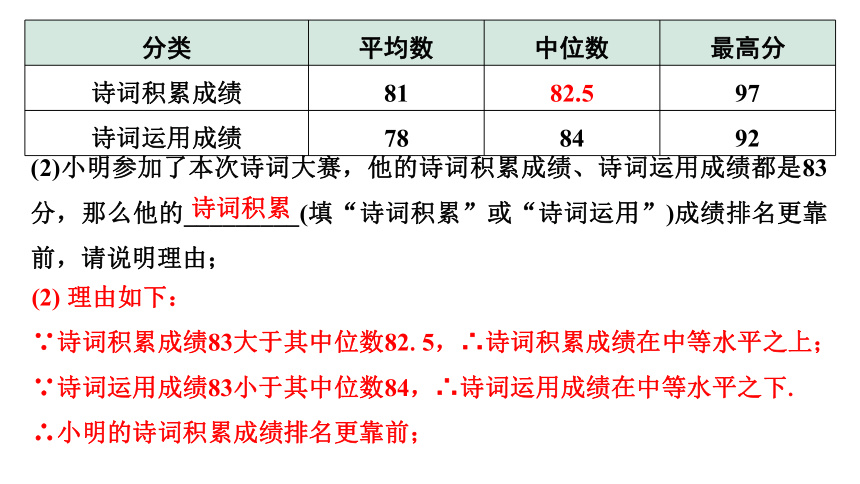
c.诗词积累、诗词运用成绩的平均数、中位数、最高分如下表:
根据以上信息,回答下列问题:
(1)表格中m=______,扇形统计图中,C组对应扇形的圆心角的度数为_____;
分类 平均数 中位数 最高分
诗词积累成绩 81 m 97
诗词运用成绩 78 84 92
156°
82.5
分类 平均数 中位数 最高分
诗词积累成绩 81 82.5 97
诗词运用成绩 78 84 92
(2)小明参加了本次诗词大赛,他的诗词积累成绩、诗词运用成绩都是83分,那么他的_________(填“诗词积累”或“诗词运用”)成绩排名更靠前,请说明理由;
(2) 理由如下:
∵诗词积累成绩83大于其中位数82.5,∴诗词积累成绩在中等水平之上;
∵诗词运用成绩83小于其中位数84,∴诗词运用成绩在中等水平之下.
∴小明的诗词积累成绩排名更靠前;
诗词积累
(3)请从平均数的角度,分析该校学生诗词积累和诗词运用的情况,并提出合理化建议.
分类 平均数 中位数 最高分
诗词积累成绩 81 82.5 97
诗词运用成绩 78 84 92
(3)从平均数来看,该校学生诗词运用的平均水平要比诗词积累的平均水平低;
建议:该校应多开展诗词比赛等活动,锻炼学生诗词运用的能力.(答案不唯一,合理即可)
3. 某地文旅局为了更好地促进本地旅游业的发展,将A,B两家景点的相关资料放在网络平台上进行宣传,邀请曾在这两家景点均游览过的游客参与调研,从自然景观、人文历史、设施服务三个方面对这两家景点进行“满意度”评分(满分100分).现从这两家景点“满意度”评分中各随机抽取10个评分数据,并对所得数据进行整理,分析,描述:
Ⅰ.A,B两家景点“满意度”评分折线统计图:
Ⅱ.A,B两家景点“满意度”评分的平均数,中位数,众数如下表:
根据以上信息,解答下列问题:
(1)表中a的值是____,b的值是____;
— 平均数 中位数 众数
A景点 a 95 95
B景点 95 b 97
97
95
(2)据统计,某季度在B景点游览的人数为30 000,请估计该季度B景点评分在95分以上的人数;
(2)由题图可得,B景点10个评分数据中有6个大于95分,
∴30 000×=18 000(人),
答:估计该季度B景点评分在95分以上的人数为18 000人;
(3)根据“满意度”的评分情况,该文旅局打算将A,B两家景点中的一家置顶推荐,你认为该文旅局会将这两家景点中的哪家置顶推荐?请说明理由(至少从一个方面说明).
(3)选择B景点置顶推荐.理由:A,B两家景点“满意度”评分的平均数相同,B景点“满意度”评分的中位数比A景点“满意度”评分的中位数高;或A,B两家景点“满意度”评分的平均数相同,B景点“满意度”评分的众数比A景点“满意度”评分的众数高.(答案不唯一,合理即可)
— 平均数 中位数 众数
A景点 95 95 95
B景点 95 97 97
4. 春季新学期开学以来,某校积极响应国家号召,开设了劳动教育实践课,七年级(1)班的实践课任务是种植白菜.课程期间,该班级成功种植白菜500颗.为了估计这批白菜的总质量,等白菜成熟后,七年级(1)班同学随机拔取了20颗白菜,分别称得其质量(精确到0.1千克).现将拔取的20颗白菜的质量作为样本,绘制出如下不完整的统计图表:
被拔取白菜质量统计表
平均数 众数 中位数
2.0 a b
请根据以上信息,解答下列问题:
(1)直接写出表格中a,b的值;
被拔取白菜质量统计表
平均数 众数 中位数
2.0 a b
(1)a=1.9,b=2.0
(2)课程结束后,学校食堂统一回收实践课程期间种植的全部蔬菜,其中白菜的回收价为每千克1.75元,请估计这500颗白菜能卖多少元;
平均数 众数 中位数
2.0 1.9 2.0
(2)由表格知,被拔取白菜质量的平均数为2.0千克,
∴2.0×500×1.75=1 750(元),
答:估计这500颗白菜能卖1 750元;
(3)请从平均数,众数,中位数中选择一个统计量,结合本题解释它的意义
平均数 众数 中位数
2.0 1.9 2.0
(3)从中位数看,被拔取的白菜有一半的质量大于等于2.0千克;或从众数看,被拔取的20颗白菜中质量为1.9千克的白菜颗数最多.(答案不唯一,合理即可)
5. 近年来,人工智能领域技术不断突破,创新成果逐渐融入社会各个领域,深刻改变着人们的日常工作、生活方式,有关人员开展了A,B两款AI机器人使用满意度的评分问卷调查活动,并从中各随机抽取相同数量的问卷,将收集的数据进行整理后分为四个等级(x为满意度评分):不满意x<70,良好70≤x<80,满意 80≤x<90,非常满意x≥90,部分信息如下:
a.A,B两款AI机器人满意度评分条形统计图:
b.A款AI机器人评分在70≤x<80这一组的具体数据是:78,74,79,75,79,78;
根据以上信息,回答下列问题:
(1)本次抽取的问卷共有____份,A款AI机器人评分的中位数为_____分;
(2)对A款AI机器人感到满意的人数是否超过一半?
78.5
40
(2)由(1)得对A款AI机器人评分的中位数为78.5分,
∵78.5分<80分,
∴对A款AI机器人感到满意的人数未超过一半;
(3)在此次问卷调查活动中,若有300人对B款AI机器人进行评分,请估计此次问卷调查活动中对B款AI机器人非常满意的人数;
(4)根据以上绘制的条形统计图,你能获得哪些信息?(写出一条即可)
(4)从满意度为满意的人数看,人们更喜欢使用
B款AI机器人(答案不唯一,合理即可).
(3)由条形统计图得,在本次抽取的问卷中对B款AI机器人评分为非常满
意的有2份,∴300×=30(人),
答:估计此次问卷调查活动中,对B款AI机器人非常满意的人数为30人;
题型二 统 计
2025湖北数学
1. 跳绳是我国的民间传统体育项目,它既可以促进青少年的健康发育,又可以培养身体的平衡感.某校为了解七年级学生的跳绳情况,举办了一场1分钟跳绳测试(每分钟不低于172个为满分).从中随机抽取20名学生的测试成绩,并进行收集,整理与分析:
数据收集:
150,199,160,152,182,162,176,194,182,178,151,175,161,163,167,179,182,185,192,198
数据整理:
数量/个 频数
150≤x<160 3
160≤x<170 a
170≤x<180 4
180≤x<190 4
190≤x≤200 4
问题解决:
(1)填空:a=____,b=____,c=____;
(2)若七年级共有800人参加了跳绳测试,估计在本次测试中获得满分的七年级学生人数;
数据分析:
平均数 众数 中位数
174.4 b c
5
182
177
(2)由题意,参加跳绳测试获得满分的人数有12人,∴800×=480(人),
答:估计在本次测试中获得满分的七年级学生有480人;
(3)小敏同学1分钟跳了175个,她认为自己的成绩高于平均数,所以她的成绩超过了一半的同学.判断小敏同学的说法是否正确,并说明理由.
数据分析:
平均数 众数 中位数
174.4 182 177
(3)不正确,理由:小敏的成绩虽然高于平均数,但小于中位数177,因此她的成绩没有超过一半的同学,
∴小敏同学的说法不正确.
2. 为深入学习贯彻党的二十大精神,落实中共中央办公厅、国务院办公厅《关于实施中华优秀传统文化传承发展工程的意见》和全国、全省语言文字会议精神,坚定历史自信、文化自信,在全社会掀起亲近经典、学习诗词的热潮,某校决定举办“诗词大赛”.在一轮比赛中有30名参赛者参加诗词积累、诗词运用,该校对他们的这两项成绩(百分制)分别进行了整理和分析(A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x≤100),部分信息如下:
a.诗词积累成绩频数分布直方图与扇形统计图:
b.C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
诗词积累成绩频数 诗词积累成绩
分布直方图 扇形统计图
c.诗词积累、诗词运用成绩的平均数、中位数、最高分如下表:
根据以上信息,回答下列问题:
(1)表格中m=______,扇形统计图中,C组对应扇形的圆心角的度数为_____;
分类 平均数 中位数 最高分
诗词积累成绩 81 m 97
诗词运用成绩 78 84 92
156°
82.5
分类 平均数 中位数 最高分
诗词积累成绩 81 82.5 97
诗词运用成绩 78 84 92
(2)小明参加了本次诗词大赛,他的诗词积累成绩、诗词运用成绩都是83分,那么他的_________(填“诗词积累”或“诗词运用”)成绩排名更靠前,请说明理由;
(2) 理由如下:
∵诗词积累成绩83大于其中位数82.5,∴诗词积累成绩在中等水平之上;
∵诗词运用成绩83小于其中位数84,∴诗词运用成绩在中等水平之下.
∴小明的诗词积累成绩排名更靠前;
诗词积累
(3)请从平均数的角度,分析该校学生诗词积累和诗词运用的情况,并提出合理化建议.
分类 平均数 中位数 最高分
诗词积累成绩 81 82.5 97
诗词运用成绩 78 84 92
(3)从平均数来看,该校学生诗词运用的平均水平要比诗词积累的平均水平低;
建议:该校应多开展诗词比赛等活动,锻炼学生诗词运用的能力.(答案不唯一,合理即可)
3. 某地文旅局为了更好地促进本地旅游业的发展,将A,B两家景点的相关资料放在网络平台上进行宣传,邀请曾在这两家景点均游览过的游客参与调研,从自然景观、人文历史、设施服务三个方面对这两家景点进行“满意度”评分(满分100分).现从这两家景点“满意度”评分中各随机抽取10个评分数据,并对所得数据进行整理,分析,描述:
Ⅰ.A,B两家景点“满意度”评分折线统计图:
Ⅱ.A,B两家景点“满意度”评分的平均数,中位数,众数如下表:
根据以上信息,解答下列问题:
(1)表中a的值是____,b的值是____;
— 平均数 中位数 众数
A景点 a 95 95
B景点 95 b 97
97
95
(2)据统计,某季度在B景点游览的人数为30 000,请估计该季度B景点评分在95分以上的人数;
(2)由题图可得,B景点10个评分数据中有6个大于95分,
∴30 000×=18 000(人),
答:估计该季度B景点评分在95分以上的人数为18 000人;
(3)根据“满意度”的评分情况,该文旅局打算将A,B两家景点中的一家置顶推荐,你认为该文旅局会将这两家景点中的哪家置顶推荐?请说明理由(至少从一个方面说明).
(3)选择B景点置顶推荐.理由:A,B两家景点“满意度”评分的平均数相同,B景点“满意度”评分的中位数比A景点“满意度”评分的中位数高;或A,B两家景点“满意度”评分的平均数相同,B景点“满意度”评分的众数比A景点“满意度”评分的众数高.(答案不唯一,合理即可)
— 平均数 中位数 众数
A景点 95 95 95
B景点 95 97 97
4. 春季新学期开学以来,某校积极响应国家号召,开设了劳动教育实践课,七年级(1)班的实践课任务是种植白菜.课程期间,该班级成功种植白菜500颗.为了估计这批白菜的总质量,等白菜成熟后,七年级(1)班同学随机拔取了20颗白菜,分别称得其质量(精确到0.1千克).现将拔取的20颗白菜的质量作为样本,绘制出如下不完整的统计图表:
被拔取白菜质量统计表
平均数 众数 中位数
2.0 a b
请根据以上信息,解答下列问题:
(1)直接写出表格中a,b的值;
被拔取白菜质量统计表
平均数 众数 中位数
2.0 a b
(1)a=1.9,b=2.0
(2)课程结束后,学校食堂统一回收实践课程期间种植的全部蔬菜,其中白菜的回收价为每千克1.75元,请估计这500颗白菜能卖多少元;
平均数 众数 中位数
2.0 1.9 2.0
(2)由表格知,被拔取白菜质量的平均数为2.0千克,
∴2.0×500×1.75=1 750(元),
答:估计这500颗白菜能卖1 750元;
(3)请从平均数,众数,中位数中选择一个统计量,结合本题解释它的意义
平均数 众数 中位数
2.0 1.9 2.0
(3)从中位数看,被拔取的白菜有一半的质量大于等于2.0千克;或从众数看,被拔取的20颗白菜中质量为1.9千克的白菜颗数最多.(答案不唯一,合理即可)
5. 近年来,人工智能领域技术不断突破,创新成果逐渐融入社会各个领域,深刻改变着人们的日常工作、生活方式,有关人员开展了A,B两款AI机器人使用满意度的评分问卷调查活动,并从中各随机抽取相同数量的问卷,将收集的数据进行整理后分为四个等级(x为满意度评分):不满意x<70,良好70≤x<80,满意 80≤x<90,非常满意x≥90,部分信息如下:
a.A,B两款AI机器人满意度评分条形统计图:
b.A款AI机器人评分在70≤x<80这一组的具体数据是:78,74,79,75,79,78;
根据以上信息,回答下列问题:
(1)本次抽取的问卷共有____份,A款AI机器人评分的中位数为_____分;
(2)对A款AI机器人感到满意的人数是否超过一半?
78.5
40
(2)由(1)得对A款AI机器人评分的中位数为78.5分,
∵78.5分<80分,
∴对A款AI机器人感到满意的人数未超过一半;
(3)在此次问卷调查活动中,若有300人对B款AI机器人进行评分,请估计此次问卷调查活动中对B款AI机器人非常满意的人数;
(4)根据以上绘制的条形统计图,你能获得哪些信息?(写出一条即可)
(4)从满意度为满意的人数看,人们更喜欢使用
B款AI机器人(答案不唯一,合理即可).
(3)由条形统计图得,在本次抽取的问卷中对B款AI机器人评分为非常满
意的有2份,∴300×=30(人),
答:估计此次问卷调查活动中,对B款AI机器人非常满意的人数为30人;
同课章节目录
