余角和补角(2)
图片预览



文档简介
课件21张PPT。探究 合作!西寨初中 胡军芳游戏规则:
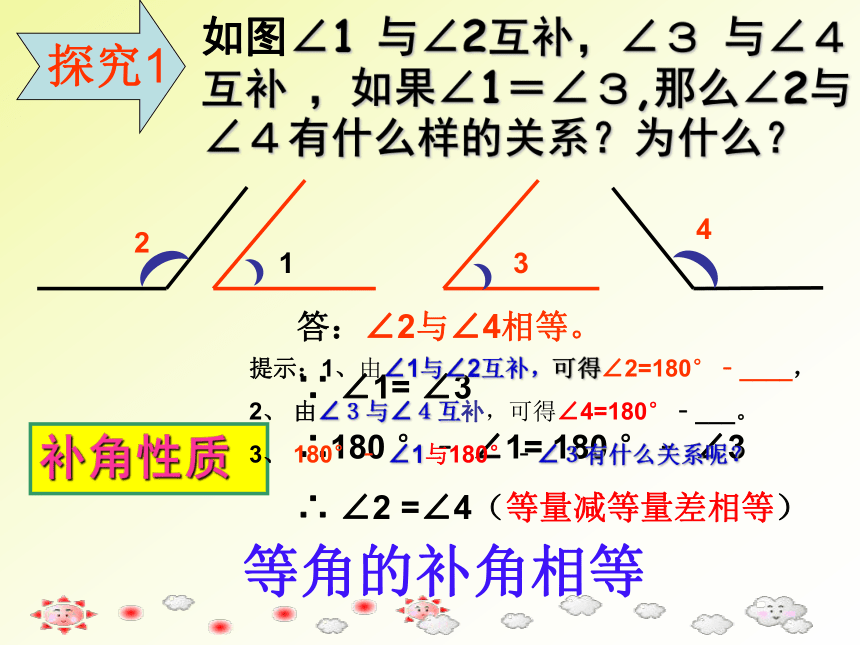
一个同学站起来说出自己角的度数,与他互为余角或互为补角的同学站起来说出自己的度数,其他同学判断他们做得是否正确。如果正确,给他们鼓掌;如果不正确,大家一起纠正。§4.3.3 余角和补角(2)如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4有什么样的关系?为什么?3答:∠2与∠4相等。
∵ ∠1= ∠3
∴180 °﹣ ∠1= 180 °﹣ ∠3
∴ ∠2 =∠4(等量减等量差相等)
等角的补角相等补角性质提示:1、由∠1与∠2互补,可得∠2=180°﹣____,
2、 由∠3与∠4互补,可得∠4=180°﹣___。
3、 180°﹣ ∠1与180°﹣∠3有什么关系呢?
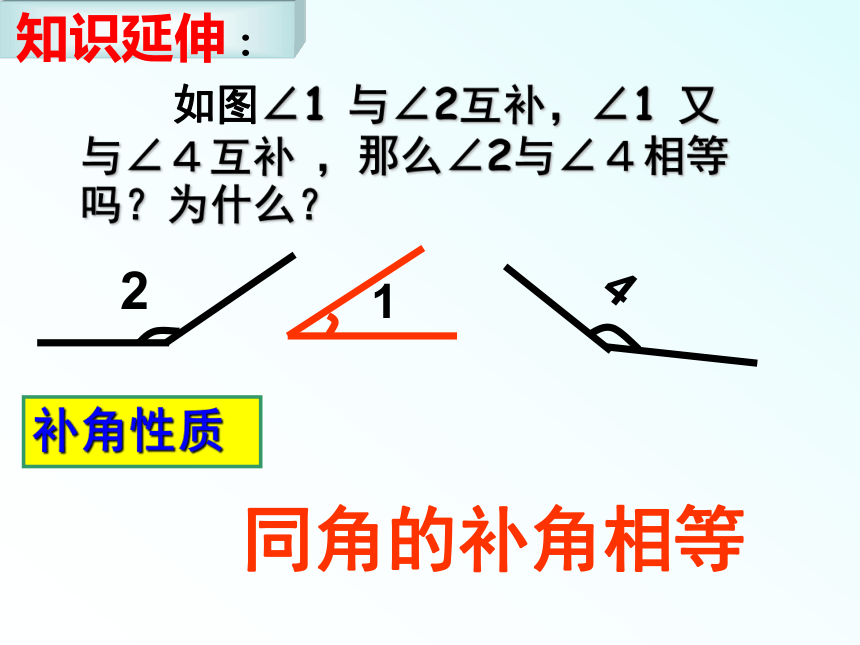
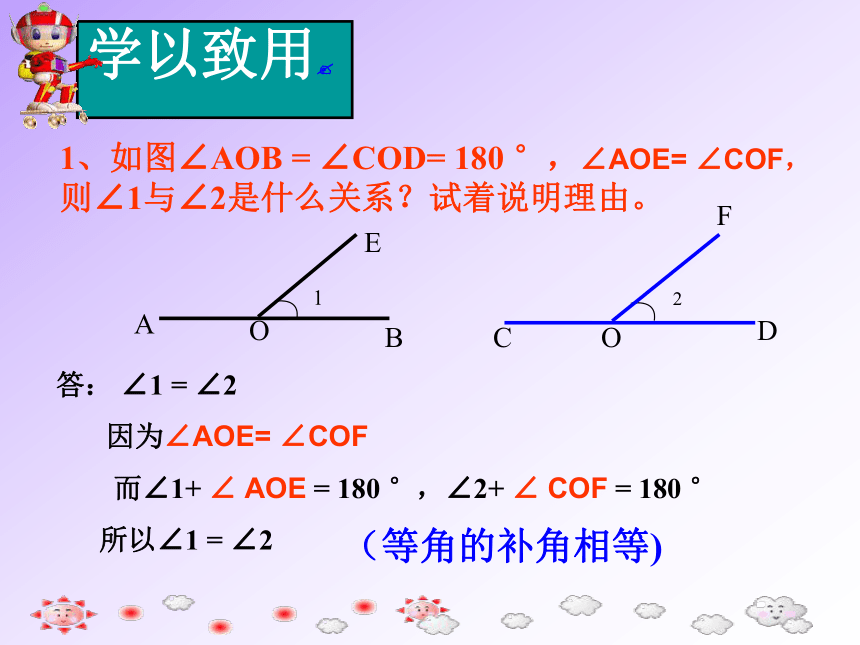
如图∠1 与∠2互补,∠1 又与∠4互补 ,那么∠2与∠4相等吗?为什么?同角的补角相等补角性质1、如图∠AOB = ∠COD= 180 °,∠AOE= ∠COF,则∠1与∠2是什么关系?试着说明理由。答: ∠1 = ∠2
因为∠AOE= ∠COF
而∠1+ ∠ AOE = 180 °,∠2+ ∠ COF = 180 °
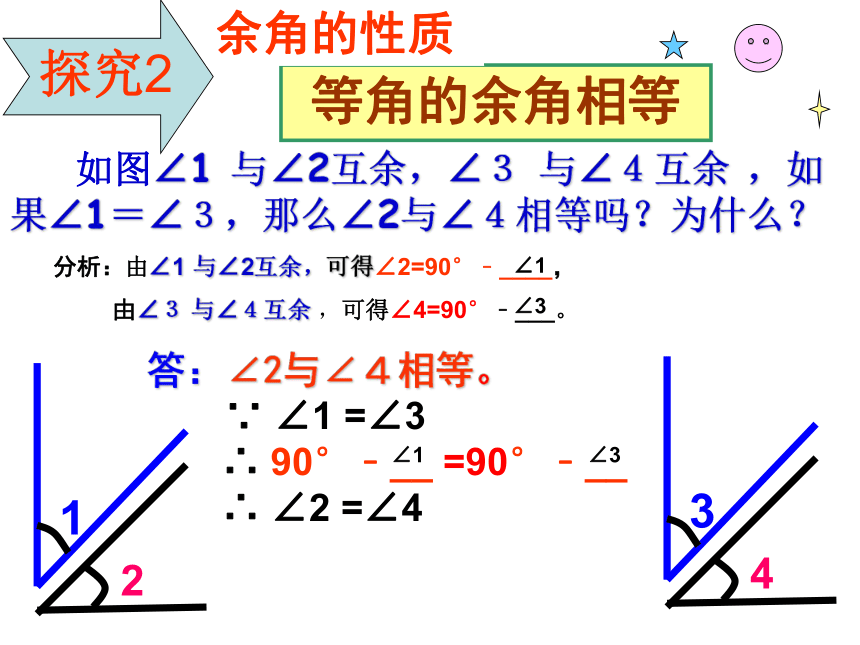
所以∠1 = ∠2(等角的补角相等)AOBCD学以致用? E OF 如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?答:∠2与∠4相等。
∵ ∠1 =∠3
∴ 90°﹣__ =90°﹣__
∴ ∠2 =∠4
等角的余角相等余角的性质分析:由∠1 与∠2互余,可得∠2=90°﹣____,
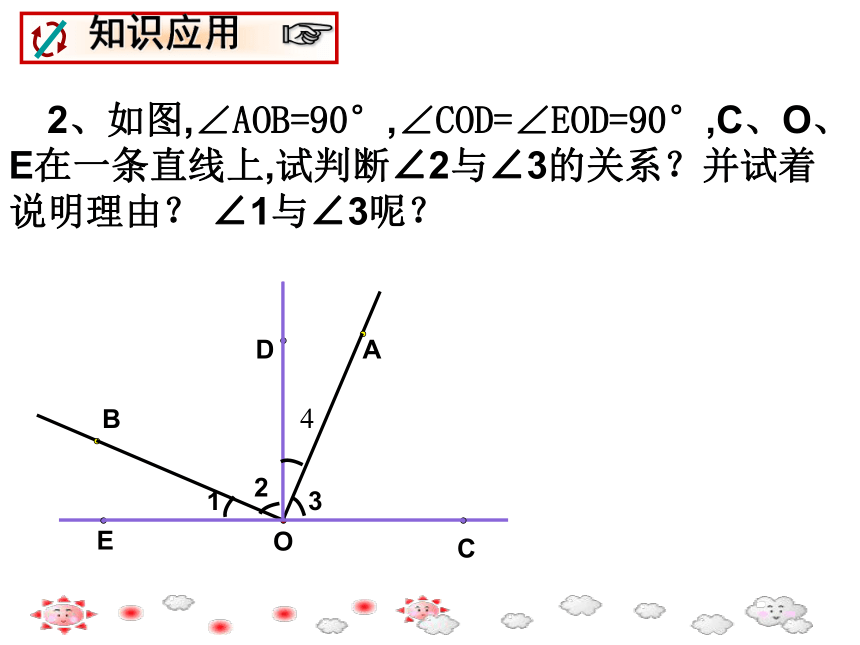
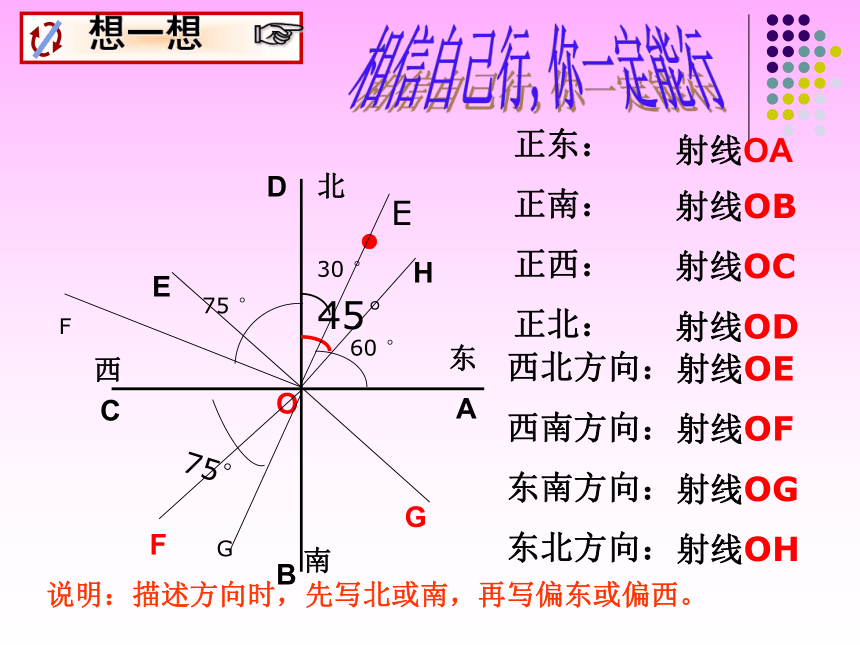
由∠3 与∠4互余 ,可得∠4=90°﹣___。∠1∠3∠1∠3 2、如图,∠AOB=90°,∠COD=∠EOD=90°,C、O、E在一条直线上,试判断∠2与∠3的关系?并试着说明理由? ∠1与∠3呢?321EDBACO4西北南OBCDF东AEH正东:
正南:
正西:
正北:射线OA射线OB
射线OC
射线OD西北方向:
西南方向:
东南方向:
东北方向:射线OE
射线OF
射线OG
射线OHEF相信自己行,你一定能行G说明:描述方向时,先写北或南,再写偏东或偏西。如图,请指出公园、医院、法院各在学校的什么方向?活学活用 加深理解例:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.● A∴射线OA的方向就是南偏东60°,即灯塔A所在的方向。● B● D射线OB的方向就是北偏东40°,即客轮B所在的方向。C ●射线OC的方向就是南偏西10°,即货轮C所在的方向。射线OD的方向就是南偏西45°,即海岛D所在的方向。你有什么收获……
你还有什么困惑?感悟与反思通过这节课的学习:方位角(1) 等角(同角)的补角相等; (2) 等角(同角)的余角相等;课堂小结余角、补角的性质:描述方向时,先写北或南,再写偏东或偏西。如图:西寨中学元月6日将举行运动会,一名服务的同学往返于百米起跑点A、终点B(A、B位于东西方向)及检录处C,他在A处看C点位于北偏东60°的方向上,在B点处看C点位于西北方向上(即北偏西45 ° ),你能确定检录处C的位置么?ABABDEC解:如图所示,过A点作出北偏东60的方向,过B点作出北偏西40的方向,交点就是所求C点的位置(2)检录处C在起点A的北偏东60°的方向上,那么起点A在检录处C的什么方向上呢?A.南偏东30°
B.南偏西30°
C.南偏东60°
D.南偏西60°如果我们在屏幕的O点位置上,你能说出O点的四面八方么?O北南西东东北东南西南西北练一练: 2(1)学生宿舍在校门口的北偏西30°的方向,试画出学生宿舍方向的射线.(2)教学楼在校门口的 方向.北●●●●●●●校门教学楼办公楼综合楼操场学生宿舍餐厅学校平面示意图Next找朋友:图中给出的各角中,哪些互为余角?哪些互为补角?°°°°°°°°在茫茫大海上,我缉私艇正在执行任务,当行驶到某处时,发现有一只可疑船只,这时测得可疑船只在我船的北偏东40°的方向.O北南西东 南偏西25°25° 北偏西70° 南偏东60°射线OA射线OB射线OC70°60°相信自己,你一定行挑战自己!
一个同学站起来说出自己角的度数,与他互为余角或互为补角的同学站起来说出自己的度数,其他同学判断他们做得是否正确。如果正确,给他们鼓掌;如果不正确,大家一起纠正。§4.3.3 余角和补角(2)如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4有什么样的关系?为什么?3答:∠2与∠4相等。
∵ ∠1= ∠3
∴180 °﹣ ∠1= 180 °﹣ ∠3
∴ ∠2 =∠4(等量减等量差相等)
等角的补角相等补角性质提示:1、由∠1与∠2互补,可得∠2=180°﹣____,
2、 由∠3与∠4互补,可得∠4=180°﹣___。
3、 180°﹣ ∠1与180°﹣∠3有什么关系呢?
如图∠1 与∠2互补,∠1 又与∠4互补 ,那么∠2与∠4相等吗?为什么?同角的补角相等补角性质1、如图∠AOB = ∠COD= 180 °,∠AOE= ∠COF,则∠1与∠2是什么关系?试着说明理由。答: ∠1 = ∠2
因为∠AOE= ∠COF
而∠1+ ∠ AOE = 180 °,∠2+ ∠ COF = 180 °
所以∠1 = ∠2(等角的补角相等)AOBCD学以致用? E OF 如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?答:∠2与∠4相等。
∵ ∠1 =∠3
∴ 90°﹣__ =90°﹣__
∴ ∠2 =∠4
等角的余角相等余角的性质分析:由∠1 与∠2互余,可得∠2=90°﹣____,
由∠3 与∠4互余 ,可得∠4=90°﹣___。∠1∠3∠1∠3 2、如图,∠AOB=90°,∠COD=∠EOD=90°,C、O、E在一条直线上,试判断∠2与∠3的关系?并试着说明理由? ∠1与∠3呢?321EDBACO4西北南OBCDF东AEH正东:
正南:
正西:
正北:射线OA射线OB
射线OC
射线OD西北方向:
西南方向:
东南方向:
东北方向:射线OE
射线OF
射线OG
射线OHEF相信自己行,你一定能行G说明:描述方向时,先写北或南,再写偏东或偏西。如图,请指出公园、医院、法院各在学校的什么方向?活学活用 加深理解例:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.● A∴射线OA的方向就是南偏东60°,即灯塔A所在的方向。● B● D射线OB的方向就是北偏东40°,即客轮B所在的方向。C ●射线OC的方向就是南偏西10°,即货轮C所在的方向。射线OD的方向就是南偏西45°,即海岛D所在的方向。你有什么收获……
你还有什么困惑?感悟与反思通过这节课的学习:方位角(1) 等角(同角)的补角相等; (2) 等角(同角)的余角相等;课堂小结余角、补角的性质:描述方向时,先写北或南,再写偏东或偏西。如图:西寨中学元月6日将举行运动会,一名服务的同学往返于百米起跑点A、终点B(A、B位于东西方向)及检录处C,他在A处看C点位于北偏东60°的方向上,在B点处看C点位于西北方向上(即北偏西45 ° ),你能确定检录处C的位置么?ABABDEC解:如图所示,过A点作出北偏东60的方向,过B点作出北偏西40的方向,交点就是所求C点的位置(2)检录处C在起点A的北偏东60°的方向上,那么起点A在检录处C的什么方向上呢?A.南偏东30°
B.南偏西30°
C.南偏东60°
D.南偏西60°如果我们在屏幕的O点位置上,你能说出O点的四面八方么?O北南西东东北东南西南西北练一练: 2(1)学生宿舍在校门口的北偏西30°的方向,试画出学生宿舍方向的射线.(2)教学楼在校门口的 方向.北●●●●●●●校门教学楼办公楼综合楼操场学生宿舍餐厅学校平面示意图Next找朋友:图中给出的各角中,哪些互为余角?哪些互为补角?°°°°°°°°在茫茫大海上,我缉私艇正在执行任务,当行驶到某处时,发现有一只可疑船只,这时测得可疑船只在我船的北偏东40°的方向.O北南西东 南偏西25°25° 北偏西70° 南偏东60°射线OA射线OB射线OC70°60°相信自己,你一定行挑战自己!
