2015年10浙江省普通高中学业水平考试(数学试题)(含答案)
文档属性
| 名称 | 2015年10浙江省普通高中学业水平考试(数学试题)(含答案) | 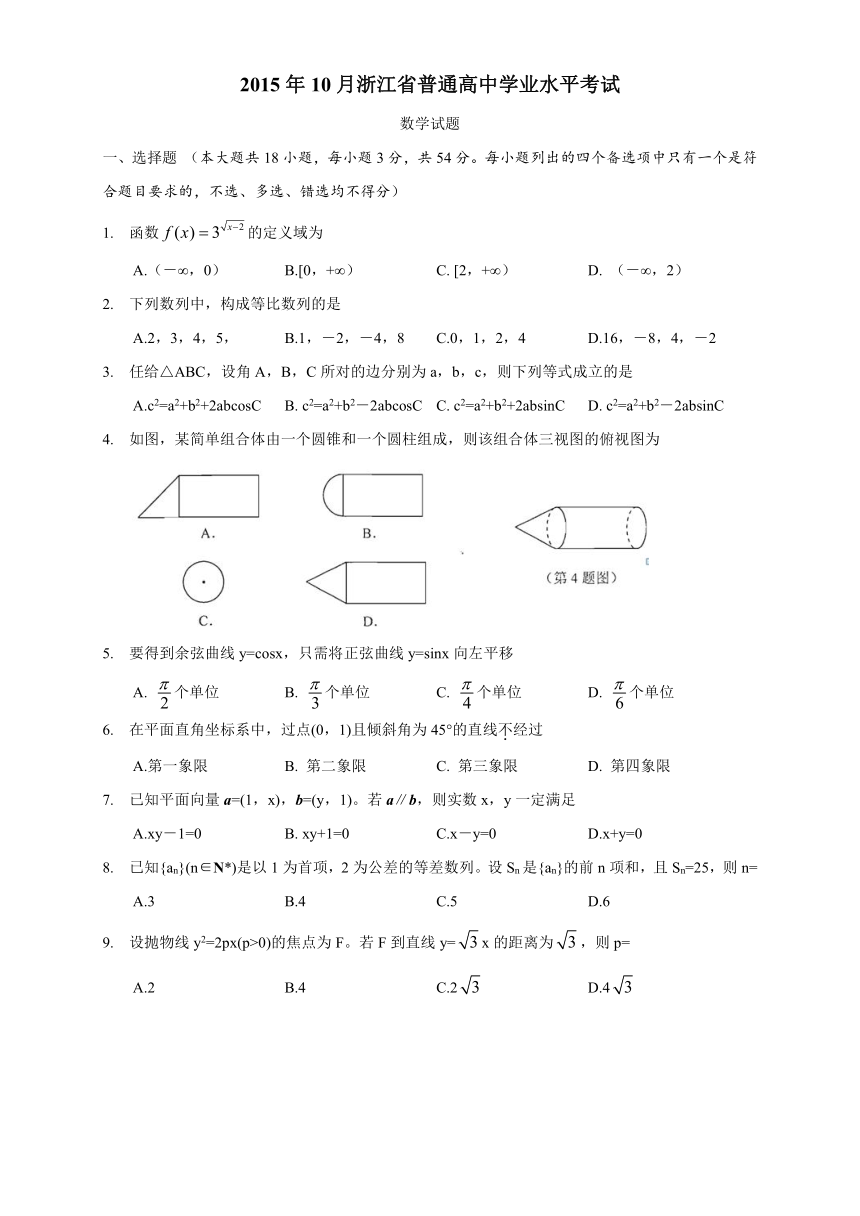 | |
| 格式 | zip | ||
| 文件大小 | 178.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-19 22:08:54 | ||
图片预览


文档简介
2015年10月浙江省普通高中学业水平考试
数学试题
一、选择题 (本大题共18小题,每小题3分,共54分。每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
1. 函数的定义域为
A.(-∞,0) B.[0,+∞) C. [2,+∞) D. (-∞,2)
2. 下列数列中,构成等比数列的是
A.2,3,4,5, B.1,-2,-4,8 C.0,1,2,4 D.16,-8,4,-2
3. 任给△ABC,设角A,B,C所对的边分别为a,b,c,则下列等式成立的是
A.c2=a2+b2+2abcosC B. c2=a2+b2-2abcosC C. c2=a2+b2+2absinC D. c2=a2+b2-2absinC
4. 如图,某简单组合体由一个圆锥和一个圆柱组成,则该组合体三视图的俯视图为
5. 要得到余弦曲线y=cosx,只需将正弦曲线y=sinx向左平移
A. 个单位 B. 个单位 C. 个单位 D. 个单位
6. 在平面直角坐标系中,过点(0,1)且倾斜角为45°的直线不经过
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7. 已知平面向量a=(1,x),b=(y,1)。若a∥b,则实数x,y一定满足
A.xy-1=0 B. xy+1=0 C.x-y=0 D.x+y=0
8. 已知{an}(n∈N*)是以1为首项,2为公差的等差数列。设Sn是{an}的前n项和,且Sn=25,则n=
A.3 B.4 C.5 D.6
9. 设抛物线y2=2px(p>0)的焦点为F。若F到直线y=x的距离为,则p=
A.2 B.4 C.2 D.4
10. 在空间直角坐标系Oxyz中,若y轴上点M到两点P(1,0,2),Q(1,-3,1)的距离相等,则点 M的坐标为
A.(0,1,0) B. (0,-1,0) C. (0,0,3) D. (0,0,-3)
11. 若实数x,y满足 则y的最大值为
A. B.1 C. D.
12. 设a>0,且a≠1,则“a>1”是“loga <1”的
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
13. 如图,在正方体ABCD-A1B1C1D1中,M为棱D1C1的中点。设AM与平面BB1D1D的交点为O, 则
A. 三点D1,O,B共线,且OB=2OD1 B. 三点D1,O,B不共线,且OB=2OD1
C. 三点D1,O,B共线,且OB=OD1 D. 三点D1,O,B不共线,且OB=OD1
(第13题图)
14. 设正实数a,b满足a+λb=2(其中λ为正常数)。若ab的最大值为3,则λ=
A.3 B. C . D.
15. 在空间中,设l,m为两条不同直线,α,β为两个不同的平面,则下列命题正确的是
A.若lα,m不平行于l,则m不平行于α
B.若lα,mβ,且α,β不平行,则l,m不平行
C. 若lα,m不垂直于l,则m不垂直于α
D. 若lα,mβ, l不垂直于m,则α,β不垂直
16. 设a,b,c∈R,下列命题正确的是
A.若|a|<|b|,则|a+c|<|b+c| B. 若|a|<|b|,则|a-c|<|b-c|
C. 若|a|<|b-c|,则|a |<|b|-|c| D. 若|a|<|b-c|,则|a|-|c|<|b|
17. 已知F1,F2分别是双曲线的左、右焦点,l1,l2为双曲线的两条渐近线。设过点M(b,0)且平行于l1的直线交l2于点P。若PF1⊥PF2,则该双曲线的离心率为
A. B. C. D.
(第17题图)
18. 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F。现将△ABD沿对 角线BD翻折,则异面直线BE与CF所成角的取值范围是
A. B. C. D.
(第18题图)
二、填空题(本大题共4小题,每空3分,共15分)
19. 设a,b为平面向量。若a=(1,0),b=(3,4),则|a|= ,a·b=
20. 设全集U={2,3,4},集合A={2,3},则A的补集UA=
21. 在数列{an}(n∈N*)中,设a1=a2=1,a3=2。若数列是等差数列,则a6=
22. 已知函数f(x)=,g(x)=ax+1,其中a>0。若f(x)与g(x)的图象有两个不同的交点, 则a的取值范围是
三、解答题(本大题共3小题,共31分)
23.(本题10分)已知函数f(x)=2sinxcosx,x∈R.
(Ⅰ)求f()的值;
(Ⅱ)求函数f(x)的最小正周期;
(Ⅲ)求函数g(x)=f(x)+f(x+)的最大值。
24. (本题10分)设F1,F2分别是椭圆C:的左、右焦点,过F1且斜率不为零的动直 线l与椭圆C交于A,B两点。
(Ⅰ)求△AF1F2的周长;
(Ⅱ)若存在直线l,使得直线F2A,AB,F2B与直线x=-分别交于P,Q,R三个不同的点,且满足P,Q,R到x轴的距离依次成等比数列,求该直线l的方程。
25. (本题11分)已知函数f(x)=ax,a∈R.
(Ⅰ)判断函数f(x)的奇偶性,并说明理由;
(Ⅱ)当a<2时,证明:函数f(x)在(0,1)上单调递减;
(Ⅲ)若对任意的x∈(0,1)∪(1,+∞),不等式(x-1)[f(x)-]≥0恒成立,求a的取值范围。
数学试题参考答案
一、选择题(本大题共18小题,每小题3分,共54分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D A D A C B B
题号 11 12 13 14 15 16 17 18
答案 B A A D C D B C
二、填空题 (本大题共4小题,每空3分,共15分)
19.1,3 20.{4} 21.120 22.0三、解答题(本大题共3小题,共31分)
23.解: (Ⅰ) 由题意得 f()=2 sincos=1
(Ⅱ) ∵f(x)= sin2x∴函数f(x)的最小正周期为T=π
(Ⅲ) ∵g(x)= sin2x+ sin(2x+)= sin2x+cos2x=
∴当 k∈Z时,函数g(x)的最大值为
24.解: (Ⅰ)因为椭圆的长轴长2a=2 ,焦距2c=2.
又由椭圆的定义得 |AF1|+|AF2|=2a
所以△AF1F2的周长为|AF1|+|AF2|+|F1F2|=2+2
(Ⅱ)由题意得l不垂直两坐标轴,故设l的方程为y=k(x+1)(k≠0)
于是直线l与直线x=-交点Q的纵坐标为
设 A(x1,y1),B(x2,y2),显然x1,x2≠1,
所以直线F2A的方程为
故直线F2A与直线x=-交点P的纵坐标为
同理,点R的纵坐标为
因为P,Q,R到x轴的距离依次成等比数列,所以|yP|·|yR|=|yQ|2
即
即
整理得。(*)
联立 消去y得(1+2k2)x2+4k2x+2k2-2=0
所以x1+x2= ,x1x2=
代入(*)得
化简得|8k2-1|=9
解得k=
经检验,直线l的方程为y=(x+1)
25. (Ⅰ)解:因为f(-x)=-ax=-( ax)=-f(x)
又因为f(x)的定义域为{x∈R|x≠-1且x≠1}
所以函数f(x)为奇函数。
(Ⅱ)证明:任取x1,x2∈(0,1),设x1f(x1)-f(x2)=a(x1-x2)+
=
=
因为02,0<(x12-1)(x22-1)<1
所以
所以
又因为x1-x2<0,所以f(x1)>f(x2)
所以函数f(x)在(0,1)上单调递减
(Ⅲ)解:因为(x-1)[f(x)-]=(x-1)[ ax-]
==
所以不等式ax2(x2-1)+2≥0对任意的x∈(0,1)∪(1,+∞)恒成立。
令函数g(t)=at2-at+2,其中t=x2,t>0且t≠1.
①当a<0时,抛物线y=g(t)开口向下,不合题意;
②当a=0时,g(t)=2>0恒成立,所以a=0符合题意;
③当a>0时,因为g(t)=a(t-)2-+2
所以只需-+2≥0
即0综上,a的取值范围是0≤a≤8
数学试题
一、选择题 (本大题共18小题,每小题3分,共54分。每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
1. 函数的定义域为
A.(-∞,0) B.[0,+∞) C. [2,+∞) D. (-∞,2)
2. 下列数列中,构成等比数列的是
A.2,3,4,5, B.1,-2,-4,8 C.0,1,2,4 D.16,-8,4,-2
3. 任给△ABC,设角A,B,C所对的边分别为a,b,c,则下列等式成立的是
A.c2=a2+b2+2abcosC B. c2=a2+b2-2abcosC C. c2=a2+b2+2absinC D. c2=a2+b2-2absinC
4. 如图,某简单组合体由一个圆锥和一个圆柱组成,则该组合体三视图的俯视图为
5. 要得到余弦曲线y=cosx,只需将正弦曲线y=sinx向左平移
A. 个单位 B. 个单位 C. 个单位 D. 个单位
6. 在平面直角坐标系中,过点(0,1)且倾斜角为45°的直线不经过
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7. 已知平面向量a=(1,x),b=(y,1)。若a∥b,则实数x,y一定满足
A.xy-1=0 B. xy+1=0 C.x-y=0 D.x+y=0
8. 已知{an}(n∈N*)是以1为首项,2为公差的等差数列。设Sn是{an}的前n项和,且Sn=25,则n=
A.3 B.4 C.5 D.6
9. 设抛物线y2=2px(p>0)的焦点为F。若F到直线y=x的距离为,则p=
A.2 B.4 C.2 D.4
10. 在空间直角坐标系Oxyz中,若y轴上点M到两点P(1,0,2),Q(1,-3,1)的距离相等,则点 M的坐标为
A.(0,1,0) B. (0,-1,0) C. (0,0,3) D. (0,0,-3)
11. 若实数x,y满足 则y的最大值为
A. B.1 C. D.
12. 设a>0,且a≠1,则“a>1”是“loga <1”的
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
13. 如图,在正方体ABCD-A1B1C1D1中,M为棱D1C1的中点。设AM与平面BB1D1D的交点为O, 则
A. 三点D1,O,B共线,且OB=2OD1 B. 三点D1,O,B不共线,且OB=2OD1
C. 三点D1,O,B共线,且OB=OD1 D. 三点D1,O,B不共线,且OB=OD1
(第13题图)
14. 设正实数a,b满足a+λb=2(其中λ为正常数)。若ab的最大值为3,则λ=
A.3 B. C . D.
15. 在空间中,设l,m为两条不同直线,α,β为两个不同的平面,则下列命题正确的是
A.若lα,m不平行于l,则m不平行于α
B.若lα,mβ,且α,β不平行,则l,m不平行
C. 若lα,m不垂直于l,则m不垂直于α
D. 若lα,mβ, l不垂直于m,则α,β不垂直
16. 设a,b,c∈R,下列命题正确的是
A.若|a|<|b|,则|a+c|<|b+c| B. 若|a|<|b|,则|a-c|<|b-c|
C. 若|a|<|b-c|,则|a |<|b|-|c| D. 若|a|<|b-c|,则|a|-|c|<|b|
17. 已知F1,F2分别是双曲线的左、右焦点,l1,l2为双曲线的两条渐近线。设过点M(b,0)且平行于l1的直线交l2于点P。若PF1⊥PF2,则该双曲线的离心率为
A. B. C. D.
(第17题图)
18. 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F。现将△ABD沿对 角线BD翻折,则异面直线BE与CF所成角的取值范围是
A. B. C. D.
(第18题图)
二、填空题(本大题共4小题,每空3分,共15分)
19. 设a,b为平面向量。若a=(1,0),b=(3,4),则|a|= ,a·b=
20. 设全集U={2,3,4},集合A={2,3},则A的补集UA=
21. 在数列{an}(n∈N*)中,设a1=a2=1,a3=2。若数列是等差数列,则a6=
22. 已知函数f(x)=,g(x)=ax+1,其中a>0。若f(x)与g(x)的图象有两个不同的交点, 则a的取值范围是
三、解答题(本大题共3小题,共31分)
23.(本题10分)已知函数f(x)=2sinxcosx,x∈R.
(Ⅰ)求f()的值;
(Ⅱ)求函数f(x)的最小正周期;
(Ⅲ)求函数g(x)=f(x)+f(x+)的最大值。
24. (本题10分)设F1,F2分别是椭圆C:的左、右焦点,过F1且斜率不为零的动直 线l与椭圆C交于A,B两点。
(Ⅰ)求△AF1F2的周长;
(Ⅱ)若存在直线l,使得直线F2A,AB,F2B与直线x=-分别交于P,Q,R三个不同的点,且满足P,Q,R到x轴的距离依次成等比数列,求该直线l的方程。
25. (本题11分)已知函数f(x)=ax,a∈R.
(Ⅰ)判断函数f(x)的奇偶性,并说明理由;
(Ⅱ)当a<2时,证明:函数f(x)在(0,1)上单调递减;
(Ⅲ)若对任意的x∈(0,1)∪(1,+∞),不等式(x-1)[f(x)-]≥0恒成立,求a的取值范围。
数学试题参考答案
一、选择题(本大题共18小题,每小题3分,共54分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D A D A C B B
题号 11 12 13 14 15 16 17 18
答案 B A A D C D B C
二、填空题 (本大题共4小题,每空3分,共15分)
19.1,3 20.{4} 21.120 22.0
23.解: (Ⅰ) 由题意得 f()=2 sincos=1
(Ⅱ) ∵f(x)= sin2x∴函数f(x)的最小正周期为T=π
(Ⅲ) ∵g(x)= sin2x+ sin(2x+)= sin2x+cos2x=
∴当 k∈Z时,函数g(x)的最大值为
24.解: (Ⅰ)因为椭圆的长轴长2a=2 ,焦距2c=2.
又由椭圆的定义得 |AF1|+|AF2|=2a
所以△AF1F2的周长为|AF1|+|AF2|+|F1F2|=2+2
(Ⅱ)由题意得l不垂直两坐标轴,故设l的方程为y=k(x+1)(k≠0)
于是直线l与直线x=-交点Q的纵坐标为
设 A(x1,y1),B(x2,y2),显然x1,x2≠1,
所以直线F2A的方程为
故直线F2A与直线x=-交点P的纵坐标为
同理,点R的纵坐标为
因为P,Q,R到x轴的距离依次成等比数列,所以|yP|·|yR|=|yQ|2
即
即
整理得。(*)
联立 消去y得(1+2k2)x2+4k2x+2k2-2=0
所以x1+x2= ,x1x2=
代入(*)得
化简得|8k2-1|=9
解得k=
经检验,直线l的方程为y=(x+1)
25. (Ⅰ)解:因为f(-x)=-ax=-( ax)=-f(x)
又因为f(x)的定义域为{x∈R|x≠-1且x≠1}
所以函数f(x)为奇函数。
(Ⅱ)证明:任取x1,x2∈(0,1),设x1
=
=
因为0
所以
所以
又因为x1-x2<0,所以f(x1)>f(x2)
所以函数f(x)在(0,1)上单调递减
(Ⅲ)解:因为(x-1)[f(x)-]=(x-1)[ ax-]
==
所以不等式ax2(x2-1)+2≥0对任意的x∈(0,1)∪(1,+∞)恒成立。
令函数g(t)=at2-at+2,其中t=x2,t>0且t≠1.
①当a<0时,抛物线y=g(t)开口向下,不合题意;
②当a=0时,g(t)=2>0恒成立,所以a=0符合题意;
③当a>0时,因为g(t)=a(t-)2-+2
所以只需-+2≥0
即0
同课章节目录
