2025年九年级下学期数学模拟考试试题以及答案(适用北师大版)(word版,含答案)
文档属性
| 名称 | 2025年九年级下学期数学模拟考试试题以及答案(适用北师大版)(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 571.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 08:55:59 | ||
图片预览



文档简介
2025年九年级学业水平数学模拟考试试题
(考试时间120分钟 满分150分)
一、选择题:本题共10小题,每小题4分,共40分.每小题只有一个选项符合题目要求.
1.的绝对值是( )
A .-2025 B . C. D .﹣
2.据中国物流与采购联合会消息,2024年前三季度我国冷链物流总额为64000亿元,同比增长4.2%.将数据"64000"用科学记数法表示为( )
A .0.64x106 B .6.4x105 C .6.4x104 D .64x105
3.2024年7月26日至8月11日在法国巴黎举行第33届夏季奥运会,下列四幅巴黎奥运会项目图标中,是轴对称图形的是( )
4.下列运算正确的是( )
A .5m+ n =5mn B .5m-2m=3 C .3n2+2n3=5n5 D .-m2n+2m2n=m2n
如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=53°,则∠2的度数为( )
A .53° B .47° C .37° D .27°
6.如图,数轴上的A , B 两点分别表示有理数a , b ,下列式子中,不正确的是( )
A . a + b <0 B . a - b <0 C .- a + b >0 D .- b >- a
7.北京时间12月4日,我国申报的"春节﹣﹣中国人庆祝传统新年的社会实践"通过评审,列入联合国教科文组织人类非物质文化遗产代表作名录.现将四张大小相同的正方形卡片拼成如图所示的正方形靶盘(其中两张卡片上是"春"字,另外两张上是"福"字).现向该靶盘随机掷两次飞镖,则两次射中的卡片上的字不相同的概率为( )
A. B. C. D.
8.已知函数 y=中,在每个象限内,y 随 x 的增大而增大,那么它和函数y = kx 在同一直角坐标平面内的大致图象是( )
9.如图,在口ABCD 中,AB =6, AD =9,以点A 为圆心,AB长为半径画弧交AD 于点F ;以点A 为
圆心,适当长为半径画弧分别交AB,AD于M,N两点。分别以点M,N为圆心,大于MN的长为半径画弧,两弧在平行四边形内交于点G ,连接AG 并延长交BC 于点 E ,连接EF , BD , BD 分别交AE , EF 于P , Q 两点,下列结论不正确的是( )
A . AE 平分∠BAD B .四边形 ABEF 是菱形 C.= D . PQ = QD
10.对于二次函数 y =ax2+ bx + c ,规定函数y=是它的相关函数.已知点M , N的坐标分别为(﹣,1),(,1)。连接 MN ,若线段 MN 与二次函数 y =-x2+4x+ n 的相关函数的图象有两个公共点,则 n 的取值范围为( )
A.﹣3<n≤﹣1或1<n≤ B .﹣3<n<﹣1或1≤n≤
C . n ≤-1或1< n ≤ D .-3< n <-1或 n ≥1
二、填空题:本题共5小题,每小题4分,共20分.直接填写答案.
11.分解因式:3ay2-3ax2= 。
12.在一个不透明的口袋中装有3个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 个.
13.已知关于 x 的一元二次方程x2+3x- c =0的两根为2和m ,则m +2的值为 .
14.某市去年居民用水按照4.6元/吨收取费用,为提倡居民节约用水,自今年1月1日起对居民用水实行阶梯水费,规定:若用水超过 a 吨,超过 a 吨的部分每吨增加2元.图中4,12分别表示去年、今年水费 y (元)与用水量 x (吨)之间的关系.实行阶梯水费后,若用水超过 a 吨,则超过 a 吨的部分每吨水费为 元.
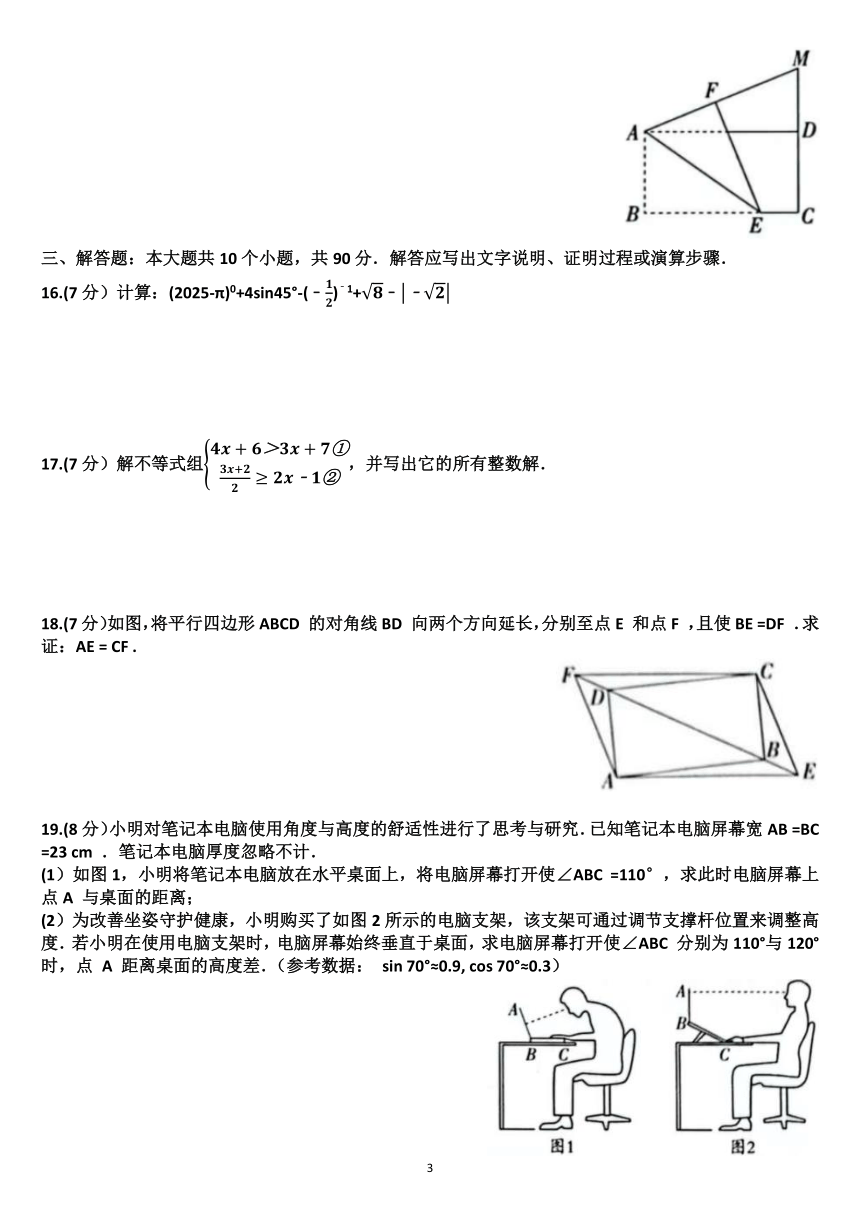
15.如图,在矩形ABCD 中,AB =4, BC =8,点E 是射线 BC 上一点,=3,连接 AE ,将△ABE 沿
AE 翻折,得到△AFE ,延长 AF 交 CD 的延长线于点M ,则DM = .
解答题:本大题共10个小题,共90分.解答应写出文字说明、证明过程或演算步骤.
16.(7分)计算:(2025-π)0+4sin45°-(﹣)﹣1+﹣
17.(7分)解不等式组,并写出它的所有整数解.
18.(7分)如图,将平行四边形ABCD 的对角线BD 向两个方向延长,分别至点E 和点F ,且使BE =DF .求证:AE = CF .
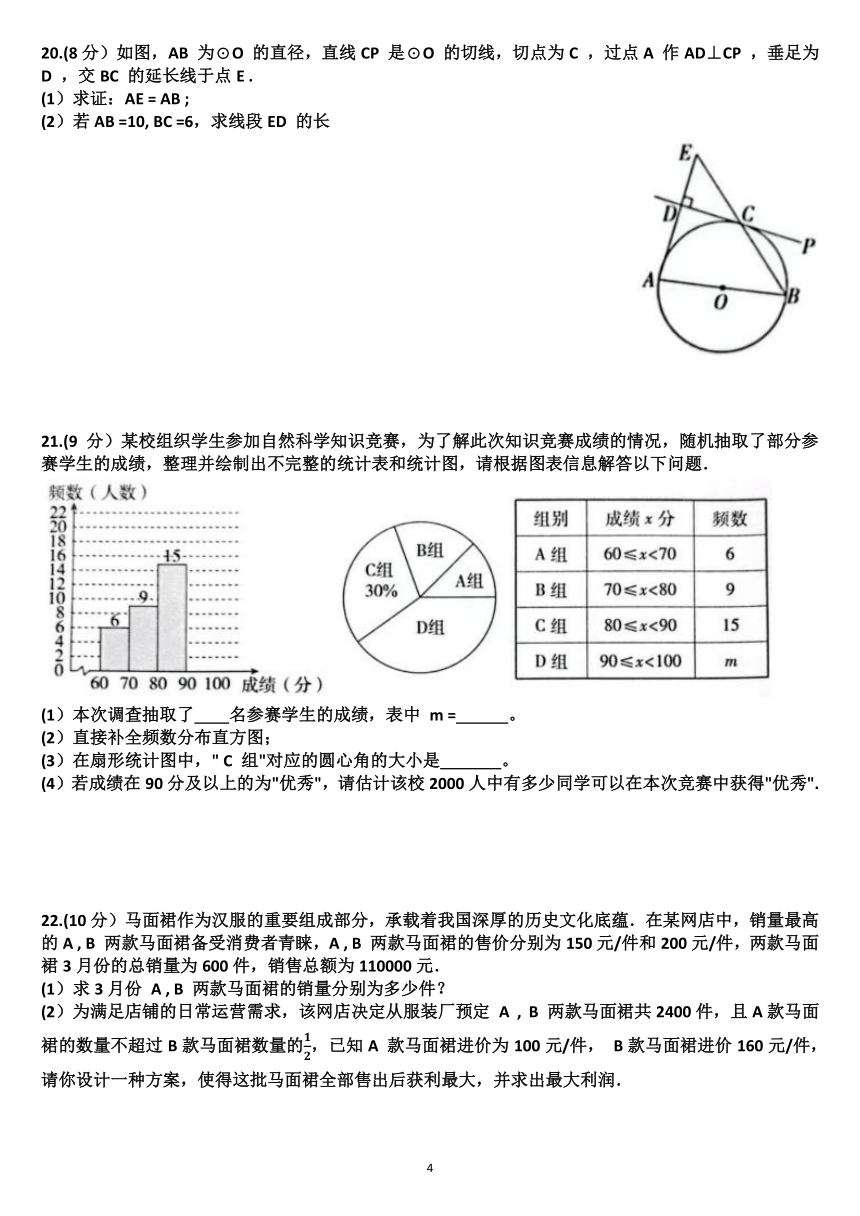
19.(8分)小明对笔记本电脑使用角度与高度的舒适性进行了思考与研究.已知笔记本电脑屏幕宽AB =BC =23 cm .笔记本电脑厚度忽略不计.
(1)如图1,小明将笔记本电脑放在水平桌面上,将电脑屏幕打开使∠ABC =110°,求此时电脑屏幕上点A 与桌面的距离;
(2)为改善坐姿守护健康,小明购买了如图2所示的电脑支架,该支架可通过调节支撑杆位置来调整高度.若小明在使用电脑支架时,电脑屏幕始终垂直于桌面,求电脑屏幕打开使∠ABC 分别为110°与120°时,点 A 距离桌面的高度差.(参考数据: sin 70°≈0.9, cos 70°≈0.3)
20.(8分)如图,AB 为⊙O 的直径,直线CP 是⊙O 的切线,切点为C ,过点A 作AD⊥CP ,垂足为D ,交BC 的延长线于点E .
(1)求证:AE = AB ;
(2)若AB =10, BC =6,求线段ED 的长
21.(9分)某校组织学生参加自然科学知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出不完整的统计表和统计图,请根据图表信息解答以下问题.
(1)本次调查抽取了 名参赛学生的成绩,表中 m = 。
(2)直接补全频数分布直方图;
(3)在扇形统计图中," C 组"对应的圆心角的大小是 。
(4)若成绩在90分及以上的为"优秀",请估计该校2000人中有多少同学可以在本次竞赛中获得"优秀".
22.(10分)马面裙作为汉服的重要组成部分,承载着我国深厚的历史文化底蕴.在某网店中,销量最高的A , B 两款马面裙备受消费者青睐,A , B 两款马面裙的售价分别为150元/件和200元/件,两款马面裙3月份的总销量为600件,销售总额为110000元.
(1)求3月份 A , B 两款马面裙的销量分别为多少件?
(2)为满足店铺的日常运营需求,该网店决定从服装厂预定 A , B 两款马面裙共2400件,且A款马面裙的数量不超过B款马面裙数量的,已知A 款马面裙进价为100元/件, B款马面裙进价160元/件,请你设计一种方案,使得这批马面裙全部售出后获利最大,并求出最大利润.
23.(10分)如图,在平面直角坐标系x0y中,直线 y =2x+6与反比例函数 y =的图象交于 A (-1, m ),B 两点,C 为反比例函数图象第四象限上的一点。
(1)求反比例函数的表达式及点 B 的坐标;
(2)当△AOB 与△AOC 的面积相等时,求此时点C 的坐标;
(3)我们把对角线互相垂直且相等的四边形称为"垂等四边形",设点D 是平面内一点,是否存在这样的C , D 两点,使四边形ABCD 是"垂等四边形",且该四边形的两条对角线相交于点Q ,△ABQ ~△ACB ?若存在,求出C , D两点的坐标;若不存在,请说明理由.
24.(12分)如图1,抛物线 y =x2+bx与 x 轴交于点A ,与直线OB 交于点 B (6,6),过点A 作直线OB 的平行线,交抛物线于点 C .
(1)求抛物线 y =x2+ bx 的表达式;
(2)点D 为直线AC 下方抛物线上一点,过点 D作 DE⊥x 轴交直线OB 于点E ,过点E 作 EF⊥AC 于点F ,连接DF .求△DEF 面积的最大值,及此时点D 的坐标;
(3)如图2,在(2)问条件下,将原抛物线向右平移,再次经过(2)问条件下的点D 时,新抛物线与x 轴交于点M , N (M 在N 左侧),与y 轴交于点G ,点P 为新抛物线上的一点,连接DP ,并延长DP 交直线GN 于点H ,使得∠DHN =2∠DGN,写出所有符合条件的点H 的坐标,并写出求解点H 的坐标的其中一种情况的过程.
25.(12分)全等三角形是我们初中数学的重要知识点之一,它为我们学习后面几何知识做好铺垫,掌握全等三角形的证明是做一系列复杂几何证明的基础。
【问题初探】
(1)构造全等三角形的方法有很多,有一种常见的方法是作高线,将需要证明的边或角放在两个直角三角形中进而通过全等证明关系.比如,我们可以通过作高线证明三角形中一个重要的结论"在同一个三角形中,如果两个角相等,那么这两个角所对的边也相等".现在请你完成小聪同学的证明过程;如图1,在△ ABC 中,已知∠B =∠C ,可证 AB = AC ,小聪同学的作法是作 BC 边上的高线 AD .
【类比分析】
(2)通过上述例子,我们发现通过作高线构造直角三角形证明全等确实是一种有效的方法,由此推出了三角形中的重要结论.现在请你借助上述的方法或结论继续探索,如图2,在△ ABC 中,已知∠ABC = ∠ACB ,点E 为边AC 上一点,点F 为边AB 延长线上一点,连接EF 说明理由;与边BC 交于点D ,若点D 恰为线段EF 的中点,试探究线段CE 与线段BF 的数量关系,并说明理由.
【学以致用】
(3)如图3,在△ABC 中,∠CAB =90°, AD , AE 分别为△ABC 的角平分线和中线,过点E 作EF⊥AD 与线段AD 的延长线交于点G ,与边AB 的延长线交于点F ,已知△ABC 的面积是30,线段 AF 的长为8,求△ AED 的面积.
答案
一、选择题:本题共10小题,每小题4分,共40分.每小题只有一个选项符合题目要求.
1.的绝对值是( B )
A .-2025 B . C. D .﹣
2.据中国物流与采购联合会消息,2024年前三季度我国冷链物流总额为64000亿元,同比增长4.2%.将数据"64000"用科学记数法表示为( C )
A .0.64x106 B .6.4x105 C .6.4x104 D .64x105
3.2024年7月26日至8月11日在法国巴黎举行第33届夏季奥运会,下列四幅巴黎奥运会项目图标中,是轴对称图形的是( B )
4.下列运算正确的是( D )
A .5m+ n =5mn B .5m-2m=3 C .3n2+2n3=5n5 D .-m2n+2m2n=m2n
如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=53°,则∠2的度数为( C )
A .53° B .47° C .37° D .27°
6.如图,数轴上的A , B 两点分别表示有理数a , b ,下列式子中,不正确的是( D )
A . a + b <0 B . a - b <0 C .- a + b >0 D .- b >- a
7.北京时间12月4日,我国申报的"春节﹣﹣中国人庆祝传统新年的社会实践"通过评审,列入联合国教科文组织人类非物质文化遗产代表作名录.现将四张大小相同的正方形卡片拼成如图所示的正方形靶盘(其中两张卡片上是"春"字,另外两张上是"福"字).现向该靶盘随机掷两次飞镖,则两次射中的卡片上的字不相同的概率为( A )
A. B. C. D.
8.已知函数 y=中,在每个象限内,y 随 x 的增大而增大,那么它和函数y = kx 在同一直角坐标平面内的大致图象是( B )
9.如图,在口ABCD 中,AB =6, AD =9,以点A 为圆心,AB长为半径画弧交AD 于点F ;以点A 为
圆心,适当长为半径画弧分别交AB,AD于M,N两点。分别以点M,N为圆心,大于MN的长为半径画弧,两弧在平行四边形内交于点G ,连接AG 并延长交BC 于点 E ,连接EF , BD , BD 分别交AE , EF 于P , Q 两点,下列结论不正确的是( D )
A . AE 平分∠BAD B .四边形 ABEF 是菱形 C.= D . PQ = QD
10.对于二次函数 y =ax2+ bx + c ,规定函数y=是它的相关函数.已知点M , N的坐标分别为(﹣,1),(,1)。连接 MN ,若线段 MN 与二次函数 y =-x2+4x+ n 的相关函数的图象有两个公共点,则 n 的取值范围为( A )
A.﹣3<n≤﹣1或1<n≤ B .﹣3<n<﹣1或1≤n≤
C . n ≤-1或1< n ≤ D .-3< n <-1或 n ≥1
二、填空题:本题共5小题,每小题4分,共20分.直接填写答案.
11.分解因式:3ay2-3ax2= 3a(y﹣x)(y+x) 。
12.在一个不透明的口袋中装有3个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 9 个.
13.已知关于 x 的一元二次方程x2+3x- c =0的两根为2和m ,则m +2的值为 ﹣3 .
14.某市去年居民用水按照4.6元/吨收取费用,为提倡居民节约用水,自今年1月1日起对居民用水实行阶梯水费,规定:若用水超过 a 吨,超过 a 吨的部分每吨增加2元.图中4,12分别表示去年、今年水费 y (元)与用水量 x (吨)之间的关系.实行阶梯水费后,若用水超过 a 吨,则超过 a 吨的部分每吨水费为 5.5 元.
15.如图,在矩形ABCD 中,AB =4, BC =8,点E 是射线 BC 上一点,=3,连接 AE ,将△ABE 沿
AE 翻折,得到△AFE ,延长 AF 交 CD 的延长线于点M ,则DM = 或 .
解答题:本大题共10个小题,共90分.解答应写出文字说明、证明过程或演算步骤.
16.(7分)计算:(2025-π)0+4sin45°-(﹣)﹣1+﹣
=1+2+2+2﹣
=3+3
17.(7分)解不等式组,并写出它的所有整数解.
解:由①,得 x >1
由②,得 x ≤4.
所以不等式组的解集为1< x≤4.
所以整数解为2,3,4.
18.(7分)如图,将平行四边形ABCD 的对角线BD 向两个方向延长,分别至点E 和点F ,且使BE =DF .求证:AE = CF .
证明:∵四边形ABCD 为平行四边形,
∴CD = AB , CD∥AB
∴∠ABD = ∠CDB .
∵∠ABD =180°- ∠ABE ,∠CDB =180°- ∠CDF
∴∠ABE = ∠CDF .
在△ ABE 和△ CDF 中
△ABE≌△CDF ( SAS )
∴AE = CF .
19.(8分)小明对笔记本电脑使用角度与高度的舒适性进行了思考与研究.已知笔记本电脑屏幕宽AB =BC =23 cm .笔记本电脑厚度忽略不计.
(1)如图1,小明将笔记本电脑放在水平桌面上,将电脑屏幕打开使∠ABC =110°,求此时电脑屏幕上点A 与桌面的距离;
(2)为改善坐姿守护健康,小明购买了如图2所示的电脑支架,该支架可通过调节支撑杆位置来调整高度.若小明在使用电脑支架时,电脑屏幕始终垂直于桌面,求电脑屏幕打开使∠ABC 分别为110°与120°时,点 A 距离桌面的高度差.(参考数据: sin 70°≈0.9, cos 70°≈0.3)
解:(1)如图1,过点 A作 AD⊥BC ,垂足为 D
∵∠ABC =110°
∴∠ABD =180°-∠ABC =70°.
在 Rt△ABD 中,AB =23 cm
∴AD = AB·sin∠ABD =23xsin70°≈23x0.9=20.7( cm )
∴此时电脑屏幕上点 A 与桌面的距离约为20.7 cm .
如图2,延长AB 交CE 于点 F ,由题意,得BF⊥CE
∴∠BFC =90°.
当∠ABC =120时, ∠CBF =180°-∠ABC =60°
在Rt△BCF 中,BC =23 cm
∴BF = BC·cos 60°=23x=11.5( cm ).
当∠ABC =110°时,∠CBF =180°- ∠ABC =70°
在Rt△BCF 中, BC=23 cm
∴BF = BC·cos 70°≈23x0.3=6.9( cm ),11.5-6.9=4.6( cm ).
∴点 A 距离桌面的高度差约为4.6 cm .
20.(8分)如图,AB 为⊙O 的直径,直线CP 是⊙O 的切线,切点为C ,过点A 作AD⊥CP ,垂足为D ,交BC 的延长线于点E .
(1)求证:AE = AB ;
(2)若AB =10, BC =6,求线段ED 的长
(1)证明:如图,连接OC ,则OC = OB
∴∠B =∠OCB
∵CP 与⊙O 相切于点C
∴CP⊥OC.
∵AD⊥CP
∴AD // OC .
∴∠E = ∠OCB .
∴∠B = ∠E .
∴AE = AB .
(2)解:如图,连接 AC ,AB 为⊙O 的直径,
∴∠ACE = ∠ACB =90°.
∵AE = AB =10, AC⊥BE
∴EC = BC =6.
∵∠CDE = ∠ACE =90°, ∠E = ∠E
∴△CDE∽△ACE .
∴==
∴ED=
21.(9分)某校组织学生参加自然科学知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出不完整的统计表和统计图,请根据图表信息解答以下问题.
(1)本次调查抽取了 名参赛学生的成绩,表中 m = 。
(2)直接补全频数分布直方图;
(3)在扇形统计图中," C 组"对应的圆心角的大小是 。
(4)若成绩在90分及以上的为"优秀",请估计该校2000人中有多少同学可以在本次竞赛中获得"优秀".
解:(1)样本容量为15÷30%=50 m =50-6-9-15=20.
(2)补全频数分布直方图如下:
(3)" C 组"对应的圆心角的大小是360°x30%=108°.
(4)2000x=800(人).
答:估计该校2000人中有800名同学可以在本次竞
22.(10分)马面裙作为汉服的重要组成部分,承载着我国深厚的历史文化底蕴.在某网店中,销量最高的A , B 两款马面裙备受消费者青睐,A , B 两款马面裙的售价分别为150元/件和200元/件,两款马面裙3月份的总销量为600件,销售总额为110000元.
(1)求3月份 A , B 两款马面裙的销量分别为多少件?
(2)为满足店铺的日常运营需求,该网店决定从服装厂预定 A , B 两款马面裙共2400件,且A款马面裙的数量不超过B款马面裙数量的,已知A 款马面裙进价为100元/件, B款马面裙进价160元/件,请你设计一种方案,使得这批马面裙全部售出后获利最大,并求出最大利润.
解:(1)设3月份A 款马面裙的销量为x 件,B 款马面裙的销量为y 件
由题意,得,解得
答:3月份 A 款马面裙的销量为200件, B 款马面裙的销量为400件.
(2)设网店购进 A 款马面裙 a 件,再购进 B 款马面裙(2400- a )件,总利润为 w 元,
a≤(2400- a ),解得 a≤800
由题意,得 w =(150-100) a +(200-160)(2400- a )=10a+96000,
∵10>0
∴w 随 a 的增大而增大.
当 a =800时,w 取最大值,
w的最大值=10x800+96000=104000.
此时2400- x =2400-800=1600.
答:网店购进 A 款马面裙800件, B 款马面裙1600件,获利最大,最大利润为104000元.
23.(10分)如图,在平面直角坐标系x0y中,直线 y =2x+6与反比例函数 y =的图象交于 A (-1, m ),B 两点,C 为反比例函数图象第四象限上的一点。
(1)求反比例函数的表达式及点 B 的坐标;
(2)当△AOB 与△AOC 的面积相等时,求此时点C 的坐标;
(3)我们把对角线互相垂直且相等的四边形称为"垂等四边形",设点D 是平面内一点,是否存在这样的C , D 两点,使四边形ABCD 是"垂等四边形",且该四边形的两条对角线相交于点Q ,△ABQ ~△ACB ?若存在,求出C , D两点的坐标;若不存在,请说明理由.
解:(1)当x =-1时, y =2x+6=4,即点 A (-1,4),将点 A 的坐标代人反比例函数的表达式,得 k=-1x4=-4
即反比例函数的表达式为 y =﹣
联立两个函数表达式,得﹣=2x+6
解得x =-1或﹣2,即B (-2,2).
(2)由A , B 的坐标,得 S△AOB =3,设 C ( n ,﹣)
由点A , C 的坐标,得直线AC 的函数表达式为 y =﹣(x+1)+4
设直线 AC 交 y 轴于点H (0,4-)
则△AOC 的面积= ×(n+1)=3
解得 n =2或
C1(2,-2), C2 (,-8).
(3)C(4,﹣1) D(3,7)
24.(12分)如图1,抛物线 y =x2+bx与 x 轴交于点A ,与直线OB 交于点 B (6,6),过点A 作直线OB 的平行线,交抛物线于点 C .
(1)求抛物线 y =x2+ bx 的表达式;
(2)点D 为直线AC 下方抛物线上一点,过点 D作 DE⊥x 轴交直线OB 于点E ,过点E 作 EF⊥AC 于点F ,连接DF .求△DEF 面积的最大值,及此时点D 的坐标;
(3)如图2,在(2)问条件下,将原抛物线向右平移,再次经过(2)问条件下的点D 时,新抛物线与x 轴交于点M , N (M 在N 左侧),与y 轴交于点G ,点P 为新抛物线上的一点,连接DP ,并延长DP 交直线GN 于点H ,使得∠DHN =2∠DGN,写出所有符合条件的点H 的坐标,并写出求解点H 的坐标的其中一种情况的过程.
解:(1)将点 B 的坐标代人函数表达式,得6=36+6b,解得 b =-5.
∴抛物线的表达式为 y =x2-5x.
(2)由抛物线的表达式,得点 A (5,0),由点 B 的坐标,得直线OB 的表达式为y = x
∵FC // OB且直线 FC 过点 A
∴直线 FC 的表达式为 y = x -5.
设点E ( m , m ),则点D ( m ,m2-5m), Q ( m , m -5).
∴DE =-m2+6m, EQ =5.
如图1,过点 F 作 FW⊥ED 于点 W ,EF⊥OB , OB 和水平线的夹角为45°,
∴△EFW为等腰直角三角形.
同理可得△FWQ 为等腰直角三角形,
∴FW =EQ=
∴△DEF面积=﹣(m﹣3)2+
即△ DEF 面积的最大值为,此时m =3,点 D 的坐标为(3,-6).
(3)H(,)或(,﹣)
25.(12分)全等三角形是我们初中数学的重要知识点之一,它为我们学习后面几何知识做好铺垫,掌握全等三角形的证明是做一系列复杂几何证明的基础。
【问题初探】
(1)构造全等三角形的方法有很多,有一种常见的方法是作高线,将需要证明的边或角放在两个直角三角形中进而通过全等证明关系.比如,我们可以通过作高线证明三角形中一个重要的结论"在同一个三角形中,如果两个角相等,那么这两个角所对的边也相等".现在请你完成小聪同学的证明过程;如图1,在△ ABC 中,已知∠B =∠C ,可证 AB = AC ,小聪同学的作法是作 BC 边上的高线 AD .
【类比分析】
(2)通过上述例子,我们发现通过作高线构造直角三角形证明全等确实是一种有效的方法,由此推出了三角形中的重要结论.现在请你借助上述的方法或结论继续探索,如图2,在△ ABC 中,已知∠ABC = ∠ACB ,点E 为边AC 上一点,点F 为边AB 延长线上一点,连接EF 说明理由;与边BC 交于点D ,若点D 恰为线段EF 的中点,试探究线段CE 与线段BF 的数量关系,并说明理由.
【学以致用】
(3)如图3,在△ABC 中,∠CAB =90°, AD , AE 分别为△ABC 的角平分线和中线,过点E 作EF⊥AD 与线段AD 的延长线交于点G ,与边AB 的延长线交于点F ,已知△ABC 的面积是30,线段 AF 的长为8,求△ AED 的面积.
(1)证明:∵AD 是△ ABC 的高线,
∴∠ADB = ∠ADC =90°.
∵AD = AD , ∠B = ∠C
∴△ADB≌△ADC ( AAS ).
∴AB = AC .
(2)解: CE = BF ,
理由:过点 E 作 EG∥AB 交 BC 于点 G ,
∴∠F=∠DEG,∠FBD=∠EGD
∵点 D 恰为线段 EF 的中点
∴DF = DE
∴△BFD≌ GED ( AAS )
∴BF = EG
∵∠ABC =∠ACB
∴∠BGC =∠ECG
∴EG = CE
∴CE = BF
(3)
(考试时间120分钟 满分150分)
一、选择题:本题共10小题,每小题4分,共40分.每小题只有一个选项符合题目要求.
1.的绝对值是( )
A .-2025 B . C. D .﹣
2.据中国物流与采购联合会消息,2024年前三季度我国冷链物流总额为64000亿元,同比增长4.2%.将数据"64000"用科学记数法表示为( )
A .0.64x106 B .6.4x105 C .6.4x104 D .64x105
3.2024年7月26日至8月11日在法国巴黎举行第33届夏季奥运会,下列四幅巴黎奥运会项目图标中,是轴对称图形的是( )
4.下列运算正确的是( )
A .5m+ n =5mn B .5m-2m=3 C .3n2+2n3=5n5 D .-m2n+2m2n=m2n
如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=53°,则∠2的度数为( )
A .53° B .47° C .37° D .27°
6.如图,数轴上的A , B 两点分别表示有理数a , b ,下列式子中,不正确的是( )
A . a + b <0 B . a - b <0 C .- a + b >0 D .- b >- a
7.北京时间12月4日,我国申报的"春节﹣﹣中国人庆祝传统新年的社会实践"通过评审,列入联合国教科文组织人类非物质文化遗产代表作名录.现将四张大小相同的正方形卡片拼成如图所示的正方形靶盘(其中两张卡片上是"春"字,另外两张上是"福"字).现向该靶盘随机掷两次飞镖,则两次射中的卡片上的字不相同的概率为( )
A. B. C. D.
8.已知函数 y=中,在每个象限内,y 随 x 的增大而增大,那么它和函数y = kx 在同一直角坐标平面内的大致图象是( )
9.如图,在口ABCD 中,AB =6, AD =9,以点A 为圆心,AB长为半径画弧交AD 于点F ;以点A 为
圆心,适当长为半径画弧分别交AB,AD于M,N两点。分别以点M,N为圆心,大于MN的长为半径画弧,两弧在平行四边形内交于点G ,连接AG 并延长交BC 于点 E ,连接EF , BD , BD 分别交AE , EF 于P , Q 两点,下列结论不正确的是( )
A . AE 平分∠BAD B .四边形 ABEF 是菱形 C.= D . PQ = QD
10.对于二次函数 y =ax2+ bx + c ,规定函数y=是它的相关函数.已知点M , N的坐标分别为(﹣,1),(,1)。连接 MN ,若线段 MN 与二次函数 y =-x2+4x+ n 的相关函数的图象有两个公共点,则 n 的取值范围为( )
A.﹣3<n≤﹣1或1<n≤ B .﹣3<n<﹣1或1≤n≤
C . n ≤-1或1< n ≤ D .-3< n <-1或 n ≥1
二、填空题:本题共5小题,每小题4分,共20分.直接填写答案.
11.分解因式:3ay2-3ax2= 。
12.在一个不透明的口袋中装有3个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 个.
13.已知关于 x 的一元二次方程x2+3x- c =0的两根为2和m ,则m +2的值为 .
14.某市去年居民用水按照4.6元/吨收取费用,为提倡居民节约用水,自今年1月1日起对居民用水实行阶梯水费,规定:若用水超过 a 吨,超过 a 吨的部分每吨增加2元.图中4,12分别表示去年、今年水费 y (元)与用水量 x (吨)之间的关系.实行阶梯水费后,若用水超过 a 吨,则超过 a 吨的部分每吨水费为 元.
15.如图,在矩形ABCD 中,AB =4, BC =8,点E 是射线 BC 上一点,=3,连接 AE ,将△ABE 沿
AE 翻折,得到△AFE ,延长 AF 交 CD 的延长线于点M ,则DM = .
解答题:本大题共10个小题,共90分.解答应写出文字说明、证明过程或演算步骤.
16.(7分)计算:(2025-π)0+4sin45°-(﹣)﹣1+﹣
17.(7分)解不等式组,并写出它的所有整数解.
18.(7分)如图,将平行四边形ABCD 的对角线BD 向两个方向延长,分别至点E 和点F ,且使BE =DF .求证:AE = CF .
19.(8分)小明对笔记本电脑使用角度与高度的舒适性进行了思考与研究.已知笔记本电脑屏幕宽AB =BC =23 cm .笔记本电脑厚度忽略不计.
(1)如图1,小明将笔记本电脑放在水平桌面上,将电脑屏幕打开使∠ABC =110°,求此时电脑屏幕上点A 与桌面的距离;
(2)为改善坐姿守护健康,小明购买了如图2所示的电脑支架,该支架可通过调节支撑杆位置来调整高度.若小明在使用电脑支架时,电脑屏幕始终垂直于桌面,求电脑屏幕打开使∠ABC 分别为110°与120°时,点 A 距离桌面的高度差.(参考数据: sin 70°≈0.9, cos 70°≈0.3)
20.(8分)如图,AB 为⊙O 的直径,直线CP 是⊙O 的切线,切点为C ,过点A 作AD⊥CP ,垂足为D ,交BC 的延长线于点E .
(1)求证:AE = AB ;
(2)若AB =10, BC =6,求线段ED 的长
21.(9分)某校组织学生参加自然科学知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出不完整的统计表和统计图,请根据图表信息解答以下问题.
(1)本次调查抽取了 名参赛学生的成绩,表中 m = 。
(2)直接补全频数分布直方图;
(3)在扇形统计图中," C 组"对应的圆心角的大小是 。
(4)若成绩在90分及以上的为"优秀",请估计该校2000人中有多少同学可以在本次竞赛中获得"优秀".
22.(10分)马面裙作为汉服的重要组成部分,承载着我国深厚的历史文化底蕴.在某网店中,销量最高的A , B 两款马面裙备受消费者青睐,A , B 两款马面裙的售价分别为150元/件和200元/件,两款马面裙3月份的总销量为600件,销售总额为110000元.
(1)求3月份 A , B 两款马面裙的销量分别为多少件?
(2)为满足店铺的日常运营需求,该网店决定从服装厂预定 A , B 两款马面裙共2400件,且A款马面裙的数量不超过B款马面裙数量的,已知A 款马面裙进价为100元/件, B款马面裙进价160元/件,请你设计一种方案,使得这批马面裙全部售出后获利最大,并求出最大利润.
23.(10分)如图,在平面直角坐标系x0y中,直线 y =2x+6与反比例函数 y =的图象交于 A (-1, m ),B 两点,C 为反比例函数图象第四象限上的一点。
(1)求反比例函数的表达式及点 B 的坐标;
(2)当△AOB 与△AOC 的面积相等时,求此时点C 的坐标;
(3)我们把对角线互相垂直且相等的四边形称为"垂等四边形",设点D 是平面内一点,是否存在这样的C , D 两点,使四边形ABCD 是"垂等四边形",且该四边形的两条对角线相交于点Q ,△ABQ ~△ACB ?若存在,求出C , D两点的坐标;若不存在,请说明理由.
24.(12分)如图1,抛物线 y =x2+bx与 x 轴交于点A ,与直线OB 交于点 B (6,6),过点A 作直线OB 的平行线,交抛物线于点 C .
(1)求抛物线 y =x2+ bx 的表达式;
(2)点D 为直线AC 下方抛物线上一点,过点 D作 DE⊥x 轴交直线OB 于点E ,过点E 作 EF⊥AC 于点F ,连接DF .求△DEF 面积的最大值,及此时点D 的坐标;
(3)如图2,在(2)问条件下,将原抛物线向右平移,再次经过(2)问条件下的点D 时,新抛物线与x 轴交于点M , N (M 在N 左侧),与y 轴交于点G ,点P 为新抛物线上的一点,连接DP ,并延长DP 交直线GN 于点H ,使得∠DHN =2∠DGN,写出所有符合条件的点H 的坐标,并写出求解点H 的坐标的其中一种情况的过程.
25.(12分)全等三角形是我们初中数学的重要知识点之一,它为我们学习后面几何知识做好铺垫,掌握全等三角形的证明是做一系列复杂几何证明的基础。
【问题初探】
(1)构造全等三角形的方法有很多,有一种常见的方法是作高线,将需要证明的边或角放在两个直角三角形中进而通过全等证明关系.比如,我们可以通过作高线证明三角形中一个重要的结论"在同一个三角形中,如果两个角相等,那么这两个角所对的边也相等".现在请你完成小聪同学的证明过程;如图1,在△ ABC 中,已知∠B =∠C ,可证 AB = AC ,小聪同学的作法是作 BC 边上的高线 AD .
【类比分析】
(2)通过上述例子,我们发现通过作高线构造直角三角形证明全等确实是一种有效的方法,由此推出了三角形中的重要结论.现在请你借助上述的方法或结论继续探索,如图2,在△ ABC 中,已知∠ABC = ∠ACB ,点E 为边AC 上一点,点F 为边AB 延长线上一点,连接EF 说明理由;与边BC 交于点D ,若点D 恰为线段EF 的中点,试探究线段CE 与线段BF 的数量关系,并说明理由.
【学以致用】
(3)如图3,在△ABC 中,∠CAB =90°, AD , AE 分别为△ABC 的角平分线和中线,过点E 作EF⊥AD 与线段AD 的延长线交于点G ,与边AB 的延长线交于点F ,已知△ABC 的面积是30,线段 AF 的长为8,求△ AED 的面积.
答案
一、选择题:本题共10小题,每小题4分,共40分.每小题只有一个选项符合题目要求.
1.的绝对值是( B )
A .-2025 B . C. D .﹣
2.据中国物流与采购联合会消息,2024年前三季度我国冷链物流总额为64000亿元,同比增长4.2%.将数据"64000"用科学记数法表示为( C )
A .0.64x106 B .6.4x105 C .6.4x104 D .64x105
3.2024年7月26日至8月11日在法国巴黎举行第33届夏季奥运会,下列四幅巴黎奥运会项目图标中,是轴对称图形的是( B )
4.下列运算正确的是( D )
A .5m+ n =5mn B .5m-2m=3 C .3n2+2n3=5n5 D .-m2n+2m2n=m2n
如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=53°,则∠2的度数为( C )
A .53° B .47° C .37° D .27°
6.如图,数轴上的A , B 两点分别表示有理数a , b ,下列式子中,不正确的是( D )
A . a + b <0 B . a - b <0 C .- a + b >0 D .- b >- a
7.北京时间12月4日,我国申报的"春节﹣﹣中国人庆祝传统新年的社会实践"通过评审,列入联合国教科文组织人类非物质文化遗产代表作名录.现将四张大小相同的正方形卡片拼成如图所示的正方形靶盘(其中两张卡片上是"春"字,另外两张上是"福"字).现向该靶盘随机掷两次飞镖,则两次射中的卡片上的字不相同的概率为( A )
A. B. C. D.
8.已知函数 y=中,在每个象限内,y 随 x 的增大而增大,那么它和函数y = kx 在同一直角坐标平面内的大致图象是( B )
9.如图,在口ABCD 中,AB =6, AD =9,以点A 为圆心,AB长为半径画弧交AD 于点F ;以点A 为
圆心,适当长为半径画弧分别交AB,AD于M,N两点。分别以点M,N为圆心,大于MN的长为半径画弧,两弧在平行四边形内交于点G ,连接AG 并延长交BC 于点 E ,连接EF , BD , BD 分别交AE , EF 于P , Q 两点,下列结论不正确的是( D )
A . AE 平分∠BAD B .四边形 ABEF 是菱形 C.= D . PQ = QD
10.对于二次函数 y =ax2+ bx + c ,规定函数y=是它的相关函数.已知点M , N的坐标分别为(﹣,1),(,1)。连接 MN ,若线段 MN 与二次函数 y =-x2+4x+ n 的相关函数的图象有两个公共点,则 n 的取值范围为( A )
A.﹣3<n≤﹣1或1<n≤ B .﹣3<n<﹣1或1≤n≤
C . n ≤-1或1< n ≤ D .-3< n <-1或 n ≥1
二、填空题:本题共5小题,每小题4分,共20分.直接填写答案.
11.分解因式:3ay2-3ax2= 3a(y﹣x)(y+x) 。
12.在一个不透明的口袋中装有3个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 9 个.
13.已知关于 x 的一元二次方程x2+3x- c =0的两根为2和m ,则m +2的值为 ﹣3 .
14.某市去年居民用水按照4.6元/吨收取费用,为提倡居民节约用水,自今年1月1日起对居民用水实行阶梯水费,规定:若用水超过 a 吨,超过 a 吨的部分每吨增加2元.图中4,12分别表示去年、今年水费 y (元)与用水量 x (吨)之间的关系.实行阶梯水费后,若用水超过 a 吨,则超过 a 吨的部分每吨水费为 5.5 元.
15.如图,在矩形ABCD 中,AB =4, BC =8,点E 是射线 BC 上一点,=3,连接 AE ,将△ABE 沿
AE 翻折,得到△AFE ,延长 AF 交 CD 的延长线于点M ,则DM = 或 .
解答题:本大题共10个小题,共90分.解答应写出文字说明、证明过程或演算步骤.
16.(7分)计算:(2025-π)0+4sin45°-(﹣)﹣1+﹣
=1+2+2+2﹣
=3+3
17.(7分)解不等式组,并写出它的所有整数解.
解:由①,得 x >1
由②,得 x ≤4.
所以不等式组的解集为1< x≤4.
所以整数解为2,3,4.
18.(7分)如图,将平行四边形ABCD 的对角线BD 向两个方向延长,分别至点E 和点F ,且使BE =DF .求证:AE = CF .
证明:∵四边形ABCD 为平行四边形,
∴CD = AB , CD∥AB
∴∠ABD = ∠CDB .
∵∠ABD =180°- ∠ABE ,∠CDB =180°- ∠CDF
∴∠ABE = ∠CDF .
在△ ABE 和△ CDF 中
△ABE≌△CDF ( SAS )
∴AE = CF .
19.(8分)小明对笔记本电脑使用角度与高度的舒适性进行了思考与研究.已知笔记本电脑屏幕宽AB =BC =23 cm .笔记本电脑厚度忽略不计.
(1)如图1,小明将笔记本电脑放在水平桌面上,将电脑屏幕打开使∠ABC =110°,求此时电脑屏幕上点A 与桌面的距离;
(2)为改善坐姿守护健康,小明购买了如图2所示的电脑支架,该支架可通过调节支撑杆位置来调整高度.若小明在使用电脑支架时,电脑屏幕始终垂直于桌面,求电脑屏幕打开使∠ABC 分别为110°与120°时,点 A 距离桌面的高度差.(参考数据: sin 70°≈0.9, cos 70°≈0.3)
解:(1)如图1,过点 A作 AD⊥BC ,垂足为 D
∵∠ABC =110°
∴∠ABD =180°-∠ABC =70°.
在 Rt△ABD 中,AB =23 cm
∴AD = AB·sin∠ABD =23xsin70°≈23x0.9=20.7( cm )
∴此时电脑屏幕上点 A 与桌面的距离约为20.7 cm .
如图2,延长AB 交CE 于点 F ,由题意,得BF⊥CE
∴∠BFC =90°.
当∠ABC =120时, ∠CBF =180°-∠ABC =60°
在Rt△BCF 中,BC =23 cm
∴BF = BC·cos 60°=23x=11.5( cm ).
当∠ABC =110°时,∠CBF =180°- ∠ABC =70°
在Rt△BCF 中, BC=23 cm
∴BF = BC·cos 70°≈23x0.3=6.9( cm ),11.5-6.9=4.6( cm ).
∴点 A 距离桌面的高度差约为4.6 cm .
20.(8分)如图,AB 为⊙O 的直径,直线CP 是⊙O 的切线,切点为C ,过点A 作AD⊥CP ,垂足为D ,交BC 的延长线于点E .
(1)求证:AE = AB ;
(2)若AB =10, BC =6,求线段ED 的长
(1)证明:如图,连接OC ,则OC = OB
∴∠B =∠OCB
∵CP 与⊙O 相切于点C
∴CP⊥OC.
∵AD⊥CP
∴AD // OC .
∴∠E = ∠OCB .
∴∠B = ∠E .
∴AE = AB .
(2)解:如图,连接 AC ,AB 为⊙O 的直径,
∴∠ACE = ∠ACB =90°.
∵AE = AB =10, AC⊥BE
∴EC = BC =6.
∵∠CDE = ∠ACE =90°, ∠E = ∠E
∴△CDE∽△ACE .
∴==
∴ED=
21.(9分)某校组织学生参加自然科学知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出不完整的统计表和统计图,请根据图表信息解答以下问题.
(1)本次调查抽取了 名参赛学生的成绩,表中 m = 。
(2)直接补全频数分布直方图;
(3)在扇形统计图中," C 组"对应的圆心角的大小是 。
(4)若成绩在90分及以上的为"优秀",请估计该校2000人中有多少同学可以在本次竞赛中获得"优秀".
解:(1)样本容量为15÷30%=50 m =50-6-9-15=20.
(2)补全频数分布直方图如下:
(3)" C 组"对应的圆心角的大小是360°x30%=108°.
(4)2000x=800(人).
答:估计该校2000人中有800名同学可以在本次竞
22.(10分)马面裙作为汉服的重要组成部分,承载着我国深厚的历史文化底蕴.在某网店中,销量最高的A , B 两款马面裙备受消费者青睐,A , B 两款马面裙的售价分别为150元/件和200元/件,两款马面裙3月份的总销量为600件,销售总额为110000元.
(1)求3月份 A , B 两款马面裙的销量分别为多少件?
(2)为满足店铺的日常运营需求,该网店决定从服装厂预定 A , B 两款马面裙共2400件,且A款马面裙的数量不超过B款马面裙数量的,已知A 款马面裙进价为100元/件, B款马面裙进价160元/件,请你设计一种方案,使得这批马面裙全部售出后获利最大,并求出最大利润.
解:(1)设3月份A 款马面裙的销量为x 件,B 款马面裙的销量为y 件
由题意,得,解得
答:3月份 A 款马面裙的销量为200件, B 款马面裙的销量为400件.
(2)设网店购进 A 款马面裙 a 件,再购进 B 款马面裙(2400- a )件,总利润为 w 元,
a≤(2400- a ),解得 a≤800
由题意,得 w =(150-100) a +(200-160)(2400- a )=10a+96000,
∵10>0
∴w 随 a 的增大而增大.
当 a =800时,w 取最大值,
w的最大值=10x800+96000=104000.
此时2400- x =2400-800=1600.
答:网店购进 A 款马面裙800件, B 款马面裙1600件,获利最大,最大利润为104000元.
23.(10分)如图,在平面直角坐标系x0y中,直线 y =2x+6与反比例函数 y =的图象交于 A (-1, m ),B 两点,C 为反比例函数图象第四象限上的一点。
(1)求反比例函数的表达式及点 B 的坐标;
(2)当△AOB 与△AOC 的面积相等时,求此时点C 的坐标;
(3)我们把对角线互相垂直且相等的四边形称为"垂等四边形",设点D 是平面内一点,是否存在这样的C , D 两点,使四边形ABCD 是"垂等四边形",且该四边形的两条对角线相交于点Q ,△ABQ ~△ACB ?若存在,求出C , D两点的坐标;若不存在,请说明理由.
解:(1)当x =-1时, y =2x+6=4,即点 A (-1,4),将点 A 的坐标代人反比例函数的表达式,得 k=-1x4=-4
即反比例函数的表达式为 y =﹣
联立两个函数表达式,得﹣=2x+6
解得x =-1或﹣2,即B (-2,2).
(2)由A , B 的坐标,得 S△AOB =3,设 C ( n ,﹣)
由点A , C 的坐标,得直线AC 的函数表达式为 y =﹣(x+1)+4
设直线 AC 交 y 轴于点H (0,4-)
则△AOC 的面积= ×(n+1)=3
解得 n =2或
C1(2,-2), C2 (,-8).
(3)C(4,﹣1) D(3,7)
24.(12分)如图1,抛物线 y =x2+bx与 x 轴交于点A ,与直线OB 交于点 B (6,6),过点A 作直线OB 的平行线,交抛物线于点 C .
(1)求抛物线 y =x2+ bx 的表达式;
(2)点D 为直线AC 下方抛物线上一点,过点 D作 DE⊥x 轴交直线OB 于点E ,过点E 作 EF⊥AC 于点F ,连接DF .求△DEF 面积的最大值,及此时点D 的坐标;
(3)如图2,在(2)问条件下,将原抛物线向右平移,再次经过(2)问条件下的点D 时,新抛物线与x 轴交于点M , N (M 在N 左侧),与y 轴交于点G ,点P 为新抛物线上的一点,连接DP ,并延长DP 交直线GN 于点H ,使得∠DHN =2∠DGN,写出所有符合条件的点H 的坐标,并写出求解点H 的坐标的其中一种情况的过程.
解:(1)将点 B 的坐标代人函数表达式,得6=36+6b,解得 b =-5.
∴抛物线的表达式为 y =x2-5x.
(2)由抛物线的表达式,得点 A (5,0),由点 B 的坐标,得直线OB 的表达式为y = x
∵FC // OB且直线 FC 过点 A
∴直线 FC 的表达式为 y = x -5.
设点E ( m , m ),则点D ( m ,m2-5m), Q ( m , m -5).
∴DE =-m2+6m, EQ =5.
如图1,过点 F 作 FW⊥ED 于点 W ,EF⊥OB , OB 和水平线的夹角为45°,
∴△EFW为等腰直角三角形.
同理可得△FWQ 为等腰直角三角形,
∴FW =EQ=
∴△DEF面积=﹣(m﹣3)2+
即△ DEF 面积的最大值为,此时m =3,点 D 的坐标为(3,-6).
(3)H(,)或(,﹣)
25.(12分)全等三角形是我们初中数学的重要知识点之一,它为我们学习后面几何知识做好铺垫,掌握全等三角形的证明是做一系列复杂几何证明的基础。
【问题初探】
(1)构造全等三角形的方法有很多,有一种常见的方法是作高线,将需要证明的边或角放在两个直角三角形中进而通过全等证明关系.比如,我们可以通过作高线证明三角形中一个重要的结论"在同一个三角形中,如果两个角相等,那么这两个角所对的边也相等".现在请你完成小聪同学的证明过程;如图1,在△ ABC 中,已知∠B =∠C ,可证 AB = AC ,小聪同学的作法是作 BC 边上的高线 AD .
【类比分析】
(2)通过上述例子,我们发现通过作高线构造直角三角形证明全等确实是一种有效的方法,由此推出了三角形中的重要结论.现在请你借助上述的方法或结论继续探索,如图2,在△ ABC 中,已知∠ABC = ∠ACB ,点E 为边AC 上一点,点F 为边AB 延长线上一点,连接EF 说明理由;与边BC 交于点D ,若点D 恰为线段EF 的中点,试探究线段CE 与线段BF 的数量关系,并说明理由.
【学以致用】
(3)如图3,在△ABC 中,∠CAB =90°, AD , AE 分别为△ABC 的角平分线和中线,过点E 作EF⊥AD 与线段AD 的延长线交于点G ,与边AB 的延长线交于点F ,已知△ABC 的面积是30,线段 AF 的长为8,求△ AED 的面积.
(1)证明:∵AD 是△ ABC 的高线,
∴∠ADB = ∠ADC =90°.
∵AD = AD , ∠B = ∠C
∴△ADB≌△ADC ( AAS ).
∴AB = AC .
(2)解: CE = BF ,
理由:过点 E 作 EG∥AB 交 BC 于点 G ,
∴∠F=∠DEG,∠FBD=∠EGD
∵点 D 恰为线段 EF 的中点
∴DF = DE
∴△BFD≌ GED ( AAS )
∴BF = EG
∵∠ABC =∠ACB
∴∠BGC =∠ECG
∴EG = CE
∴CE = BF
(3)
同课章节目录
