9.1.2 用坐标描述简单几何图形 同步练习 2024-2025学年下学期初中数学人教版七年级下册(新教材)
文档属性
| 名称 | 9.1.2 用坐标描述简单几何图形 同步练习 2024-2025学年下学期初中数学人教版七年级下册(新教材) | 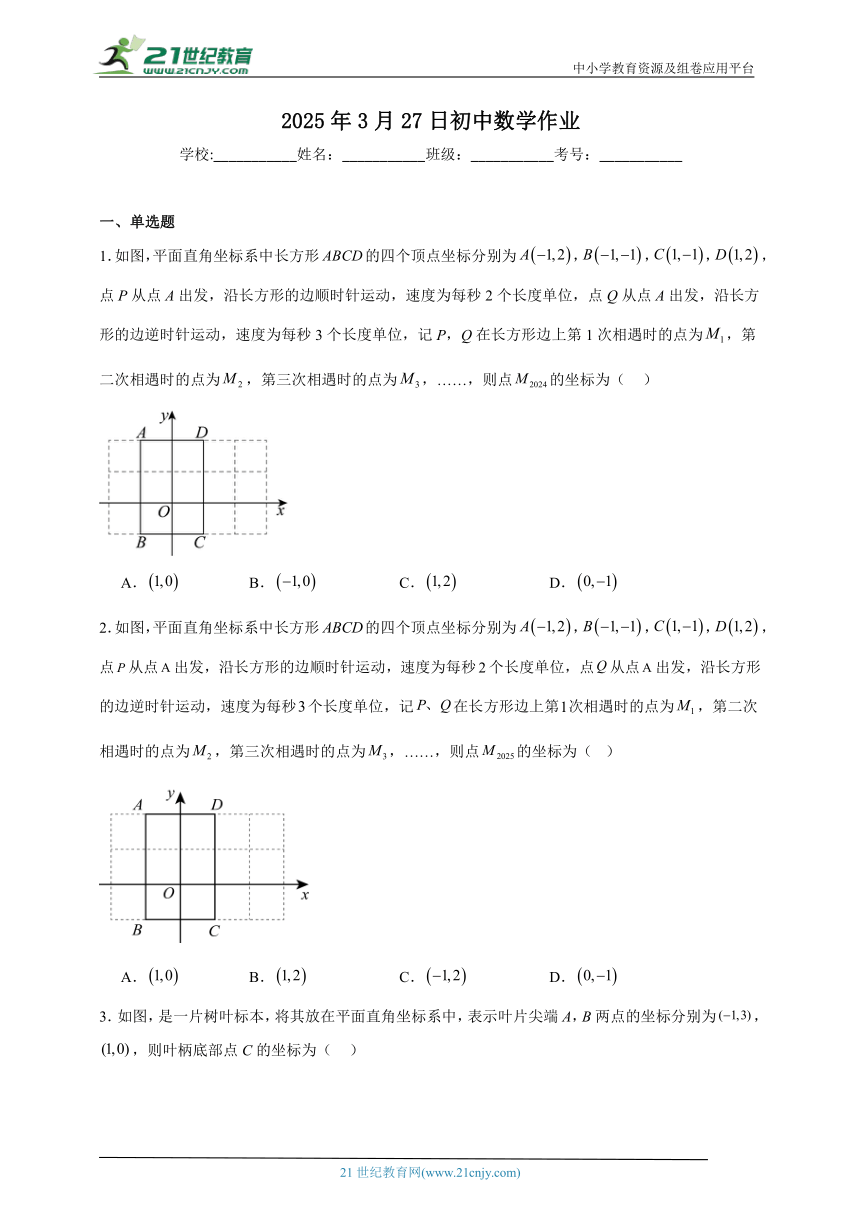 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 16:39:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年3月27日初中数学作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,平面直角坐标系中长方形的四个顶点坐标分别为,,,,点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个长度单位,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个长度单位,记P,Q在长方形边上第1次相遇时的点为,第二次相遇时的点为,第三次相遇时的点为,……,则点的坐标为( )
A. B. C. D.
2.如图,平面直角坐标系中长方形的四个顶点坐标分别为,,,,点从点出发,沿长方形的边顺时针运动,速度为每秒个长度单位,点从点出发,沿长方形的边逆时针运动,速度为每秒个长度单位,记在长方形边上第次相遇时的点为,第二次相遇时的点为,第三次相遇时的点为,……,则点的坐标为( )
A. B. C. D.
3.如图,是一片树叶标本,将其放在平面直角坐标系中,表示叶片尖端A,B两点的坐标分别为,,则叶柄底部点C的坐标为( )
A. B. C. D.
4.如图是一只蝴蝶标本,已知表示蝴蝶两“翅膀尾部”A,B 两点的坐标分别为(-2,-3),(2,-3),则表示蝴蝶身体“尾部”C 点的坐标为( )
A.(0,-1) B.(1,-1) C.(-1,0) D.(2,-1)
5.如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿.将其放在平面直角坐标系中,表示叶片“顶部”A、B两点的坐标分别为、,则叶杆“底部”点C的坐标为( )
A. B. C. D.
6.在平面直角坐标系中,依次描出下列各点,并将各组内的点依次连接起来:
(1)(2,1),(2,0),(3,0),(3,4);
(2)(3,6),(0,4),(6,4),(3,6).
你发现所得的图形是( )
A.两个三角形 B.房子 C.雨伞 D.电灯
7.如图所示,长方形的两边、分别在x轴、y轴上,点C与原点重合,点,将长方形沿x轴无滑动向右翻滚,经过一次翻滚,点A的对应点记为;经过第二次翻滚,点A的对应点记为;……,依次类推,经过第2023次翻滚,点A的对应点的坐标为( )
A. B. C. D.
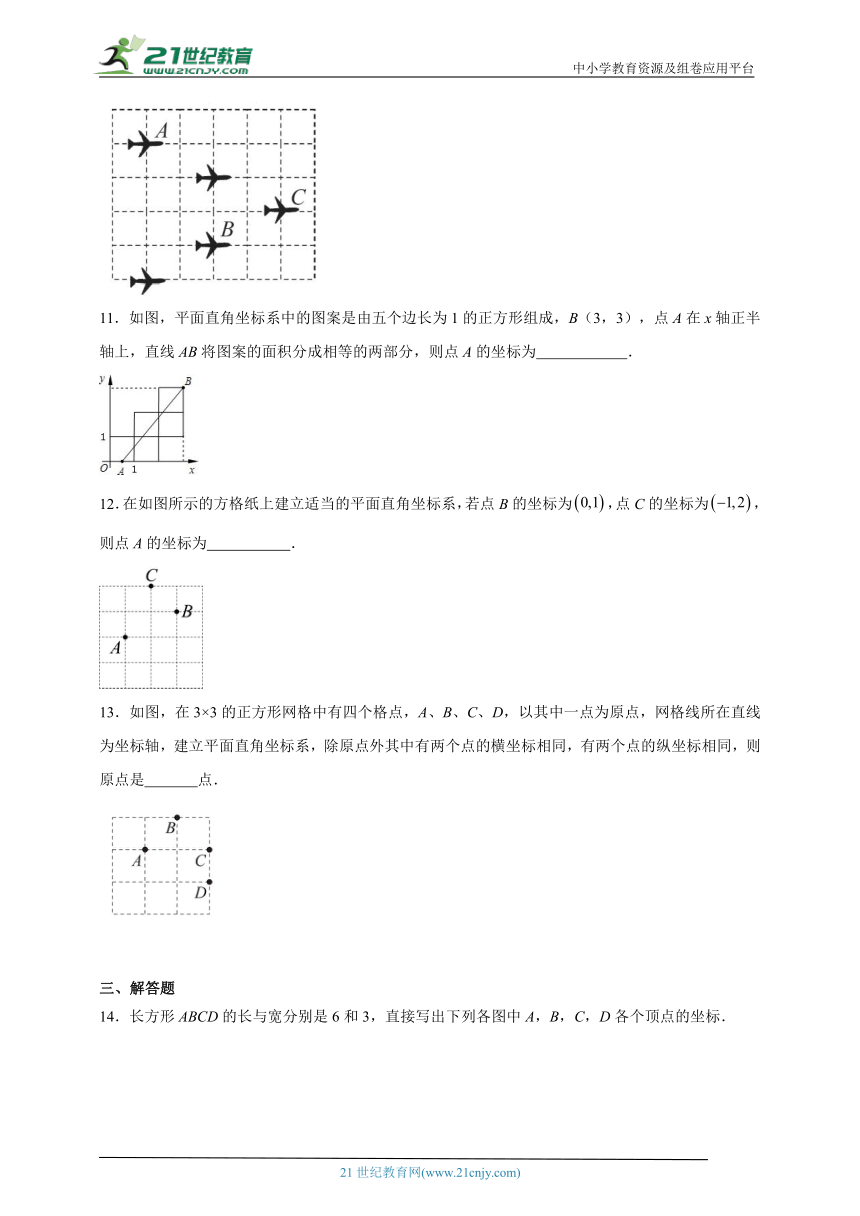
8.“歼-20”是我国自主研制的第五代战斗机.如图,小明将一张“歼-20”一飞冲天的图片放入网格中,若图片上点B的坐标为,点C的坐标为,则点A的坐标为( )
A. B. C. D.
二、填空题
9.如图,已知长方形的长等于5,宽等于3,则点的坐标为 .
10.如图是轰炸机机群的一个飞行队形,如果建立一个平面直角坐标系,此时轰炸机A,B的位置的坐标分别为,那么轰炸机C的位置的坐标是 .
11.如图,平面直角坐标系中的图案是由五个边长为1的正方形组成,B(3,3),点A在x轴正半轴上,直线AB将图案的面积分成相等的两部分,则点A的坐标为 .
12.在如图所示的方格纸上建立适当的平面直角坐标系,若点B的坐标为,点C的坐标为,则点A的坐标为 .
13.如图,在3×3的正方形网格中有四个格点,A、B、C、D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,除原点外其中有两个点的横坐标相同,有两个点的纵坐标相同,则原点是 点.
三、解答题
14.长方形ABCD的长与宽分别是6和3,直接写出下列各图中A,B,C,D各个顶点的坐标.
15.如图,在长方形中,O为平面直角坐标系的原点,点A的坐标为,点C的坐标为,且a,b满足,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着折线线路运动一周停止.
备用图
(1)求点B的坐标;
(2)在移动过程中,当点P到y轴的距离为4个单位长度时,求点P移动的时间;
(3)当点P在的线路上移动时,是否存在点P使的面积是12,若存在,直接写出点P的坐标;若不存在,请说明理由.
16.如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8,AD=BC=6,D点与原点重合,坐标为(0,0).
(1)点B的坐标为__________;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t=__________时,BP=CQ;
(3)在(2)的条件下,当Q运动到某一位置时,△ADQ的面积为9,求此时Q点的坐标.
17.在直角坐标系中描出各组点,并将各组内的点用线段依次连接起来.
①,,,;
②,,,;
③,,,.
(1)观察得到的图形,你觉得它像什么?
(2)找出图象上位于坐标轴上的点,与同伴进行交流;
(3)上面三组点分别位于哪个象限,你是如何判断的?
(4)图形上一些点之间具有特殊的位置关系,找出几对,它们的坐标有何特点?说说你的发现.
18.在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接.
(1),,,;
(2),,,;
观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段EC与x轴有什么位置关系?点E和点C的坐标有什么特点?线段EC上其他点的坐标呢?
(3)点F和点G的横坐标有什么共同特点?线段FG与y轴有怎样的位置?
《2025年3月27日初中数学作业》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A D A D C B A
1.D
【分析】本题主要考查了平面直角坐标系中点的坐标变换.根据点坐标计算长方形的周长为,设经过t秒P,Q第一次相遇,则P点走的路程为,Q点走的路程为,根据题意列方程,即可求出经过2秒第一次相遇,进一步求出第一次、第二次、第三次……相遇点的坐标,直到找出五次相遇一循环,再用的余数即可求出第2024次相遇点的坐标.
【详解】解:长方形的周长为,
设经过t秒P,Q第一次相遇,则P点走的路程为,Q点走的路程为,
根据题意得,
解得,
∴当时,P、Q第一次相遇,此时相遇点坐标为,
当时,P、Q第二次相遇,此时相遇点坐标为,
当时,P、Q第三次相遇,此时相遇点坐标为,
当时,P、Q第四次相遇,此时相遇点坐标为,
当时,P、Q第五次相遇,此时相遇点坐标为,
当时,P、Q第六次相遇,此时相遇点坐标为,
∴五次相遇一循环,
∵,
∴的坐标为.
故选:D.
2.A
【分析】本题考查了平面直角坐标系中点坐标的规律,长方形的性质,根据点坐标可得长方形的周长,设运动时间为,由行程问题的数量关系可得,由此可得每次相遇的时间,从而找出规律计算即可求解,掌握行程中的数量关系,平面直角坐标系中点坐标运动规律是解题的关键.
【详解】解:∵长方形的四个顶点坐标分别为,,,,
∴,,
∴长方形的周长为,
设运动时间为,
∴,
解得,,
∴当时,点第一次相遇,则点走的路程为,即在的正半轴上,
∴点;
当时,点第二次相遇,则点走的路程为,即在的付半轴上,
∴点;
当时,点第三次相遇,则点走的路程为,即在的付半轴上,
∴点;
当时,点第四次相遇,则点走的路程为,即在的付半轴上,
∴点;
当时,点第五次相遇,则点走的路程为,即在的付半轴上,
∴点;
当时,点第六次相遇,则点走的路程为,即在的付半轴上,
∴点;
∴五次相遇一循环,
∴,
∴点,
故选:A .
3.D
【分析】本题考查了实际问题中用坐标表示位置,根据点与点的相对位置即可求解.
【详解】解:由图可知:点向右移动3个单位长度,向上移动1个单位长度即可得到点,
故点C的坐标为,即:,
故选:D
4.A
【分析】根据已知A、B两点坐标确定坐标系,然后确定C点位置.
【详解】解:由A、B 两点的坐标(-2,-3)、(2,-3),可得出坐标轴如下图所示:
所以C 点的坐标为(0,-1).
故选:A
【点睛】本题主要考查了用坐标确定位置,依据已知点的坐标确定出坐标轴的位置是解题关键.
5.D
【分析】根据,两点的坐标分别为,,可以判断原点的位置,然后确定点坐标即可.
【详解】解:∵,两点的坐标分别为,,
∴点向右移动2个单位即为原点的位置,
如图所示,
∴点的坐标为:,
故选:D.
【点睛】本题主要考查在平面直角系中,根据已知点的坐标,求未知点的坐标,解题的关键是根据已知点的坐标确定原点的坐标.
6.C
【详解】根据题意,依次描点画线,得到如下的图形,故选C.
7.B
【分析】观察图形即可得到经过4次翻滚后点A对应点一循环,先求出的商和余数,从而解答本题.
【详解】解:如图所示:
观察图形可得经过4次翻滚后点A对应点一循环,
,
∵点,长方形的周长为:,
,
∴经过505次翻滚后点A对应点的坐标为,即.
故选:B.
【点睛】本题考查探究点的坐标的问题,关键是找到点的变化规律.
8.A
【分析】本题主要考查了坐标与图形,解题的关键是根据已知点的坐标,建立平面直角坐标系.
根据点的坐标为,点的坐标为建立平面直角坐标系,得出点的坐标即可.
【详解】解:∵点的坐标为,点的坐标为,
∴建立如图所示的平面直角坐标系,
∴点的坐标为,故A正确.
故选:A.
9.
【分析】根据点B在坐标系中的位置即可得出结论.
【详解】解:由平面直角坐标系可知点的坐标为.
故答案为:.
【点睛】本题考查的是点的坐标,是基础题.
10.
【分析】先根据点和点的坐标建立平面直角坐标系,再结合图形得出答案.
【详解】解:根据题意可建立如图所示平面直角坐标系
由图可知轰炸机的坐标是,
故答案为:.
【点睛】本题主要考查坐标确定位置,解题的关键是根据已知点的坐标建立平面直角坐标系.
11.
【分析】过点B作轴于点C,然后根据三角形面积公式表示出被分成相等的两部分的面积即可求解.
【详解】过点B作轴于点C,如下图:
平面直角坐标系中图案是由五个边长为1的正方形组成,
每个正方形的面积为:,
该图案的面积为:,
直线AB将图案的面积分成相等的两部分,
一部分的面积为:,
点B的坐标为(3,3),
,
点A在x轴正半轴上,
,
,
,
,
点A的坐标为.
【点睛】本题考查了三角形面积、坐标与图形性质,作辅助线补成规则图形表示出分成两部分的面积是解题关键.
12.
【分析】本题考查平面直角坐标系、在坐标系中确定点的坐标,根据点B,C的坐标可确定原点的位置,再作平面直角坐标系即可,从而可确定点A的坐标.
【详解】解:建立平面直角坐标系如图所示:
∴点A的坐标为,
故答案为:.
13.B
【详解】由网格的特点可得,点A和点C的纵坐标相同,点C与点D的横坐标相同,
∴点B为原点.
故答案为:B.
【点睛】本题考查了与x轴、y轴平行的直线上点的坐标特点,掌握平面直角坐标系内点的坐标的确定方法是解题的关键.
14.,,,.
【分析】根据长方形的长与宽的长度和长方形在坐标系中的位置即可求解.
【详解】∵长方形ABCD的长与宽分别是6和3,
∴CD=6,AD=BC=3,
又由图可得,C在x轴负半轴上,D在x轴正半轴上,点A在第一象限,点B在第二象限,
∴,,,.
【点睛】此题考查了坐标系中点的坐标表示,解题的关键是熟练掌握坐标系中点的坐标表示方法.
15.(1)
(2)6秒或12秒
(3)存在,P点的坐标为或
【分析】此题考查平面直角坐标系中点的图形与坐标、非负数的性质、动点问题,一元一次方程的应用,学会分类思想是解题的关键.
(1)先根据非负数的性质求得a,b, 则,,根据长方形的性质可求得点B的坐标.
(2)设点P移动的时间为t秒,点到轴的距离为个单位长度,则点P在边上或在边上,分别列方程求出t的值即可;
(3)分两种情况,当点P在边上时,则;当点P在边上时,则,分别求出,进一步即可得出点B的坐标.
【详解】(1)解:∵,
∴,,
∴,,
∴,,
∵四边形是长方形,
∴,
∴轴,轴,
∴
(2)设点P移动的时间为t秒,
∵点P到y轴的距离为4个单位长度,
∴点P在边上或在边上,
当点P在边长上,
则,
解得:,
当点P在边上,
则,
解得:.
(3)当点P在边上时,如下图:
∵,,
∴,
解得:,
∴点P的坐标为:
当点P在边上时,如下图:
∵,,
∴,
∴,
∴.
综上:否存在点P使的面积是12,此时,P点的坐标为或.
16.(1)(8,6)
(2)
(3)点Q的坐标为(3,0)或(-3,0).
【分析】(1)根据四边形ABCD是长方形,且D点与原点重合,点A在y轴上,点C在x轴上,AB=CD=8,AD=BC=6,可直接写出点B的坐标;
(2)由BP=8-3t,CQ=4t,列方程求出t的值即可;
(3)设点Q的坐标为(x,0),分两种情况讨论,一是点Q在线段CO上,则OQ=x,二是点Q在线段CO的延长线上,则OQ=-x,根据△ADQ的面积为9分别列方程求出相应的x的值即可.
【详解】(1)解:∵四边形ABCD是长方形,且D点与原点重合,点A在y轴上,点C在x轴上,AB=CD=8,AD=BC=6,
∴点B的坐标为(8,6),
故答案为:(8,6);
(2)解:根据题意,AP=3t,CQ=4t,
∴BP=8-3t,
∵BP=CQ,
∴8-3t=4t,
解得:t=;
故答案为:;
(3)解:设点Q的坐标为(x,0),
当点Q在线段CO上时,如图2,
∴OQ=x,
∵S△ADQ=AD OQ=9,
∴×6x=9,
解得x=3,
∴OQ=3,
∴Q(3,0);
当点Q在线段CO的延长线上,如图3,
∴OQ=-x,
∵S△ADQ=AD OQ=9,
∴×6(-x)=9,
解得x=-3,
∴OQ=3,
∴Q(-3,0),
综上所述,当点Q运动到距原点3个单位长度时,△ADQ的面积为9,此时点Q的坐标为(3,0)或(-3,0).
【点睛】此题考查了坐标与图形的性质,解题过程中还涉及数形结合、分类讨论等数学思想的运用,用含未知数的式子表示运动过程中线段的长是解题的关键.
17.(1)像一棵树;(2)x轴上的点有:,,,;y轴上的点有:;(3)点,,,在第一象限内,因为它们的横坐标与纵坐标都是正实数;点,在第四象限内,因为它们的横坐标是正实数,纵坐标是负实数;(4)点与的纵坐标相同,它们的连线段与x轴平行;点,,的横坐标相同,它们的连线段与y轴平行.
【分析】(1)依此描出各组点的坐标,然后依此连接,由图象可进行求解;
(2)根据图象可直接进行求解;
(3)根据平面直角坐标系中象限的符号特点可直接进行求解;
(4)根据图象可直接进行求解.
【详解】解:(1)描出各组点的坐标并依此连接,如图所示:
由图象可知:像一棵树;
(2)x轴上的点有:,,,;y轴上的点有:;
(3)点,,,在第一象限内,因为它们的横坐标与纵坐标都是正实数;点,在第四象限内,因为它们的横坐标是正实数,纵坐标是负实数;
(4)学生的发现可以多样.例如,点与的纵坐标相同,它们的连线段与x轴平行;点,,的横坐标相同,它们的连线段与y轴平行.
【点睛】本题主要考查平面直角坐标系,解题的关键是在平面直角坐标系中描出各点的坐标.
18.连接起来的图形像“房子”;(1)线段AG上的点都在x轴上,它们的纵坐标都等于0;线段AB上的点、线段CD与y轴的交点,它们都在y轴上,它们的横坐标都等于0;(2)线段EC平行于x轴,点E和点C的纵坐标相同.线段EC上其他点的纵坐标也相同,都是3;(3)点F和点G的横坐标相同.线段FG与y轴平行.
【分析】在坐标系中描出各点,再顺次连接可得一个房子的图案;
(1)结合图案分析,即可得出答案;
(2)结合图案分析,即可得出答案;
(3)结合图案分析,即可得出答案;
【详解】连接起来的图形像“房子”.
(1)线段AG上的点都在x轴上,它们的纵坐标都等于0;线段AB上的点、线段CD与y轴的交点,它们都在y轴上,它们的横坐标都等于0.
(2)线段EC平行于x轴,点E和点C的纵坐标相同.线段EC上其他点的纵坐标也相同,都是3.
(3)点F和点G的横坐标相同.线段FG与y轴平行.
【点睛】本题主要考查坐标与图形的性质,作图的关键是根据点的坐标确定点在平面直角坐标系中的位置,并根据位置依次连接,形成题目中要求的图形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年3月27日初中数学作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,平面直角坐标系中长方形的四个顶点坐标分别为,,,,点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个长度单位,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个长度单位,记P,Q在长方形边上第1次相遇时的点为,第二次相遇时的点为,第三次相遇时的点为,……,则点的坐标为( )
A. B. C. D.
2.如图,平面直角坐标系中长方形的四个顶点坐标分别为,,,,点从点出发,沿长方形的边顺时针运动,速度为每秒个长度单位,点从点出发,沿长方形的边逆时针运动,速度为每秒个长度单位,记在长方形边上第次相遇时的点为,第二次相遇时的点为,第三次相遇时的点为,……,则点的坐标为( )
A. B. C. D.
3.如图,是一片树叶标本,将其放在平面直角坐标系中,表示叶片尖端A,B两点的坐标分别为,,则叶柄底部点C的坐标为( )
A. B. C. D.
4.如图是一只蝴蝶标本,已知表示蝴蝶两“翅膀尾部”A,B 两点的坐标分别为(-2,-3),(2,-3),则表示蝴蝶身体“尾部”C 点的坐标为( )
A.(0,-1) B.(1,-1) C.(-1,0) D.(2,-1)
5.如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿.将其放在平面直角坐标系中,表示叶片“顶部”A、B两点的坐标分别为、,则叶杆“底部”点C的坐标为( )
A. B. C. D.
6.在平面直角坐标系中,依次描出下列各点,并将各组内的点依次连接起来:
(1)(2,1),(2,0),(3,0),(3,4);
(2)(3,6),(0,4),(6,4),(3,6).
你发现所得的图形是( )
A.两个三角形 B.房子 C.雨伞 D.电灯
7.如图所示,长方形的两边、分别在x轴、y轴上,点C与原点重合,点,将长方形沿x轴无滑动向右翻滚,经过一次翻滚,点A的对应点记为;经过第二次翻滚,点A的对应点记为;……,依次类推,经过第2023次翻滚,点A的对应点的坐标为( )
A. B. C. D.
8.“歼-20”是我国自主研制的第五代战斗机.如图,小明将一张“歼-20”一飞冲天的图片放入网格中,若图片上点B的坐标为,点C的坐标为,则点A的坐标为( )
A. B. C. D.
二、填空题
9.如图,已知长方形的长等于5,宽等于3,则点的坐标为 .
10.如图是轰炸机机群的一个飞行队形,如果建立一个平面直角坐标系,此时轰炸机A,B的位置的坐标分别为,那么轰炸机C的位置的坐标是 .
11.如图,平面直角坐标系中的图案是由五个边长为1的正方形组成,B(3,3),点A在x轴正半轴上,直线AB将图案的面积分成相等的两部分,则点A的坐标为 .
12.在如图所示的方格纸上建立适当的平面直角坐标系,若点B的坐标为,点C的坐标为,则点A的坐标为 .
13.如图,在3×3的正方形网格中有四个格点,A、B、C、D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,除原点外其中有两个点的横坐标相同,有两个点的纵坐标相同,则原点是 点.
三、解答题
14.长方形ABCD的长与宽分别是6和3,直接写出下列各图中A,B,C,D各个顶点的坐标.
15.如图,在长方形中,O为平面直角坐标系的原点,点A的坐标为,点C的坐标为,且a,b满足,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着折线线路运动一周停止.
备用图
(1)求点B的坐标;
(2)在移动过程中,当点P到y轴的距离为4个单位长度时,求点P移动的时间;
(3)当点P在的线路上移动时,是否存在点P使的面积是12,若存在,直接写出点P的坐标;若不存在,请说明理由.
16.如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8,AD=BC=6,D点与原点重合,坐标为(0,0).
(1)点B的坐标为__________;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t=__________时,BP=CQ;
(3)在(2)的条件下,当Q运动到某一位置时,△ADQ的面积为9,求此时Q点的坐标.
17.在直角坐标系中描出各组点,并将各组内的点用线段依次连接起来.
①,,,;
②,,,;
③,,,.
(1)观察得到的图形,你觉得它像什么?
(2)找出图象上位于坐标轴上的点,与同伴进行交流;
(3)上面三组点分别位于哪个象限,你是如何判断的?
(4)图形上一些点之间具有特殊的位置关系,找出几对,它们的坐标有何特点?说说你的发现.
18.在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接.
(1),,,;
(2),,,;
观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段EC与x轴有什么位置关系?点E和点C的坐标有什么特点?线段EC上其他点的坐标呢?
(3)点F和点G的横坐标有什么共同特点?线段FG与y轴有怎样的位置?
《2025年3月27日初中数学作业》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A D A D C B A
1.D
【分析】本题主要考查了平面直角坐标系中点的坐标变换.根据点坐标计算长方形的周长为,设经过t秒P,Q第一次相遇,则P点走的路程为,Q点走的路程为,根据题意列方程,即可求出经过2秒第一次相遇,进一步求出第一次、第二次、第三次……相遇点的坐标,直到找出五次相遇一循环,再用的余数即可求出第2024次相遇点的坐标.
【详解】解:长方形的周长为,
设经过t秒P,Q第一次相遇,则P点走的路程为,Q点走的路程为,
根据题意得,
解得,
∴当时,P、Q第一次相遇,此时相遇点坐标为,
当时,P、Q第二次相遇,此时相遇点坐标为,
当时,P、Q第三次相遇,此时相遇点坐标为,
当时,P、Q第四次相遇,此时相遇点坐标为,
当时,P、Q第五次相遇,此时相遇点坐标为,
当时,P、Q第六次相遇,此时相遇点坐标为,
∴五次相遇一循环,
∵,
∴的坐标为.
故选:D.
2.A
【分析】本题考查了平面直角坐标系中点坐标的规律,长方形的性质,根据点坐标可得长方形的周长,设运动时间为,由行程问题的数量关系可得,由此可得每次相遇的时间,从而找出规律计算即可求解,掌握行程中的数量关系,平面直角坐标系中点坐标运动规律是解题的关键.
【详解】解:∵长方形的四个顶点坐标分别为,,,,
∴,,
∴长方形的周长为,
设运动时间为,
∴,
解得,,
∴当时,点第一次相遇,则点走的路程为,即在的正半轴上,
∴点;
当时,点第二次相遇,则点走的路程为,即在的付半轴上,
∴点;
当时,点第三次相遇,则点走的路程为,即在的付半轴上,
∴点;
当时,点第四次相遇,则点走的路程为,即在的付半轴上,
∴点;
当时,点第五次相遇,则点走的路程为,即在的付半轴上,
∴点;
当时,点第六次相遇,则点走的路程为,即在的付半轴上,
∴点;
∴五次相遇一循环,
∴,
∴点,
故选:A .
3.D
【分析】本题考查了实际问题中用坐标表示位置,根据点与点的相对位置即可求解.
【详解】解:由图可知:点向右移动3个单位长度,向上移动1个单位长度即可得到点,
故点C的坐标为,即:,
故选:D
4.A
【分析】根据已知A、B两点坐标确定坐标系,然后确定C点位置.
【详解】解:由A、B 两点的坐标(-2,-3)、(2,-3),可得出坐标轴如下图所示:
所以C 点的坐标为(0,-1).
故选:A
【点睛】本题主要考查了用坐标确定位置,依据已知点的坐标确定出坐标轴的位置是解题关键.
5.D
【分析】根据,两点的坐标分别为,,可以判断原点的位置,然后确定点坐标即可.
【详解】解:∵,两点的坐标分别为,,
∴点向右移动2个单位即为原点的位置,
如图所示,
∴点的坐标为:,
故选:D.
【点睛】本题主要考查在平面直角系中,根据已知点的坐标,求未知点的坐标,解题的关键是根据已知点的坐标确定原点的坐标.
6.C
【详解】根据题意,依次描点画线,得到如下的图形,故选C.
7.B
【分析】观察图形即可得到经过4次翻滚后点A对应点一循环,先求出的商和余数,从而解答本题.
【详解】解:如图所示:
观察图形可得经过4次翻滚后点A对应点一循环,
,
∵点,长方形的周长为:,
,
∴经过505次翻滚后点A对应点的坐标为,即.
故选:B.
【点睛】本题考查探究点的坐标的问题,关键是找到点的变化规律.
8.A
【分析】本题主要考查了坐标与图形,解题的关键是根据已知点的坐标,建立平面直角坐标系.
根据点的坐标为,点的坐标为建立平面直角坐标系,得出点的坐标即可.
【详解】解:∵点的坐标为,点的坐标为,
∴建立如图所示的平面直角坐标系,
∴点的坐标为,故A正确.
故选:A.
9.
【分析】根据点B在坐标系中的位置即可得出结论.
【详解】解:由平面直角坐标系可知点的坐标为.
故答案为:.
【点睛】本题考查的是点的坐标,是基础题.
10.
【分析】先根据点和点的坐标建立平面直角坐标系,再结合图形得出答案.
【详解】解:根据题意可建立如图所示平面直角坐标系
由图可知轰炸机的坐标是,
故答案为:.
【点睛】本题主要考查坐标确定位置,解题的关键是根据已知点的坐标建立平面直角坐标系.
11.
【分析】过点B作轴于点C,然后根据三角形面积公式表示出被分成相等的两部分的面积即可求解.
【详解】过点B作轴于点C,如下图:
平面直角坐标系中图案是由五个边长为1的正方形组成,
每个正方形的面积为:,
该图案的面积为:,
直线AB将图案的面积分成相等的两部分,
一部分的面积为:,
点B的坐标为(3,3),
,
点A在x轴正半轴上,
,
,
,
,
点A的坐标为.
【点睛】本题考查了三角形面积、坐标与图形性质,作辅助线补成规则图形表示出分成两部分的面积是解题关键.
12.
【分析】本题考查平面直角坐标系、在坐标系中确定点的坐标,根据点B,C的坐标可确定原点的位置,再作平面直角坐标系即可,从而可确定点A的坐标.
【详解】解:建立平面直角坐标系如图所示:
∴点A的坐标为,
故答案为:.
13.B
【详解】由网格的特点可得,点A和点C的纵坐标相同,点C与点D的横坐标相同,
∴点B为原点.
故答案为:B.
【点睛】本题考查了与x轴、y轴平行的直线上点的坐标特点,掌握平面直角坐标系内点的坐标的确定方法是解题的关键.
14.,,,.
【分析】根据长方形的长与宽的长度和长方形在坐标系中的位置即可求解.
【详解】∵长方形ABCD的长与宽分别是6和3,
∴CD=6,AD=BC=3,
又由图可得,C在x轴负半轴上,D在x轴正半轴上,点A在第一象限,点B在第二象限,
∴,,,.
【点睛】此题考查了坐标系中点的坐标表示,解题的关键是熟练掌握坐标系中点的坐标表示方法.
15.(1)
(2)6秒或12秒
(3)存在,P点的坐标为或
【分析】此题考查平面直角坐标系中点的图形与坐标、非负数的性质、动点问题,一元一次方程的应用,学会分类思想是解题的关键.
(1)先根据非负数的性质求得a,b, 则,,根据长方形的性质可求得点B的坐标.
(2)设点P移动的时间为t秒,点到轴的距离为个单位长度,则点P在边上或在边上,分别列方程求出t的值即可;
(3)分两种情况,当点P在边上时,则;当点P在边上时,则,分别求出,进一步即可得出点B的坐标.
【详解】(1)解:∵,
∴,,
∴,,
∴,,
∵四边形是长方形,
∴,
∴轴,轴,
∴
(2)设点P移动的时间为t秒,
∵点P到y轴的距离为4个单位长度,
∴点P在边上或在边上,
当点P在边长上,
则,
解得:,
当点P在边上,
则,
解得:.
(3)当点P在边上时,如下图:
∵,,
∴,
解得:,
∴点P的坐标为:
当点P在边上时,如下图:
∵,,
∴,
∴,
∴.
综上:否存在点P使的面积是12,此时,P点的坐标为或.
16.(1)(8,6)
(2)
(3)点Q的坐标为(3,0)或(-3,0).
【分析】(1)根据四边形ABCD是长方形,且D点与原点重合,点A在y轴上,点C在x轴上,AB=CD=8,AD=BC=6,可直接写出点B的坐标;
(2)由BP=8-3t,CQ=4t,列方程求出t的值即可;
(3)设点Q的坐标为(x,0),分两种情况讨论,一是点Q在线段CO上,则OQ=x,二是点Q在线段CO的延长线上,则OQ=-x,根据△ADQ的面积为9分别列方程求出相应的x的值即可.
【详解】(1)解:∵四边形ABCD是长方形,且D点与原点重合,点A在y轴上,点C在x轴上,AB=CD=8,AD=BC=6,
∴点B的坐标为(8,6),
故答案为:(8,6);
(2)解:根据题意,AP=3t,CQ=4t,
∴BP=8-3t,
∵BP=CQ,
∴8-3t=4t,
解得:t=;
故答案为:;
(3)解:设点Q的坐标为(x,0),
当点Q在线段CO上时,如图2,
∴OQ=x,
∵S△ADQ=AD OQ=9,
∴×6x=9,
解得x=3,
∴OQ=3,
∴Q(3,0);
当点Q在线段CO的延长线上,如图3,
∴OQ=-x,
∵S△ADQ=AD OQ=9,
∴×6(-x)=9,
解得x=-3,
∴OQ=3,
∴Q(-3,0),
综上所述,当点Q运动到距原点3个单位长度时,△ADQ的面积为9,此时点Q的坐标为(3,0)或(-3,0).
【点睛】此题考查了坐标与图形的性质,解题过程中还涉及数形结合、分类讨论等数学思想的运用,用含未知数的式子表示运动过程中线段的长是解题的关键.
17.(1)像一棵树;(2)x轴上的点有:,,,;y轴上的点有:;(3)点,,,在第一象限内,因为它们的横坐标与纵坐标都是正实数;点,在第四象限内,因为它们的横坐标是正实数,纵坐标是负实数;(4)点与的纵坐标相同,它们的连线段与x轴平行;点,,的横坐标相同,它们的连线段与y轴平行.
【分析】(1)依此描出各组点的坐标,然后依此连接,由图象可进行求解;
(2)根据图象可直接进行求解;
(3)根据平面直角坐标系中象限的符号特点可直接进行求解;
(4)根据图象可直接进行求解.
【详解】解:(1)描出各组点的坐标并依此连接,如图所示:
由图象可知:像一棵树;
(2)x轴上的点有:,,,;y轴上的点有:;
(3)点,,,在第一象限内,因为它们的横坐标与纵坐标都是正实数;点,在第四象限内,因为它们的横坐标是正实数,纵坐标是负实数;
(4)学生的发现可以多样.例如,点与的纵坐标相同,它们的连线段与x轴平行;点,,的横坐标相同,它们的连线段与y轴平行.
【点睛】本题主要考查平面直角坐标系,解题的关键是在平面直角坐标系中描出各点的坐标.
18.连接起来的图形像“房子”;(1)线段AG上的点都在x轴上,它们的纵坐标都等于0;线段AB上的点、线段CD与y轴的交点,它们都在y轴上,它们的横坐标都等于0;(2)线段EC平行于x轴,点E和点C的纵坐标相同.线段EC上其他点的纵坐标也相同,都是3;(3)点F和点G的横坐标相同.线段FG与y轴平行.
【分析】在坐标系中描出各点,再顺次连接可得一个房子的图案;
(1)结合图案分析,即可得出答案;
(2)结合图案分析,即可得出答案;
(3)结合图案分析,即可得出答案;
【详解】连接起来的图形像“房子”.
(1)线段AG上的点都在x轴上,它们的纵坐标都等于0;线段AB上的点、线段CD与y轴的交点,它们都在y轴上,它们的横坐标都等于0.
(2)线段EC平行于x轴,点E和点C的纵坐标相同.线段EC上其他点的纵坐标也相同,都是3.
(3)点F和点G的横坐标相同.线段FG与y轴平行.
【点睛】本题主要考查坐标与图形的性质,作图的关键是根据点的坐标确定点在平面直角坐标系中的位置,并根据位置依次连接,形成题目中要求的图形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
