华师大版七下(2024版)8.2多边形的内角和与外角和第2课时学案
文档属性
| 名称 | 华师大版七下(2024版)8.2多边形的内角和与外角和第2课时学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 359.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-03 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第8章三角形
8.2多边形的内角和与外角和第2课时
学习目标与重难点
学习目标:
1.理解并掌握多边形的外角和定理,且能够证明它.
2.能够综合应用多边形的内角和、外角和定理解决有关的问题.
3.经历多边形的外角和定理的探究过程,进一步体会转化的数学思想.
学习重点:多边形的外角和定理及其应用.
学习难点:能利用内角和与外角和定理解决实际问题.
预习自测
一、知识链接
1、n边形的内角和公式是什么?
它有什么作用呢?
自学自测
1.四边形外角和是( )
A. B. C. D.
2.一个七边形的内角和度数为( )
A.360° B.720° C.900° D.1080°
3.一个多边形的内角和是外角和的2倍,则这个多边形是几边形?( )
A.五角形 B.六边形 C.七边形 D.八边形
教学过程
一、创设情境、导入新课
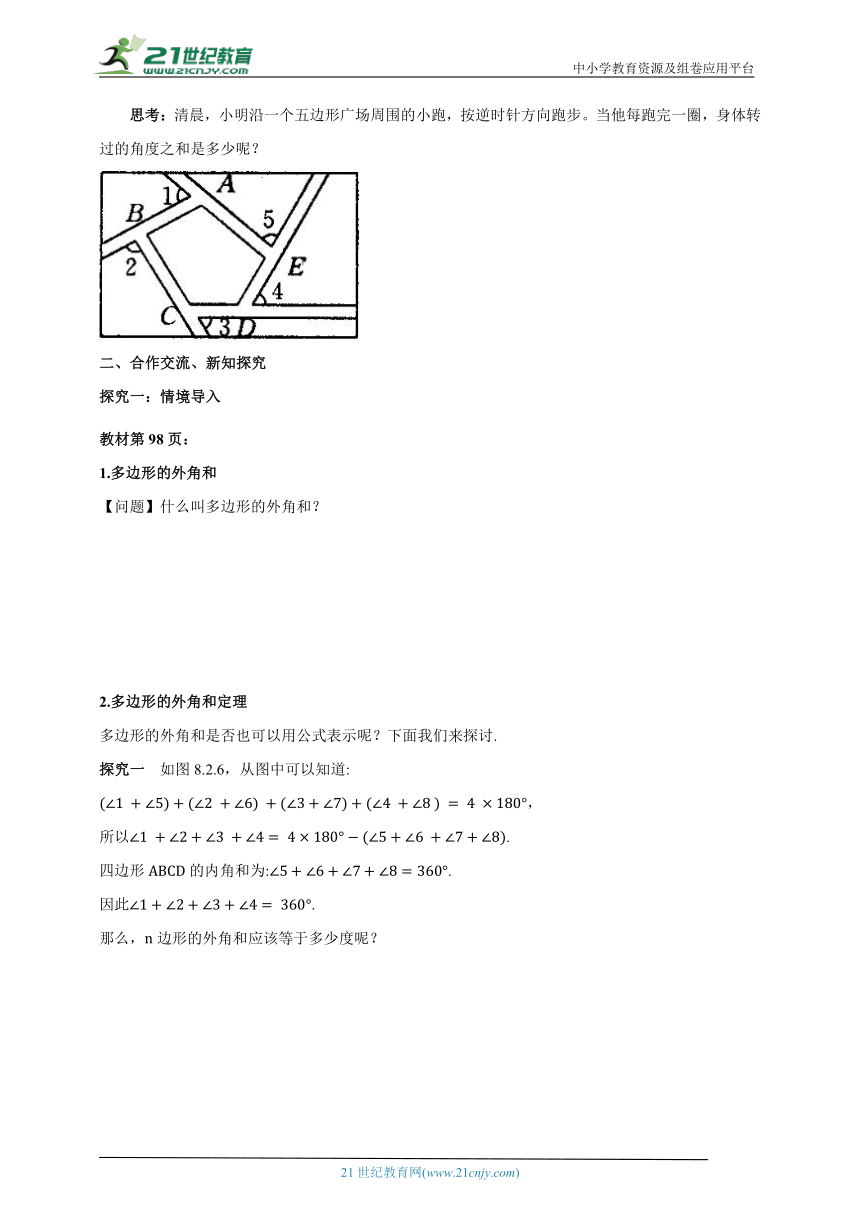
思考:清晨,小明沿一个五边形广场周围的小跑,按逆时针方向跑步。当他每跑完一圈,身体转过的角度之和是多少呢?
二、合作交流、新知探究
探究一:情境导入
教材第98页:
1.多边形的外角和
【问题】什么叫多边形的外角和?
2.多边形的外角和定理
多边形的外角和是否也可以用公式表示呢?下面我们来探讨.
探究一 如图8.2.6,从图中可以知道:
,
所以.
四边形的内角和为:.
因此.
那么,边形的外角和应该等于多少度呢?
探究二 根据边形的每一个内角与和它相邻的外角互为补角,就可以求得边形的外角和,据此,请将数据填入表中
探究三:例题讲解
教材第98页
例3 一个多边形的每个外角都是,这个多边形是几边形?
【问题探索】任何多边形的外角和都是,用外角和除以每个外角的度数即可得到边数.
【总结】此题主要考查了多边形的外角和,关键是掌握任何多边形的外角和都是360°.
例4 一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?
【问题探索】 多边形的内角和可以表示成,外角和是固定的360°,从而可根据一个多边形的内角和等于它的外角和的5倍列方程求解.
【总结】多边形的外角和与边数无关,都等于,本题考查多边形的内角和与外角和、方程的思想.关键是记住内角和的公式与外角和的特征.
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.若正多边形的一个外角是,则这个正多边形的边数是( )
A.4 B.5 C.6 D.7
2.当一个多边形的边数增加时,它的内角和与外角和的变化情况分别是( )
A.增大,增大 B.增大,不变
C.不变,增大 D.不变,不变
3.如图,五边形ABCDE的一个内角∠A110°,则∠1+∠2+∠3+∠4等于( )
A.360° B.290° C.270° D.250°
选做题:
4.如果一个正多边形的内角和是外角和的3倍,那么这个正多边形的边数为( )
A.5 B.6 C.7 D.8
5.一个多边形所有内角与外角的和为1 260°,则这个多边形的边数是( )
A.5 B.7 C.8 D.9
【综合拓展类作业】
6.一个正多边形的一个外角等于它的一个内角的,这个正多边形是几边形?
总结反思、拓展升华
【课堂总结】
知识点:1.多边形的外角:多边形内角的一边与另一边的反向延长线所组成的角.
2.多边形的外角和:在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
3.多边形的外角和等于360°.
注意事项:由于多边形的外角和等于360°,与边数无关,所以常把多边形内角的问题转化为外角和来处理.
五、【作业布置】
【知识技能类作业】
必做题:
1.正十二边形的外角和为( )
A.30° B.150° C.360° D.1 800°
2.已知一个多边形的每个外角都等于60°,则该多边形的边数是( )
A.4 B.5 C.6 D.7
3.若一个多边形的每个外角都等于36°,则这个多边形的边数为 .
4.如果一个多边形的内角和与外角和相等,那么这个多边形是( )
A.七边形 B.六边形 C.五边形 D.四边形
选做题:
5.佩佩在“黄娥古镇”研学时学习扎染技术,得到一个内角和为1 080°的正多边形图案,这个正多边形的每个外角为( )
A.36° B.40°
C.45° D.60°
6.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=67°,则∠AED的度数是( )
A.78°B.88°C.92°D.112°
7.一个多边形的内角和比它的外角和的2倍大180°,求这个多边形的边数.
【综合拓展类作业】
8.阅读下面的对话,解决问题:
(1)为什么说“一个多边形的内角和为2 020°”不可能?请计算说明.
(2)小明求的是 边形的内角和.
(3)错当成内角的那个外角为 度.
答案:
自学测试:
1.【答案】C
2.【答案】C
3.【答案】B
课堂巩固:
1.C 2.B 3.B 4.D 5.B
6.解:设外角为,则内角为,
由题意得,
解得.
.
作业布置:
1.C;2.C;3.10;4.D;
5.C;6.B;
7. 解:设这个多边形的边数为n,根据题意,得
(n-2)·180°=2×360°+180°,
解得n=7.
所以这个多边形的边数是7.
8.(1) 解:设这个多边形的边数为n,则
(n-2)·180°=2 020°,
解得n=13.
∵n为正整数,
∴一个多边形的内角和为2 020°是不可能.
(2)十三或十四
(3)110或20
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第8章三角形
8.2多边形的内角和与外角和第2课时
学习目标与重难点
学习目标:
1.理解并掌握多边形的外角和定理,且能够证明它.
2.能够综合应用多边形的内角和、外角和定理解决有关的问题.
3.经历多边形的外角和定理的探究过程,进一步体会转化的数学思想.
学习重点:多边形的外角和定理及其应用.
学习难点:能利用内角和与外角和定理解决实际问题.
预习自测
一、知识链接
1、n边形的内角和公式是什么?
它有什么作用呢?
自学自测
1.四边形外角和是( )
A. B. C. D.
2.一个七边形的内角和度数为( )
A.360° B.720° C.900° D.1080°
3.一个多边形的内角和是外角和的2倍,则这个多边形是几边形?( )
A.五角形 B.六边形 C.七边形 D.八边形
教学过程
一、创设情境、导入新课
思考:清晨,小明沿一个五边形广场周围的小跑,按逆时针方向跑步。当他每跑完一圈,身体转过的角度之和是多少呢?
二、合作交流、新知探究
探究一:情境导入
教材第98页:
1.多边形的外角和
【问题】什么叫多边形的外角和?
2.多边形的外角和定理
多边形的外角和是否也可以用公式表示呢?下面我们来探讨.
探究一 如图8.2.6,从图中可以知道:
,
所以.
四边形的内角和为:.
因此.
那么,边形的外角和应该等于多少度呢?
探究二 根据边形的每一个内角与和它相邻的外角互为补角,就可以求得边形的外角和,据此,请将数据填入表中
探究三:例题讲解
教材第98页
例3 一个多边形的每个外角都是,这个多边形是几边形?
【问题探索】任何多边形的外角和都是,用外角和除以每个外角的度数即可得到边数.
【总结】此题主要考查了多边形的外角和,关键是掌握任何多边形的外角和都是360°.
例4 一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?
【问题探索】 多边形的内角和可以表示成,外角和是固定的360°,从而可根据一个多边形的内角和等于它的外角和的5倍列方程求解.
【总结】多边形的外角和与边数无关,都等于,本题考查多边形的内角和与外角和、方程的思想.关键是记住内角和的公式与外角和的特征.
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.若正多边形的一个外角是,则这个正多边形的边数是( )
A.4 B.5 C.6 D.7
2.当一个多边形的边数增加时,它的内角和与外角和的变化情况分别是( )
A.增大,增大 B.增大,不变
C.不变,增大 D.不变,不变
3.如图,五边形ABCDE的一个内角∠A110°,则∠1+∠2+∠3+∠4等于( )
A.360° B.290° C.270° D.250°
选做题:
4.如果一个正多边形的内角和是外角和的3倍,那么这个正多边形的边数为( )
A.5 B.6 C.7 D.8
5.一个多边形所有内角与外角的和为1 260°,则这个多边形的边数是( )
A.5 B.7 C.8 D.9
【综合拓展类作业】
6.一个正多边形的一个外角等于它的一个内角的,这个正多边形是几边形?
总结反思、拓展升华
【课堂总结】
知识点:1.多边形的外角:多边形内角的一边与另一边的反向延长线所组成的角.
2.多边形的外角和:在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
3.多边形的外角和等于360°.
注意事项:由于多边形的外角和等于360°,与边数无关,所以常把多边形内角的问题转化为外角和来处理.
五、【作业布置】
【知识技能类作业】
必做题:
1.正十二边形的外角和为( )
A.30° B.150° C.360° D.1 800°
2.已知一个多边形的每个外角都等于60°,则该多边形的边数是( )
A.4 B.5 C.6 D.7
3.若一个多边形的每个外角都等于36°,则这个多边形的边数为 .
4.如果一个多边形的内角和与外角和相等,那么这个多边形是( )
A.七边形 B.六边形 C.五边形 D.四边形
选做题:
5.佩佩在“黄娥古镇”研学时学习扎染技术,得到一个内角和为1 080°的正多边形图案,这个正多边形的每个外角为( )
A.36° B.40°
C.45° D.60°
6.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=67°,则∠AED的度数是( )
A.78°B.88°C.92°D.112°
7.一个多边形的内角和比它的外角和的2倍大180°,求这个多边形的边数.
【综合拓展类作业】
8.阅读下面的对话,解决问题:
(1)为什么说“一个多边形的内角和为2 020°”不可能?请计算说明.
(2)小明求的是 边形的内角和.
(3)错当成内角的那个外角为 度.
答案:
自学测试:
1.【答案】C
2.【答案】C
3.【答案】B
课堂巩固:
1.C 2.B 3.B 4.D 5.B
6.解:设外角为,则内角为,
由题意得,
解得.
.
作业布置:
1.C;2.C;3.10;4.D;
5.C;6.B;
7. 解:设这个多边形的边数为n,根据题意,得
(n-2)·180°=2×360°+180°,
解得n=7.
所以这个多边形的边数是7.
8.(1) 解:设这个多边形的边数为n,则
(n-2)·180°=2 020°,
解得n=13.
∵n为正整数,
∴一个多边形的内角和为2 020°是不可能.
(2)十三或十四
(3)110或20
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
