3.3.2 一元一次不等式的解法 课件(共20张PPT)
文档属性
| 名称 | 3.3.2 一元一次不等式的解法 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 459.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 04:55:59 | ||
图片预览







文档简介
(共20张PPT)
一元一次不等式的解法
七年级下册 第三章 3.3.2
学习目标
1.学会解含分母的一元一次不等式的方法,能够熟练地通过去分母、去括号、移项、合并同类项、系数化为1等步骤求解不等式。
2.能够准确地在数轴上表示不等式的解集。
3.通过类比一元一次方程的解法,自主探究含分母的一元一次不等式的解法,培养的类比思维和自主学习能力。
复习回顾
1. 去括号(乘法对加法的分配律)
2.移项(不等式的基本性质1)
3.合并同类项
4.化系数为1(不等式的基本性质2或3)
解不含分母的一元一次不等式的一般步骤
注意:运用不等式的基本性质3时记得变号
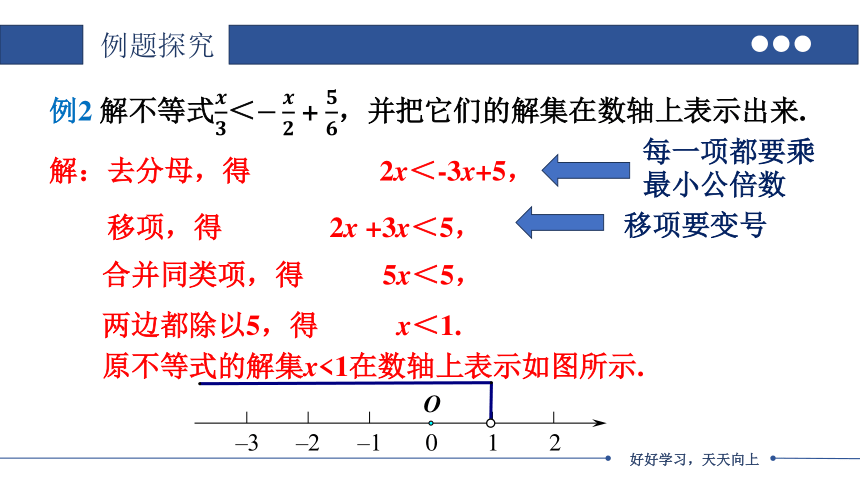
例2 解不等式< + ,并把它们的解集在数轴上表示出来.
例题探究
解:去分母,得 2x<-3x+5,
移项,得 2x +3x<5,
合并同类项,得 5x<5,
两边都除以5,得 x<1.
每一项都要乘最小公倍数
原不等式的解集x<1在数轴上表示如图所示.
移项要变号
例3 解不等式+1<,并把它们的解集在数轴上表示出来.
例题探究
去括号,得2x-10+6≤9x,
解:去分母,得2(x-5)+6≤9x,
移项,得2x - 9x≤10 - 6,
合并同类项,-7x≤4,
两边都除以 -7,得x≥.
原不等式的解集x≥在数轴上表示如图所示.
例题探究
一元一次不等式与解一元一次方程的解法有什么哪些类似之处?有哪些不同之处?与同学交流你的认识.
议一议
一元一次不等式与一元一次方程的一般解法都是:去分母、去括号、移项、合并同类项、系数化为1.
不同的是系数化为1时,方程的两边都乘(或除以)同一个数,等式仍成立;不等式的两边都乘(或除以)同一个正数,不等号的方向不变.不等式的两边都乘(或除以)同一个负数,不等号的方教材向改变.
例题探究
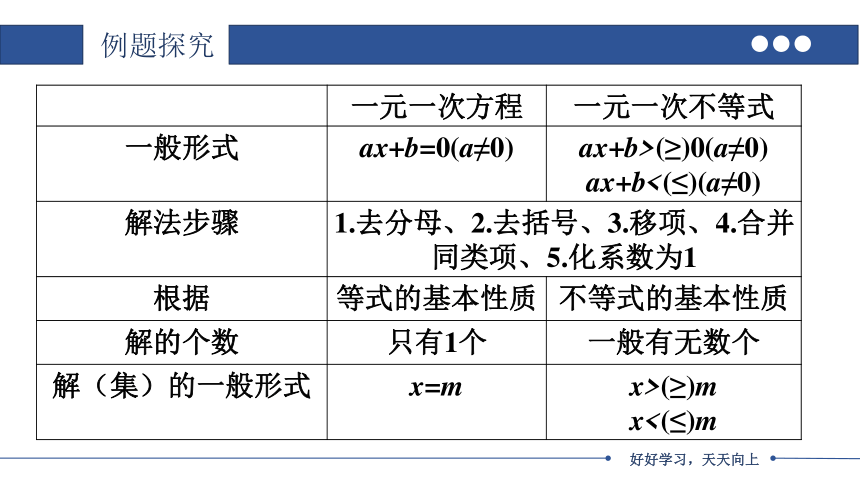
一元一次方程 一元一次不等式
一般形式 ax+b=0(a≠0) ax+b>(≥)0(a≠0)
ax+b<(≤)(a≠0)
解法步骤 1.去分母、2.去括号、3.移项、4.合并同类项、5.化系数为1
根据 等式的基本性质 不等式的基本性质
解的个数 只有1个 一般有无数个
解(集)的一般形式 x=m x>(≥)m
x<(≤)m
例4 将x用哪些实数代入,代数式x+2的值大于或等于0?其中满足条件的正整数有哪些?
例题探究
解:由题意可知,需先求不等式x+2≥0的解集.
移项,得x≥2,
两边都乘3,得 x ≤6.
结合题意可知,满足条件的正整数有 1,2,3,4,5,6.
课堂小结
1.去分母(不等式的基本性质2或3)
2.去括号(乘法对加法的分配律)
3.移项(不等式的基本性质1)
4.合并同类项
5.化系数为1(不等式的基本性质2或3)
解含分母的一元一次不等式的一般步骤
注意:运用不等式的基本性质3时记得变号
课堂练习
1.将不等式->1去分母正确的是 ( )
A. 2(x-1)-x-2>1
B. 2(x-1)-x+2>1
C. 2(x-1)-x-2>4
D. 2(x-1)-(x-2)>4
D
2.如图,点 M、N在数轴上分别表示数 x-12、-x+1,则x的值不能是( )
A.1
B.0
C.-2
D.-1
课堂练习
A
3.不等式<1的正整数解有( )个.
A.2
B.3
C.4
D.5
课堂练习
B
4.已知不等式-(x-1)≤3-x的最大整数解是方程3x-m=7的解,则实数m的值是 ( )
A. 8
B. -8
C. 22
D. 4
课堂练习
A
5.已知整式的值为P. 若P的范围如图,则m的负整数值为________.
课堂练习
-3、-2、-1
6.解下列不等式,并把它们的解集在数轴上表示出来.
(1) >0; (2)≤ 1.
课堂练习
解:(1)去分母,得2(2x-1)-(5x-3)>0,
去括号,得4x-2-5x+3>0,
移项,得4x-5x>2-3,
合并同类项,得-x>-1,
两边都除以-1,得x<1.
原不等式的解集x<1在数轴上的表示如图.
6.解下列不等式,并把它们的解集在数轴上表示出来.
(1) >0; (2)≤ 1.
课堂练习
解:(2)去分母,得4(2x-1)≤3(3x+2)-12,
去括号,得8x-4≤9x+6-12,
移项,得8x-9x≤6-12+4,
合并同类项,得-x≤-2,
两边都除以-1,得x≥2.
原不等式的解集x≥2在数轴上的表示如图.
7.将x 用哪些实数代入,能够使得多项式 - 的值不小于多项式的值?其中满足条件的正整数有哪些?
课堂练习
解:由题意可知,需先求不等式 - ≥ 的解集.
去分母,得4 (x+ 1)- 3(2 x- 1)≥ 2 (x- 3).
去括号,得4 x+ 4 - 6 x+ 3 ≥ 2 x- 6 .
移项,得4 x- 6 x- 2 x ≥ - 6 - 4 - 3 .
合并同类项,得- 4 x ≥ - 1 3 .
7.将x 用哪些实数代入,能够使得多项式 - 的值不小于多项式的值?其中满足条件的正整数有哪些?
课堂练习
两边都除以- 4 ,得x ≤ .
因此,当x 用小于或等于的实数代入时,都能使得多项式 - 的值不小于多项式的值,其中满足条件的正整数有1,2,3.
课后作业
课堂作业:P69 T1
家庭作业:《学法》P45 A组(基础一般)
B组(基础较好)
C组(选做)
一元一次不等式的解法
七年级下册 第三章 3.3.2
学习目标
1.学会解含分母的一元一次不等式的方法,能够熟练地通过去分母、去括号、移项、合并同类项、系数化为1等步骤求解不等式。
2.能够准确地在数轴上表示不等式的解集。
3.通过类比一元一次方程的解法,自主探究含分母的一元一次不等式的解法,培养的类比思维和自主学习能力。
复习回顾
1. 去括号(乘法对加法的分配律)
2.移项(不等式的基本性质1)
3.合并同类项
4.化系数为1(不等式的基本性质2或3)
解不含分母的一元一次不等式的一般步骤
注意:运用不等式的基本性质3时记得变号
例2 解不等式< + ,并把它们的解集在数轴上表示出来.
例题探究
解:去分母,得 2x<-3x+5,
移项,得 2x +3x<5,
合并同类项,得 5x<5,
两边都除以5,得 x<1.
每一项都要乘最小公倍数
原不等式的解集x<1在数轴上表示如图所示.
移项要变号
例3 解不等式+1<,并把它们的解集在数轴上表示出来.
例题探究
去括号,得2x-10+6≤9x,
解:去分母,得2(x-5)+6≤9x,
移项,得2x - 9x≤10 - 6,
合并同类项,-7x≤4,
两边都除以 -7,得x≥.
原不等式的解集x≥在数轴上表示如图所示.
例题探究
一元一次不等式与解一元一次方程的解法有什么哪些类似之处?有哪些不同之处?与同学交流你的认识.
议一议
一元一次不等式与一元一次方程的一般解法都是:去分母、去括号、移项、合并同类项、系数化为1.
不同的是系数化为1时,方程的两边都乘(或除以)同一个数,等式仍成立;不等式的两边都乘(或除以)同一个正数,不等号的方向不变.不等式的两边都乘(或除以)同一个负数,不等号的方教材向改变.
例题探究
一元一次方程 一元一次不等式
一般形式 ax+b=0(a≠0) ax+b>(≥)0(a≠0)
ax+b<(≤)(a≠0)
解法步骤 1.去分母、2.去括号、3.移项、4.合并同类项、5.化系数为1
根据 等式的基本性质 不等式的基本性质
解的个数 只有1个 一般有无数个
解(集)的一般形式 x=m x>(≥)m
x<(≤)m
例4 将x用哪些实数代入,代数式x+2的值大于或等于0?其中满足条件的正整数有哪些?
例题探究
解:由题意可知,需先求不等式x+2≥0的解集.
移项,得x≥2,
两边都乘3,得 x ≤6.
结合题意可知,满足条件的正整数有 1,2,3,4,5,6.
课堂小结
1.去分母(不等式的基本性质2或3)
2.去括号(乘法对加法的分配律)
3.移项(不等式的基本性质1)
4.合并同类项
5.化系数为1(不等式的基本性质2或3)
解含分母的一元一次不等式的一般步骤
注意:运用不等式的基本性质3时记得变号
课堂练习
1.将不等式->1去分母正确的是 ( )
A. 2(x-1)-x-2>1
B. 2(x-1)-x+2>1
C. 2(x-1)-x-2>4
D. 2(x-1)-(x-2)>4
D
2.如图,点 M、N在数轴上分别表示数 x-12、-x+1,则x的值不能是( )
A.1
B.0
C.-2
D.-1
课堂练习
A
3.不等式<1的正整数解有( )个.
A.2
B.3
C.4
D.5
课堂练习
B
4.已知不等式-(x-1)≤3-x的最大整数解是方程3x-m=7的解,则实数m的值是 ( )
A. 8
B. -8
C. 22
D. 4
课堂练习
A
5.已知整式的值为P. 若P的范围如图,则m的负整数值为________.
课堂练习
-3、-2、-1
6.解下列不等式,并把它们的解集在数轴上表示出来.
(1) >0; (2)≤ 1.
课堂练习
解:(1)去分母,得2(2x-1)-(5x-3)>0,
去括号,得4x-2-5x+3>0,
移项,得4x-5x>2-3,
合并同类项,得-x>-1,
两边都除以-1,得x<1.
原不等式的解集x<1在数轴上的表示如图.
6.解下列不等式,并把它们的解集在数轴上表示出来.
(1) >0; (2)≤ 1.
课堂练习
解:(2)去分母,得4(2x-1)≤3(3x+2)-12,
去括号,得8x-4≤9x+6-12,
移项,得8x-9x≤6-12+4,
合并同类项,得-x≤-2,
两边都除以-1,得x≥2.
原不等式的解集x≥2在数轴上的表示如图.
7.将x 用哪些实数代入,能够使得多项式 - 的值不小于多项式的值?其中满足条件的正整数有哪些?
课堂练习
解:由题意可知,需先求不等式 - ≥ 的解集.
去分母,得4 (x+ 1)- 3(2 x- 1)≥ 2 (x- 3).
去括号,得4 x+ 4 - 6 x+ 3 ≥ 2 x- 6 .
移项,得4 x- 6 x- 2 x ≥ - 6 - 4 - 3 .
合并同类项,得- 4 x ≥ - 1 3 .
7.将x 用哪些实数代入,能够使得多项式 - 的值不小于多项式的值?其中满足条件的正整数有哪些?
课堂练习
两边都除以- 4 ,得x ≤ .
因此,当x 用小于或等于的实数代入时,都能使得多项式 - 的值不小于多项式的值,其中满足条件的正整数有1,2,3.
课后作业
课堂作业:P69 T1
家庭作业:《学法》P45 A组(基础一般)
B组(基础较好)
C组(选做)
同课章节目录
