第二十章 数据的分析 能力提优测试卷(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第二十章 数据的分析 能力提优测试卷(含答案) 2024-2025学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 104.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:20:24 | ||
图片预览


文档简介
第二十章 数据的分析
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.第三届“红色日记”征文大赛的征文内容分为“不忘初心”和“红色传承”两部分.其中五位评委给参赛者小亮的征文评分分别为88,92,90,95,90,则这组数据的中位数是 ( )
A.88 B.90 C.92 D.93
2.根据PM2.5空气质量标准:24小时PM2.5均值在0~35(微克/米3)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表,则这组PM2.5数据的众数是 ( )
天数 3 1 1 1 1
PM2.5 18 20 21 29 30
A.21微克/米3 B.20微克/米3
C.19微克/米3 D.18微克/米3
3.若6名学生的体重(单位:kg)分别是42,43,45,47,47,52,则这6名学生的平均体重是 ( )
A.44 kg B.45 kg C.46 kg D.47 kg
4.灾害无情人有情,爱心捐款传真情.在抢险救灾工作期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额∕元 5 10 20 50 100
人数 4 16 15 10 5
则他们的捐款金额的平均数、中位数分别是 ( )
A.29.6,10 B.39,20 C.39,10 D.29.6,20
5.为了了解某公司员工的年工资情况,小明随机调查了10位员工,其年工资(单位:万元)分别为2.8,3,3,4,5,5,6,7,10,20.下列统计量中,能合理反映该公司工资中等水平的是 ( )
A.平均数 B.中位数 C.众数 D.方差
6.某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差s2=39.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是 ( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
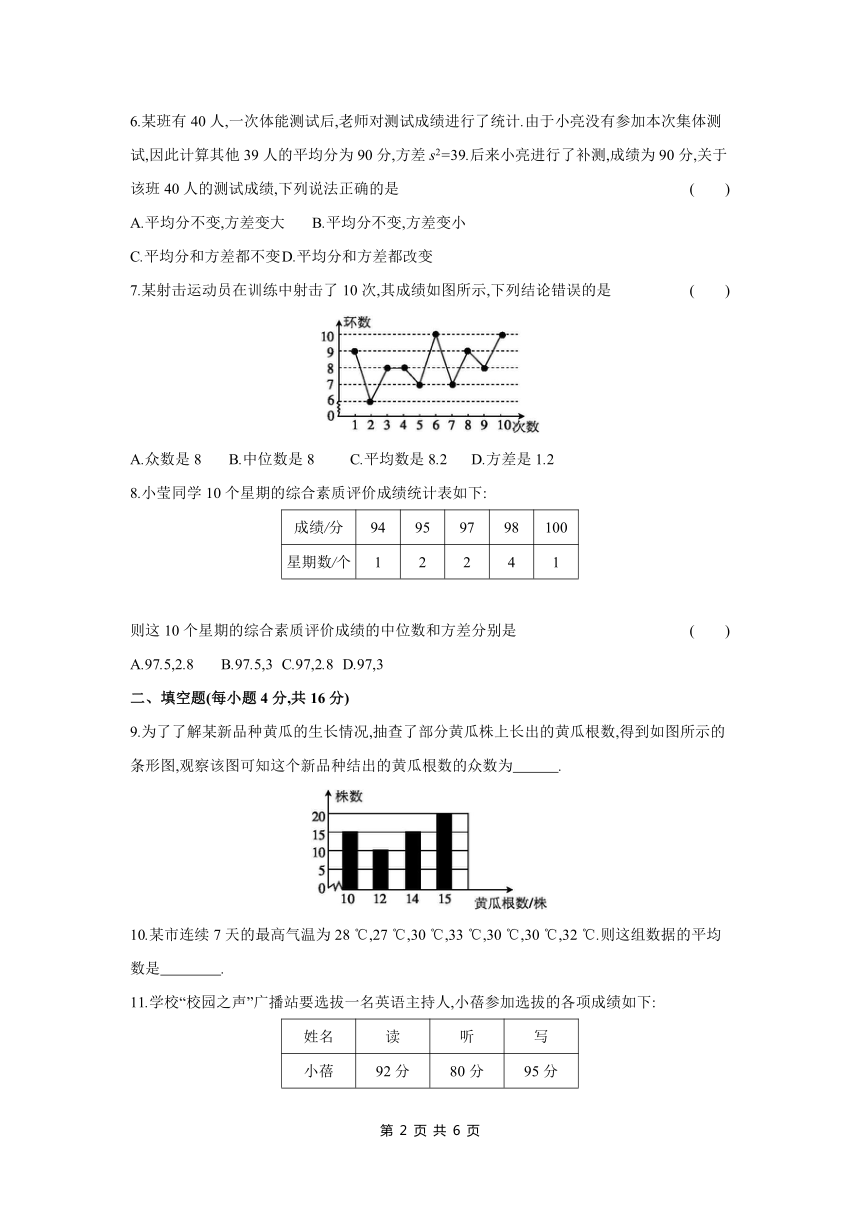
7.某射击运动员在训练中射击了10次,其成绩如图所示,下列结论错误的是 ( )
A.众数是8 B.中位数是8 C.平均数是8.2 D.方差是1.2
8.小莹同学10个星期的综合素质评价成绩统计表如下:
成绩/分 94 95 97 98 100
星期数/个 1 2 2 4 1
则这10个星期的综合素质评价成绩的中位数和方差分别是 ( )
A.97.5,2.8 B.97.5,3 C.97,2.8 D.97,3
二、填空题(每小题4分,共16分)
9.为了了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到如图所示的条形图,观察该图可知这个新品种结出的黄瓜根数的众数为 .
10.某市连续7天的最高气温为28 ℃,27 ℃,30 ℃,33 ℃,30 ℃,30 ℃,32 ℃.则这组数据的平均数是 .
11.学校“校园之声”广播站要选拔一名英语主持人,小蓓参加选拔的各项成绩如下:
姓名 读 听 写
小蓓 92分 80分 95分
若把读、听、写的成绩按5∶3∶2的比例记入个人的总分,则小蓓的个人总分为 分.
12.已知一组数据92,94,98,91,95的中位数为a,方差为b,则a+b= .
三、解答题(本大题共4小题,共52分)
13.(10分)黄磊参加班长竞选,需要进行演讲、学生代表评分、答辩三个环节,其中学生代表评分项的得分以六位代表评分的平均数计分,他的各项得分如表所示:
竞评项目 演讲 学生代表评分 答辩
得分 9.5 9.3 9.3 9.0 9.4 9.4 9.4 9.2
(1)求学生代表给黄磊评分的众数和中位数;
(2)根据竞选规则,将演讲、学生代表评分、答辩的得分按20%,50%,30%的比例计算成绩,求黄磊的最后得分.
14.(12分)甲、乙两人加工同一种直径为100 mm的零件,现从他们加工好的零件中随机各抽取6个,量得它们的直径(单位: mm)如下:
甲:98,102,100,100,101,99.
乙:100,103,101,97,100,99.
(1)分别求出上述两组数据的平均数和方差;
(2)结合(1)中的统计数据,请你评价两人的加工质量.
15.(14分)某车间有20名工人,某天他们生产的零件个数统计如下表:
生产零件的个数/个 9 10 11 12 13 15 16 19 20
工人人数/人 1 1 6 4 2 2 2 1 1
(1)求这一天20名工人生产零件的平均个数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”
16.(16分)在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m)绘制出如下统计图1和2,请根据相关信息,解答下列问题:
(1)图1中a的值为 ;
(2)求统计的这组初赛成绩的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65 m的运动员能否进入复赛.(不必说明理由)
参考答案
一、选择题
1 2 3 4 5 6 7 8
B D C D B B D B
3.C 【解析】平均体重为×(42+43+45+47×2+52)=46(kg).
4.D 【解析】平均数为×(5×4+10×16+20×15+50×10+100×5)=29.6(元),总共有50人捐款,其中第25,26位学生的捐款金额都是20元,即中位数为20元.
5.B 【解析】中位数反映的是一组数据的中等水平,表示比它多的有一半,比它少的有一半.
6.B 【解析】其他39人的平均分为90分,补测的小亮也是90分,因此40人的平均分为90分,不变;方差变为<39,变小了.
7.D 【解析】运动员10次射击的成绩依次是9,6,8,8,7,10,7,9,8,10,其中8出现的次数最多,故众数是8,A正确;按顺序排列为6,7,7,8,8,8,9,9,10,10,中间两个数是8和8,故中位数为8,B正确;平均数为8.2,C正确;方差为1.56,D错误.
8.B 【解析】成绩总共10个数,按从小到大排序后中间两个数为97和98,故中位数为97.5;这10个数的平均数==97,故其方差为s2=×[(94-97)2+(95-97)2×2+(97-97)2+(98-97)2×4+(100-97)2]=3.
二、填空题
9 10 11 12
15 30 ℃ 89 100
11.89 【解析】=89.
12.100 【解析】中位数a=94,平均数为=94,所以方差b=×[(92-94)2+(94-94)2+(98-94)2+(91-94)2+(95-94)2]=6,所以a+b=94+6=100.
三、解答题
13.解:(1)将学生代表评分按从小到大顺序排列为9.0,9.3,9.3,9.4,9.4,9.4,所以中位数为×(9.3+9.4)=9.35(分),众数为9.4分. (4分)
(2)学生代表的平均分为×(9.3×2+9.0+9.4×3)=9.3(7分), (7分)
所以黄磊的最后得分为9.5×20%+9.3×50%+9.2×30%=1.9+4.65+2.76=9.31(分). (10分)
14.解:(1)=
=100(mm),
=×[(98-100)2+(102-100)2+2×(100-100)2+(101-100)2+(99-100)2]=;
(4分)
==100(mm),
=×[2×(100-100)2+(103-100)2+(101-100)2+(97-100)2+(99-100)2]=. (8分)
(2)甲、乙两组数据的平均数都等于标准值,但甲的方差比乙的方差小,所以甲的质量更好. (12分)
15.解:(1)=×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)=13(个).
答:这一天20名工人生产零件的平均个数为13. (6分)
(2)中位数为12个,众数为11个.
当定额为13个时,有8人达标,6人获奖,不利于提高工人的积极性;
当定额为12个时,有12人达标,8人获奖,不利于提高大多数工人的积极性;
当定额为11个时,有18人达标,12人获奖,有利于提高大多数工人的积极性.
所以定额为11个. (14分)
16.解:(1)25 (4分)
(2)平均数为=
=1.61(m), (8分)
因为在这组数据中,1.65 m出现了6次,次数最多,所以这组数据的众数为1.65 m; (10分)
将这组数据从小到大排列,其中处于中间的两个数都是1.60 m,所以中位数为1.60 m. (14分)
(3)能. (16分)
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.第三届“红色日记”征文大赛的征文内容分为“不忘初心”和“红色传承”两部分.其中五位评委给参赛者小亮的征文评分分别为88,92,90,95,90,则这组数据的中位数是 ( )
A.88 B.90 C.92 D.93
2.根据PM2.5空气质量标准:24小时PM2.5均值在0~35(微克/米3)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表,则这组PM2.5数据的众数是 ( )
天数 3 1 1 1 1
PM2.5 18 20 21 29 30
A.21微克/米3 B.20微克/米3
C.19微克/米3 D.18微克/米3
3.若6名学生的体重(单位:kg)分别是42,43,45,47,47,52,则这6名学生的平均体重是 ( )
A.44 kg B.45 kg C.46 kg D.47 kg
4.灾害无情人有情,爱心捐款传真情.在抢险救灾工作期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额∕元 5 10 20 50 100
人数 4 16 15 10 5
则他们的捐款金额的平均数、中位数分别是 ( )
A.29.6,10 B.39,20 C.39,10 D.29.6,20
5.为了了解某公司员工的年工资情况,小明随机调查了10位员工,其年工资(单位:万元)分别为2.8,3,3,4,5,5,6,7,10,20.下列统计量中,能合理反映该公司工资中等水平的是 ( )
A.平均数 B.中位数 C.众数 D.方差
6.某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差s2=39.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是 ( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
7.某射击运动员在训练中射击了10次,其成绩如图所示,下列结论错误的是 ( )
A.众数是8 B.中位数是8 C.平均数是8.2 D.方差是1.2
8.小莹同学10个星期的综合素质评价成绩统计表如下:
成绩/分 94 95 97 98 100
星期数/个 1 2 2 4 1
则这10个星期的综合素质评价成绩的中位数和方差分别是 ( )
A.97.5,2.8 B.97.5,3 C.97,2.8 D.97,3
二、填空题(每小题4分,共16分)
9.为了了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到如图所示的条形图,观察该图可知这个新品种结出的黄瓜根数的众数为 .
10.某市连续7天的最高气温为28 ℃,27 ℃,30 ℃,33 ℃,30 ℃,30 ℃,32 ℃.则这组数据的平均数是 .
11.学校“校园之声”广播站要选拔一名英语主持人,小蓓参加选拔的各项成绩如下:
姓名 读 听 写
小蓓 92分 80分 95分
若把读、听、写的成绩按5∶3∶2的比例记入个人的总分,则小蓓的个人总分为 分.
12.已知一组数据92,94,98,91,95的中位数为a,方差为b,则a+b= .
三、解答题(本大题共4小题,共52分)
13.(10分)黄磊参加班长竞选,需要进行演讲、学生代表评分、答辩三个环节,其中学生代表评分项的得分以六位代表评分的平均数计分,他的各项得分如表所示:
竞评项目 演讲 学生代表评分 答辩
得分 9.5 9.3 9.3 9.0 9.4 9.4 9.4 9.2
(1)求学生代表给黄磊评分的众数和中位数;
(2)根据竞选规则,将演讲、学生代表评分、答辩的得分按20%,50%,30%的比例计算成绩,求黄磊的最后得分.
14.(12分)甲、乙两人加工同一种直径为100 mm的零件,现从他们加工好的零件中随机各抽取6个,量得它们的直径(单位: mm)如下:
甲:98,102,100,100,101,99.
乙:100,103,101,97,100,99.
(1)分别求出上述两组数据的平均数和方差;
(2)结合(1)中的统计数据,请你评价两人的加工质量.
15.(14分)某车间有20名工人,某天他们生产的零件个数统计如下表:
生产零件的个数/个 9 10 11 12 13 15 16 19 20
工人人数/人 1 1 6 4 2 2 2 1 1
(1)求这一天20名工人生产零件的平均个数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”
16.(16分)在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m)绘制出如下统计图1和2,请根据相关信息,解答下列问题:
(1)图1中a的值为 ;
(2)求统计的这组初赛成绩的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65 m的运动员能否进入复赛.(不必说明理由)
参考答案
一、选择题
1 2 3 4 5 6 7 8
B D C D B B D B
3.C 【解析】平均体重为×(42+43+45+47×2+52)=46(kg).
4.D 【解析】平均数为×(5×4+10×16+20×15+50×10+100×5)=29.6(元),总共有50人捐款,其中第25,26位学生的捐款金额都是20元,即中位数为20元.
5.B 【解析】中位数反映的是一组数据的中等水平,表示比它多的有一半,比它少的有一半.
6.B 【解析】其他39人的平均分为90分,补测的小亮也是90分,因此40人的平均分为90分,不变;方差变为<39,变小了.
7.D 【解析】运动员10次射击的成绩依次是9,6,8,8,7,10,7,9,8,10,其中8出现的次数最多,故众数是8,A正确;按顺序排列为6,7,7,8,8,8,9,9,10,10,中间两个数是8和8,故中位数为8,B正确;平均数为8.2,C正确;方差为1.56,D错误.
8.B 【解析】成绩总共10个数,按从小到大排序后中间两个数为97和98,故中位数为97.5;这10个数的平均数==97,故其方差为s2=×[(94-97)2+(95-97)2×2+(97-97)2+(98-97)2×4+(100-97)2]=3.
二、填空题
9 10 11 12
15 30 ℃ 89 100
11.89 【解析】=89.
12.100 【解析】中位数a=94,平均数为=94,所以方差b=×[(92-94)2+(94-94)2+(98-94)2+(91-94)2+(95-94)2]=6,所以a+b=94+6=100.
三、解答题
13.解:(1)将学生代表评分按从小到大顺序排列为9.0,9.3,9.3,9.4,9.4,9.4,所以中位数为×(9.3+9.4)=9.35(分),众数为9.4分. (4分)
(2)学生代表的平均分为×(9.3×2+9.0+9.4×3)=9.3(7分), (7分)
所以黄磊的最后得分为9.5×20%+9.3×50%+9.2×30%=1.9+4.65+2.76=9.31(分). (10分)
14.解:(1)=
=100(mm),
=×[(98-100)2+(102-100)2+2×(100-100)2+(101-100)2+(99-100)2]=;
(4分)
==100(mm),
=×[2×(100-100)2+(103-100)2+(101-100)2+(97-100)2+(99-100)2]=. (8分)
(2)甲、乙两组数据的平均数都等于标准值,但甲的方差比乙的方差小,所以甲的质量更好. (12分)
15.解:(1)=×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)=13(个).
答:这一天20名工人生产零件的平均个数为13. (6分)
(2)中位数为12个,众数为11个.
当定额为13个时,有8人达标,6人获奖,不利于提高工人的积极性;
当定额为12个时,有12人达标,8人获奖,不利于提高大多数工人的积极性;
当定额为11个时,有18人达标,12人获奖,有利于提高大多数工人的积极性.
所以定额为11个. (14分)
16.解:(1)25 (4分)
(2)平均数为=
=1.61(m), (8分)
因为在这组数据中,1.65 m出现了6次,次数最多,所以这组数据的众数为1.65 m; (10分)
将这组数据从小到大排列,其中处于中间的两个数都是1.60 m,所以中位数为1.60 m. (14分)
(3)能. (16分)
