第十八章 平行四边形 基础过关测试卷(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十八章 平行四边形 基础过关测试卷(含答案) 2024-2025学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览



文档简介
第十八章 平行四边形
基础过关测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.在 ABCD中,AB=3 cm,BC=5 cm,则 ABCD的周长是 ( )
A.8 cm B.14 cm C.15 cm D.16 cm
2.在 ABCD中,对角线AC,BD相交于点O,如果能够判定 ABCD为矩形,那么还需添加的条件是 ( )
A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD
3.如图,在△ABC中,D,E分别是AB,AC的中点,如果DE=3,那么BC的长为 ( )
A.4 B.5 C.6 D.7
4.如图,直线a∥b,CD⊥直线b,则直线a,b之间的距离是 ( )
A.线段AB的长度 B.线段GH的长度
C.线段EF的长度 D.线段CD的长度
5.如图,在△ABC中,∠ACB=90°,AB=10,D是AB的中点,则CD= ( )
A.4 B.5 C.6 D.8
6.如图,菱形ABCD的顶点C在直线MN上,若∠1=55°,∠2=15°,则∠ABD的度数为 ( )
A.20° B.35° C.40° D.50°
7.如图,矩形ABCD和矩形BDEF,点A在EF边上,设矩形ABCD和矩形BDEF的面积分别为S1,S2,则S1与S2的大小关系为 ( )
A.S1=S2 B.S1>S2 C.S18.如图,正方形ABCD的边长为2,E是BC的中点,DF⊥AE,交AB于点F,则DF的长为 ( )
A. B. C.2 D.3
二、填空题(每小题4分,共16分)
9.在四边形ABCD中,∠A+∠B=180°,添加条件 (填一个即可),则可使四边形ABCD成为平行四边形.
10.如图,在矩形ABCD中,对角线AC,BD相交于点O,如果∠ADO=75°,那么∠COD的度数是 .
11.菱形ABCD的边长为13 cm,其中对角线BD长10 cm,则菱形ABCD的面积为 cm2.
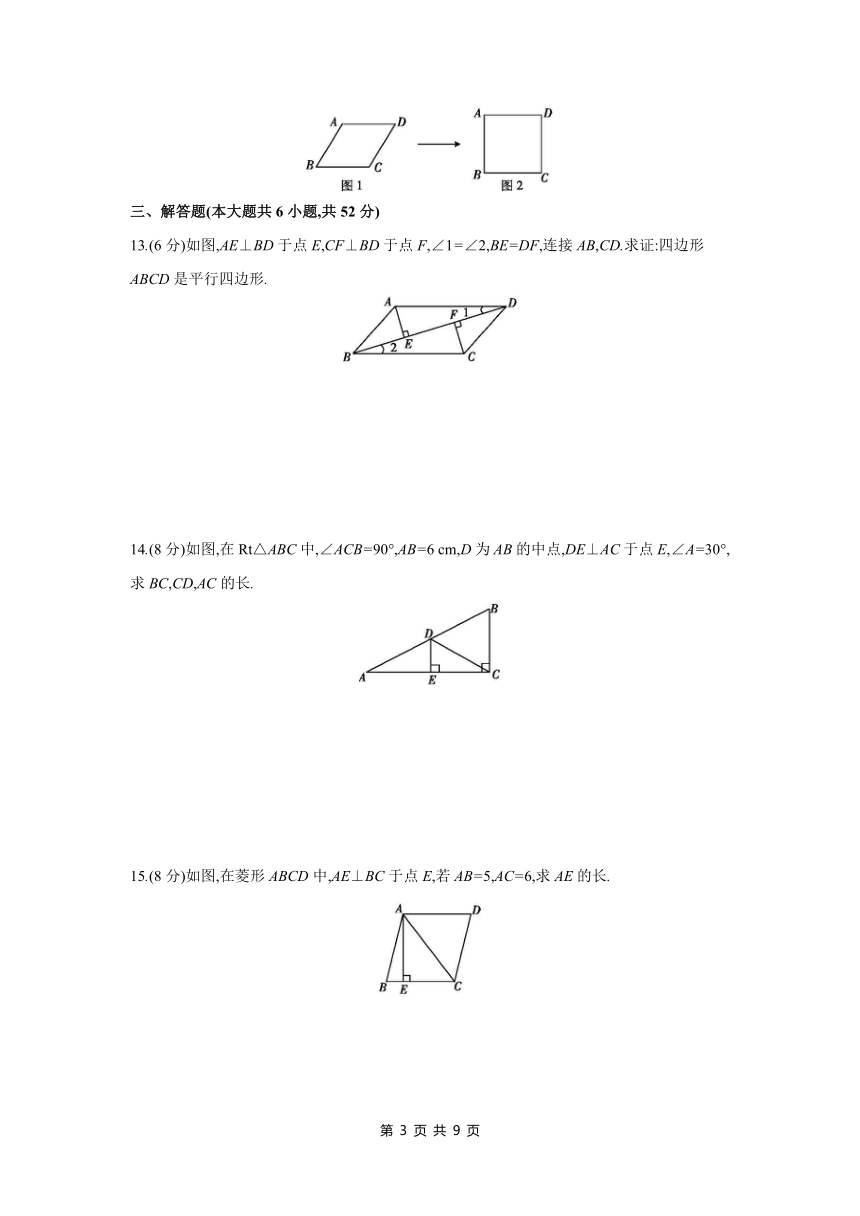
12.小明用四根长度相同的木条制作了能够活动的菱形学具,他先把活动学具制作成为图1所示的菱形,并测得∠B=60°,接着把活动学具制作成为图2所示的正方形,并测得正方形的对角线AC=40 cm,则图1中对角线AC的长为 cm.
三、解答题(本大题共6小题,共52分)
13.(6分)如图,AE⊥BD于点E,CF⊥BD于点F,∠1=∠2,BE=DF,连接AB,CD.求证:四边形ABCD是平行四边形.
14.(8分)如图,在Rt△ABC中,∠ACB=90°,AB=6 cm,D为AB的中点,DE⊥AC于点E,∠A=30°,求BC,CD,AC的长.
15.(8分)如图,在菱形ABCD中,AE⊥BC于点E,若AB=5,AC=6,求AE的长.
16.(8分)如图,四边形ABCD是正方形,E是BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于点F.求证:AE=EF.
17.(10分)如图,在 ABCD中,AB=2AD,E为AB的中点,连接DE,EC.
(1)求证:DE⊥EC.
(2)若AD=5 cm,CE=8 cm,求△CDE的周长.
18.(12分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD.
(2)当点D为AB中点时,四边形BECD是什么特殊四边形 说明你的理由.
(3)若点D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形 请说明你的理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C C D B B A A
1.D 【解析】 ∵四边形ABCD是平行四边形,∴AB=CD=3 cm,BC=AD=5 cm,∴ ABCD的周长=2(AB+BC)=2×8=16(cm).
2.C 【解析】根据对角线相等的平行四边形是矩形可知C选项正确.
3.C 【解析】∵D,E分别是AB,AC的中点,∴DE是△ABC的中位线,∴BC=2DE=2×3=6.
4.D 【解析】由直线a∥b,CD⊥b,得线段CD的长度是直线a,b之间距离.
5.B 【解析】∵∠ACB=90°,点D为AB的中点,∴CD=AB=5.
6.B 【解析】∵四边形ABCD是菱形,∴∠A=∠BCD,AB=AD,∵∠1=55°,∠2=15°,∴∠BCD=180°-55°-15°=110°,∴∠A=110°,∴∠ABD=∠ADB=×(180°-110°)=35°.
7.A 【解析】 ∵矩形ABCD的面积S1=2S△ABD,S△ABD=BD·BF=S矩形BDEF,∴S1=S2.
8.A 【解析】 ∵四边形ABCD是正方形,∴∠DAF=∠B=90°,BC=AB=AD=2,∴∠BAE+∠2=90°,∵AB=2,E是BC的中点,∴BE=1,∴AE===,∵AD∥BC,∴∠1=∠2,∵DF⊥AE,∴∠1+∠ADF=90°,∴∠ADF=∠BAE,在△ADF和△BAE中,,∴△ADF≌△BAE(ASA),∴DF=AE=.
二、填空题
9 10 11 12
答案不唯一, 如AD=BC 或AB∥CD 150° 120 20
10.150° 【解析】由题意,得OA=OD,∴∠ADO=∠DAO=75°,∴ ∠COD=∠ADO+∠DAO=150°.
11.120 【解析】如图,设AC,BD的交点为E,∵四边形ABCD是菱形,∴AC⊥BD,BE=DE=5 cm,AE=CE,在Rt△ABE中,
AE===12 (cm),∴AC=24 cm,∴S菱形ABCD=AC·BD=×24×10=120(cm2).
12.20 【解析】如图1,2中,连接AC.在图2中,∵四边形ABCD是正方形,∴AB=BC,∠B=90°,∵AC=40 cm,∴AB=BC=20 cm,在图1中,∵∠B=60°,BA=BC,∴△ABC是等边三角形,∴AC=BC=20 cm.
三、解答题
13.证明:∵AE⊥BD,CF⊥BD,∴∠AED=∠BFC=90°,
∵BE=DF,∴BE+EF=DF+EF,即BF=DE, (3分)
又∵∠1=∠2,∴△ADE≌△CBF(ASA),∴AD=BC, (4分)
又∵∠1=∠2,∴AD∥BC,
∴四边形ABCD是平行四边形. (6分)
14.解:∵∠ACB=90°,AB=6 cm,D为AB的中点,∴CD=AB=3 cm; (3分)
∵∠A=30°,∴BC=AB=×6=3 cm; (6分)
由勾股定理,得AC===3(cm). (8分)
15.解:如图,连接BD,交AC于点O. (1分)
∵四边形ABCD是菱形,∴BC=AB=5,OA=OC=AC=3,OB=OD,AC⊥BD. (3分)
在Rt△AOB中,由勾股定理,得OB===4,∴BD=2OB=8. (5分)
∵S菱形ABCD=BC·AE=AC·BD=24,∴5AE=24,∴AE=. (8分)
16.证明:如图,取AB的中点H,连接EH.
∵∠AEF=90°,∴∠2+∠AEB=90°, (1分)
∵四边形ABCD是正方形,
∴∠1+∠AEB=90°,∴∠1=∠2, (2分)
∵E是BC的中点,H是AB的中点,且AB=BC,
∴BH=BE,AH=CE,∴∠BHE=45°, (4分)
∵CF是∠DCG的平分线,∴∠FCG=45°,
∴∠AHE=∠ECF=135°. (6分)
在△AHE和△ECF中,
,
∴△AHE≌△ECF(ASA),∴AE=EF. (8分)
17.解:(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∠ADC+∠BCD=180°,
∴∠AED=∠CDE, (2分)
∵E为AB的中点,∴AE=BE,
∵AB=2AD,∴AD=AE,∴∠ADE=∠AED,∴∠ADE=∠CDE,
同理可证:∠DCE=∠BCE,
∴∠EDC+∠ECD=×180°=90°,∴∠DEC=90°,即DE⊥EC. (6分)
(2)∵四边形ABCD是平行四边形,∴AB=DC=2AD=10 cm,
由(1)知∠DEC=90°,∴DE===6(cm),
∴△CDE的周长=DC+DE+CE=10+6+8=24(cm). (10分)
18.解:(1)证明:∵DE⊥BC,∴∠DFB=90°.
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE. (2分)
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD. (4分)
(2)四边形BECD是菱形. (5分)
理由:∵D为AB中点,∴AD=BD.
∵CE=AD,∴BD=CE,∵BD∥CE,∴四边形BECD是平行四边形.
又∵DE⊥BC,∴四边形BECD是菱形. (8分)
(3)当∠A=45°时,四边形BECD是正方形. (9分)
理由:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°,∴AC=BC.
∵D为AB中点,∴CD⊥AB,∴∠CDB=90°.
∵四边形BECD是菱形,∴四边形BECD是正方形.
即当∠A=45°时,四边形BECD是正方形. (12分)
基础过关测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.在 ABCD中,AB=3 cm,BC=5 cm,则 ABCD的周长是 ( )
A.8 cm B.14 cm C.15 cm D.16 cm
2.在 ABCD中,对角线AC,BD相交于点O,如果能够判定 ABCD为矩形,那么还需添加的条件是 ( )
A.AB=BC B.AB=AC C.OA=OB D.AC⊥BD
3.如图,在△ABC中,D,E分别是AB,AC的中点,如果DE=3,那么BC的长为 ( )
A.4 B.5 C.6 D.7
4.如图,直线a∥b,CD⊥直线b,则直线a,b之间的距离是 ( )
A.线段AB的长度 B.线段GH的长度
C.线段EF的长度 D.线段CD的长度
5.如图,在△ABC中,∠ACB=90°,AB=10,D是AB的中点,则CD= ( )
A.4 B.5 C.6 D.8
6.如图,菱形ABCD的顶点C在直线MN上,若∠1=55°,∠2=15°,则∠ABD的度数为 ( )
A.20° B.35° C.40° D.50°
7.如图,矩形ABCD和矩形BDEF,点A在EF边上,设矩形ABCD和矩形BDEF的面积分别为S1,S2,则S1与S2的大小关系为 ( )
A.S1=S2 B.S1>S2 C.S1
A. B. C.2 D.3
二、填空题(每小题4分,共16分)
9.在四边形ABCD中,∠A+∠B=180°,添加条件 (填一个即可),则可使四边形ABCD成为平行四边形.
10.如图,在矩形ABCD中,对角线AC,BD相交于点O,如果∠ADO=75°,那么∠COD的度数是 .
11.菱形ABCD的边长为13 cm,其中对角线BD长10 cm,则菱形ABCD的面积为 cm2.
12.小明用四根长度相同的木条制作了能够活动的菱形学具,他先把活动学具制作成为图1所示的菱形,并测得∠B=60°,接着把活动学具制作成为图2所示的正方形,并测得正方形的对角线AC=40 cm,则图1中对角线AC的长为 cm.
三、解答题(本大题共6小题,共52分)
13.(6分)如图,AE⊥BD于点E,CF⊥BD于点F,∠1=∠2,BE=DF,连接AB,CD.求证:四边形ABCD是平行四边形.
14.(8分)如图,在Rt△ABC中,∠ACB=90°,AB=6 cm,D为AB的中点,DE⊥AC于点E,∠A=30°,求BC,CD,AC的长.
15.(8分)如图,在菱形ABCD中,AE⊥BC于点E,若AB=5,AC=6,求AE的长.
16.(8分)如图,四边形ABCD是正方形,E是BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于点F.求证:AE=EF.
17.(10分)如图,在 ABCD中,AB=2AD,E为AB的中点,连接DE,EC.
(1)求证:DE⊥EC.
(2)若AD=5 cm,CE=8 cm,求△CDE的周长.
18.(12分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD.
(2)当点D为AB中点时,四边形BECD是什么特殊四边形 说明你的理由.
(3)若点D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形 请说明你的理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C C D B B A A
1.D 【解析】 ∵四边形ABCD是平行四边形,∴AB=CD=3 cm,BC=AD=5 cm,∴ ABCD的周长=2(AB+BC)=2×8=16(cm).
2.C 【解析】根据对角线相等的平行四边形是矩形可知C选项正确.
3.C 【解析】∵D,E分别是AB,AC的中点,∴DE是△ABC的中位线,∴BC=2DE=2×3=6.
4.D 【解析】由直线a∥b,CD⊥b,得线段CD的长度是直线a,b之间距离.
5.B 【解析】∵∠ACB=90°,点D为AB的中点,∴CD=AB=5.
6.B 【解析】∵四边形ABCD是菱形,∴∠A=∠BCD,AB=AD,∵∠1=55°,∠2=15°,∴∠BCD=180°-55°-15°=110°,∴∠A=110°,∴∠ABD=∠ADB=×(180°-110°)=35°.
7.A 【解析】 ∵矩形ABCD的面积S1=2S△ABD,S△ABD=BD·BF=S矩形BDEF,∴S1=S2.
8.A 【解析】 ∵四边形ABCD是正方形,∴∠DAF=∠B=90°,BC=AB=AD=2,∴∠BAE+∠2=90°,∵AB=2,E是BC的中点,∴BE=1,∴AE===,∵AD∥BC,∴∠1=∠2,∵DF⊥AE,∴∠1+∠ADF=90°,∴∠ADF=∠BAE,在△ADF和△BAE中,,∴△ADF≌△BAE(ASA),∴DF=AE=.
二、填空题
9 10 11 12
答案不唯一, 如AD=BC 或AB∥CD 150° 120 20
10.150° 【解析】由题意,得OA=OD,∴∠ADO=∠DAO=75°,∴ ∠COD=∠ADO+∠DAO=150°.
11.120 【解析】如图,设AC,BD的交点为E,∵四边形ABCD是菱形,∴AC⊥BD,BE=DE=5 cm,AE=CE,在Rt△ABE中,
AE===12 (cm),∴AC=24 cm,∴S菱形ABCD=AC·BD=×24×10=120(cm2).
12.20 【解析】如图1,2中,连接AC.在图2中,∵四边形ABCD是正方形,∴AB=BC,∠B=90°,∵AC=40 cm,∴AB=BC=20 cm,在图1中,∵∠B=60°,BA=BC,∴△ABC是等边三角形,∴AC=BC=20 cm.
三、解答题
13.证明:∵AE⊥BD,CF⊥BD,∴∠AED=∠BFC=90°,
∵BE=DF,∴BE+EF=DF+EF,即BF=DE, (3分)
又∵∠1=∠2,∴△ADE≌△CBF(ASA),∴AD=BC, (4分)
又∵∠1=∠2,∴AD∥BC,
∴四边形ABCD是平行四边形. (6分)
14.解:∵∠ACB=90°,AB=6 cm,D为AB的中点,∴CD=AB=3 cm; (3分)
∵∠A=30°,∴BC=AB=×6=3 cm; (6分)
由勾股定理,得AC===3(cm). (8分)
15.解:如图,连接BD,交AC于点O. (1分)
∵四边形ABCD是菱形,∴BC=AB=5,OA=OC=AC=3,OB=OD,AC⊥BD. (3分)
在Rt△AOB中,由勾股定理,得OB===4,∴BD=2OB=8. (5分)
∵S菱形ABCD=BC·AE=AC·BD=24,∴5AE=24,∴AE=. (8分)
16.证明:如图,取AB的中点H,连接EH.
∵∠AEF=90°,∴∠2+∠AEB=90°, (1分)
∵四边形ABCD是正方形,
∴∠1+∠AEB=90°,∴∠1=∠2, (2分)
∵E是BC的中点,H是AB的中点,且AB=BC,
∴BH=BE,AH=CE,∴∠BHE=45°, (4分)
∵CF是∠DCG的平分线,∴∠FCG=45°,
∴∠AHE=∠ECF=135°. (6分)
在△AHE和△ECF中,
,
∴△AHE≌△ECF(ASA),∴AE=EF. (8分)
17.解:(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∠ADC+∠BCD=180°,
∴∠AED=∠CDE, (2分)
∵E为AB的中点,∴AE=BE,
∵AB=2AD,∴AD=AE,∴∠ADE=∠AED,∴∠ADE=∠CDE,
同理可证:∠DCE=∠BCE,
∴∠EDC+∠ECD=×180°=90°,∴∠DEC=90°,即DE⊥EC. (6分)
(2)∵四边形ABCD是平行四边形,∴AB=DC=2AD=10 cm,
由(1)知∠DEC=90°,∴DE===6(cm),
∴△CDE的周长=DC+DE+CE=10+6+8=24(cm). (10分)
18.解:(1)证明:∵DE⊥BC,∴∠DFB=90°.
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE. (2分)
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD. (4分)
(2)四边形BECD是菱形. (5分)
理由:∵D为AB中点,∴AD=BD.
∵CE=AD,∴BD=CE,∵BD∥CE,∴四边形BECD是平行四边形.
又∵DE⊥BC,∴四边形BECD是菱形. (8分)
(3)当∠A=45°时,四边形BECD是正方形. (9分)
理由:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°,∴AC=BC.
∵D为AB中点,∴CD⊥AB,∴∠CDB=90°.
∵四边形BECD是菱形,∴四边形BECD是正方形.
即当∠A=45°时,四边形BECD是正方形. (12分)
