第十八章 平行四边形 能力提优测试卷(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十八章 平行四边形 能力提优测试卷(含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 169.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:20:53 | ||
图片预览


文档简介
第十八章 平行四边形
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.如图,平行四边形ABCD的对角线相交于点O,且两条对角线的和为34 cm,AB的长为4 cm,则△OAB的周长为 ( )
A.23 cm B.22 cm C.21 cm D.19 cm
2.在下列条件中,不能判定四边形ABCD是平行四边形的是 ( )
A.∠A=∠C,∠B=∠D B.AB∥CD,AD∥BC
C.AB∥CD,AD=BC D.AB=CD,AD=BC
3.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是 ( )
A.7 B. C. D.10
4.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E.若PE=5,则两平行线AD与BC间的距离为 ( )
A.10 B.8 C.5 D.4
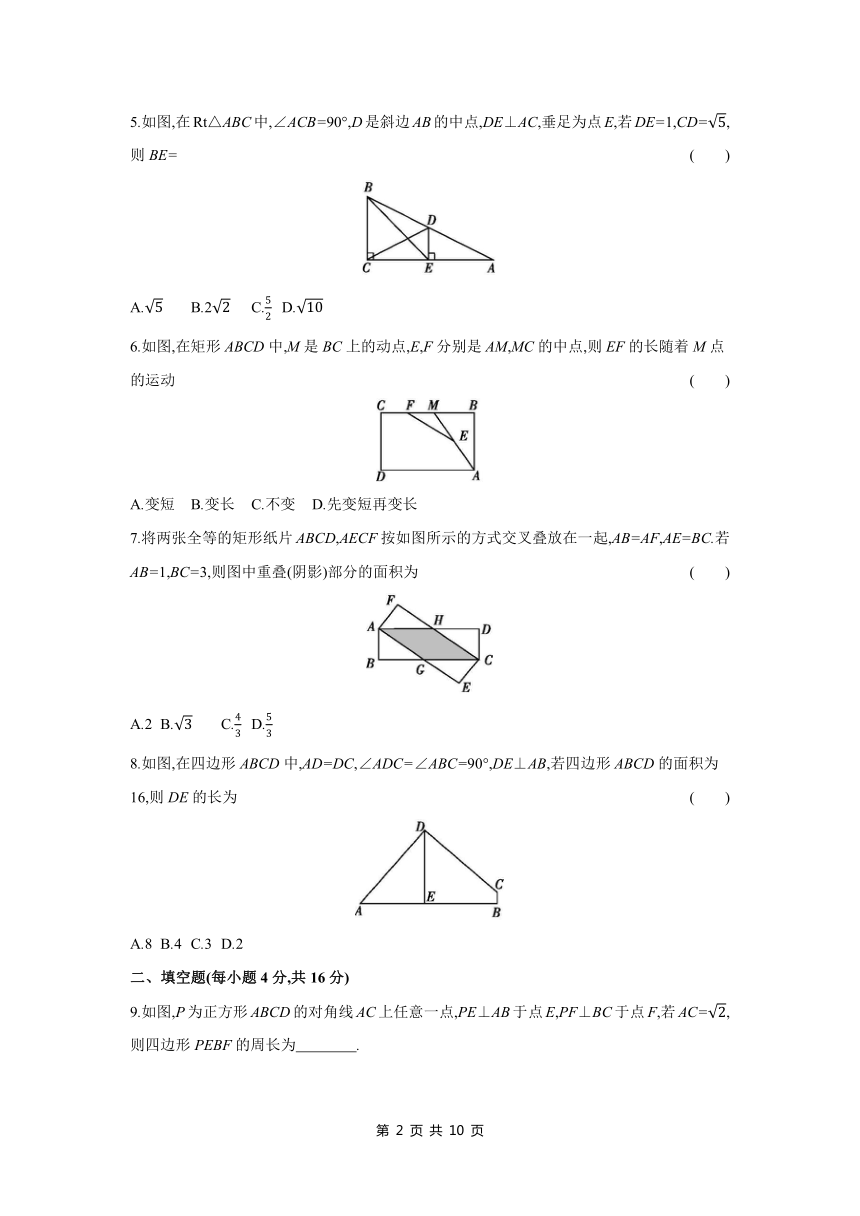
5.如图,在Rt△ABC中,∠ACB=90°,D是斜边AB的中点,DE⊥AC,垂足为点E,若DE=1,CD=,则BE= ( )
A. B.2 C. D.
6.如图,在矩形ABCD中,M是BC上的动点,E,F分别是AM,MC的中点,则EF的长随着M点的运动 ( )
A.变短 B.变长 C.不变 D.先变短再变长
7.将两张全等的矩形纸片ABCD,AECF按如图所示的方式交叉叠放在一起,AB=AF,AE=BC.若AB=1,BC=3,则图中重叠(阴影)部分的面积为 ( )
A.2 B. C. D.
8.如图,在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB,若四边形ABCD的面积为16,则DE的长为 ( )
A.8 B.4 C.3 D.2
二、填空题(每小题4分,共16分)
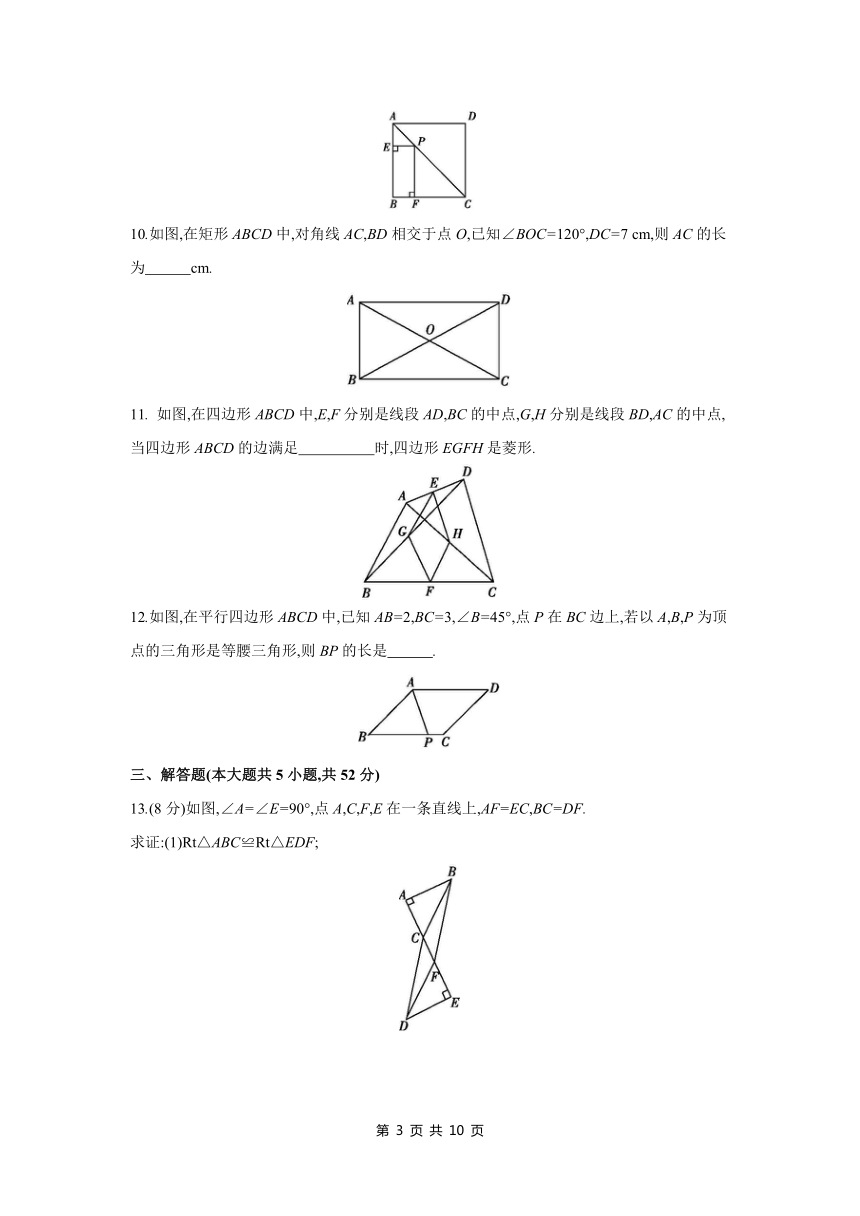
9.如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于点E,PF⊥BC于点F,若AC=,则四边形PEBF的周长为 .
10.如图,在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=7 cm,则AC的长为 cm.
11. 如图,在四边形ABCD中,E,F分别是线段AD,BC的中点,G,H分别是线段BD,AC的中点,当四边形ABCD的边满足 时,四边形EGFH是菱形.
12.如图,在平行四边形ABCD中,已知AB=2,BC=3,∠B=45°,点P在BC边上,若以A,B,P为顶点的三角形是等腰三角形,则BP的长是 .
三、解答题(本大题共5小题,共52分)
13.(8分)如图,∠A=∠E=90°,点A,C,F,E在一条直线上,AF=EC,BC=DF.
求证:(1)Rt△ABC≌Rt△EDF;
(2)四边形BCDF是平行四边形.
14.(8分)如图,在菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=4 cm.
(1)求BD的长;
(2)求菱形ABCD的面积.
15.(10分)如图,在△ABC中,∠C=2∠B,D是BC上一点,且AD⊥AB,E是BD的中点,连接AE.
(1)求证:BD=2AC.
(2)若AE=6.5,AD=5,求△ABE的周长.
16.(12分)如图,在 ABCD中,∠A=45°,过点D作ED⊥AD,交AB的延长线于点E,且BE=AB,连接BD,CE.
(1)求证:四边形BDCE是正方形.
(2)P为线段BC上一点,点M,N在直线AE上,且PM=PB,∠DPN=∠BPM.求证:AN=PB.
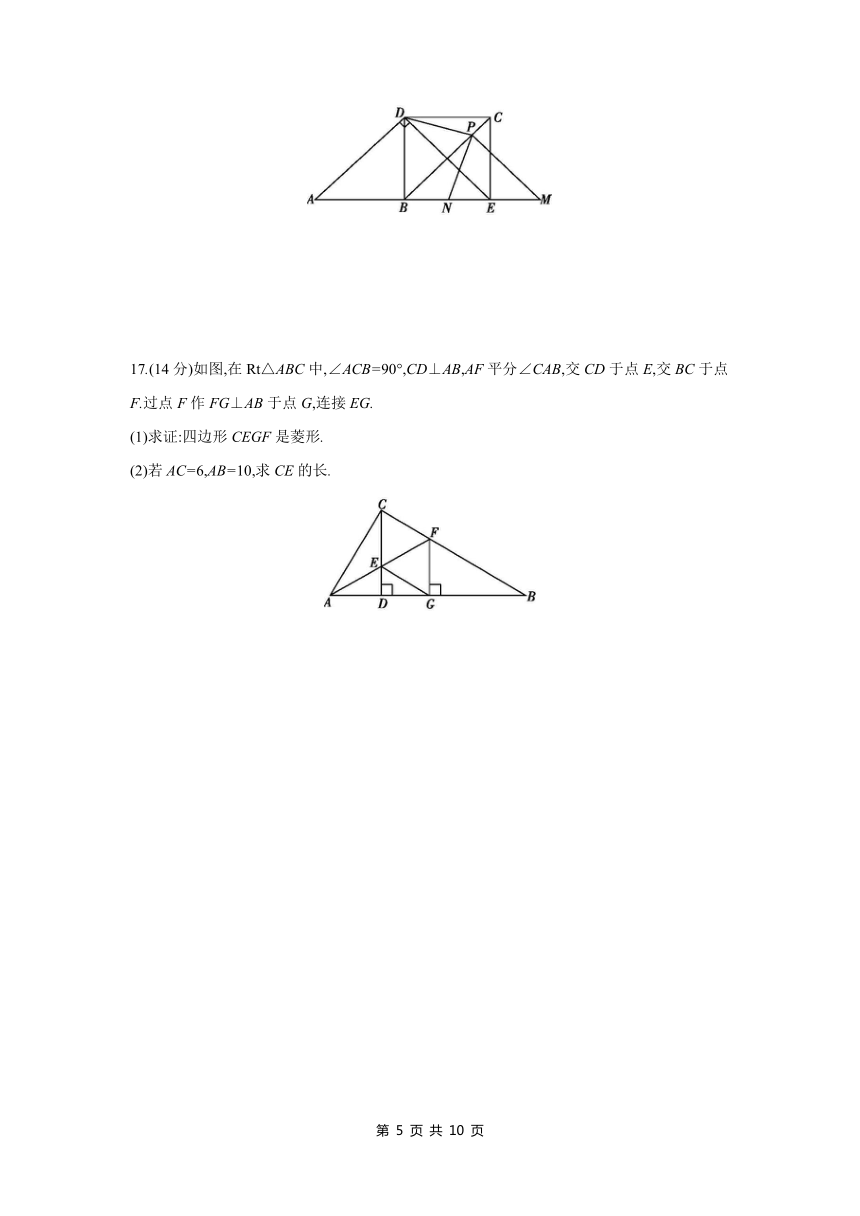
17.(14分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AF平分∠CAB,交CD于点E,交BC于点F.过点F作FG⊥AB于点G,连接EG.
(1)求证:四边形CEGF是菱形.
(2)若AC=6,AB=10,求CE的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C C B A B C D B
1.C 【解析】∵平行四边形的对角线互相平分,∴OA+OB=对角线和的一半,即OA+OB=17 cm.又∵AB的长为4 cm,∴△OAB的周长为17+4=21(cm).
2.C 【解析】根据两组对角分别相等的四边形是平行四边形,知A能;根据两组对边分别平行的四边形是平行四边形,知B能;根据两组对边分别相等的四边形是平行四边形,知D能.
3.B 【解析】在矩形OABC中,AC=OB,∵点B(2,5),∴OB==,∴A,C两点间的距离是.
4.A 【解析】如图,过点P作MN⊥AD,∵AD∥BC,∴MN⊥BC.∵∠ABC的平分线BP与∠BAD的平分线AP相交于点P,PE⊥AB,∴PM=PE=5,PE=PN=5,∴MN=5+5=10.
5.B 【解析】∵D是斜边AB的中点,∴CD=AD=BD,∵CD=,∴AB=2.∵∠ACB=90°,DE⊥AC,∴DE∥BC,CE=AE.又∵DE=1,∴BC=2.∴AC===4,∴CE=AC=2,∴BE=2.
6.C 【解析】如图,连接AC,∵E,F分别是AM,MC的中点,∴EF=AC.∵AC是定长,∴EF是定长.
7.D 【解析】∵四边形ABCD和四边形AECF是全等的矩形,∴AB=CE,∠B=∠E=90°,AD∥BC,AE∥CF,∴四边形AGCH是平行四边形.在△ABG和△CEG中,
,∴△ABG≌△CEG(AAS),∴AG=CG,∴四边形AGCH是菱形.设AG=CG=x,则BG=BC-CG=3-x,在Rt△ABG中,由勾股定理得12+(3-x)2=x2,解得x=,∴图中重叠(阴影)部分的面积=CG·AB=×1=.
8.B 【解析】过点D作BC的垂线,交BC的延长线于F,∵∠ADC=∠ABC=90°,∴∠A+∠BCD=180°,∵∠FCD+∠BCD=180°,∴∠A=∠FCD,又∠AED=∠F=90°,AD=DC,∴△ADE≌△CDF,∴DE=DF,∴四边形DEBF是正方形,S四边形ABCD=S正方形DEBF=16,∴DE=4.
二、填空题
9 10 11 12
2 14 AB=CD 2或2或
9.2 【解析】∵四边形ABCD是正方形,∴∠A=90°,AB=BC,∴AB2+BC2=AC2,∵AC=,∴AB=BC=1,∵四边形ABCD是正方形,∴∠BAC=∠BCA=45°,∵PE⊥AB,PF⊥BC,∴四边形PEBF为矩形,△AEP和△PFC为等腰直角三角形,∴PF=BE,PE=AE=BF,∴PE+PF+BE+BF=AE+BE+BE+AE=2AB=2,即四边形PEBF的周长为2.
10.14 【解析】在矩形ABCD中,OD=OC,∵∠BOC=120°,∴∠COD=60°,∴△COD是等边三角形,∴OC=DC=7 cm,∴AC=2OC=14 cm.
11.AB=CD 【解析】∵点E,G分别是AD,BD的中点,∴EG∥AB,EG=AB,同理:HF∥AB,HF=AB,∴EG∥HF,EG=HF,∴四边形EGFH是平行四边形.∵E,H分别是AD,AC的中点,∴EH=CD.当AB=CD时,有EG=EH,∴四边形EGFH是菱形.
12.2或2或 【解析】①当AB=BP=2时,△ABP是等腰三角形;②当AB=AP=2时,∵∠B=45°,∴△ABP是等腰直角三角形,BP=AB=2;③当BP=AP时,∵∠B=45°,∴△ABP是等腰直角三角形,易知BP=AB,∴BP==.综上所述,以A,B,P为顶点的三角形是等腰三角形,则BP的长是2或2或.
三、解答题
13.证明:(1)∵AF=EC,∴AC=EF.
又∵BC=DF,∠A=∠E=90°,
∴Rt△ABC≌Rt△EDF(HL). (3分)
(2)∵Rt△ABC≌Rt△EDF,
∴BC=DF,∠ACB=∠DFE,
∴180°-∠ACB=180°-∠DFE,
∴∠BCF=∠DFC,
∴BC∥DF,又∵BC=DF,
∴四边形BCDF是平行四边形. (8分)
14.解:(1)如图,连接AC,交BD于点O,
∵AE⊥BC于点E,且BE=CE,∴AB=AC.
∵在菱形ABCD中,∴AB=BC,
∴△ABC是等边三角形,∴∠ABO=30°.
∵AD=4,∴AB=4,AO=AC=2,
BO==2,∴BD=4. (5分)
(2)菱形ABCD的面积为AC BD=×4×4=8. (8分)
15.解:(1)证明:∵AD⊥AB,∴∠BAD=90°,
又∵点E是BD的中点,∴EA=BD=EB,
∴∠EAB=∠B,
∴∠AEC=2∠B,∵∠C=2∠B,
∴∠AEC=∠C,∴AE=AC,
∴BD=2AC. (5分)
(2)∵∠BAD=90°,点E是BD的中点,
∴BD=2AE=13,EA=EB=6.5.
由勾股定理,得AB===12.
∴△ABE的周长=AB+AE+BE=12+6.5+6.5=25. (10分)
16.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AB=BE,∴BE=CD,
∴四边形BDCE是平行四边形.
∵ED⊥AD,∠A=45°,∴∠A=∠DEA=45°,
∴AD=DE,
∴△ADE是等腰直角三角形,
又∵AB=BE,
∴DB=BE,DB⊥BE,
∴平行四边形BDCE是正方形. (5分)
(2)∵四边形BDCE是正方形,
∴BD=BE=AB,∠DBP=∠EBP=45°,
∵PM=PB,∴∠PBM=∠PMB=45°,∴∠BPM=90°.
∵∠DPN=∠BPM=90°,∴∠DPB=∠NPM.
在△DBP和△NMP中,
,
∴△DBP≌△NMP(ASA).
∴DB=NM,∴AB=NM,∴AN=BM.
∵BP=PM,∠BPM=90°,
∴BM=PB,∴AN=PB. (12分)
17.解:(1)证明:∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=FG,
在Rt△ACF与Rt△AGF中,
,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG. (2分)
∵CD⊥AB,FG⊥AB,∴CD∥FG,
∴∠CEF=∠EFG,
∴∠CEF=∠CFE,∴CE=CF,∴CE=FG,
∵CE∥FG,∴四边形CEGF是平行四边形.
∵CE=CF,∴平行四边形CEGF是菱形. (6分)
(2)∵四边形CEGF是菱形,
∴CE=GE.
∵∠ACB=90°,
∴BC===8. (8分)
由(1)得Rt△ACF≌Rt△AGF,∴AG=AC=6,BG=AB-AG=10-6=4. (11分)
设CE=CF=FG=x,则FB=8-x.
在Rt△BFG中,由勾股定理得x2+42=(8-x)2,解得x=3,
∴CE=3. (14分)
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.如图,平行四边形ABCD的对角线相交于点O,且两条对角线的和为34 cm,AB的长为4 cm,则△OAB的周长为 ( )
A.23 cm B.22 cm C.21 cm D.19 cm
2.在下列条件中,不能判定四边形ABCD是平行四边形的是 ( )
A.∠A=∠C,∠B=∠D B.AB∥CD,AD∥BC
C.AB∥CD,AD=BC D.AB=CD,AD=BC
3.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是 ( )
A.7 B. C. D.10
4.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E.若PE=5,则两平行线AD与BC间的距离为 ( )
A.10 B.8 C.5 D.4
5.如图,在Rt△ABC中,∠ACB=90°,D是斜边AB的中点,DE⊥AC,垂足为点E,若DE=1,CD=,则BE= ( )
A. B.2 C. D.
6.如图,在矩形ABCD中,M是BC上的动点,E,F分别是AM,MC的中点,则EF的长随着M点的运动 ( )
A.变短 B.变长 C.不变 D.先变短再变长
7.将两张全等的矩形纸片ABCD,AECF按如图所示的方式交叉叠放在一起,AB=AF,AE=BC.若AB=1,BC=3,则图中重叠(阴影)部分的面积为 ( )
A.2 B. C. D.
8.如图,在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB,若四边形ABCD的面积为16,则DE的长为 ( )
A.8 B.4 C.3 D.2
二、填空题(每小题4分,共16分)
9.如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于点E,PF⊥BC于点F,若AC=,则四边形PEBF的周长为 .
10.如图,在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=7 cm,则AC的长为 cm.
11. 如图,在四边形ABCD中,E,F分别是线段AD,BC的中点,G,H分别是线段BD,AC的中点,当四边形ABCD的边满足 时,四边形EGFH是菱形.
12.如图,在平行四边形ABCD中,已知AB=2,BC=3,∠B=45°,点P在BC边上,若以A,B,P为顶点的三角形是等腰三角形,则BP的长是 .
三、解答题(本大题共5小题,共52分)
13.(8分)如图,∠A=∠E=90°,点A,C,F,E在一条直线上,AF=EC,BC=DF.
求证:(1)Rt△ABC≌Rt△EDF;
(2)四边形BCDF是平行四边形.
14.(8分)如图,在菱形ABCD中,AE⊥BC于点E,且BE=CE,AD=4 cm.
(1)求BD的长;
(2)求菱形ABCD的面积.
15.(10分)如图,在△ABC中,∠C=2∠B,D是BC上一点,且AD⊥AB,E是BD的中点,连接AE.
(1)求证:BD=2AC.
(2)若AE=6.5,AD=5,求△ABE的周长.
16.(12分)如图,在 ABCD中,∠A=45°,过点D作ED⊥AD,交AB的延长线于点E,且BE=AB,连接BD,CE.
(1)求证:四边形BDCE是正方形.
(2)P为线段BC上一点,点M,N在直线AE上,且PM=PB,∠DPN=∠BPM.求证:AN=PB.
17.(14分)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AF平分∠CAB,交CD于点E,交BC于点F.过点F作FG⊥AB于点G,连接EG.
(1)求证:四边形CEGF是菱形.
(2)若AC=6,AB=10,求CE的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C C B A B C D B
1.C 【解析】∵平行四边形的对角线互相平分,∴OA+OB=对角线和的一半,即OA+OB=17 cm.又∵AB的长为4 cm,∴△OAB的周长为17+4=21(cm).
2.C 【解析】根据两组对角分别相等的四边形是平行四边形,知A能;根据两组对边分别平行的四边形是平行四边形,知B能;根据两组对边分别相等的四边形是平行四边形,知D能.
3.B 【解析】在矩形OABC中,AC=OB,∵点B(2,5),∴OB==,∴A,C两点间的距离是.
4.A 【解析】如图,过点P作MN⊥AD,∵AD∥BC,∴MN⊥BC.∵∠ABC的平分线BP与∠BAD的平分线AP相交于点P,PE⊥AB,∴PM=PE=5,PE=PN=5,∴MN=5+5=10.
5.B 【解析】∵D是斜边AB的中点,∴CD=AD=BD,∵CD=,∴AB=2.∵∠ACB=90°,DE⊥AC,∴DE∥BC,CE=AE.又∵DE=1,∴BC=2.∴AC===4,∴CE=AC=2,∴BE=2.
6.C 【解析】如图,连接AC,∵E,F分别是AM,MC的中点,∴EF=AC.∵AC是定长,∴EF是定长.
7.D 【解析】∵四边形ABCD和四边形AECF是全等的矩形,∴AB=CE,∠B=∠E=90°,AD∥BC,AE∥CF,∴四边形AGCH是平行四边形.在△ABG和△CEG中,
,∴△ABG≌△CEG(AAS),∴AG=CG,∴四边形AGCH是菱形.设AG=CG=x,则BG=BC-CG=3-x,在Rt△ABG中,由勾股定理得12+(3-x)2=x2,解得x=,∴图中重叠(阴影)部分的面积=CG·AB=×1=.
8.B 【解析】过点D作BC的垂线,交BC的延长线于F,∵∠ADC=∠ABC=90°,∴∠A+∠BCD=180°,∵∠FCD+∠BCD=180°,∴∠A=∠FCD,又∠AED=∠F=90°,AD=DC,∴△ADE≌△CDF,∴DE=DF,∴四边形DEBF是正方形,S四边形ABCD=S正方形DEBF=16,∴DE=4.
二、填空题
9 10 11 12
2 14 AB=CD 2或2或
9.2 【解析】∵四边形ABCD是正方形,∴∠A=90°,AB=BC,∴AB2+BC2=AC2,∵AC=,∴AB=BC=1,∵四边形ABCD是正方形,∴∠BAC=∠BCA=45°,∵PE⊥AB,PF⊥BC,∴四边形PEBF为矩形,△AEP和△PFC为等腰直角三角形,∴PF=BE,PE=AE=BF,∴PE+PF+BE+BF=AE+BE+BE+AE=2AB=2,即四边形PEBF的周长为2.
10.14 【解析】在矩形ABCD中,OD=OC,∵∠BOC=120°,∴∠COD=60°,∴△COD是等边三角形,∴OC=DC=7 cm,∴AC=2OC=14 cm.
11.AB=CD 【解析】∵点E,G分别是AD,BD的中点,∴EG∥AB,EG=AB,同理:HF∥AB,HF=AB,∴EG∥HF,EG=HF,∴四边形EGFH是平行四边形.∵E,H分别是AD,AC的中点,∴EH=CD.当AB=CD时,有EG=EH,∴四边形EGFH是菱形.
12.2或2或 【解析】①当AB=BP=2时,△ABP是等腰三角形;②当AB=AP=2时,∵∠B=45°,∴△ABP是等腰直角三角形,BP=AB=2;③当BP=AP时,∵∠B=45°,∴△ABP是等腰直角三角形,易知BP=AB,∴BP==.综上所述,以A,B,P为顶点的三角形是等腰三角形,则BP的长是2或2或.
三、解答题
13.证明:(1)∵AF=EC,∴AC=EF.
又∵BC=DF,∠A=∠E=90°,
∴Rt△ABC≌Rt△EDF(HL). (3分)
(2)∵Rt△ABC≌Rt△EDF,
∴BC=DF,∠ACB=∠DFE,
∴180°-∠ACB=180°-∠DFE,
∴∠BCF=∠DFC,
∴BC∥DF,又∵BC=DF,
∴四边形BCDF是平行四边形. (8分)
14.解:(1)如图,连接AC,交BD于点O,
∵AE⊥BC于点E,且BE=CE,∴AB=AC.
∵在菱形ABCD中,∴AB=BC,
∴△ABC是等边三角形,∴∠ABO=30°.
∵AD=4,∴AB=4,AO=AC=2,
BO==2,∴BD=4. (5分)
(2)菱形ABCD的面积为AC BD=×4×4=8. (8分)
15.解:(1)证明:∵AD⊥AB,∴∠BAD=90°,
又∵点E是BD的中点,∴EA=BD=EB,
∴∠EAB=∠B,
∴∠AEC=2∠B,∵∠C=2∠B,
∴∠AEC=∠C,∴AE=AC,
∴BD=2AC. (5分)
(2)∵∠BAD=90°,点E是BD的中点,
∴BD=2AE=13,EA=EB=6.5.
由勾股定理,得AB===12.
∴△ABE的周长=AB+AE+BE=12+6.5+6.5=25. (10分)
16.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AB=BE,∴BE=CD,
∴四边形BDCE是平行四边形.
∵ED⊥AD,∠A=45°,∴∠A=∠DEA=45°,
∴AD=DE,
∴△ADE是等腰直角三角形,
又∵AB=BE,
∴DB=BE,DB⊥BE,
∴平行四边形BDCE是正方形. (5分)
(2)∵四边形BDCE是正方形,
∴BD=BE=AB,∠DBP=∠EBP=45°,
∵PM=PB,∴∠PBM=∠PMB=45°,∴∠BPM=90°.
∵∠DPN=∠BPM=90°,∴∠DPB=∠NPM.
在△DBP和△NMP中,
,
∴△DBP≌△NMP(ASA).
∴DB=NM,∴AB=NM,∴AN=BM.
∵BP=PM,∠BPM=90°,
∴BM=PB,∴AN=PB. (12分)
17.解:(1)证明:∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=FG,
在Rt△ACF与Rt△AGF中,
,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG. (2分)
∵CD⊥AB,FG⊥AB,∴CD∥FG,
∴∠CEF=∠EFG,
∴∠CEF=∠CFE,∴CE=CF,∴CE=FG,
∵CE∥FG,∴四边形CEGF是平行四边形.
∵CE=CF,∴平行四边形CEGF是菱形. (6分)
(2)∵四边形CEGF是菱形,
∴CE=GE.
∵∠ACB=90°,
∴BC===8. (8分)
由(1)得Rt△ACF≌Rt△AGF,∴AG=AC=6,BG=AB-AG=10-6=4. (11分)
设CE=CF=FG=x,则FB=8-x.
在Rt△BFG中,由勾股定理得x2+42=(8-x)2,解得x=3,
∴CE=3. (14分)
