第十九章 一次函数 基础过关测试卷(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十九章 一次函数 基础过关测试卷(含答案) 2024-2025学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 106.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览

文档简介
第十九章 一次函数
基础过关测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.汽车以每小时90千米的速度匀速行驶,行驶的路程随时间的变化而变化.在这个变化过程中,自变量是 ( )
A.汽车 B.路程 C.速度 D.时间
2.下列函数中,y是x的正比例函数的是 ( )
A.y=3x+1 B.y=x-1 C.y=2x D.y=x2
3.“漏壶”是一种古代计时器.在壶内盛一定量的水,水从壶底的小孔漏出,壶内壁画有刻度,人们根据壶中水面的高度来计算时间.用x表示漏水时间,y表示壶底到水面的高度,不考虑水量变化对压力的影响,下列图象能表示y与x之间的函数关系的是 ( )
4.在函数y=中,自变量x的取值范围是 ( )
A.x>2 B.x≠2 C.x≤2 D.x<2
5.某超市购进了一些食品,出售时要在进价的基础上加一定的利润,其数量x(千克)与售价y(元)之间的关系如下表,则y关于x的函数解析式为( )
数量x/千克 1 2 3 4 5 …
售价y/元 6+0.5 12+1.0 18+1.5 24+2.0 30+2.5 …
A.y=6x+0.5 B.y=6+0.5x C.y=6.5x D.y=6.5+x
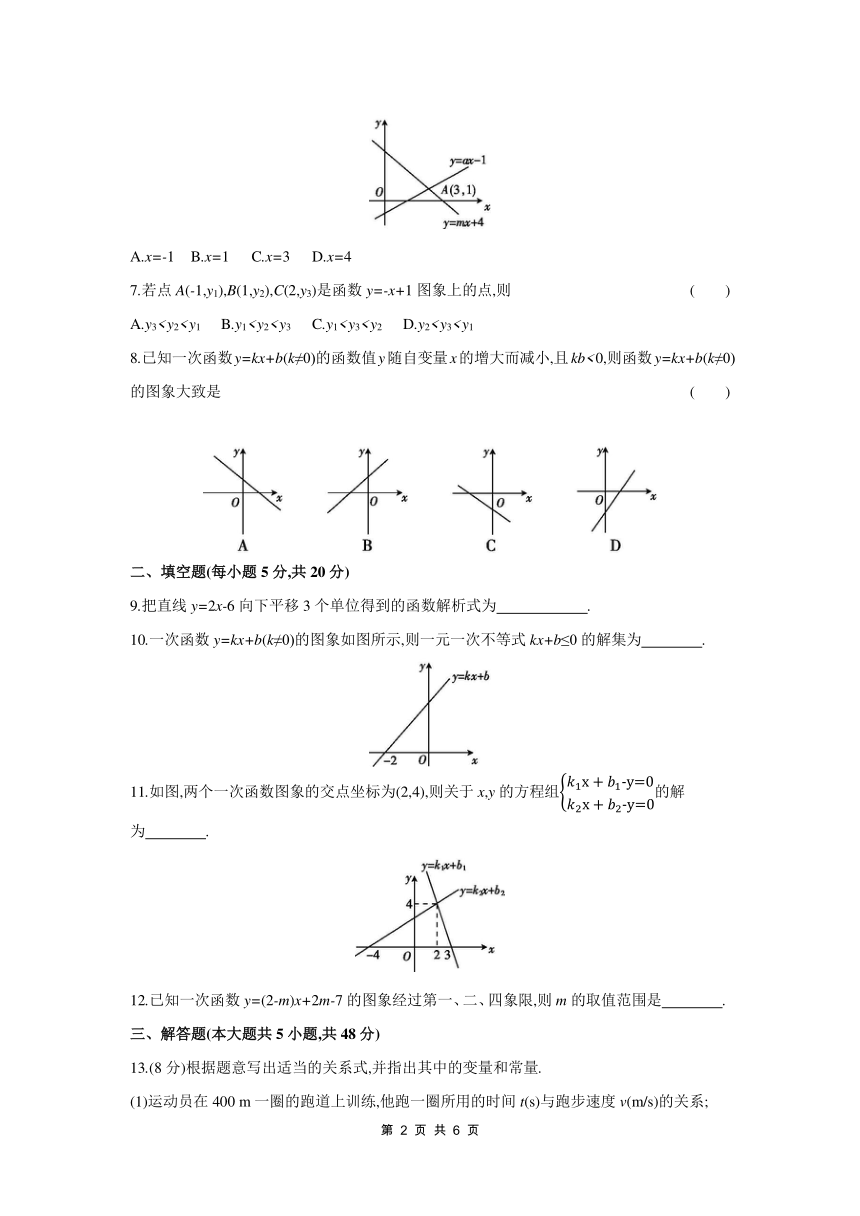
6.如图,已知一次函数y=ax-1与y=mx+4的图象相交于点A(3,1),则关于x的方程ax-1=mx+4的解是 ( )
A.x=-1 B.x=1 C.x=3 D.x=4
7.若点A(-1,y1),B(1,y2),C(2,y3)是函数y=-x+1图象上的点,则 ( )
A.y38.已知一次函数y=kx+b(k≠0)的函数值y随自变量x的增大而减小,且kb<0,则函数y=kx+b(k≠0)的图象大致是 ( )
二、填空题(每小题5分,共20分)
9.把直线y=2x-6向下平移3个单位得到的函数解析式为 .
10.一次函数y=kx+b(k≠0)的图象如图所示,则一元一次不等式kx+b≤0的解集为 .
11.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组的解为 .
12.已知一次函数y=(2-m)x+2m-7的图象经过第一、二、四象限,则m的取值范围是 .
三、解答题(本大题共5小题,共48分)
13.(8分)根据题意写出适当的关系式,并指出其中的变量和常量.
(1)运动员在400 m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步速度v(m/s)的关系;
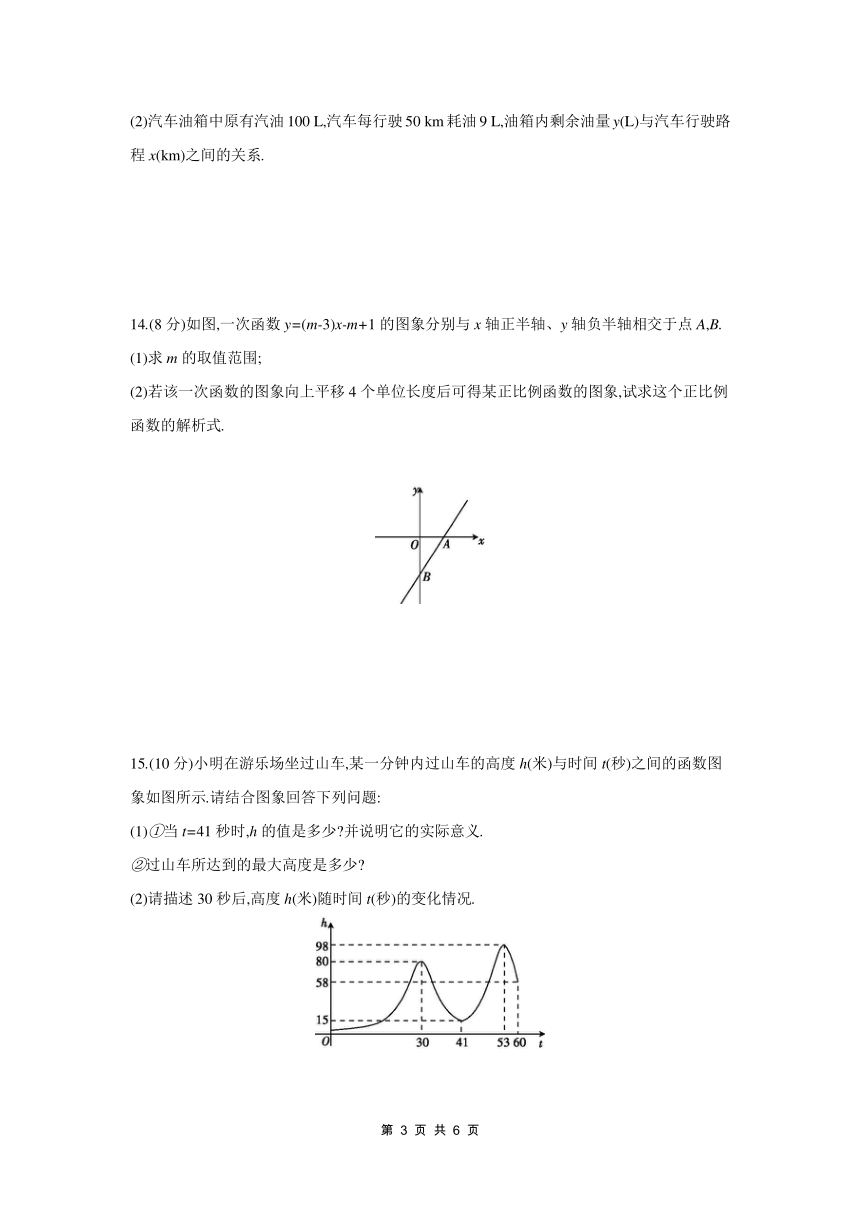
(2)汽车油箱中原有汽油100 L,汽车每行驶50 km耗油9 L,油箱内剩余油量y(L)与汽车行驶路程x(km)之间的关系.
14.(8分)如图,一次函数y=(m-3)x-m+1的图象分别与x轴正半轴、y轴负半轴相交于点A,B.
(1)求m的取值范围;
(2)若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象,试求这个正比例函数的解析式.
15.(10分)小明在游乐场坐过山车,某一分钟内过山车的高度h(米)与时间t(秒)之间的函数图象如图所示.请结合图象回答下列问题:
(1)①当t=41秒时,h的值是多少 并说明它的实际意义.
②过山车所达到的最大高度是多少
(2)请描述30秒后,高度h(米)随时间t(秒)的变化情况.
16.(10分)如图,在平面直角坐标系中,直线l1:y=x与直线l2:y=kx+b相交于点A,点A的横坐标为3,直线l2交y轴于点B,且OA=OB.
(1)试求直线l2的函数解析式;
(2)若P是y轴上一点,且△BPA的面积为6,请直接写出点P的坐标.
17.(12分)某单位计划元旦组织员工到某地旅游,A,B两旅行社的服务质量相同,且组织到该地旅游的价格都是每人300元.该单位在联系时,A旅行社表示可给予每位旅客七五折优惠,B旅行社表示可免去一位旅客的费用,其余八折优惠.
(1)当该单位旅游人数是多少时,支付给A,B两旅行社的总费用相同
(2)若该单位共有30人参加此次旅游,应选择哪家旅行社,使总费用更少
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C C B C C A A
1.D 【解析】匀速行驶,速度不变,速度是常量,时间是自变量.
3.C 【解析】∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,x表示漏水时间,y表示壶底到水面的高度,∴y随x的增大而减小.
4.B 【解析】由分母不为0,得x-2≠0,解得x≠2.
5.C 【解析】由表格中的数据可知售价与数量成倍数关系,即y=(6+0.5)x=6.5x.
6.C 【解析】由一次函数y=ax-1与y=mx+4的图象相交于点A(3,1),可知方程ax-1=mx+4的解是x=3.
7.A 【解析】∵k=-1<0,∴y随x的增大而减小,又∵-1<1<2,∴y38.A 【解析】根据“一次函数y=kx+b(k≠0),y随着x的增大而减小”,得k<0;根据“kb<0”,得b>0;则函数y=kx+b(k≠0)的图象经过第一、二、四象限.
二、填空题
9 10 11 12
y=2x-9 x≤-2 m>
10.x≤-2 【解析】由一次函数的图象可知当y≤0时,x的取值范围是x≤-2,所以一元一次不等式kx+b≤0的解集为x≤-2.
11. 【解析】两条直线的交点的横、纵坐标读数,即为联立这两条直线解析式的方程组之解.
12.m> 【解析】根据题意,得,解得m>.
三、解答题
13.解:(1)t=;其中v,t是变量,400是常量. (4分)
(2)y=100-x;其中x,y是变量,100,-是常量. (8分)
14.解:(1)由题意可知一次函数y=(m-3)x-m+1图象经过第一、三、四象限,
∴,解得m>3. (4分)
(2)将y=(m-3)x-m+1的图象向上平移4个单位长度后得y=(m-3)x-m+5,
由题意,得-m+5=0,解得m=5.
故这个正比例函数的解析式为y=2x. (8分)
15.解:(1)①当t=41秒时,h的值是15米.它的实际意义为当时间为41秒时,过山车的高度为15米. (2分)
②过山车所达到的最大高度是98米. (4分)
(2)当30当41当5316.解:(1)根据题意,点A的横坐标为3,代入直线y=x,得y=×3=4,即点A(3,4),
∴OA==5.
又∵OA=OB,∴OB=10,∴点B(0,-10). (3分)
将A,B两点坐标代入直线l2中,得,解得,
∴直线l2的解析式为y=x-10. (7分)
(2)点P 的坐标为(0,-6)或(0,-14). (10分)
17.解:(1)设A旅行社的费用为y1元,B旅行社的费用为y2元,该单位旅游人数为x人.
由题意,得y1=300×0.75x=225x, (2分)
y2=300×0.8×(x-1)=240x-240, (5分)
当y1=y2时,即225x=240x-240,解得x=16.
答:该单位的旅游人数为16人时,A,B两家旅行社所收费用相同. (7分)
(2)若选择A旅行社:y1=225×30=6750(元);
若选择B旅行社:y2=240×30-240=6960(元).
答:应选A旅行社总费用更少. (12分)
基础过关测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.汽车以每小时90千米的速度匀速行驶,行驶的路程随时间的变化而变化.在这个变化过程中,自变量是 ( )
A.汽车 B.路程 C.速度 D.时间
2.下列函数中,y是x的正比例函数的是 ( )
A.y=3x+1 B.y=x-1 C.y=2x D.y=x2
3.“漏壶”是一种古代计时器.在壶内盛一定量的水,水从壶底的小孔漏出,壶内壁画有刻度,人们根据壶中水面的高度来计算时间.用x表示漏水时间,y表示壶底到水面的高度,不考虑水量变化对压力的影响,下列图象能表示y与x之间的函数关系的是 ( )
4.在函数y=中,自变量x的取值范围是 ( )
A.x>2 B.x≠2 C.x≤2 D.x<2
5.某超市购进了一些食品,出售时要在进价的基础上加一定的利润,其数量x(千克)与售价y(元)之间的关系如下表,则y关于x的函数解析式为( )
数量x/千克 1 2 3 4 5 …
售价y/元 6+0.5 12+1.0 18+1.5 24+2.0 30+2.5 …
A.y=6x+0.5 B.y=6+0.5x C.y=6.5x D.y=6.5+x
6.如图,已知一次函数y=ax-1与y=mx+4的图象相交于点A(3,1),则关于x的方程ax-1=mx+4的解是 ( )
A.x=-1 B.x=1 C.x=3 D.x=4
7.若点A(-1,y1),B(1,y2),C(2,y3)是函数y=-x+1图象上的点,则 ( )
A.y3
二、填空题(每小题5分,共20分)
9.把直线y=2x-6向下平移3个单位得到的函数解析式为 .
10.一次函数y=kx+b(k≠0)的图象如图所示,则一元一次不等式kx+b≤0的解集为 .
11.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组的解为 .
12.已知一次函数y=(2-m)x+2m-7的图象经过第一、二、四象限,则m的取值范围是 .
三、解答题(本大题共5小题,共48分)
13.(8分)根据题意写出适当的关系式,并指出其中的变量和常量.
(1)运动员在400 m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步速度v(m/s)的关系;
(2)汽车油箱中原有汽油100 L,汽车每行驶50 km耗油9 L,油箱内剩余油量y(L)与汽车行驶路程x(km)之间的关系.
14.(8分)如图,一次函数y=(m-3)x-m+1的图象分别与x轴正半轴、y轴负半轴相交于点A,B.
(1)求m的取值范围;
(2)若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象,试求这个正比例函数的解析式.
15.(10分)小明在游乐场坐过山车,某一分钟内过山车的高度h(米)与时间t(秒)之间的函数图象如图所示.请结合图象回答下列问题:
(1)①当t=41秒时,h的值是多少 并说明它的实际意义.
②过山车所达到的最大高度是多少
(2)请描述30秒后,高度h(米)随时间t(秒)的变化情况.
16.(10分)如图,在平面直角坐标系中,直线l1:y=x与直线l2:y=kx+b相交于点A,点A的横坐标为3,直线l2交y轴于点B,且OA=OB.
(1)试求直线l2的函数解析式;
(2)若P是y轴上一点,且△BPA的面积为6,请直接写出点P的坐标.
17.(12分)某单位计划元旦组织员工到某地旅游,A,B两旅行社的服务质量相同,且组织到该地旅游的价格都是每人300元.该单位在联系时,A旅行社表示可给予每位旅客七五折优惠,B旅行社表示可免去一位旅客的费用,其余八折优惠.
(1)当该单位旅游人数是多少时,支付给A,B两旅行社的总费用相同
(2)若该单位共有30人参加此次旅游,应选择哪家旅行社,使总费用更少
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C C B C C A A
1.D 【解析】匀速行驶,速度不变,速度是常量,时间是自变量.
3.C 【解析】∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,x表示漏水时间,y表示壶底到水面的高度,∴y随x的增大而减小.
4.B 【解析】由分母不为0,得x-2≠0,解得x≠2.
5.C 【解析】由表格中的数据可知售价与数量成倍数关系,即y=(6+0.5)x=6.5x.
6.C 【解析】由一次函数y=ax-1与y=mx+4的图象相交于点A(3,1),可知方程ax-1=mx+4的解是x=3.
7.A 【解析】∵k=-1<0,∴y随x的增大而减小,又∵-1<1<2,∴y3
二、填空题
9 10 11 12
y=2x-9 x≤-2 m>
10.x≤-2 【解析】由一次函数的图象可知当y≤0时,x的取值范围是x≤-2,所以一元一次不等式kx+b≤0的解集为x≤-2.
11. 【解析】两条直线的交点的横、纵坐标读数,即为联立这两条直线解析式的方程组之解.
12.m> 【解析】根据题意,得,解得m>.
三、解答题
13.解:(1)t=;其中v,t是变量,400是常量. (4分)
(2)y=100-x;其中x,y是变量,100,-是常量. (8分)
14.解:(1)由题意可知一次函数y=(m-3)x-m+1图象经过第一、三、四象限,
∴,解得m>3. (4分)
(2)将y=(m-3)x-m+1的图象向上平移4个单位长度后得y=(m-3)x-m+5,
由题意,得-m+5=0,解得m=5.
故这个正比例函数的解析式为y=2x. (8分)
15.解:(1)①当t=41秒时,h的值是15米.它的实际意义为当时间为41秒时,过山车的高度为15米. (2分)
②过山车所达到的最大高度是98米. (4分)
(2)当30
∴OA==5.
又∵OA=OB,∴OB=10,∴点B(0,-10). (3分)
将A,B两点坐标代入直线l2中,得,解得,
∴直线l2的解析式为y=x-10. (7分)
(2)点P 的坐标为(0,-6)或(0,-14). (10分)
17.解:(1)设A旅行社的费用为y1元,B旅行社的费用为y2元,该单位旅游人数为x人.
由题意,得y1=300×0.75x=225x, (2分)
y2=300×0.8×(x-1)=240x-240, (5分)
当y1=y2时,即225x=240x-240,解得x=16.
答:该单位的旅游人数为16人时,A,B两家旅行社所收费用相同. (7分)
(2)若选择A旅行社:y1=225×30=6750(元);
若选择B旅行社:y2=240×30-240=6960(元).
答:应选A旅行社总费用更少. (12分)
