第十九章 一次函数 能力提优测试卷 (含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十九章 一次函数 能力提优测试卷 (含答案)2024-2025学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 188.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览


文档简介
第十九章 一次函数
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
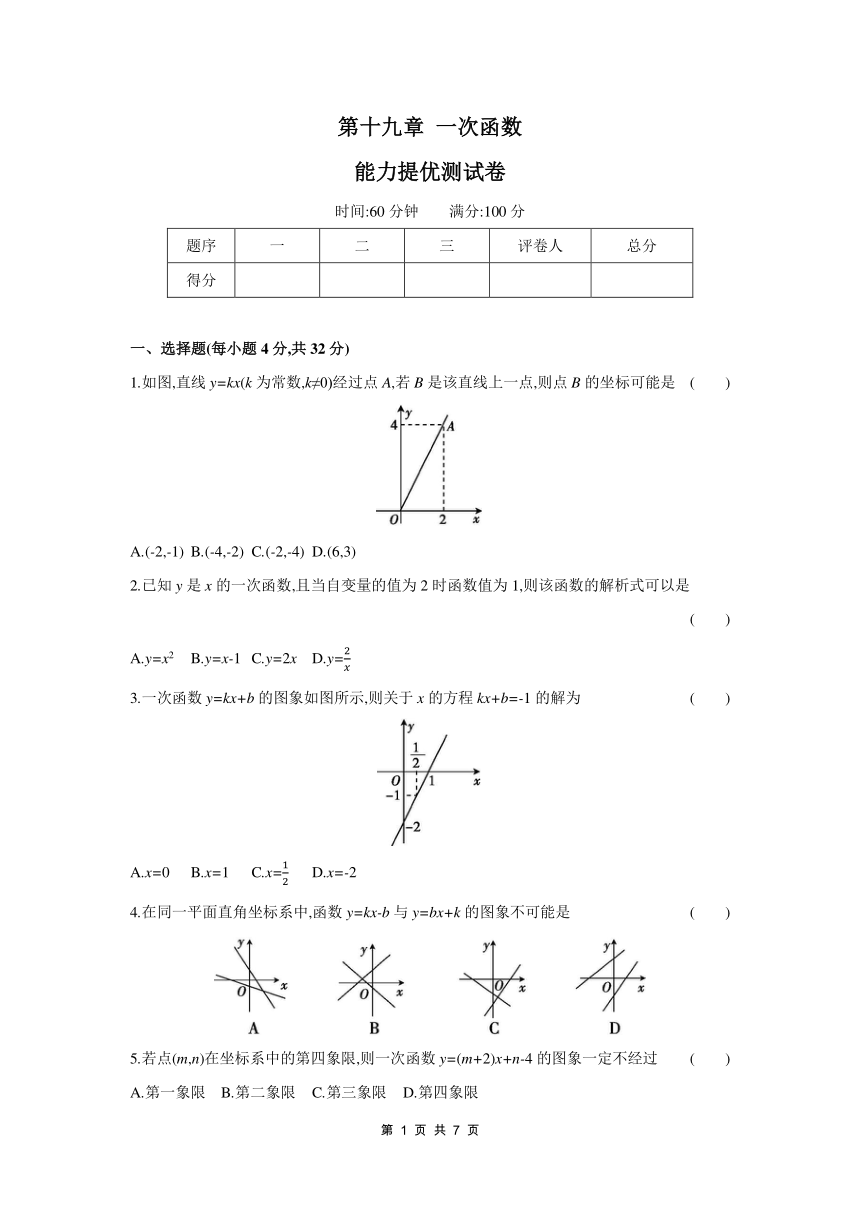
1.如图,直线y=kx(k为常数,k≠0)经过点A,若B是该直线上一点,则点B的坐标可能是 ( )
A.(-2,-1) B.(-4,-2) C.(-2,-4) D.(6,3)
2.已知y是x的一次函数,且当自变量的值为2时函数值为1,则该函数的解析式可以是 ( )
A.y=x2 B.y=x-1 C.y=2x D.y=
3.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=-1的解为 ( )
A.x=0 B.x=1 C.x= D.x=-2
4.在同一平面直角坐标系中,函数y=kx-b与y=bx+k的图象不可能是 ( )
5.若点(m,n)在坐标系中的第四象限,则一次函数y=(m+2)x+n-4的图象一定不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.A,B两地相距20 km,甲、乙两人沿同一条路线从A地到B地,如图,这是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:①甲的平均速度是4 km/h;②乙用了4个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
7.已知一次函数y=x+m和y=-x+n的图象都经过点A(-2,0),且分别交y轴于B,C两点,则△ABC的面积是 ( )
A.3 B.4 C.5 D.6
8.将正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置.点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点A2024的坐标是 ( )
A.(22023,22024) B.(22023-1,22023)
C.(22024,22023) D.(22022-1,22024)
二、填空题(每小题5分,共20分)
9.已知函数y=(1-3m)x+2024是一次函数,且y随x的增大而增大,则m的取值范围是 .
10.如图所示,直线y=x+1(记为l1)与直线y=mx+n(记为l2)相交于点P(a,2),则关于x的不等式x+1≤mx+n的解集为 .
11.已知点M(1,a)和点N(2,b)是一次函数y=-2x+n的图象上的两点,则a与b的大小关系是 .
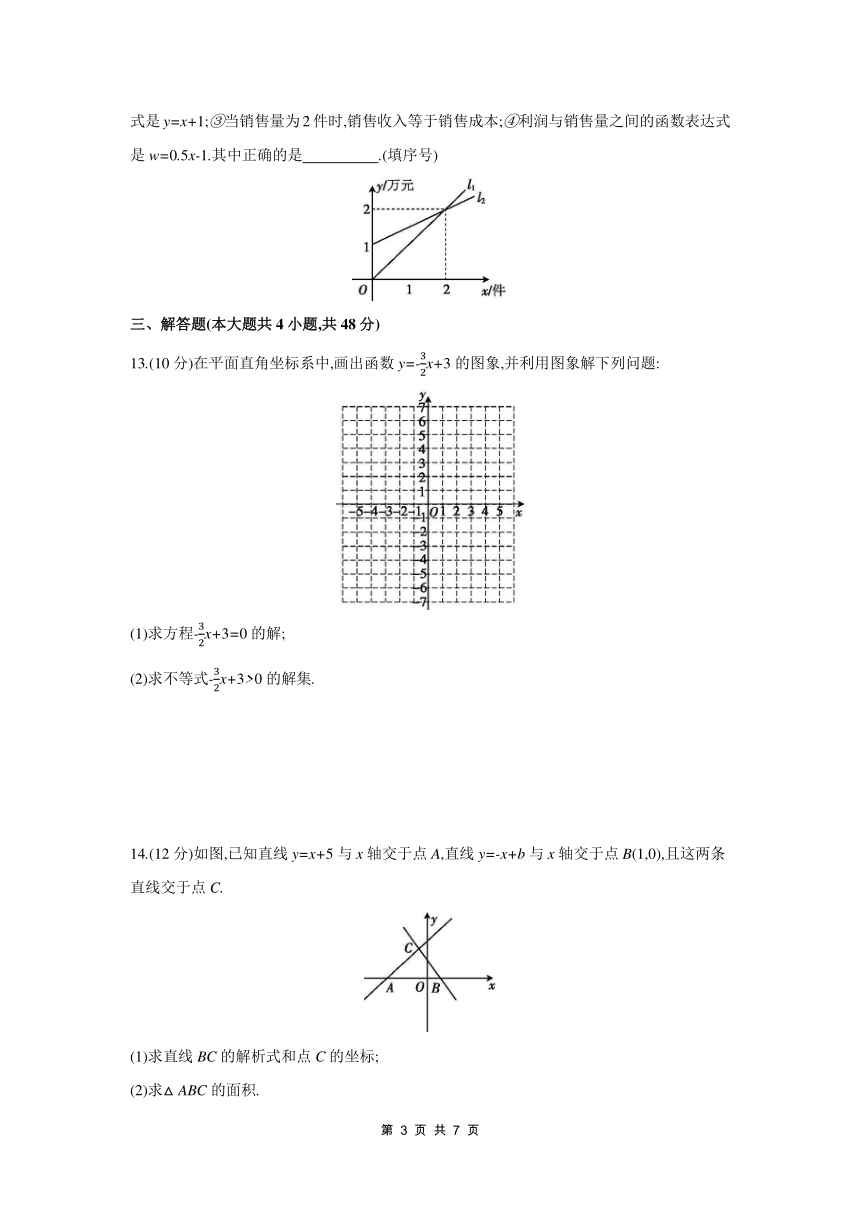
12.如图,l1表示某机床公司一天的销售收入与机床销售量的关系,l2表示该公司一天的销售成本与机床销售量的关系.有下列四个结论:①l1对应的函数解析式是y=x;② l2对应的函数解析式是y=x+1;③当销售量为2件时,销售收入等于销售成本;④利润与销售量之间的函数表达式是w=0.5x-1.其中正确的是 .(填序号)
三、解答题(本大题共4小题,共48分)
13.(10分)在平面直角坐标系中,画出函数y=-x+3的图象,并利用图象解下列问题:
(1)求方程-x+3=0的解;
(2)求不等式-x+3>0的解集.
14.(12分)如图,已知直线y=x+5与x轴交于点A,直线y=-x+b与x轴交于点B(1,0),且这两条直线交于点C.
(1)求直线BC的解析式和点C的坐标;
(2)求△ABC的面积.
15.(12分)为了保护学生的视力,课桌的高度y(cm)与椅子的高度x(cm)(不含靠背)都是按y是x的一次函数关系配套设计的,下表列出了两套课桌椅的高度:
第一套 第二套
椅子高度x/cm 40 30
课桌高度y/cm 80 70
(1)请确定y与x的函数解析式.(不要求写出x的取值范围)
(2)有一把高50 cm的椅子和一张高90 cm的课桌,它们是否配套 请通过计算说明理由.
16.(14分)如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数解析式;
(2)C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标.(用含a的代数式表示)
参考答案
一、选择题
1 2 3 4 5 6 7 8
C B C C B A D B
1.C 【解析】将A(2,4)代入直线y=kx,得2k=4,解得k=2,因此,直线的解析式为y=2x,当x=-2时,代入,得y=2×(-2)=-4,即点(-2,-4)在直线上.
2.B 【解析】当x=2时,y=x2=22=4,y=x-1=1,y=2x=2×2=4,y===1,又y是x的一次函数,故B正确.
3.C 【解析】∵一次函数y=kx+b的图象过点(,-1),∴关于x的方程kx+b=-1的解是x=.
4.C 【解析】A.当k<0,b<0时,函数图象满足;B.当k<0,b>0时,函数图象满足;C.没有合适的k,b满足图象;D.当k>0,b>0时,函数图象满足.
5.B 【解析】∵点(m,n)在坐标系中的第四象限,∴m>0,n<0,∴m+2>0,n-4<0,∴一次函数y=(m+2)x+n-4的图象经过第一、三、四象限.
6.A 【解析】①正确,②③④错误.
7.D 【解析】∵y=x+m和y=-x+n的图象都经过点A(-2,0),∴0=×(-2)+m,0=-×(-2)+n,解得m=5,n=-1,∴两个函数解析式分别为y=x+5,y=-x-1,∴B(0,5),C(0,-1),则BC=5-(-1)=6,∴S△ABC=BC·AO=×6×2=6.
8.B 【解析】当x=0时,y=x+1=0+1=1,∴点A1的坐标为(0,1).∵四边形A1B1C1O为正方形,∴点B1的坐标为(1,1),点C1的坐标为(1,0);当x=1时,y=x+1=1+1=2,∴点A2的坐标为(1,2).∵A2B2C2C1为正方形,∴点B2的坐标为(3,2),点C2的坐标为(3,0).同理,可知:点A3的坐标为(3,4),点A4的坐标为(7,8),点A5的坐标为(15,16),…∴点An的坐标为(2n-1-1,2n-1)(n为正整数),∴点A2024的坐标为(22023-1,22023).
二、填空题
9 10 11 12
m< x≤1 a>b ①③④
9.m< 【解析】根据题意,得1-3m>0,解得m<.
10.x≤1 【解析】当y=2时,a+1=2,解得a=1,∴由图可知x≤1时,x+1≤mx+n,∴关于x的不等式x+1≤mx+n的解集为x≤1.
11.a>b 【解析】∵一次函数y=-2x+n中,-2<0,∴y随x的增大而减小,∵点M(1,a)和点N(2,b)在y=-2x+n的图象上,1<2,∴a>b.
12.①③④ 【解析】观察图象可知直线l1经过原点,设l1的解析式为y1=kx,将点(2,2)代入解析式可得2=2k,解得k=1,所以l1 的解析式为y1=x,故①正确;观察图象可知直线l2不经过原点,设l2的解析式为y2=kx+b,将点(0,1),(2,2)代入解析式可得,解得,所以 l2的解析式为y2=x+1,故②错误;观察图象可知,直线 l2与直线 l1交于点(2,2),所以,当销售量为2时,销售收入等于销售成本,故③正确;利润=y1-y2=x-(x+1)=x-1,故④正确.
三、解答题
13.解:画出函数图象,如图. (4分)
(1)如图,∵直线与x轴的交点坐标为(2,0),
∴方程-x+3=0的解为x=2. (7分)
(2)如图,∵x<2时,y>0,
∴不等式-x+3>0的解集为x<2. (10分)
14.解:(1)把点B(1,0)代入直线y=-x+b得0=-1+b.解得b=1,
∴直线BC的解析式为y=-x+1, (2分)
联立两函数为,解得.
∴C(-2,3). (6分)
(2)把y=0代入y=x+5,
得x+5=0,解得x=-5.
∴点A的坐标为(-5,0). (9分)
∴△ABC的面积=AB·yC=×6×3=9. (12分)
15.解:(1)设y与x的函数关系式为y=kx+b,
将x=40,y=80和x=30,y=70代入,得,解得.
故y与x的函数关系式为y=x+40. (6分)
(2)它们是配套的. (7分)
理由:将x=50代入y=x+40,得y=50+40=90,故是配套的. (12分)
16.解:(1)设直线l1对应的函数解析式为y=k1x,把点(18,6)代入得18k1=6,解得k1=,
∴直线l1对应的函数解析式为y=x; (3分)
设直线l2对应的函数解析式为y=k2x+b,
把点A(0,24),B(18,6)代入得,解得,
∴直线l2对应的函数解析式为y=-x+24. (7分)
(2)∵点C在直线l1上,且点C的纵坐标为a,
∴a=x,∴x=3a,∴点C的坐标为(3a,a). (10分)
∵CD∥y轴,∴点D的横坐标为3a,
∵点D在直线l2上,∴y=-3a+24,
∴点D的坐标为(3a,-3a+24). (14分)
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.如图,直线y=kx(k为常数,k≠0)经过点A,若B是该直线上一点,则点B的坐标可能是 ( )
A.(-2,-1) B.(-4,-2) C.(-2,-4) D.(6,3)
2.已知y是x的一次函数,且当自变量的值为2时函数值为1,则该函数的解析式可以是 ( )
A.y=x2 B.y=x-1 C.y=2x D.y=
3.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=-1的解为 ( )
A.x=0 B.x=1 C.x= D.x=-2
4.在同一平面直角坐标系中,函数y=kx-b与y=bx+k的图象不可能是 ( )
5.若点(m,n)在坐标系中的第四象限,则一次函数y=(m+2)x+n-4的图象一定不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.A,B两地相距20 km,甲、乙两人沿同一条路线从A地到B地,如图,这是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:①甲的平均速度是4 km/h;②乙用了4个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
7.已知一次函数y=x+m和y=-x+n的图象都经过点A(-2,0),且分别交y轴于B,C两点,则△ABC的面积是 ( )
A.3 B.4 C.5 D.6
8.将正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示的方式放置.点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点A2024的坐标是 ( )
A.(22023,22024) B.(22023-1,22023)
C.(22024,22023) D.(22022-1,22024)
二、填空题(每小题5分,共20分)
9.已知函数y=(1-3m)x+2024是一次函数,且y随x的增大而增大,则m的取值范围是 .
10.如图所示,直线y=x+1(记为l1)与直线y=mx+n(记为l2)相交于点P(a,2),则关于x的不等式x+1≤mx+n的解集为 .
11.已知点M(1,a)和点N(2,b)是一次函数y=-2x+n的图象上的两点,则a与b的大小关系是 .
12.如图,l1表示某机床公司一天的销售收入与机床销售量的关系,l2表示该公司一天的销售成本与机床销售量的关系.有下列四个结论:①l1对应的函数解析式是y=x;② l2对应的函数解析式是y=x+1;③当销售量为2件时,销售收入等于销售成本;④利润与销售量之间的函数表达式是w=0.5x-1.其中正确的是 .(填序号)
三、解答题(本大题共4小题,共48分)
13.(10分)在平面直角坐标系中,画出函数y=-x+3的图象,并利用图象解下列问题:
(1)求方程-x+3=0的解;
(2)求不等式-x+3>0的解集.
14.(12分)如图,已知直线y=x+5与x轴交于点A,直线y=-x+b与x轴交于点B(1,0),且这两条直线交于点C.
(1)求直线BC的解析式和点C的坐标;
(2)求△ABC的面积.
15.(12分)为了保护学生的视力,课桌的高度y(cm)与椅子的高度x(cm)(不含靠背)都是按y是x的一次函数关系配套设计的,下表列出了两套课桌椅的高度:
第一套 第二套
椅子高度x/cm 40 30
课桌高度y/cm 80 70
(1)请确定y与x的函数解析式.(不要求写出x的取值范围)
(2)有一把高50 cm的椅子和一张高90 cm的课桌,它们是否配套 请通过计算说明理由.
16.(14分)如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数解析式;
(2)C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标.(用含a的代数式表示)
参考答案
一、选择题
1 2 3 4 5 6 7 8
C B C C B A D B
1.C 【解析】将A(2,4)代入直线y=kx,得2k=4,解得k=2,因此,直线的解析式为y=2x,当x=-2时,代入,得y=2×(-2)=-4,即点(-2,-4)在直线上.
2.B 【解析】当x=2时,y=x2=22=4,y=x-1=1,y=2x=2×2=4,y===1,又y是x的一次函数,故B正确.
3.C 【解析】∵一次函数y=kx+b的图象过点(,-1),∴关于x的方程kx+b=-1的解是x=.
4.C 【解析】A.当k<0,b<0时,函数图象满足;B.当k<0,b>0时,函数图象满足;C.没有合适的k,b满足图象;D.当k>0,b>0时,函数图象满足.
5.B 【解析】∵点(m,n)在坐标系中的第四象限,∴m>0,n<0,∴m+2>0,n-4<0,∴一次函数y=(m+2)x+n-4的图象经过第一、三、四象限.
6.A 【解析】①正确,②③④错误.
7.D 【解析】∵y=x+m和y=-x+n的图象都经过点A(-2,0),∴0=×(-2)+m,0=-×(-2)+n,解得m=5,n=-1,∴两个函数解析式分别为y=x+5,y=-x-1,∴B(0,5),C(0,-1),则BC=5-(-1)=6,∴S△ABC=BC·AO=×6×2=6.
8.B 【解析】当x=0时,y=x+1=0+1=1,∴点A1的坐标为(0,1).∵四边形A1B1C1O为正方形,∴点B1的坐标为(1,1),点C1的坐标为(1,0);当x=1时,y=x+1=1+1=2,∴点A2的坐标为(1,2).∵A2B2C2C1为正方形,∴点B2的坐标为(3,2),点C2的坐标为(3,0).同理,可知:点A3的坐标为(3,4),点A4的坐标为(7,8),点A5的坐标为(15,16),…∴点An的坐标为(2n-1-1,2n-1)(n为正整数),∴点A2024的坐标为(22023-1,22023).
二、填空题
9 10 11 12
m< x≤1 a>b ①③④
9.m< 【解析】根据题意,得1-3m>0,解得m<.
10.x≤1 【解析】当y=2时,a+1=2,解得a=1,∴由图可知x≤1时,x+1≤mx+n,∴关于x的不等式x+1≤mx+n的解集为x≤1.
11.a>b 【解析】∵一次函数y=-2x+n中,-2<0,∴y随x的增大而减小,∵点M(1,a)和点N(2,b)在y=-2x+n的图象上,1<2,∴a>b.
12.①③④ 【解析】观察图象可知直线l1经过原点,设l1的解析式为y1=kx,将点(2,2)代入解析式可得2=2k,解得k=1,所以l1 的解析式为y1=x,故①正确;观察图象可知直线l2不经过原点,设l2的解析式为y2=kx+b,将点(0,1),(2,2)代入解析式可得,解得,所以 l2的解析式为y2=x+1,故②错误;观察图象可知,直线 l2与直线 l1交于点(2,2),所以,当销售量为2时,销售收入等于销售成本,故③正确;利润=y1-y2=x-(x+1)=x-1,故④正确.
三、解答题
13.解:画出函数图象,如图. (4分)
(1)如图,∵直线与x轴的交点坐标为(2,0),
∴方程-x+3=0的解为x=2. (7分)
(2)如图,∵x<2时,y>0,
∴不等式-x+3>0的解集为x<2. (10分)
14.解:(1)把点B(1,0)代入直线y=-x+b得0=-1+b.解得b=1,
∴直线BC的解析式为y=-x+1, (2分)
联立两函数为,解得.
∴C(-2,3). (6分)
(2)把y=0代入y=x+5,
得x+5=0,解得x=-5.
∴点A的坐标为(-5,0). (9分)
∴△ABC的面积=AB·yC=×6×3=9. (12分)
15.解:(1)设y与x的函数关系式为y=kx+b,
将x=40,y=80和x=30,y=70代入,得,解得.
故y与x的函数关系式为y=x+40. (6分)
(2)它们是配套的. (7分)
理由:将x=50代入y=x+40,得y=50+40=90,故是配套的. (12分)
16.解:(1)设直线l1对应的函数解析式为y=k1x,把点(18,6)代入得18k1=6,解得k1=,
∴直线l1对应的函数解析式为y=x; (3分)
设直线l2对应的函数解析式为y=k2x+b,
把点A(0,24),B(18,6)代入得,解得,
∴直线l2对应的函数解析式为y=-x+24. (7分)
(2)∵点C在直线l1上,且点C的纵坐标为a,
∴a=x,∴x=3a,∴点C的坐标为(3a,a). (10分)
∵CD∥y轴,∴点D的横坐标为3a,
∵点D在直线l2上,∴y=-3a+24,
∴点D的坐标为(3a,-3a+24). (14分)
