第十七章 勾股定理 基础过关测试卷(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十七章 勾股定理 基础过关测试卷(含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 180.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:22:06 | ||
图片预览

文档简介
第十七章 勾股定理
基础过关测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.如图,在△ABC中,∠C=90°,若BC=3,AC=5,则AB= ( )
A.4 B.6 C.8 D.
2.小明想做一个直角三角形的木架,以下四组木棒中,能够刚好做成直角三角形木架的是 ( )
A.3 cm,4 cm,7 cm B.6 cm,8 cm,12 cm
C.7 cm,12 cm,15 cm D.8 cm,15 cm,17 cm
3.下列各命题的逆命题是真命题的是 ( )
A.全等三角形的对应角相等
B.有两边相等的三角形是等腰三角形
C.如果两个数相等,那么这两个数的绝对值相等
D.若a<0,b<0,则ab>0
4.下面各图中,不能证明勾股定理正确性的是 ( )
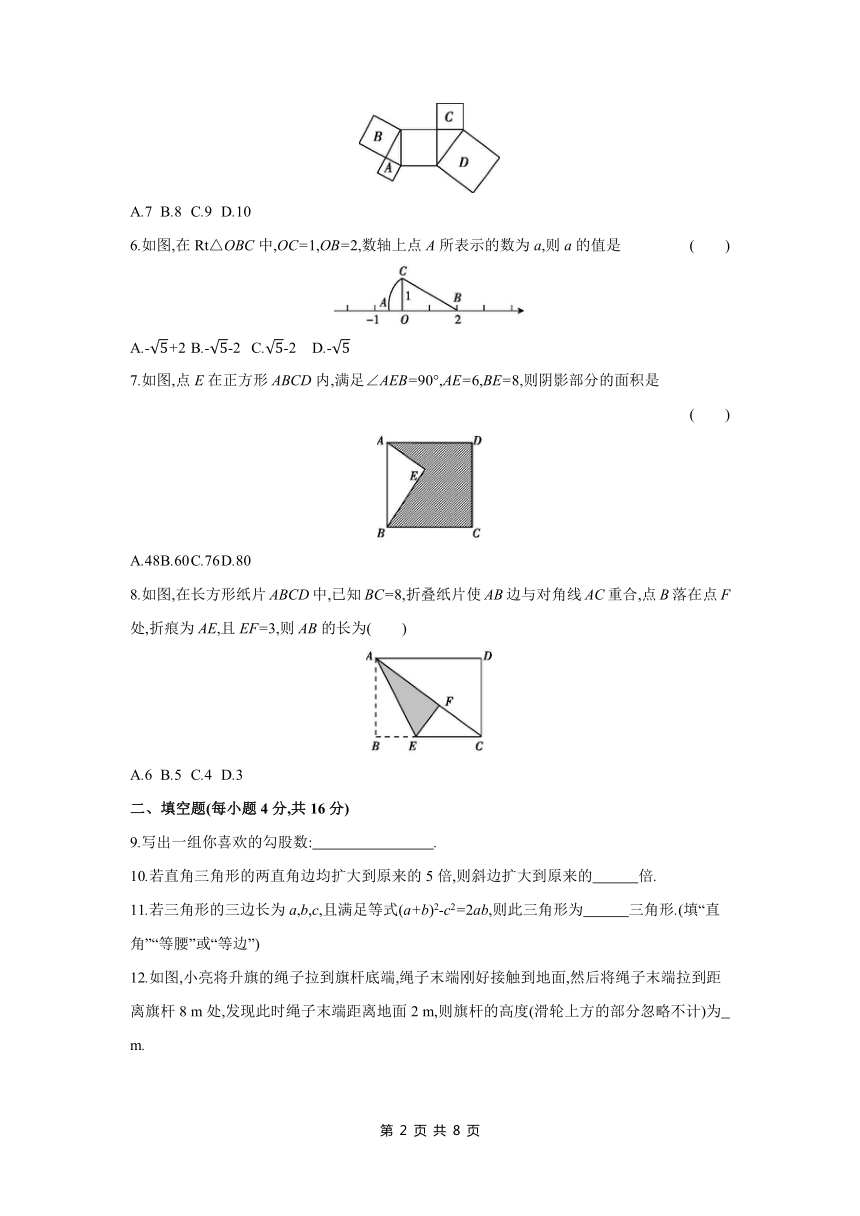
5.如图,图中所有四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次为2,4,3,则正方形D的面积为 ( )
A.7 B.8 C.9 D.10
6.如图,在Rt△OBC中,OC=1,OB=2,数轴上点A所表示的数为a,则a的值是 ( )
A.-+2 B.--2 C.-2 D.-
7.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是
( )
A.48 B.60 C.76 D.80
8.如图,在长方形纸片ABCD中,已知BC=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.6 B.5 C.4 D.3
二、填空题(每小题4分,共16分)
9.写出一组你喜欢的勾股数: .
10.若直角三角形的两直角边均扩大到原来的5倍,则斜边扩大到原来的 倍.
11.若三角形的三边长为a,b,c,且满足等式(a+b)2-c2=2ab,则此三角形为 三角形.(填“直角”“等腰”或“等边”)
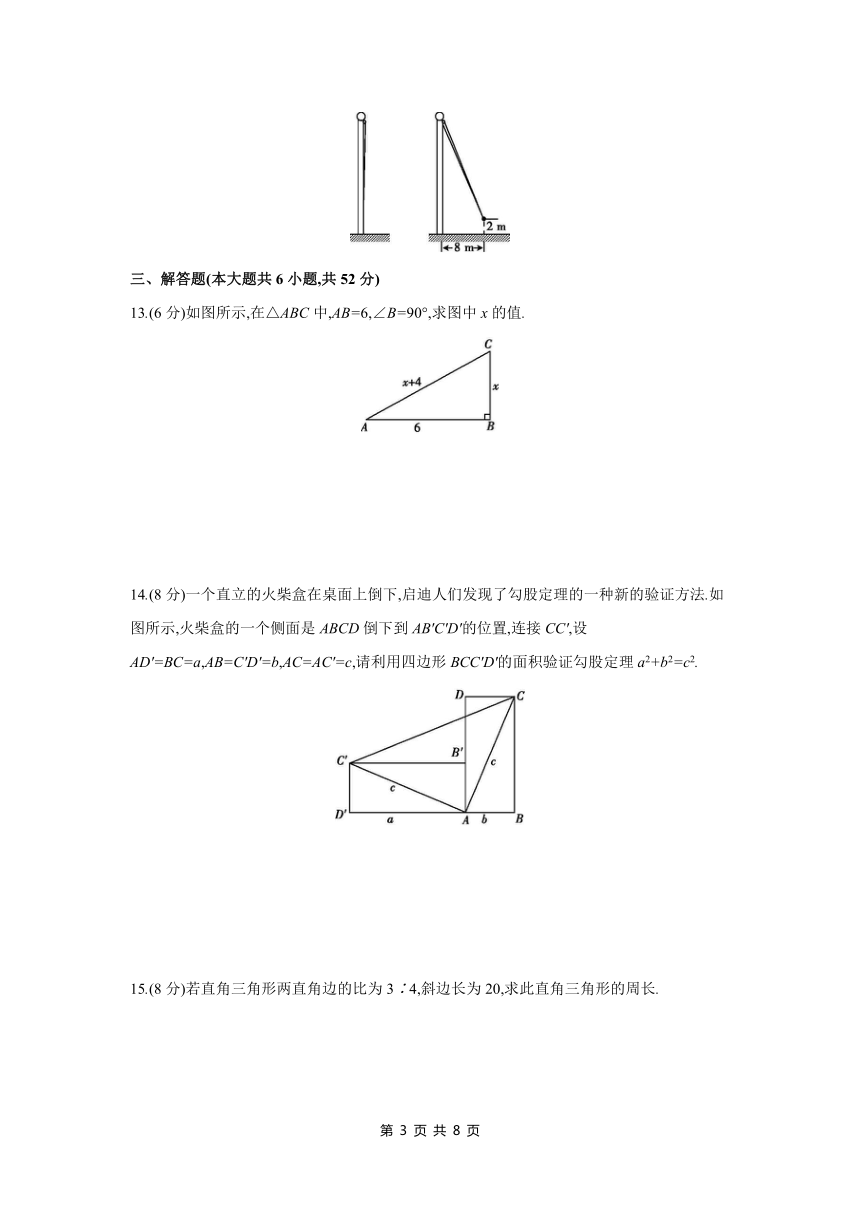
12.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为 m.
三、解答题(本大题共6小题,共52分)
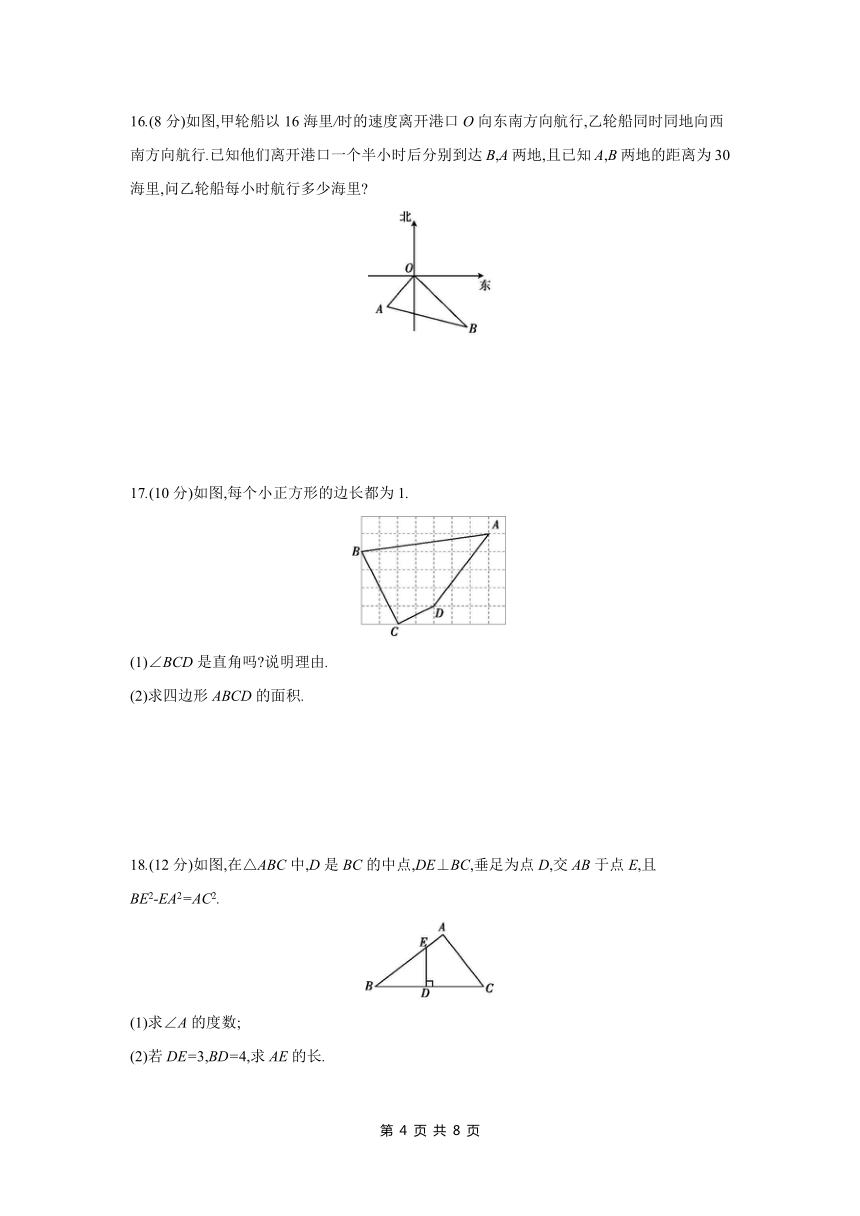
13.(6分)如图所示,在△ABC中,AB=6,∠B=90°,求图中x的值.
14.(8分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图所示,火柴盒的一个侧面是ABCD倒下到AB'C'D'的位置,连接CC',设AD'=BC=a,AB=C'D'=b,AC=AC'=c,请利用四边形BCC'D'的面积验证勾股定理a2+b2=c2.
15.(8分)若直角三角形两直角边的比为3∶4,斜边长为20,求此直角三角形的周长.
16.(8分)如图,甲轮船以16海里/时的速度离开港口O向东南方向航行,乙轮船同时同地向西南方向航行.已知他们离开港口一个半小时后分别到达B,A两地,且已知A,B两地的距离为30海里,问乙轮船每小时航行多少海里
17.(10分)如图,每个小正方形的边长都为1.
(1)∠BCD是直角吗 说明理由.
(2)求四边形ABCD的面积.
18.(12分)如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为点D,交AB于点E,且BE2-EA2=AC2.
(1)求∠A的度数;
(2)若DE=3,BD=4,求AE的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D D B C C A C A
1.D 【解析】根据勾股定理,可得AB===.
2.D 【解析】 因为32+42≠72,62+82≠122,72+122≠152,82+152=172,根据直角三角形两条边的平方和等于第三边的平方,可知8 cm,15 cm,17 cm这组木棒恰好能够做成直角三角形木架.
3.B 【解析】各选项的逆命题如下:A.对应角相等的两个三角形全等;B.等腰三角形的两边相等;C.如果两个数的绝对值相等,那么这两个数相等;D.若ab>0,则a<0,b<0.可知B选项的逆命题是真命题.
4.C 【解析】根据图形的面积等于各部分面积之和,化简整理得a2+b2=c2就能证明勾股定理,选项C不符合要求.
5.C 设正方形D的面积为x,∵正方形A,B,C的面积依次为2,4,3,∴2+4=x-3,解得x=9.
6.A 【解析】∵在Rt△OBC中,OC=1,OB=2,∴BC=,∴a=-+2.
7.C 【解析】 在Rt△ABE中,∵AE=6,BE=8,∴AB2=AE2+BE2=100,∴S阴影部分=S正方形ABCD-S△ABE=AB2-AE·BE=100-×6×8=76.
8.A 【解析】∵△AEF是由△ABE翻折而成,∴BE=EF=3,AB=AF,△CEF是直角三角形,∴CE=8-3=5,在Rt△CEF中,CF= = =4.设AB=x,在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6.
二、填空题
9 10 11 12
答案不唯一,如3,4,5;5,12,13 5 直角 17
10.5 【解析】设原来直角三角形的两直角边为a,b,斜边为c,则根据勾股定理,得a2+b2=c2,∴(5a)2+(5b)2=25(a2+b2)=25c2=(5c)2,即把直角三角形的两直角边均扩大到原来的5倍,则斜边扩大到原来的5倍.
11.直角 【解析】∵(a+b)2-c2=2ab,∴a2+b2=c2,∴此三角形为直角三角形.
12.17 【解析】如图,设旗杆高度为x,则AC=AD=x,AB=(x-2)m,BC=8 m,在Rt△ABC中,AB2+BC2=AC2,即(x-2)2+82=x2,解得x=17,即旗杆的高度为17 m.
三、解答题
13.解:在Rt△ABC中,根据勾股定理可得AB2+BC2=AC2,
∵AB=6,BC=x,AC=x+4,∴62+x2=(x+4)2, (3分)
整理,得36+x2=x2+8x+16,
解得x=,
∴x的值为. (6分)
14.解:S四边形BCC'D'=(a+b)(a+b)=(a+b)2,
S四边形BCC'D'=2×ab+c2, (4分)
∴(a+b)2=2×ab+c2,
即(a+b)2=2ab+c2,∴a2+b2=c2. (8分)
15.解:设直角三角形的两直角边分别是3x,4x,根据勾股定理,得9x2+16x2=400,
解得x=4或x=-4(舍去), (5分)
∴此直角三角形的周长为3x+4x+20=7×4+20=48. (8分)
16.解:∵甲轮船向东南方向航行,乙轮船向西南方向航行,∴AO⊥BO, (2分)
∵甲轮船以16海里/时的速度航行了一个半小时,
∴OB=16×1.5=24(海里), (4分)
∴在Rt△AOB中,AO2=AB2-OB2=302-242=324,即AO=18海里,
∴乙轮船每小时航行18÷1.5=12(海里). (8分)
17.解:(1)∠BCD是直角.
理由:如图,连接BD,由勾股定理,得BC2=22+42=20;DC2=12+22=5;BD2=32+42=25.
∵5+20=25,∴BC2+CD2=BD2,∴∠BCD是直角. (5分)
(2)∵BD2=25,AD2=25,AB2=50,∴BD2+AD2=AB2,∴∠BDA=90°,∴四边形ABCD的面积=BC·CD+BD·AD=××+×5×5=. (10分)
18.解:(1)如图,连接CE.
∵D是BC的中点,DE⊥BC,∴CE=BE.
∵BE2-EA2=AC2,∴CE2-EA2=AC2,即EA2+AC2=CE2,∴△ACE是直角三角形,
即∠A=90°. (6分)
(2)∵DE=3,BD=4,∴BE=CE=5,∴AC2=EC2-AE2=25-EA2,
∵BD=4,∴BC=2BD=8,
在Rt△BAC中,由勾股定理,得BC2-BA2=AC2,
∴64-(5+AE)2=25-EA2,解得AE=. (12分)
基础过关测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.如图,在△ABC中,∠C=90°,若BC=3,AC=5,则AB= ( )
A.4 B.6 C.8 D.
2.小明想做一个直角三角形的木架,以下四组木棒中,能够刚好做成直角三角形木架的是 ( )
A.3 cm,4 cm,7 cm B.6 cm,8 cm,12 cm
C.7 cm,12 cm,15 cm D.8 cm,15 cm,17 cm
3.下列各命题的逆命题是真命题的是 ( )
A.全等三角形的对应角相等
B.有两边相等的三角形是等腰三角形
C.如果两个数相等,那么这两个数的绝对值相等
D.若a<0,b<0,则ab>0
4.下面各图中,不能证明勾股定理正确性的是 ( )
5.如图,图中所有四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次为2,4,3,则正方形D的面积为 ( )
A.7 B.8 C.9 D.10
6.如图,在Rt△OBC中,OC=1,OB=2,数轴上点A所表示的数为a,则a的值是 ( )
A.-+2 B.--2 C.-2 D.-
7.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是
( )
A.48 B.60 C.76 D.80
8.如图,在长方形纸片ABCD中,已知BC=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.6 B.5 C.4 D.3
二、填空题(每小题4分,共16分)
9.写出一组你喜欢的勾股数: .
10.若直角三角形的两直角边均扩大到原来的5倍,则斜边扩大到原来的 倍.
11.若三角形的三边长为a,b,c,且满足等式(a+b)2-c2=2ab,则此三角形为 三角形.(填“直角”“等腰”或“等边”)
12.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为 m.
三、解答题(本大题共6小题,共52分)
13.(6分)如图所示,在△ABC中,AB=6,∠B=90°,求图中x的值.
14.(8分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图所示,火柴盒的一个侧面是ABCD倒下到AB'C'D'的位置,连接CC',设AD'=BC=a,AB=C'D'=b,AC=AC'=c,请利用四边形BCC'D'的面积验证勾股定理a2+b2=c2.
15.(8分)若直角三角形两直角边的比为3∶4,斜边长为20,求此直角三角形的周长.
16.(8分)如图,甲轮船以16海里/时的速度离开港口O向东南方向航行,乙轮船同时同地向西南方向航行.已知他们离开港口一个半小时后分别到达B,A两地,且已知A,B两地的距离为30海里,问乙轮船每小时航行多少海里
17.(10分)如图,每个小正方形的边长都为1.
(1)∠BCD是直角吗 说明理由.
(2)求四边形ABCD的面积.
18.(12分)如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为点D,交AB于点E,且BE2-EA2=AC2.
(1)求∠A的度数;
(2)若DE=3,BD=4,求AE的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D D B C C A C A
1.D 【解析】根据勾股定理,可得AB===.
2.D 【解析】 因为32+42≠72,62+82≠122,72+122≠152,82+152=172,根据直角三角形两条边的平方和等于第三边的平方,可知8 cm,15 cm,17 cm这组木棒恰好能够做成直角三角形木架.
3.B 【解析】各选项的逆命题如下:A.对应角相等的两个三角形全等;B.等腰三角形的两边相等;C.如果两个数的绝对值相等,那么这两个数相等;D.若ab>0,则a<0,b<0.可知B选项的逆命题是真命题.
4.C 【解析】根据图形的面积等于各部分面积之和,化简整理得a2+b2=c2就能证明勾股定理,选项C不符合要求.
5.C 设正方形D的面积为x,∵正方形A,B,C的面积依次为2,4,3,∴2+4=x-3,解得x=9.
6.A 【解析】∵在Rt△OBC中,OC=1,OB=2,∴BC=,∴a=-+2.
7.C 【解析】 在Rt△ABE中,∵AE=6,BE=8,∴AB2=AE2+BE2=100,∴S阴影部分=S正方形ABCD-S△ABE=AB2-AE·BE=100-×6×8=76.
8.A 【解析】∵△AEF是由△ABE翻折而成,∴BE=EF=3,AB=AF,△CEF是直角三角形,∴CE=8-3=5,在Rt△CEF中,CF= = =4.设AB=x,在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6.
二、填空题
9 10 11 12
答案不唯一,如3,4,5;5,12,13 5 直角 17
10.5 【解析】设原来直角三角形的两直角边为a,b,斜边为c,则根据勾股定理,得a2+b2=c2,∴(5a)2+(5b)2=25(a2+b2)=25c2=(5c)2,即把直角三角形的两直角边均扩大到原来的5倍,则斜边扩大到原来的5倍.
11.直角 【解析】∵(a+b)2-c2=2ab,∴a2+b2=c2,∴此三角形为直角三角形.
12.17 【解析】如图,设旗杆高度为x,则AC=AD=x,AB=(x-2)m,BC=8 m,在Rt△ABC中,AB2+BC2=AC2,即(x-2)2+82=x2,解得x=17,即旗杆的高度为17 m.
三、解答题
13.解:在Rt△ABC中,根据勾股定理可得AB2+BC2=AC2,
∵AB=6,BC=x,AC=x+4,∴62+x2=(x+4)2, (3分)
整理,得36+x2=x2+8x+16,
解得x=,
∴x的值为. (6分)
14.解:S四边形BCC'D'=(a+b)(a+b)=(a+b)2,
S四边形BCC'D'=2×ab+c2, (4分)
∴(a+b)2=2×ab+c2,
即(a+b)2=2ab+c2,∴a2+b2=c2. (8分)
15.解:设直角三角形的两直角边分别是3x,4x,根据勾股定理,得9x2+16x2=400,
解得x=4或x=-4(舍去), (5分)
∴此直角三角形的周长为3x+4x+20=7×4+20=48. (8分)
16.解:∵甲轮船向东南方向航行,乙轮船向西南方向航行,∴AO⊥BO, (2分)
∵甲轮船以16海里/时的速度航行了一个半小时,
∴OB=16×1.5=24(海里), (4分)
∴在Rt△AOB中,AO2=AB2-OB2=302-242=324,即AO=18海里,
∴乙轮船每小时航行18÷1.5=12(海里). (8分)
17.解:(1)∠BCD是直角.
理由:如图,连接BD,由勾股定理,得BC2=22+42=20;DC2=12+22=5;BD2=32+42=25.
∵5+20=25,∴BC2+CD2=BD2,∴∠BCD是直角. (5分)
(2)∵BD2=25,AD2=25,AB2=50,∴BD2+AD2=AB2,∴∠BDA=90°,∴四边形ABCD的面积=BC·CD+BD·AD=××+×5×5=. (10分)
18.解:(1)如图,连接CE.
∵D是BC的中点,DE⊥BC,∴CE=BE.
∵BE2-EA2=AC2,∴CE2-EA2=AC2,即EA2+AC2=CE2,∴△ACE是直角三角形,
即∠A=90°. (6分)
(2)∵DE=3,BD=4,∴BE=CE=5,∴AC2=EC2-AE2=25-EA2,
∵BD=4,∴BC=2BD=8,
在Rt△BAC中,由勾股定理,得BC2-BA2=AC2,
∴64-(5+AE)2=25-EA2,解得AE=. (12分)
