第十七章 勾股定理 能力提优测试卷(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十七章 勾股定理 能力提优测试卷(含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 258.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:22:25 | ||
图片预览


文档简介
第十七章 勾股定理
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.点A(6,8)到原点O的距离为 ( )
A.2 B.6 C.8 D.10
2.在Rt△ABC中,∠BAC=90°,AB=9,AC=12,AD是BC边上的高,则AD的长为 ( )
A. B. C. D.
3.如图,在正方形网格中,每一小格的边长为1,网格内有△PAB,则∠PAB+∠PBA的度数是 ( )
A.30° B.45° C.50° D.60°
4.若△ABC的三边a,b,c满足(a-b)2+=0,则△ABC是 ( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等腰三角形或直角三角形
5.如图,一根长为5米的竹竿AB斜靠在一竖直的墙AO上,这时AO为4米,如果竹竿的顶端A沿墙下滑1米,那么竹竿底端B外移的距离BD ( )
A.等于1米 B.大于1米
C.小于1米 D.以上都不对
6.如图,一艘轮船和一艘渔船同时沿各自的航向从港口O出发,轮船从港口O沿北偏西20°的方向航行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M,N两点相距100海里,则∠NOF的度数为 ( )
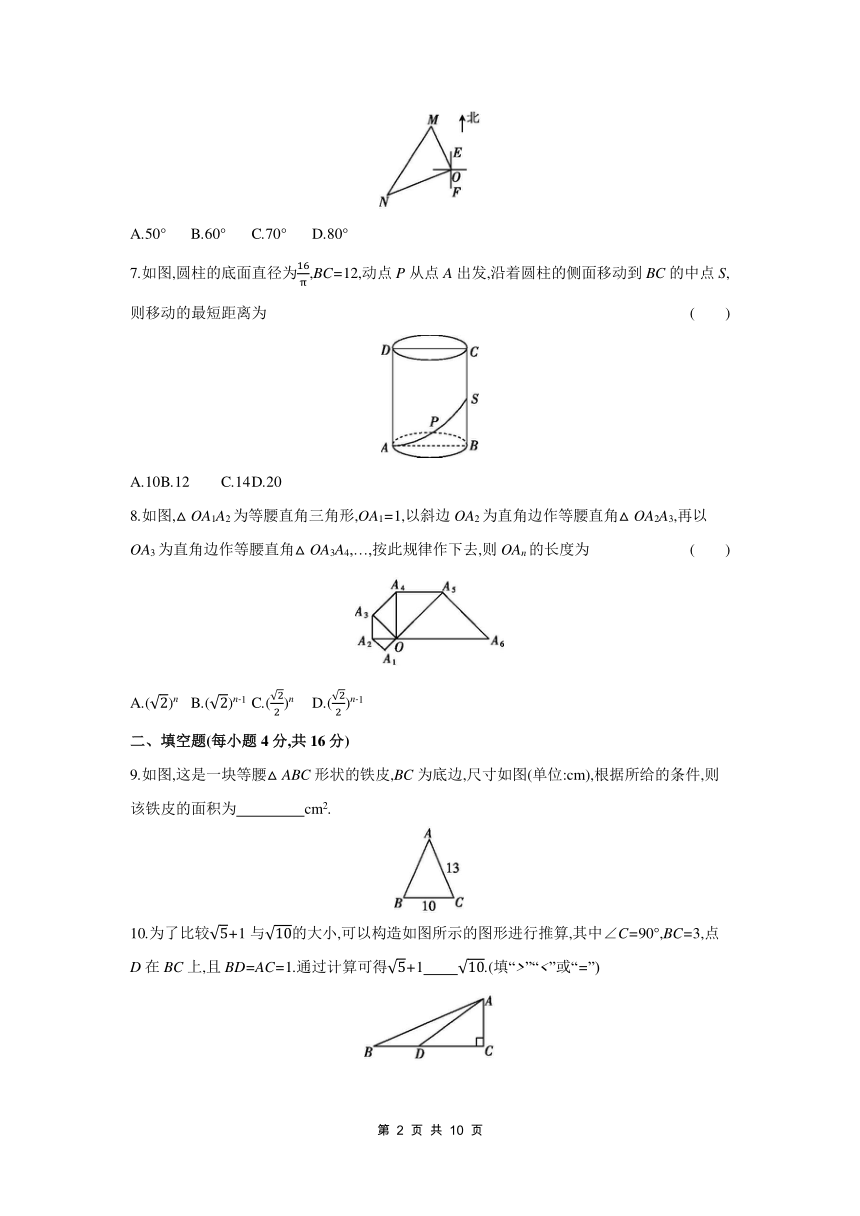
A.50° B.60° C.70° D.80°
7.如图,圆柱的底面直径为,BC=12,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,则移动的最短距离为 ( )
A.10 B.12 C.14 D.20
8.如图,△OA1A2为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角△OA2A3,再以OA3为直角边作等腰直角△OA3A4,…,按此规律作下去,则OAn的长度为 ( )
A.()n B.()n-1 C.()n D.()n-1
二、填空题(每小题4分,共16分)
9.如图,这是一块等腰△ABC形状的铁皮,BC为底边,尺寸如图(单位:cm),根据所给的条件,则该铁皮的面积为 cm2.
10.为了比较+1与的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,点D在BC上,且BD=AC=1.通过计算可得+1 .(填“>”“<”或“=”)
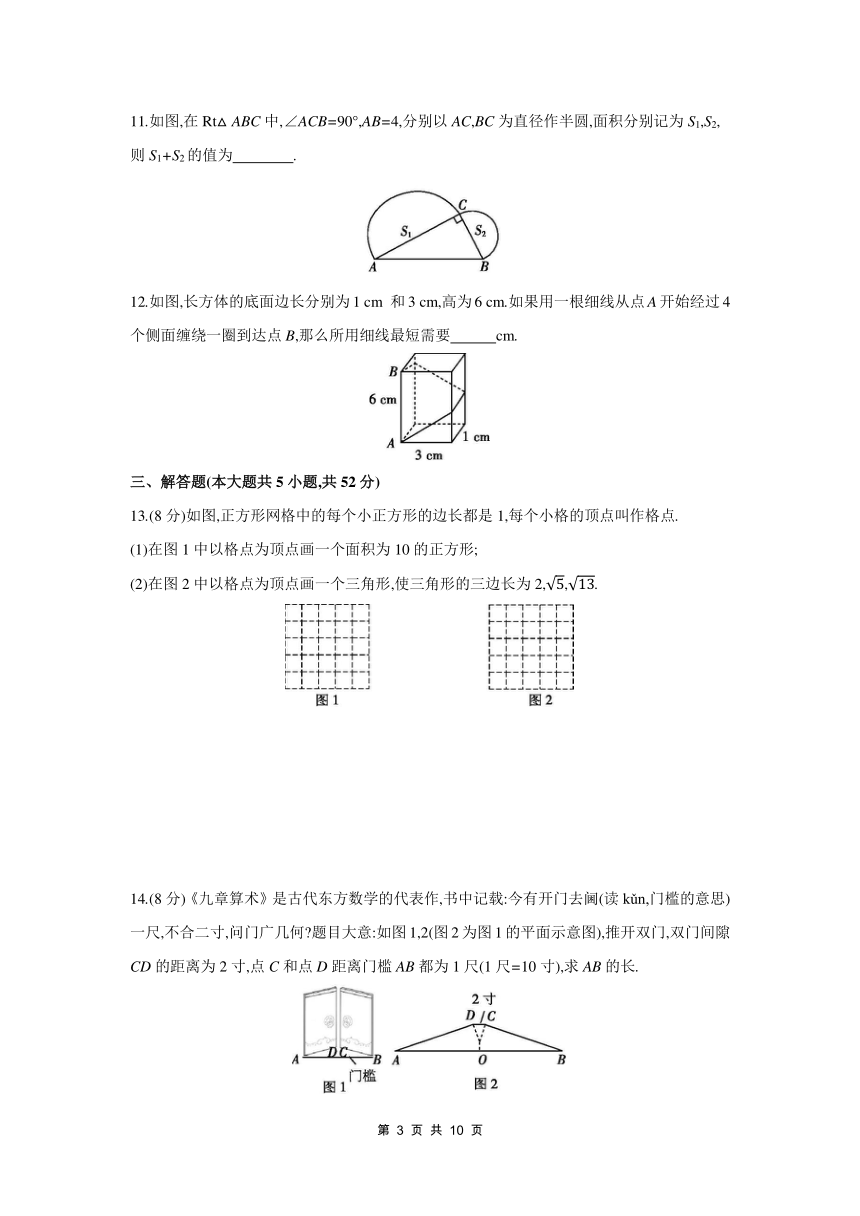
11.如图,在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值为 .
12.如图,长方体的底面边长分别为1 cm 和3 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm.
三、解答题(本大题共5小题,共52分)
13.(8分)如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫作格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形的三边长为2,,.
14.(8分)《九章算术》是古代东方数学的代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意:如图1,2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),求AB的长.
15.(10分)如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4,CD=8.
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.
16.(12分)观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;a,b,c.
根据你发现的规律,回答下列问题:
(1)当a=19时,求b,c的值;
(2)当a=2n+1时,求b,c的值;
(3)用(2)中的结论判断15,111,112是否为一组勾股数,并说明理由.
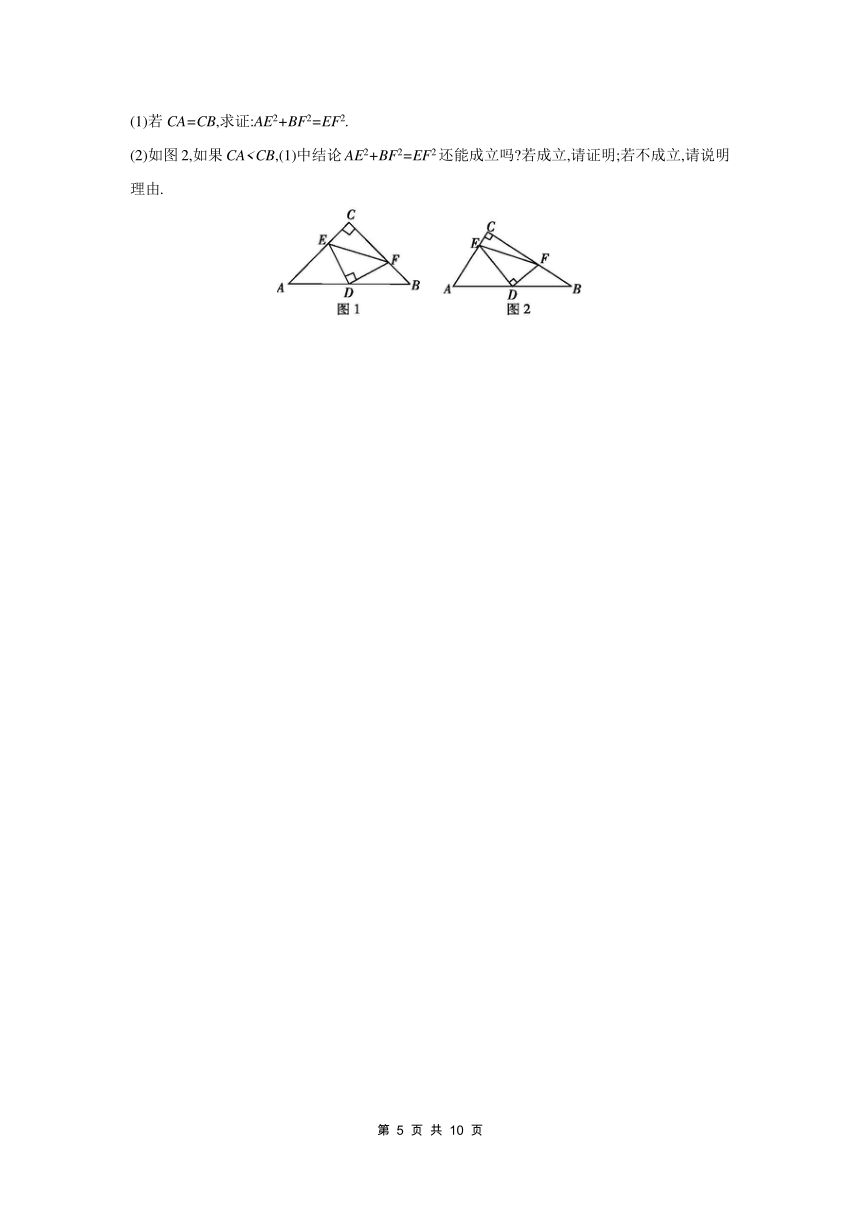
17.(14分)如图1,在Rt△ABC中,∠ACB=90°,D为AB的中点,DE,DF分别交AC于点E,交BC于点F,且DE⊥DF.
(1)若CA=CB,求证:AE2+BF2=EF2.
(2)如图2,如果CA参考答案
一、选择题
1 2 3 4 5 6 7 8
D A B B A C A B
1.D 【解析】由勾股定理,得OA==10.
2.A 【解析】BC==15,由三角形的面积恒等得AD===.
3.B 【解析】延长AP到C,连接BC,如图所示,由图可知,∠CPB=∠PAB+∠PBA,PC=,BC=,PB=,∴BC2+PC2=PB2,CP=CB.∴△BCP是等腰直角三角形,∴∠CPB=∠PAB+∠PBA=45°.
4.B 【解析】根据数的平方与二次根式的非负性,得a=b,a2+b2=c2,由此可知△ABC是等腰直角三角形.
5.A 【解析】在Rt△AOB中,OB==3;在Rt△COD中,OD==4,∴BD=OD-OB=1米.
6.C 【解析】由题意可知OM=60海里,ON=80海里,MN=100海里,∴OM2+ON2=MN2,∴△MNF是直角三角形,∠MON=90°,∴∠NOF=180°-∠MON-∠MOE=180°-90°-20°=70°.
7.A 【解析】如图,AB=××π=8,BS=BC=6,所以AS=10.
8.B 【解析】∵△OA1A2为等腰直角三角形,OA1=1,∴OA2=;∵△OA2A3为等腰直角三角形,∴OA3=2=()2;∵△OA3A4为等腰直角三角形,∴OA4=2=()3.∵△OA4A5为等腰直角三角形,∴OA5=4=()4,…,∴OAn的长度为()n-1.
二、填空题
9 10 11 12
60 > 2π 10
9.60 【解析】过点A作AD⊥BC于点D,则BD=CD=5,AD==12,∴S△ABC=BC×AD=60(cm2).
10.> 【解析】由题意可知CD=BC-BD=2,AD==,AB==,∴BD+AD=+1.在△ABD中,由三角形的三边关系,得AD+BD>AB,∴+1>.
11.2π 【解析】设S1的半径为R,S2的半径为r.由勾股定理得(2R)2+(2r)2=16,解得R2+r2=4,则S1+S2=πR2+πr2=π(R2+r2)=2π.
12.10 【解析】如图,将长方体展开,连接AB',因为AA'=1+3+1+3=8(cm),A'B'=6 cm,根据两点之间线段最短,AB'2=82+62=100,即AB'=10 cm.
三、解答题
13.解: (1)如图1所示的正方形的边长是,面积是10; (4分)
(2)如图2所示的三角形的边长分别为2,,. (8分)
14.解:如图所示,过点D作DE⊥AB于点E, (1分)
由题意可知OA=OB=AD=BC,故可设OA=OB=AD=BC=r,则AB=2r,DE=10寸,OE=CD=1寸,AE=(r-1)寸. (4分)
在Rt△ADE中,由勾股定理,得AE2+DE2=AD2,即(r-1)2+102=r2,解得r=50.5,
则2r=101,∴AB=101寸. (8分)
15.解:(1)如图,连接BD,∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,DB=4,
∵42+82=(4)2,
∴DB2+CD2=BC2,则△BCD是直角三角形,
∴∠BDC=90°,
∴∠ADC=60°+90°=150°. (5分)
(2)过点B作BE⊥AD,则AE=2,BE==2.
∴S四边形ABCD=AD·EB+DB·CD=×4×2+×4×8=4+16. (10分)
16.解: (1)观察可得给出的勾股数中,斜边与较大直角边的差是1,即c-b=1.
∵a=19,a2+b2=c2,则192+b2=(b+1)2,
解得b=180,则c=181. (4分)
(2)由题意可知c-b=1.
∵(2n+1)2+b2=c2,
∴c2-b2=(2n+1)2,
因式分解,得(b+c)(c-b)=(2n+1)2,
代入c-b=1,得 b+c=(2n+1)2,
又c=b+1,∴2b+1=(2n+1)2,
∴b=2n2+2n,c=2n2+2n+1. (8分)
(3)由(2)知2n+1,2n2+2n,2n2+2n+1为一组勾股数,
当n=7时,2n+1=15,112-111=1,
但2n2+2n=112≠111,
∴15,111,112不是一组勾股数. (12分)
17.解:(1)证明:如图1,过点A作AM∥BC,交FD延长线于点M,连接EM.
∵AM∥BC,
∴∠MAE=∠ACB=90°,∠MAD=∠B.
∵AD=BD,∠ADM=∠BDF,
∴△ADM≌△BDF, (3分)
∴AM=BF,MD=DF.
又∵DE⊥DF,∴EF=EM.
∴AE2+BF2=AE2+AM2=EM2=EF2. (7分)
(2)成立. (8分)
证明:如图2,延长FD至M,使DM=DF,连接AM,EM.
∵AD=BD,∠ADM=∠BDF,
∴△ADM≌△BDF. (10分)
∴AM=BF,∠MAD=∠B,
∴AM∥BC,∴∠MAE=∠ACB=90°. (12分)
又∵DE⊥DF,MD=FD,∴EF=EM.
∴AE2+BF2=AE2+AM2=EM2=EF2. (14分)
能力提优测试卷
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.点A(6,8)到原点O的距离为 ( )
A.2 B.6 C.8 D.10
2.在Rt△ABC中,∠BAC=90°,AB=9,AC=12,AD是BC边上的高,则AD的长为 ( )
A. B. C. D.
3.如图,在正方形网格中,每一小格的边长为1,网格内有△PAB,则∠PAB+∠PBA的度数是 ( )
A.30° B.45° C.50° D.60°
4.若△ABC的三边a,b,c满足(a-b)2+=0,则△ABC是 ( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等腰三角形或直角三角形
5.如图,一根长为5米的竹竿AB斜靠在一竖直的墙AO上,这时AO为4米,如果竹竿的顶端A沿墙下滑1米,那么竹竿底端B外移的距离BD ( )
A.等于1米 B.大于1米
C.小于1米 D.以上都不对
6.如图,一艘轮船和一艘渔船同时沿各自的航向从港口O出发,轮船从港口O沿北偏西20°的方向航行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M,N两点相距100海里,则∠NOF的度数为 ( )
A.50° B.60° C.70° D.80°
7.如图,圆柱的底面直径为,BC=12,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,则移动的最短距离为 ( )
A.10 B.12 C.14 D.20
8.如图,△OA1A2为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角△OA2A3,再以OA3为直角边作等腰直角△OA3A4,…,按此规律作下去,则OAn的长度为 ( )
A.()n B.()n-1 C.()n D.()n-1
二、填空题(每小题4分,共16分)
9.如图,这是一块等腰△ABC形状的铁皮,BC为底边,尺寸如图(单位:cm),根据所给的条件,则该铁皮的面积为 cm2.
10.为了比较+1与的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,点D在BC上,且BD=AC=1.通过计算可得+1 .(填“>”“<”或“=”)
11.如图,在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值为 .
12.如图,长方体的底面边长分别为1 cm 和3 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm.
三、解答题(本大题共5小题,共52分)
13.(8分)如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫作格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形的三边长为2,,.
14.(8分)《九章算术》是古代东方数学的代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意:如图1,2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),求AB的长.
15.(10分)如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4,CD=8.
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.
16.(12分)观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;a,b,c.
根据你发现的规律,回答下列问题:
(1)当a=19时,求b,c的值;
(2)当a=2n+1时,求b,c的值;
(3)用(2)中的结论判断15,111,112是否为一组勾股数,并说明理由.
17.(14分)如图1,在Rt△ABC中,∠ACB=90°,D为AB的中点,DE,DF分别交AC于点E,交BC于点F,且DE⊥DF.
(1)若CA=CB,求证:AE2+BF2=EF2.
(2)如图2,如果CA
一、选择题
1 2 3 4 5 6 7 8
D A B B A C A B
1.D 【解析】由勾股定理,得OA==10.
2.A 【解析】BC==15,由三角形的面积恒等得AD===.
3.B 【解析】延长AP到C,连接BC,如图所示,由图可知,∠CPB=∠PAB+∠PBA,PC=,BC=,PB=,∴BC2+PC2=PB2,CP=CB.∴△BCP是等腰直角三角形,∴∠CPB=∠PAB+∠PBA=45°.
4.B 【解析】根据数的平方与二次根式的非负性,得a=b,a2+b2=c2,由此可知△ABC是等腰直角三角形.
5.A 【解析】在Rt△AOB中,OB==3;在Rt△COD中,OD==4,∴BD=OD-OB=1米.
6.C 【解析】由题意可知OM=60海里,ON=80海里,MN=100海里,∴OM2+ON2=MN2,∴△MNF是直角三角形,∠MON=90°,∴∠NOF=180°-∠MON-∠MOE=180°-90°-20°=70°.
7.A 【解析】如图,AB=××π=8,BS=BC=6,所以AS=10.
8.B 【解析】∵△OA1A2为等腰直角三角形,OA1=1,∴OA2=;∵△OA2A3为等腰直角三角形,∴OA3=2=()2;∵△OA3A4为等腰直角三角形,∴OA4=2=()3.∵△OA4A5为等腰直角三角形,∴OA5=4=()4,…,∴OAn的长度为()n-1.
二、填空题
9 10 11 12
60 > 2π 10
9.60 【解析】过点A作AD⊥BC于点D,则BD=CD=5,AD==12,∴S△ABC=BC×AD=60(cm2).
10.> 【解析】由题意可知CD=BC-BD=2,AD==,AB==,∴BD+AD=+1.在△ABD中,由三角形的三边关系,得AD+BD>AB,∴+1>.
11.2π 【解析】设S1的半径为R,S2的半径为r.由勾股定理得(2R)2+(2r)2=16,解得R2+r2=4,则S1+S2=πR2+πr2=π(R2+r2)=2π.
12.10 【解析】如图,将长方体展开,连接AB',因为AA'=1+3+1+3=8(cm),A'B'=6 cm,根据两点之间线段最短,AB'2=82+62=100,即AB'=10 cm.
三、解答题
13.解: (1)如图1所示的正方形的边长是,面积是10; (4分)
(2)如图2所示的三角形的边长分别为2,,. (8分)
14.解:如图所示,过点D作DE⊥AB于点E, (1分)
由题意可知OA=OB=AD=BC,故可设OA=OB=AD=BC=r,则AB=2r,DE=10寸,OE=CD=1寸,AE=(r-1)寸. (4分)
在Rt△ADE中,由勾股定理,得AE2+DE2=AD2,即(r-1)2+102=r2,解得r=50.5,
则2r=101,∴AB=101寸. (8分)
15.解:(1)如图,连接BD,∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,DB=4,
∵42+82=(4)2,
∴DB2+CD2=BC2,则△BCD是直角三角形,
∴∠BDC=90°,
∴∠ADC=60°+90°=150°. (5分)
(2)过点B作BE⊥AD,则AE=2,BE==2.
∴S四边形ABCD=AD·EB+DB·CD=×4×2+×4×8=4+16. (10分)
16.解: (1)观察可得给出的勾股数中,斜边与较大直角边的差是1,即c-b=1.
∵a=19,a2+b2=c2,则192+b2=(b+1)2,
解得b=180,则c=181. (4分)
(2)由题意可知c-b=1.
∵(2n+1)2+b2=c2,
∴c2-b2=(2n+1)2,
因式分解,得(b+c)(c-b)=(2n+1)2,
代入c-b=1,得 b+c=(2n+1)2,
又c=b+1,∴2b+1=(2n+1)2,
∴b=2n2+2n,c=2n2+2n+1. (8分)
(3)由(2)知2n+1,2n2+2n,2n2+2n+1为一组勾股数,
当n=7时,2n+1=15,112-111=1,
但2n2+2n=112≠111,
∴15,111,112不是一组勾股数. (12分)
17.解:(1)证明:如图1,过点A作AM∥BC,交FD延长线于点M,连接EM.
∵AM∥BC,
∴∠MAE=∠ACB=90°,∠MAD=∠B.
∵AD=BD,∠ADM=∠BDF,
∴△ADM≌△BDF, (3分)
∴AM=BF,MD=DF.
又∵DE⊥DF,∴EF=EM.
∴AE2+BF2=AE2+AM2=EM2=EF2. (7分)
(2)成立. (8分)
证明:如图2,延长FD至M,使DM=DF,连接AM,EM.
∵AD=BD,∠ADM=∠BDF,
∴△ADM≌△BDF. (10分)
∴AM=BF,∠MAD=∠B,
∴AM∥BC,∴∠MAE=∠ACB=90°. (12分)
又∵DE⊥DF,MD=FD,∴EF=EM.
∴AE2+BF2=AE2+AM2=EM2=EF2. (14分)
