期末闯关测试卷(二) (含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 期末闯关测试卷(二) (含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 241.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:22:42 | ||
图片预览




文档简介
期末测试卷(二)
时间:90分钟 满分:120分 考试范围:下册全部内容
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共30分)
1.下列二次根式中,是最简二次根式的是 ( )
A. B. C. D.
2.为筹备班级的初中毕业联欢会,班委会经过讨论决定在苹果、橘子、香蕉、梨四种水果中选出一种购买,班长对全班学生爱吃哪种水果做了调查,则最终在决定购买哪种水果时,下面的调查数据中最值得关注的是 ( )
A.众数 B.平均数 C.中位数 D.方差
3.如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是 ( )
A.16 B.20 C.30 D.60
4.如图,数轴上点A对应的数是-1,点C对应的数是-3,BC⊥AC,垂足为点C,且BC=1,以点A为圆心,AB的长为半径画弧,交数轴于点D,则点D表示的数为( )
A.-1 B. C.-1 D.
5.若点P(-2,4)关于y轴的对称点在一次函数y=x+b的图象上,则b的值为( )
A.-3 B.3 C.-2 D.2
6.数据8,7,6,7,6,5,4,5,8,6的中位数是 ( )
A.8 B.7 C.6 D.5
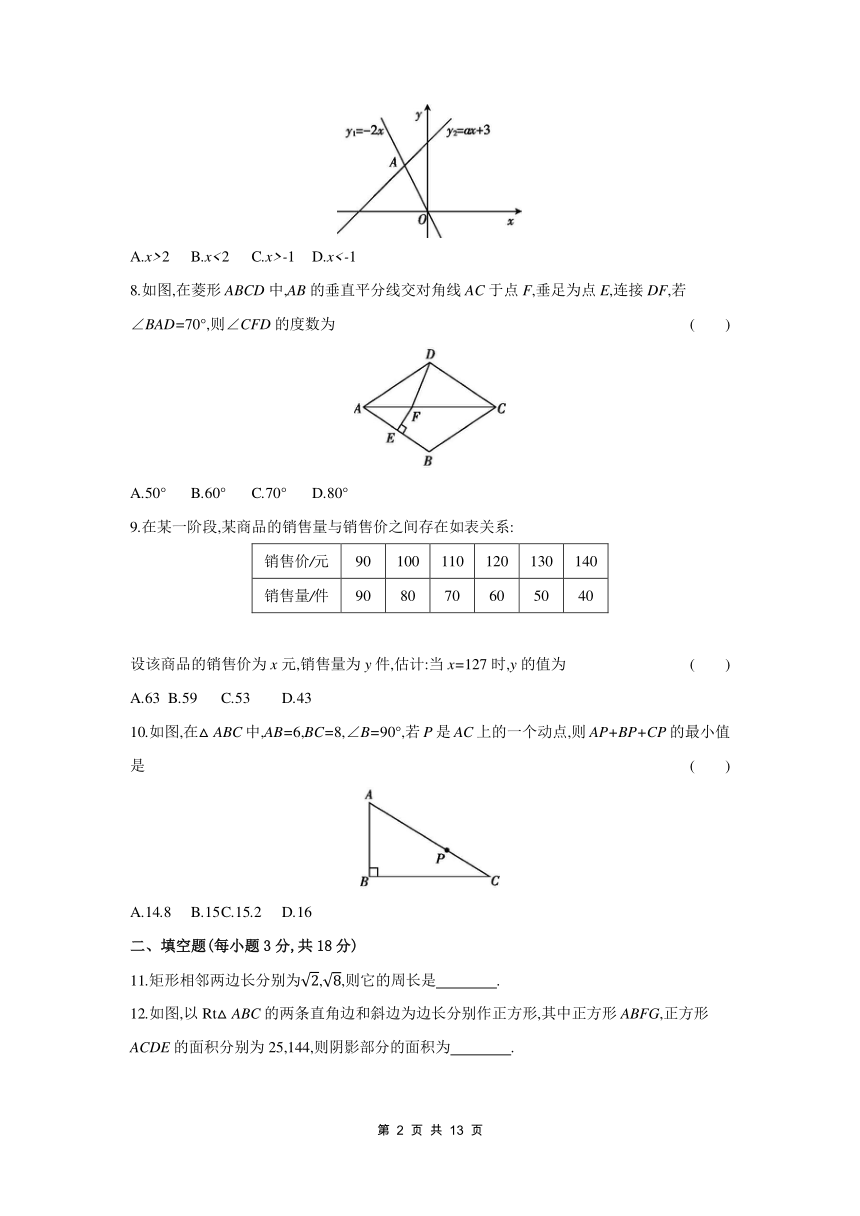
7.如图,函数y1=-2x和y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是 ( )
A.x>2 B.x<2 C.x>-1 D.x<-1
8.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,若∠BAD=70°,则∠CFD的度数为 ( )
A.50° B.60° C.70° D.80°
9.在某一阶段,某商品的销售量与销售价之间存在如表关系:
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
设该商品的销售价为x元,销售量为y件,估计:当x=127时,y的值为 ( )
A.63 B.59 C.53 D.43
10.如图,在△ABC中,AB=6,BC=8,∠B=90°,若P是AC上的一个动点,则AP+BP+CP的最小值是 ( )
A.14.8 B.15 C.15.2 D.16
二、填空题(每小题3分,共18分)
11.矩形相邻两边长分别为,,则它的周长是 .
12.如图,以Rt△ABC的两条直角边和斜边为边长分别作正方形,其中正方形ABFG,正方形ACDE的面积分别为25,144,则阴影部分的面积为 .
13.某灯泡厂为测量一批灯泡的使用寿命,从中抽查了100只灯泡,它们的使用寿命如下表所示:
使用寿命x/h 60≤x<100 100≤x<140 140≤x<180
灯泡只数 30 30 40
则这批灯泡的平均使用寿命是 h.
14.如果某公司一销售人员的个人月收入y与其每月的销售量x成一次函数(如图所示),那么此销售人员的销售量在4千件时的月收入是 元.
15.如图,将一组邻边长分别为5和12的两个矩形ABCD和矩形AEFG拼成“L”形图案,则线段CF的长为 .
16.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB于点E,点F,G分别是AD,BC的中点,连接CF,EF,FG,EG,下列四种说法:①CE⊥FG;②四边形ABGF是菱形;③BC=2EG;④∠DFC=∠EFG.其中正确的是 .(填序号)
三、解答题(本大题共9小题,共72分)
17.(6分)计算:(1)+-;(2)(1+-)(1-+).
18.(6分)如图,等边△ABC的边长是4,D,E 分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD,EF.
(1)求证:DE=CF.
(2)求EF的长.
19.(6分)某销售公司有营销人员14人,销售部为了制定某种品牌的净水器的月销售量定额,统计了这14人在某月的销售量如下表:
销售台数 20 18 14 9 7 4
人数 1 1 2 5 3 2
(1)这14位销售员该月销售量的平均数、众数和中位数各是多少台
(2)销售部经理把每位销售员每月销售量定为10台,你认为是否合理,为什么 如果不合理,请你设计一个比较合理的销售定额,并说明理由.
20.(6分)函数y=kx+b的图象如图所示,利用函数图象解答下列问题:
(1)解方程kx+b=1.5;
(2)解不等式kx+b<0;
(3)解不等式组0.521.(8分)某玉米种子的价格为60元/千克,如果一次性购买5千克以上的种子,超过5千克部分的种子的价格打8折.
(1)根据题意,补充下表:
购买种子的质量/千克 3 4 5 6 …
付款金额/元 180 300 …
(2)设购买种子的质量为x(x>5)千克,付款金额为y元,求y与x的函数关系式;
(3)若王伯伯一次性购买该种子花了540元,求他购买种子的质量.
22.(8分)“儿童散学归来早,忙趁东风放纸鸢.”如图,小明站在C处,同时小亮在斜坡的D处,DG⊥GB且DG=10米,CG=60米,CE⊥GB.(不考虑两人身高,点G,C,B在同一水平线上)
(1)求小明与小亮之间的距离CD.(结果保留根号)
(2)若风筝A在小明的北偏东45°方向上,且高度AB为60米,AB⊥GB,求此时风筝A到小亮的距离AD.
23.(10分)如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD中点,FH=1,求菱形ABCD的周长.
24.(10分)某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费.如图所示,图中表示了公司每月付给推销员推销费的两种方案,根据图中所示信息解答下列问题:
(1)写出y1与y2对应的二元一次方程组;(不考虑取值范围)
(2)请直接写出(1)中方程组的解,并解释(300,6000)的含义;
(3)解释图中表示的两种方案是如何付推销费的;
(4)如果你是推销员,应如何选择付费方案
25.(12分)综合与实践:如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等,OA1交BC于点E,OC1交CD于点F.
知识初探:求证:OE=OF.
探究计算:若AB=2,求四边形OECF的面积.
探究拓展:如图2,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC,若AC=4,求四边形ABCD的面积.
图1 图2
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D A B A B C D C C A
2.A 【解析】爱吃的水果人数越多,班长就应多买,而众数反映的就是.
3.B 【解析】∵DE平分∠ADC,∴∠ADE=∠CDE,在 ABCD中,∴AD∥BC,∴∠ADE=∠CED,∴∠CDE=∠CED,∴CE=CD,在 ABCD中,AD=6,BE=2,∴AD=BC=6,∴CE=BC-BE=6-2=4,∴CD=AB=4,∴ ABCD的周长=6+6+4+4=20.
4.A 【解析】∵BC⊥AC,∴∠BCA=90°,∴AB===,∵以A为圆心,AB为半径画弧,交数轴于点D,∴AD=AB=,∴点D表示的数是-1.
5.B 【解析】∵点P(-2,4)关于y轴的对称点为(2,4),∴把(2,4)代入一次函数y=x+b,得2×+b=4,解得b=3.
6.C 【解析】把这组数据从小到大排序为4,5,5,6,6,6,7,7,8,8,所以中位数是=6.
7.D 【解析】∵函数y1=-2x的图象经过点A(m,2),∴-2m=2,解得m=-1,∴A(-1,2),观察两个函数图象可知,当函数y1=-2x在函数y2=ax+3的图象上方时,x<-1,即不等式-2x>ax+3的解集为x<-1.
8.C 【解析】如图所示,连接BF,∵四边形ABCD是菱形,∴∠BAC=∠BAD=×70°=35°,∠BCF=∠DCF=∠BAC,BC=DC,∠ABC=180°-∠BAD=180°-70°=110°,∵EF是线段AB的垂直平分线,∴AF=BF,∴∠DCF=∠ABF=∠BAC=35°,∴∠CBF=∠ABC-∠ABF=110°-35°=75°,在△BCF和△DCF中,,∴△BCF≌△DCF,∴∠CDF=∠CBF=75°,∴∠CFD=180°-∠CDF-∠DCF=180°-75°-35°=70°.
9.C 【解析】由图表可以看出y与x符合一次函数关系,设y=kx+b(k≠0),把x=90,y=90和x=100,y=80代入得,解得,则y=-x+180,当x=127时,y=-127+180=53.
10.A 【解析】∵∠B=90°,AB=6,BC=8,∴AC===10,∵AP+BP+PC=BP+AC=BP+10,根据垂线段最短可知,当BP⊥AC时,BP的值最小,最小值BP===4.8,∴AP+BP+CP的最小值=10+4.8=14.8.
二、填空题
11 12 13 14 15 16
6 139 124 1100 13 ①②③④
11.6 【解析】矩形的周长是2×(+)=2×(+2)=6.
12.139 【解析】根据题意知AB2=25,AC2=144,∴AB=5,AC=12,BC===13,∴S阴影=BC2-AB·AC=132-×5×12=139.
13.124 【解析】这批灯泡的平均使用寿命是=124(h).
14.1100 【解析】设直线的解析式为y=kx+b.∵直线过点(1,500),(2,700),∴,解得,∴y=200x+300,当x=4时,y=200×4+300=1100(元).
15.13 【解析】如图所示,延长CD交FG于H,∵矩形ABCD和矩形AEFG的一组邻边长分别为5和12,∴∠ADC=∠BCD=∠B=∠G=90°,AB=CD=GF=12,AD=BC=AG=5,AE∥GF,∴BG=AG+AB=17,∠DHG=∠ADC=90°,∴∠CHF=90°,四边形BCHG是矩形,∴CH=BG=17,GH=BC=5,∴HF=GF-GH=12-5=7,∴CF===13.
16.①②③④ 【解析】∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵点F,G分别是AD,BC的中点,∴AF=AD,BG=BC,∴AF=BG,∵AF∥BG,∴四边形ABGF是平行四边形,∴AB∥FG,∵CE⊥AB,∴CE⊥FG,故①正确;∵AD=2AB,AD=2AF,∴AB=AF,∴四边形ABGF是菱形,故②正确;∵CE⊥AB,∴∠BEC=90°,∵点G是BC的中点,∴BC=2EG,故③正确;如图,延长EF,交CD延长线于M,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF,∵F为AD中点,∴AF=FD,在△AEF和△DMF中,,∴△AEF≌△DMF(ASA),∴FE=MF,∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∴FC=EF=FM,同②可证得四边形CDFG是菱形,∴DF=DC,∴∠DCF=∠DFC,∴FG∥CD,∴∠DCF=∠CFG,∵FG⊥CE,∴∠EFG=∠CFG,∴∠EFG=∠DFC,故④正确.
三、解答题
17.解:(1)原式=3+-4=0; (3分)
(2)原式=[1+(-)][1-(-)]=1-(-)2=1-(2+3-2)=-4+2. (6分)
18.解:(1)证明:∵D,E为AB,AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,∴DE=CF. (3分)
(2)由(1)可知,DE∥BC,DE=CF,
∴四边形DCFE为平行四边形,∴EF=DC,
在等边△ABC中,D为AB中点,
∴CD⊥AB,∴CD==2,
∴EF=2. (6分)
19.解:(1)平均数:
=10(台);
众数:9台;中位数:9台.
(4分)
(2)不合理,因为达到指标的人数太少.应选9台比较合理,因为中位数和众数都是9台,能代表一般水平.
(6分)
20.解:(1)根据图象可知x=1; (2分)
(2)根据图象可知x<-0.5;
(4分)
(3)根据图象可知0(6分)
21.解:(1)240 348 (2分)
提示:由题意可得,当购买4千克种子时,需要付款60×4=240(元);
当购买6千克种子时,需要付款:60×5+(6-5)×60×0.8=348(元).
(2)由题意可得y=60×5+(x-5)×60×0.8=48x+60,
即y与x的函数关系式为y=48x+60(x>5). (5分)
(3)∵540>300,∴王伯伯一次性购买种子的质量超过5千克,
(6分)
令540=48x+60,解得x=10.
答:他购买种子的质量是10千克.
(8分)
22.解:(1)在Rt△CDG中,CD===10(米); (3分)
(2)∵CE⊥GB,AB⊥GB,∴∠BAC=∠EAC=45°,∴∠BCA=90°-45°=45°,∴BC=AB=60米,∴BG=BC+CG=120米, (4分)
如图,过D作DH⊥AB于点H,∵DG⊥GB,AB⊥GB,∴四边形BHDG是矩形,∴BH=DG=10米,DH=BG=120米,∴AH=AB-BH=50米,在Rt△ADH中,AD===130(米). (8分)
23.解:(1)证明:在矩形EFGH中,EH=FG,EH∥FG,
∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE,
在菱形ABCD中,AD∥BC,∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE. (4分)
(2)连接EG,在菱形ABCD中,AD∥BC,AD=BC,
∵E为AD中点,AE=ED,BG=DE,∴AE=BG,
∴四边形ABGE是平行四边形,∴AB=EG,
在矩形EFGH中,EG=FH=1,∴AB=1,
∴菱形周长为4. (10分)
24.解:(1)依据题意,设y1=k1x,y2=k2x+b.
∵y1=k1x过点(300,6000),
∴6000=k1×300,解得k1=20,
∴y1=20x,其对应的二元一次方程是y-20x=0; (2分)
∵y2=k2x+b经过点(0,3000)和点(300,6000),
∴,解得,
∴y2=10x+3000,其对应的二元一次方程是y-10x=3000,
∴二元一次方程组是.
(4分)
(2)由图可知方程组的解为,点(300,6000)的含义是当销售300件时,两种付费方式相同,都是6000元. (6分)
(3)第一种付费方案:没有底薪,每推销一件付20元推销费;第二种付费方案:底薪3000元,每推销一件付10元推销费; (8分)
(4)要根据自己的推销能力,如果估计每月能推销300件以上,就选第一种付费方案;如果认为自己每月推销不了300件,就选第二种付费方案.
(10分)
25.解:知识初探:证明:在正方形ABCD和正方形A1B1C1O中,∠OBE=∠OCF=45°,∠BOC=90°,OB=OC,∠EOF=90°,∴∠BOC-∠EOC=∠EOF-∠EOC,∴∠BOE=∠COF,
在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),∴OE=OF. (5分)
探究计算:在正方形ABCD中,∠ABC=90°,BC=AB=2,
在Rt△ABC中,AC===2,∴OC=OB=,
由知识初探可知△BOE≌△COF,
∴S△BOE=S△COF,
∴S四边形OECF=S△COF+S△OCE=S△BOE+S△OCE=S△BOC=××=1. (9分)
探究拓展:根据探究计算可知,四边形ABCD的面积是×4×4=8.
(12分)
时间:90分钟 满分:120分 考试范围:下册全部内容
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共30分)
1.下列二次根式中,是最简二次根式的是 ( )
A. B. C. D.
2.为筹备班级的初中毕业联欢会,班委会经过讨论决定在苹果、橘子、香蕉、梨四种水果中选出一种购买,班长对全班学生爱吃哪种水果做了调查,则最终在决定购买哪种水果时,下面的调查数据中最值得关注的是 ( )
A.众数 B.平均数 C.中位数 D.方差
3.如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是 ( )
A.16 B.20 C.30 D.60
4.如图,数轴上点A对应的数是-1,点C对应的数是-3,BC⊥AC,垂足为点C,且BC=1,以点A为圆心,AB的长为半径画弧,交数轴于点D,则点D表示的数为( )
A.-1 B. C.-1 D.
5.若点P(-2,4)关于y轴的对称点在一次函数y=x+b的图象上,则b的值为( )
A.-3 B.3 C.-2 D.2
6.数据8,7,6,7,6,5,4,5,8,6的中位数是 ( )
A.8 B.7 C.6 D.5
7.如图,函数y1=-2x和y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是 ( )
A.x>2 B.x<2 C.x>-1 D.x<-1
8.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,若∠BAD=70°,则∠CFD的度数为 ( )
A.50° B.60° C.70° D.80°
9.在某一阶段,某商品的销售量与销售价之间存在如表关系:
销售价/元 90 100 110 120 130 140
销售量/件 90 80 70 60 50 40
设该商品的销售价为x元,销售量为y件,估计:当x=127时,y的值为 ( )
A.63 B.59 C.53 D.43
10.如图,在△ABC中,AB=6,BC=8,∠B=90°,若P是AC上的一个动点,则AP+BP+CP的最小值是 ( )
A.14.8 B.15 C.15.2 D.16
二、填空题(每小题3分,共18分)
11.矩形相邻两边长分别为,,则它的周长是 .
12.如图,以Rt△ABC的两条直角边和斜边为边长分别作正方形,其中正方形ABFG,正方形ACDE的面积分别为25,144,则阴影部分的面积为 .
13.某灯泡厂为测量一批灯泡的使用寿命,从中抽查了100只灯泡,它们的使用寿命如下表所示:
使用寿命x/h 60≤x<100 100≤x<140 140≤x<180
灯泡只数 30 30 40
则这批灯泡的平均使用寿命是 h.
14.如果某公司一销售人员的个人月收入y与其每月的销售量x成一次函数(如图所示),那么此销售人员的销售量在4千件时的月收入是 元.
15.如图,将一组邻边长分别为5和12的两个矩形ABCD和矩形AEFG拼成“L”形图案,则线段CF的长为 .
16.如图,在平行四边形ABCD中,AD=2AB,CE⊥AB于点E,点F,G分别是AD,BC的中点,连接CF,EF,FG,EG,下列四种说法:①CE⊥FG;②四边形ABGF是菱形;③BC=2EG;④∠DFC=∠EFG.其中正确的是 .(填序号)
三、解答题(本大题共9小题,共72分)
17.(6分)计算:(1)+-;(2)(1+-)(1-+).
18.(6分)如图,等边△ABC的边长是4,D,E 分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD,EF.
(1)求证:DE=CF.
(2)求EF的长.
19.(6分)某销售公司有营销人员14人,销售部为了制定某种品牌的净水器的月销售量定额,统计了这14人在某月的销售量如下表:
销售台数 20 18 14 9 7 4
人数 1 1 2 5 3 2
(1)这14位销售员该月销售量的平均数、众数和中位数各是多少台
(2)销售部经理把每位销售员每月销售量定为10台,你认为是否合理,为什么 如果不合理,请你设计一个比较合理的销售定额,并说明理由.
20.(6分)函数y=kx+b的图象如图所示,利用函数图象解答下列问题:
(1)解方程kx+b=1.5;
(2)解不等式kx+b<0;
(3)解不等式组0.5
(1)根据题意,补充下表:
购买种子的质量/千克 3 4 5 6 …
付款金额/元 180 300 …
(2)设购买种子的质量为x(x>5)千克,付款金额为y元,求y与x的函数关系式;
(3)若王伯伯一次性购买该种子花了540元,求他购买种子的质量.
22.(8分)“儿童散学归来早,忙趁东风放纸鸢.”如图,小明站在C处,同时小亮在斜坡的D处,DG⊥GB且DG=10米,CG=60米,CE⊥GB.(不考虑两人身高,点G,C,B在同一水平线上)
(1)求小明与小亮之间的距离CD.(结果保留根号)
(2)若风筝A在小明的北偏东45°方向上,且高度AB为60米,AB⊥GB,求此时风筝A到小亮的距离AD.
23.(10分)如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD中点,FH=1,求菱形ABCD的周长.
24.(10分)某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费.如图所示,图中表示了公司每月付给推销员推销费的两种方案,根据图中所示信息解答下列问题:
(1)写出y1与y2对应的二元一次方程组;(不考虑取值范围)
(2)请直接写出(1)中方程组的解,并解释(300,6000)的含义;
(3)解释图中表示的两种方案是如何付推销费的;
(4)如果你是推销员,应如何选择付费方案
25.(12分)综合与实践:如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等,OA1交BC于点E,OC1交CD于点F.
知识初探:求证:OE=OF.
探究计算:若AB=2,求四边形OECF的面积.
探究拓展:如图2,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC,若AC=4,求四边形ABCD的面积.
图1 图2
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D A B A B C D C C A
2.A 【解析】爱吃的水果人数越多,班长就应多买,而众数反映的就是.
3.B 【解析】∵DE平分∠ADC,∴∠ADE=∠CDE,在 ABCD中,∴AD∥BC,∴∠ADE=∠CED,∴∠CDE=∠CED,∴CE=CD,在 ABCD中,AD=6,BE=2,∴AD=BC=6,∴CE=BC-BE=6-2=4,∴CD=AB=4,∴ ABCD的周长=6+6+4+4=20.
4.A 【解析】∵BC⊥AC,∴∠BCA=90°,∴AB===,∵以A为圆心,AB为半径画弧,交数轴于点D,∴AD=AB=,∴点D表示的数是-1.
5.B 【解析】∵点P(-2,4)关于y轴的对称点为(2,4),∴把(2,4)代入一次函数y=x+b,得2×+b=4,解得b=3.
6.C 【解析】把这组数据从小到大排序为4,5,5,6,6,6,7,7,8,8,所以中位数是=6.
7.D 【解析】∵函数y1=-2x的图象经过点A(m,2),∴-2m=2,解得m=-1,∴A(-1,2),观察两个函数图象可知,当函数y1=-2x在函数y2=ax+3的图象上方时,x<-1,即不等式-2x>ax+3的解集为x<-1.
8.C 【解析】如图所示,连接BF,∵四边形ABCD是菱形,∴∠BAC=∠BAD=×70°=35°,∠BCF=∠DCF=∠BAC,BC=DC,∠ABC=180°-∠BAD=180°-70°=110°,∵EF是线段AB的垂直平分线,∴AF=BF,∴∠DCF=∠ABF=∠BAC=35°,∴∠CBF=∠ABC-∠ABF=110°-35°=75°,在△BCF和△DCF中,,∴△BCF≌△DCF,∴∠CDF=∠CBF=75°,∴∠CFD=180°-∠CDF-∠DCF=180°-75°-35°=70°.
9.C 【解析】由图表可以看出y与x符合一次函数关系,设y=kx+b(k≠0),把x=90,y=90和x=100,y=80代入得,解得,则y=-x+180,当x=127时,y=-127+180=53.
10.A 【解析】∵∠B=90°,AB=6,BC=8,∴AC===10,∵AP+BP+PC=BP+AC=BP+10,根据垂线段最短可知,当BP⊥AC时,BP的值最小,最小值BP===4.8,∴AP+BP+CP的最小值=10+4.8=14.8.
二、填空题
11 12 13 14 15 16
6 139 124 1100 13 ①②③④
11.6 【解析】矩形的周长是2×(+)=2×(+2)=6.
12.139 【解析】根据题意知AB2=25,AC2=144,∴AB=5,AC=12,BC===13,∴S阴影=BC2-AB·AC=132-×5×12=139.
13.124 【解析】这批灯泡的平均使用寿命是=124(h).
14.1100 【解析】设直线的解析式为y=kx+b.∵直线过点(1,500),(2,700),∴,解得,∴y=200x+300,当x=4时,y=200×4+300=1100(元).
15.13 【解析】如图所示,延长CD交FG于H,∵矩形ABCD和矩形AEFG的一组邻边长分别为5和12,∴∠ADC=∠BCD=∠B=∠G=90°,AB=CD=GF=12,AD=BC=AG=5,AE∥GF,∴BG=AG+AB=17,∠DHG=∠ADC=90°,∴∠CHF=90°,四边形BCHG是矩形,∴CH=BG=17,GH=BC=5,∴HF=GF-GH=12-5=7,∴CF===13.
16.①②③④ 【解析】∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵点F,G分别是AD,BC的中点,∴AF=AD,BG=BC,∴AF=BG,∵AF∥BG,∴四边形ABGF是平行四边形,∴AB∥FG,∵CE⊥AB,∴CE⊥FG,故①正确;∵AD=2AB,AD=2AF,∴AB=AF,∴四边形ABGF是菱形,故②正确;∵CE⊥AB,∴∠BEC=90°,∵点G是BC的中点,∴BC=2EG,故③正确;如图,延长EF,交CD延长线于M,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF,∵F为AD中点,∴AF=FD,在△AEF和△DMF中,,∴△AEF≌△DMF(ASA),∴FE=MF,∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∴FC=EF=FM,同②可证得四边形CDFG是菱形,∴DF=DC,∴∠DCF=∠DFC,∴FG∥CD,∴∠DCF=∠CFG,∵FG⊥CE,∴∠EFG=∠CFG,∴∠EFG=∠DFC,故④正确.
三、解答题
17.解:(1)原式=3+-4=0; (3分)
(2)原式=[1+(-)][1-(-)]=1-(-)2=1-(2+3-2)=-4+2. (6分)
18.解:(1)证明:∵D,E为AB,AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,∴DE=CF. (3分)
(2)由(1)可知,DE∥BC,DE=CF,
∴四边形DCFE为平行四边形,∴EF=DC,
在等边△ABC中,D为AB中点,
∴CD⊥AB,∴CD==2,
∴EF=2. (6分)
19.解:(1)平均数:
=10(台);
众数:9台;中位数:9台.
(4分)
(2)不合理,因为达到指标的人数太少.应选9台比较合理,因为中位数和众数都是9台,能代表一般水平.
(6分)
20.解:(1)根据图象可知x=1; (2分)
(2)根据图象可知x<-0.5;
(4分)
(3)根据图象可知0
21.解:(1)240 348 (2分)
提示:由题意可得,当购买4千克种子时,需要付款60×4=240(元);
当购买6千克种子时,需要付款:60×5+(6-5)×60×0.8=348(元).
(2)由题意可得y=60×5+(x-5)×60×0.8=48x+60,
即y与x的函数关系式为y=48x+60(x>5). (5分)
(3)∵540>300,∴王伯伯一次性购买种子的质量超过5千克,
(6分)
令540=48x+60,解得x=10.
答:他购买种子的质量是10千克.
(8分)
22.解:(1)在Rt△CDG中,CD===10(米); (3分)
(2)∵CE⊥GB,AB⊥GB,∴∠BAC=∠EAC=45°,∴∠BCA=90°-45°=45°,∴BC=AB=60米,∴BG=BC+CG=120米, (4分)
如图,过D作DH⊥AB于点H,∵DG⊥GB,AB⊥GB,∴四边形BHDG是矩形,∴BH=DG=10米,DH=BG=120米,∴AH=AB-BH=50米,在Rt△ADH中,AD===130(米). (8分)
23.解:(1)证明:在矩形EFGH中,EH=FG,EH∥FG,
∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE,
在菱形ABCD中,AD∥BC,∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE. (4分)
(2)连接EG,在菱形ABCD中,AD∥BC,AD=BC,
∵E为AD中点,AE=ED,BG=DE,∴AE=BG,
∴四边形ABGE是平行四边形,∴AB=EG,
在矩形EFGH中,EG=FH=1,∴AB=1,
∴菱形周长为4. (10分)
24.解:(1)依据题意,设y1=k1x,y2=k2x+b.
∵y1=k1x过点(300,6000),
∴6000=k1×300,解得k1=20,
∴y1=20x,其对应的二元一次方程是y-20x=0; (2分)
∵y2=k2x+b经过点(0,3000)和点(300,6000),
∴,解得,
∴y2=10x+3000,其对应的二元一次方程是y-10x=3000,
∴二元一次方程组是.
(4分)
(2)由图可知方程组的解为,点(300,6000)的含义是当销售300件时,两种付费方式相同,都是6000元. (6分)
(3)第一种付费方案:没有底薪,每推销一件付20元推销费;第二种付费方案:底薪3000元,每推销一件付10元推销费; (8分)
(4)要根据自己的推销能力,如果估计每月能推销300件以上,就选第一种付费方案;如果认为自己每月推销不了300件,就选第二种付费方案.
(10分)
25.解:知识初探:证明:在正方形ABCD和正方形A1B1C1O中,∠OBE=∠OCF=45°,∠BOC=90°,OB=OC,∠EOF=90°,∴∠BOC-∠EOC=∠EOF-∠EOC,∴∠BOE=∠COF,
在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),∴OE=OF. (5分)
探究计算:在正方形ABCD中,∠ABC=90°,BC=AB=2,
在Rt△ABC中,AC===2,∴OC=OB=,
由知识初探可知△BOE≌△COF,
∴S△BOE=S△COF,
∴S四边形OECF=S△COF+S△OCE=S△BOE+S△OCE=S△BOC=××=1. (9分)
探究拓展:根据探究计算可知,四边形ABCD的面积是×4×4=8.
(12分)
同课章节目录
