期中闯关测试卷(第十六章~第十八章)(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 期中闯关测试卷(第十六章~第十八章)(含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 260.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:24:07 | ||
图片预览


文档简介
期中测试卷
时间:90分钟 满分:120分 考试范围:第十六章~第十八章
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共30分)
1.下列二次根式中,是最简二次根式的是 ( )
A. B. C. D.
2.如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形是直角三角形的是 ( )
A.△ABD B.△ADC C.△BCD D.△ABC
3.如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为 ( )
A.2 B.2 C.3 D.
4.估计×+÷的运算结果应在 ( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
5.已知a=3+,b=3-,则代数式的值是 ( )
A.24 B.±2 C.2 D.2
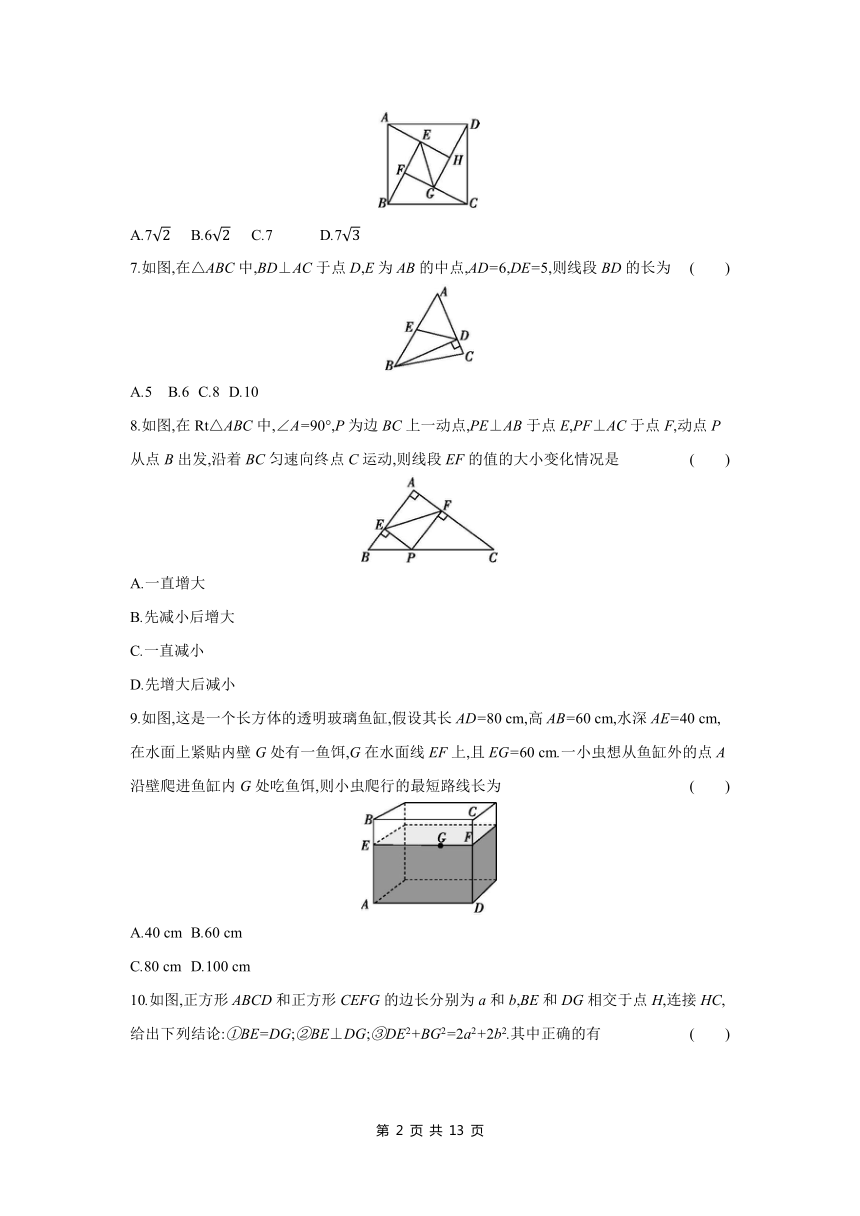
6.如图,△ABE,△BCF,△CDG,△DAH是四个全等的直角三角形,其中AE=5,AB=13,则EG的长为 ( )
A.7 B.6 C.7 D.7
7.如图,在△ABC中,BD⊥AC于点D,E为AB的中点,AD=6,DE=5,则线段BD的长为 ( )
A.5 B.6 C.8 D.10
8.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值的大小变化情况是 ( )
A.一直增大
B.先减小后增大
C.一直减小
D.先增大后减小
9.如图,这是一个长方体的透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A沿壁爬进鱼缸内G处吃鱼饵,则小虫爬行的最短路线长为 ( )
A.40 cm B.60 cm
C.80 cm D.100 cm
10.如图,正方形ABCD和正方形CEFG的边长分别为a和b,BE和DG相交于点H,连接HC,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题3分,共18分)
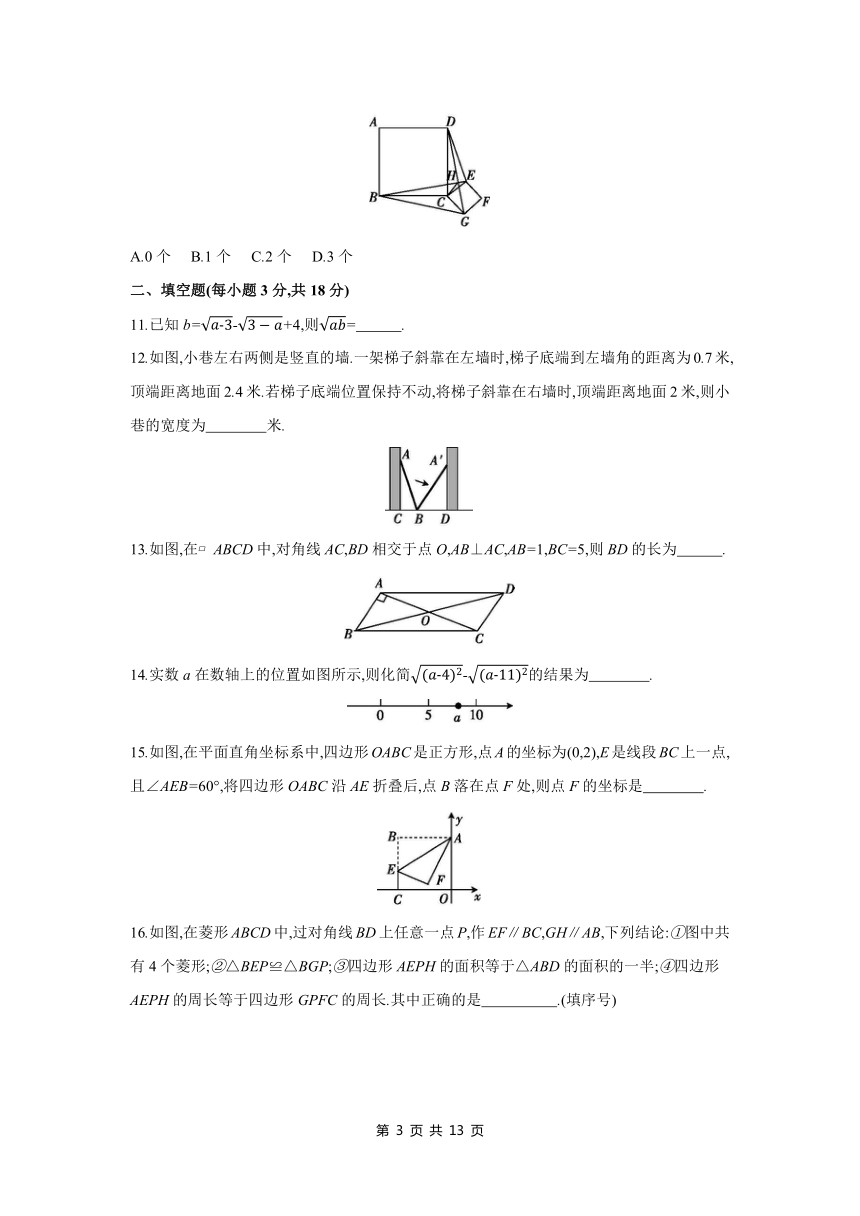
11.已知b=-+4,则= .
12.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为 米.
13.如图,在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则BD的长为 .
14.实数a在数轴上的位置如图所示,则化简-的结果为 .
15.如图,在平面直角坐标系中,四边形OABC是正方形,点A的坐标为(0,2),E是线段BC上一点,且∠AEB=60°,将四边形OABC沿AE折叠后,点B落在点F处,则点F的坐标是 .
16.如图,在菱形ABCD中,过对角线BD上任意一点P,作EF∥BC,GH∥AB,下列结论:①图中共有4个菱形;②△BEP≌△BGP;③四边形AEPH的面积等于△ABD的面积的一半;④四边形AEPH的周长等于四边形GPFC的周长.其中正确的是 .(填序号)
三、解答题(本大题共9小题,共72分)
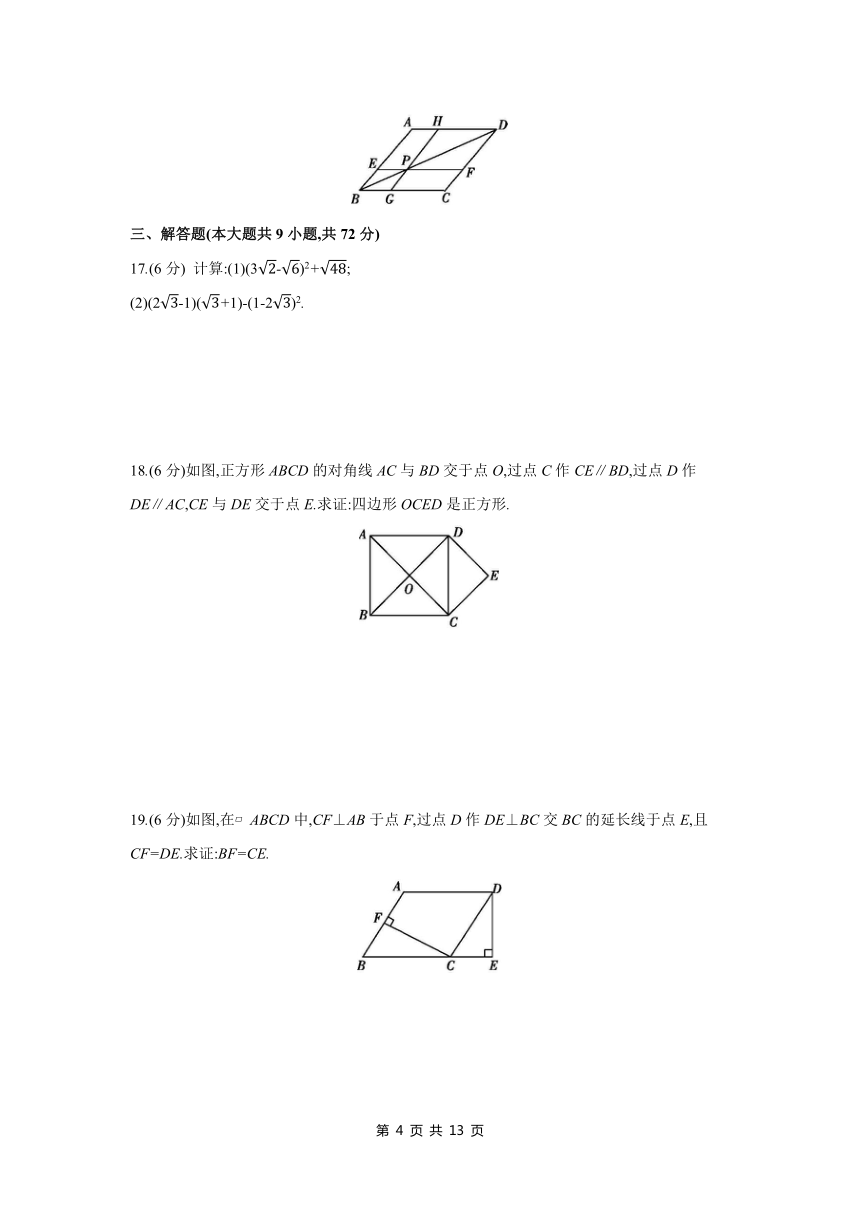
17.(6分) 计算:(1)(3-)2+;
(2)(2-1)(+1)-(1-2)2.
18.(6分)如图,正方形ABCD的对角线AC与BD交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE交于点E.求证:四边形OCED是正方形.
19.(6分)如图,在 ABCD中,CF⊥AB于点F,过点D作DE⊥BC交BC的延长线于点E,且CF=DE.求证:BF=CE.
20.(6分)如图,小方格都是边长为1的正方形.
(1)求AD和CD的长;
(2)求证:∠ABC=90°.
21.(8分)已知长方形的长为,宽为.
(1)求长方形的周长.
(2)求与长方形面积相等的正方形的周长,并比较正方形周长与长方形周长的大小.
(3)通过计算,你从中得到了什么启示
22.(8分)如图1,正方形ABCD的边长为4,点E在边BC上,且BE=BC,F为边CD的中点,连接AF,AE,EF.
(1)判断△AEF的形状,并说明理由;
(2)如图2,设AE的中点为O,判断∠BOF和∠BAF之间存在怎样的数量关系,并证明你的结论.
23.(10分)如图,在 ABCD中,AC=12 cm,BD=16 cm,在对角线BD上,E,F两点分别从点B,D出发往终点D,B运动,它们的速度都是每秒1 cm,且同时出发,同时停止,若它们的运动时间为t秒.
(1)当t≠8时,判断四边形AECF的形状,并说明理由.
(2)当运动时间t为多少时,四边形AECF为矩形
24.(10分)如图①,在菱形ABCD中,E,F分别是边CB,DC上的点,∠B=∠EAF=60°.
(1)求证:∠BAE=∠CEF.
(2)如图②,若点E,F分别移动到边CB,DC的延长线上,其余条件不变,请猜想∠BAE与∠CEF的大小关系,并给予证明.
25.(12分)(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,线段GF与GC有何数量关系 并证明你的结论.
(2)类比探究:如图2,将(1)中的矩形ABCD改为平行四边形ABCD,其他条件不变,(1)中的结论是否仍然成立 请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D A B C C A C B D D
1.D 【解析】=,不是最简二次根式;=2,不是最简二次根式;=2,不是最简二次根式;是最简二次根式.
2.A 【解析】∵AB2=5,BD2=5,CD2=5,AC2=13,AD2=10,BC2=16,∴AB2+BD2=AD2,AD2+DC2≠AC2,BD2+DC2≠BC2,AB2+AC2≠BC2,∴△ABD是直角三角形.
3.B 【解析】∵四边形ABCD是菱形,∴AC⊥BD,BD=2BO,∵∠ABC=60°,∴∠ABO=30°,∵AB=2,∴AO=1,∴BO=,∴BD=2.
4.C 【解析】原式=2×+÷=2+,∵2<<3,∴4<2+<5.
5.C 【解析】∵a=3+,b=3-,∴a+b=6,ab=4,∴===2.
6.A 【解析】由勾股定理得BE===12,∵△ABE,△BCF,△CDG,△DAH是四个全等的直角三角形,∴∠AEB=∠BFC=∠CGD=90°,BF=CG=DH=AE=5,∴∠FEH=∠EFC=∠FGD=90°,EF=EH=12-5=7,∴四边形EFGH为正方形,∴EG==7.
7.C 【解析】∵BD⊥AC于点D,点E为AB的中点,∴在Rt△ABD中,AB=2DE=2×5=10,BD==8.
8.B 【解析】如图,连接AP,∵∠A=90°,PE⊥AB,PF⊥AC,∴四边形AFPE是矩形,∴EF=AP,由垂线段最短可得AP⊥BC时,AP最短,则线段EF的值最小,∴动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值的大小变化情况是先减小后增大.
9.D 【解析】如图所示,作点A关于BC的对称点A',连接A'G交BC于点Q,小虫沿着A→Q→G的路线爬行时路程最短.在Rt△A'EG中,A'E=80 cm,EG=60 cm,∴AQ+QG=A'Q+QG=A'G==100 cm.
10.D 【解析】如图,∵四边形ABCD和EFGC都为正方形,∴BC=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCD+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,在△BCE和△DCG中,∵∴△BCE≌△DCG,∴BE=DG,∴∠1=∠2,∵∠1+∠4=∠3+∠1=90°,∴∠2+∠3=90°,∴∠BHD=90°,∴BE⊥DG,故①②正确;连接BD,EG,∴DH2+BH2=BD2=BC2+CD2=2a2,EH2+HG2=EG2=CG2+CE2=2b2,则BG2+DE2=DH2+BH2+EH2+HG2=2a2+2b2,故③正确.
二、填空题
11 12 13 14
2 2.2 2 2a-15
15 16
(-1,2-) ②④
11.2 【解析】由题意得,解得a=3,∴b=4,∴===2.
12.2.2 【解析】在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,∴AB2=0.72+2.42=6.25.在Rt△A'BD中,∵∠A'DB=90°,A'D=2米,BD2+A'D2=A'B2,∴BD2+22=6.25,∴BD2=2.25,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2(米).
13.2 【解析】∵四边形ABCD是平行四边形,∴OA=OC=AC,OB=OD=BD,∵AB⊥AC,∴∠BAC=90°,∴AC===2,∴OA=AC=,∴OB===,∴BD=2OB=2.
14.2a-15 【解析】由图可知515.(-1,2-) 【解析】∵∠AEB=60°,四边形OABC沿AE折叠后,点B落在点F,∴∠BAE=∠EAF=∠FAO=30°,AF=AB=2.如图,作FD⊥CO于点D,FG⊥AO于点G,∠FAG=30°,∴FG=1,AG=,∴GO=2-,∴点F的坐标为(-1,2-).
16.②④ 【解析】由题意可知图中有3个菱形,菱形ABCD、菱形HPFD、菱形BEPG,∴①错误;∵四边形BEPG,∴PE=BG=PG=BE,在△BEP和△BGP中,∴△BEP≌△BGP(SSS),∴②正确;∵只有当H为AD中点,E为AB中点时,四边形AEPH的面积等于△ABD的面积的一半,∴③错误;易证四边形HPFD、四边形BEPG是菱形,四边形AEPH、四边形PFCG是平行四边形,∴BE=PE,∴AH=PE=BG=BE=CF=PG,同理AE=HP=DF=PF=CG,∴四边形AEPH的周长=四边形GPFC的周长,∴④正确.
三、解答题
17.解:(1)原式=18-6+6+4=18-12+6+4=24-8; (3分)
(2)原式=6+2--1-13+4=-8+5. (6分)
18.证明:∵CE∥BD,DE∥AC,∴四边形OCED是平行四边形, (2分)
∵正方形ABCD的对角线AC与BD交于点O,
∴OD=OC,∠DOC=90°,
∴四边形OCED是正方形. (6分)
19.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠B=∠DCE.
又∵CF⊥AB,DE⊥BC,
∴∠BFC=∠E=90°. (3分)
在△BCF和△CDE中,
∴△BCF≌△CDE(AAS),
∴BF=CE. (6分)
20.解:(1)由图可知AD==,CD==5. (3分)
(2)证明:如图,连接AC,由图可知AB2=22+32=13,BC2=22+32=13,AC2=12+52=26,
∴AB2+BC2=13+13=26=AC2,
∴△ABC是以AC为斜边的直角三角形,
∴∠ABC=90°. (6分)
21.解:(1)长方形的周长为2×(+)=2×(2+)=6. (3分)
(2)∵×=2×=4,∴正方形的边长为=2,∴正方形的周长为2×4=8,
而6>8,∴长方形的周长大于正方形的周长. (6分)
(3)通过计算可得当长方形的面积与正方形的面积相同时,长方形的周长大于正方形的周长. (8分)
22.解:(1)△AEF是直角三角形. (1分)
理由:∵四边形ABCD是正方形,∴AB=BC=CD=DA=4,
∵BE=BC,∴EC=1,BE=3,
∵F为CD的中点,∴DF=FC=2,
∴EF2=12+22=5,AF2=42+22=20,AE2=42+32=25,∴AE2=EF2+AF2,
∴△AEF是直角三角形. (4分)
(2)∠BOF=2∠BAF. (5分)
证明: ∵AE的中点为O,△ABE,△AEF是直角三角形,
∴AO=BO=OE,OE=OA=OF,∴∠BAO=∠OBA,∠OAF=∠OFA,
∴∠BOF=∠BAO+∠OBA+∠OAF+∠OFA=2∠BAF. (8分)
23.解:(1)四边形AECF是平行四边形. (1分)
理由:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵BE=DF=t,∴EO=FO.
又∵AO=CO,
∴四边形AECF是平行四边形. (5分)
(2)若四边形AECF是矩形,则AC=EF.
当E在BO上时,12=16-2t,解得t=2;
当E有OD上时,12=2t-16,解得t=14.
∴当t=2或14时,四边形AECF为矩形. (10分)
24.解:(1)证明:如图①,连接AC. (1分)
∵四边形ABCD是菱形,∴AB=BC,AB∥CD,CA平分∠BCD.
∵∠B=60°,∴△ABC是等边三角形,
∴∠B=∠BAC=60°,AB=AC.
∵AB∥CD,∴∠ACD=∠BAC=60°,
∴∠B=∠ACD=60°.
∵∠EAF=60°,∴∠BAE+∠EAC=∠EAC+∠CAF=60°,∴∠BAE=∠CAF.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),∴AE=AF,
∴△AEF为等边三角形,∴∠AEF=60°,
∴∠CEF+∠AEB=120°,
∵∠BAE+∠AEB=120°,
∴∠BAE=∠CEF. (6分)
(2)∠BAE=∠CEF. (7分)
证明:如图②,连接AC,由(1)知∠ABC=∠ACD=60°,∠EAF=∠BAC=60°,AB=AC,
∴∠ABE=∠ACF=120°,∠BAE=∠CAF.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),∴AE=AF,
∴△AEF为等边三角形,∴∠AEF=60°,∴∠AEB+∠CEF=60°,
∵∠AEB+∠BAE=∠ABC=60°,
∴∠BAE=∠CEF. (10分)
25.解:(1)GF=GC. (1分)
证明:如图1,连接EG,∵E是BC的中点,∴BE=CE,
∵将△ABE沿AE折叠后得到△AFE,∴BE=EF,∴EF=EC,
∵EG=EG,∠C=∠EFG=90°,∴Rt△ECG≌Rt△EFG(HL),∴FG=CG. (5分)
(2)(1)中的结论仍然成立. (6分)
理由:如图2,连接FC.
∵E是BC的中点,∴BE=CE.
将△ABE沿AE折叠后得到△AFE,∴BE=EF,∠B=∠AFE,∴EF=EC,∴∠EFC=∠ECF.
∵平行四边形ABCD,∴AB∥CD,
∴∠ECD=180°-∠B,∠EFG=180°-∠AFE=180°-∠B,∴∠ECD=∠EFG.
∵∠GFC=∠GFE-∠EFC,∠GCF=∠ECG-∠ECF,∴∠GFC=∠GCF,
∴FG=GC. (12分)
时间:90分钟 满分:120分 考试范围:第十六章~第十八章
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共30分)
1.下列二次根式中,是最简二次根式的是 ( )
A. B. C. D.
2.如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形是直角三角形的是 ( )
A.△ABD B.△ADC C.△BCD D.△ABC
3.如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为 ( )
A.2 B.2 C.3 D.
4.估计×+÷的运算结果应在 ( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
5.已知a=3+,b=3-,则代数式的值是 ( )
A.24 B.±2 C.2 D.2
6.如图,△ABE,△BCF,△CDG,△DAH是四个全等的直角三角形,其中AE=5,AB=13,则EG的长为 ( )
A.7 B.6 C.7 D.7
7.如图,在△ABC中,BD⊥AC于点D,E为AB的中点,AD=6,DE=5,则线段BD的长为 ( )
A.5 B.6 C.8 D.10
8.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值的大小变化情况是 ( )
A.一直增大
B.先减小后增大
C.一直减小
D.先增大后减小
9.如图,这是一个长方体的透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A沿壁爬进鱼缸内G处吃鱼饵,则小虫爬行的最短路线长为 ( )
A.40 cm B.60 cm
C.80 cm D.100 cm
10.如图,正方形ABCD和正方形CEFG的边长分别为a和b,BE和DG相交于点H,连接HC,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题3分,共18分)
11.已知b=-+4,则= .
12.如图,小巷左右两侧是竖直的墙.一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为 米.
13.如图,在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则BD的长为 .
14.实数a在数轴上的位置如图所示,则化简-的结果为 .
15.如图,在平面直角坐标系中,四边形OABC是正方形,点A的坐标为(0,2),E是线段BC上一点,且∠AEB=60°,将四边形OABC沿AE折叠后,点B落在点F处,则点F的坐标是 .
16.如图,在菱形ABCD中,过对角线BD上任意一点P,作EF∥BC,GH∥AB,下列结论:①图中共有4个菱形;②△BEP≌△BGP;③四边形AEPH的面积等于△ABD的面积的一半;④四边形AEPH的周长等于四边形GPFC的周长.其中正确的是 .(填序号)
三、解答题(本大题共9小题,共72分)
17.(6分) 计算:(1)(3-)2+;
(2)(2-1)(+1)-(1-2)2.
18.(6分)如图,正方形ABCD的对角线AC与BD交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE交于点E.求证:四边形OCED是正方形.
19.(6分)如图,在 ABCD中,CF⊥AB于点F,过点D作DE⊥BC交BC的延长线于点E,且CF=DE.求证:BF=CE.
20.(6分)如图,小方格都是边长为1的正方形.
(1)求AD和CD的长;
(2)求证:∠ABC=90°.
21.(8分)已知长方形的长为,宽为.
(1)求长方形的周长.
(2)求与长方形面积相等的正方形的周长,并比较正方形周长与长方形周长的大小.
(3)通过计算,你从中得到了什么启示
22.(8分)如图1,正方形ABCD的边长为4,点E在边BC上,且BE=BC,F为边CD的中点,连接AF,AE,EF.
(1)判断△AEF的形状,并说明理由;
(2)如图2,设AE的中点为O,判断∠BOF和∠BAF之间存在怎样的数量关系,并证明你的结论.
23.(10分)如图,在 ABCD中,AC=12 cm,BD=16 cm,在对角线BD上,E,F两点分别从点B,D出发往终点D,B运动,它们的速度都是每秒1 cm,且同时出发,同时停止,若它们的运动时间为t秒.
(1)当t≠8时,判断四边形AECF的形状,并说明理由.
(2)当运动时间t为多少时,四边形AECF为矩形
24.(10分)如图①,在菱形ABCD中,E,F分别是边CB,DC上的点,∠B=∠EAF=60°.
(1)求证:∠BAE=∠CEF.
(2)如图②,若点E,F分别移动到边CB,DC的延长线上,其余条件不变,请猜想∠BAE与∠CEF的大小关系,并给予证明.
25.(12分)(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,线段GF与GC有何数量关系 并证明你的结论.
(2)类比探究:如图2,将(1)中的矩形ABCD改为平行四边形ABCD,其他条件不变,(1)中的结论是否仍然成立 请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D A B C C A C B D D
1.D 【解析】=,不是最简二次根式;=2,不是最简二次根式;=2,不是最简二次根式;是最简二次根式.
2.A 【解析】∵AB2=5,BD2=5,CD2=5,AC2=13,AD2=10,BC2=16,∴AB2+BD2=AD2,AD2+DC2≠AC2,BD2+DC2≠BC2,AB2+AC2≠BC2,∴△ABD是直角三角形.
3.B 【解析】∵四边形ABCD是菱形,∴AC⊥BD,BD=2BO,∵∠ABC=60°,∴∠ABO=30°,∵AB=2,∴AO=1,∴BO=,∴BD=2.
4.C 【解析】原式=2×+÷=2+,∵2<<3,∴4<2+<5.
5.C 【解析】∵a=3+,b=3-,∴a+b=6,ab=4,∴===2.
6.A 【解析】由勾股定理得BE===12,∵△ABE,△BCF,△CDG,△DAH是四个全等的直角三角形,∴∠AEB=∠BFC=∠CGD=90°,BF=CG=DH=AE=5,∴∠FEH=∠EFC=∠FGD=90°,EF=EH=12-5=7,∴四边形EFGH为正方形,∴EG==7.
7.C 【解析】∵BD⊥AC于点D,点E为AB的中点,∴在Rt△ABD中,AB=2DE=2×5=10,BD==8.
8.B 【解析】如图,连接AP,∵∠A=90°,PE⊥AB,PF⊥AC,∴四边形AFPE是矩形,∴EF=AP,由垂线段最短可得AP⊥BC时,AP最短,则线段EF的值最小,∴动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值的大小变化情况是先减小后增大.
9.D 【解析】如图所示,作点A关于BC的对称点A',连接A'G交BC于点Q,小虫沿着A→Q→G的路线爬行时路程最短.在Rt△A'EG中,A'E=80 cm,EG=60 cm,∴AQ+QG=A'Q+QG=A'G==100 cm.
10.D 【解析】如图,∵四边形ABCD和EFGC都为正方形,∴BC=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCD+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,在△BCE和△DCG中,∵∴△BCE≌△DCG,∴BE=DG,∴∠1=∠2,∵∠1+∠4=∠3+∠1=90°,∴∠2+∠3=90°,∴∠BHD=90°,∴BE⊥DG,故①②正确;连接BD,EG,∴DH2+BH2=BD2=BC2+CD2=2a2,EH2+HG2=EG2=CG2+CE2=2b2,则BG2+DE2=DH2+BH2+EH2+HG2=2a2+2b2,故③正确.
二、填空题
11 12 13 14
2 2.2 2 2a-15
15 16
(-1,2-) ②④
11.2 【解析】由题意得,解得a=3,∴b=4,∴===2.
12.2.2 【解析】在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,∴AB2=0.72+2.42=6.25.在Rt△A'BD中,∵∠A'DB=90°,A'D=2米,BD2+A'D2=A'B2,∴BD2+22=6.25,∴BD2=2.25,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2(米).
13.2 【解析】∵四边形ABCD是平行四边形,∴OA=OC=AC,OB=OD=BD,∵AB⊥AC,∴∠BAC=90°,∴AC===2,∴OA=AC=,∴OB===,∴BD=2OB=2.
14.2a-15 【解析】由图可知5
16.②④ 【解析】由题意可知图中有3个菱形,菱形ABCD、菱形HPFD、菱形BEPG,∴①错误;∵四边形BEPG,∴PE=BG=PG=BE,在△BEP和△BGP中,∴△BEP≌△BGP(SSS),∴②正确;∵只有当H为AD中点,E为AB中点时,四边形AEPH的面积等于△ABD的面积的一半,∴③错误;易证四边形HPFD、四边形BEPG是菱形,四边形AEPH、四边形PFCG是平行四边形,∴BE=PE,∴AH=PE=BG=BE=CF=PG,同理AE=HP=DF=PF=CG,∴四边形AEPH的周长=四边形GPFC的周长,∴④正确.
三、解答题
17.解:(1)原式=18-6+6+4=18-12+6+4=24-8; (3分)
(2)原式=6+2--1-13+4=-8+5. (6分)
18.证明:∵CE∥BD,DE∥AC,∴四边形OCED是平行四边形, (2分)
∵正方形ABCD的对角线AC与BD交于点O,
∴OD=OC,∠DOC=90°,
∴四边形OCED是正方形. (6分)
19.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠B=∠DCE.
又∵CF⊥AB,DE⊥BC,
∴∠BFC=∠E=90°. (3分)
在△BCF和△CDE中,
∴△BCF≌△CDE(AAS),
∴BF=CE. (6分)
20.解:(1)由图可知AD==,CD==5. (3分)
(2)证明:如图,连接AC,由图可知AB2=22+32=13,BC2=22+32=13,AC2=12+52=26,
∴AB2+BC2=13+13=26=AC2,
∴△ABC是以AC为斜边的直角三角形,
∴∠ABC=90°. (6分)
21.解:(1)长方形的周长为2×(+)=2×(2+)=6. (3分)
(2)∵×=2×=4,∴正方形的边长为=2,∴正方形的周长为2×4=8,
而6>8,∴长方形的周长大于正方形的周长. (6分)
(3)通过计算可得当长方形的面积与正方形的面积相同时,长方形的周长大于正方形的周长. (8分)
22.解:(1)△AEF是直角三角形. (1分)
理由:∵四边形ABCD是正方形,∴AB=BC=CD=DA=4,
∵BE=BC,∴EC=1,BE=3,
∵F为CD的中点,∴DF=FC=2,
∴EF2=12+22=5,AF2=42+22=20,AE2=42+32=25,∴AE2=EF2+AF2,
∴△AEF是直角三角形. (4分)
(2)∠BOF=2∠BAF. (5分)
证明: ∵AE的中点为O,△ABE,△AEF是直角三角形,
∴AO=BO=OE,OE=OA=OF,∴∠BAO=∠OBA,∠OAF=∠OFA,
∴∠BOF=∠BAO+∠OBA+∠OAF+∠OFA=2∠BAF. (8分)
23.解:(1)四边形AECF是平行四边形. (1分)
理由:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵BE=DF=t,∴EO=FO.
又∵AO=CO,
∴四边形AECF是平行四边形. (5分)
(2)若四边形AECF是矩形,则AC=EF.
当E在BO上时,12=16-2t,解得t=2;
当E有OD上时,12=2t-16,解得t=14.
∴当t=2或14时,四边形AECF为矩形. (10分)
24.解:(1)证明:如图①,连接AC. (1分)
∵四边形ABCD是菱形,∴AB=BC,AB∥CD,CA平分∠BCD.
∵∠B=60°,∴△ABC是等边三角形,
∴∠B=∠BAC=60°,AB=AC.
∵AB∥CD,∴∠ACD=∠BAC=60°,
∴∠B=∠ACD=60°.
∵∠EAF=60°,∴∠BAE+∠EAC=∠EAC+∠CAF=60°,∴∠BAE=∠CAF.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),∴AE=AF,
∴△AEF为等边三角形,∴∠AEF=60°,
∴∠CEF+∠AEB=120°,
∵∠BAE+∠AEB=120°,
∴∠BAE=∠CEF. (6分)
(2)∠BAE=∠CEF. (7分)
证明:如图②,连接AC,由(1)知∠ABC=∠ACD=60°,∠EAF=∠BAC=60°,AB=AC,
∴∠ABE=∠ACF=120°,∠BAE=∠CAF.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),∴AE=AF,
∴△AEF为等边三角形,∴∠AEF=60°,∴∠AEB+∠CEF=60°,
∵∠AEB+∠BAE=∠ABC=60°,
∴∠BAE=∠CEF. (10分)
25.解:(1)GF=GC. (1分)
证明:如图1,连接EG,∵E是BC的中点,∴BE=CE,
∵将△ABE沿AE折叠后得到△AFE,∴BE=EF,∴EF=EC,
∵EG=EG,∠C=∠EFG=90°,∴Rt△ECG≌Rt△EFG(HL),∴FG=CG. (5分)
(2)(1)中的结论仍然成立. (6分)
理由:如图2,连接FC.
∵E是BC的中点,∴BE=CE.
将△ABE沿AE折叠后得到△AFE,∴BE=EF,∠B=∠AFE,∴EF=EC,∴∠EFC=∠ECF.
∵平行四边形ABCD,∴AB∥CD,
∴∠ECD=180°-∠B,∠EFG=180°-∠AFE=180°-∠B,∴∠ECD=∠EFG.
∵∠GFC=∠GFE-∠EFC,∠GCF=∠ECG-∠ECF,∴∠GFC=∠GCF,
∴FG=GC. (12分)
同课章节目录
