月考闯关测试卷(二)(第十六章~第十九章) (含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 月考闯关测试卷(二)(第十六章~第十九章) (含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 250.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:24:30 | ||
图片预览



文档简介
月考测试卷(二)
时间:90分钟 满分:120分 考试范围:第十六章~第十九章
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共30分)
1.若二次根式有意义,则a为 ( )
A.正数 B.负数 C.零 D.任意实数
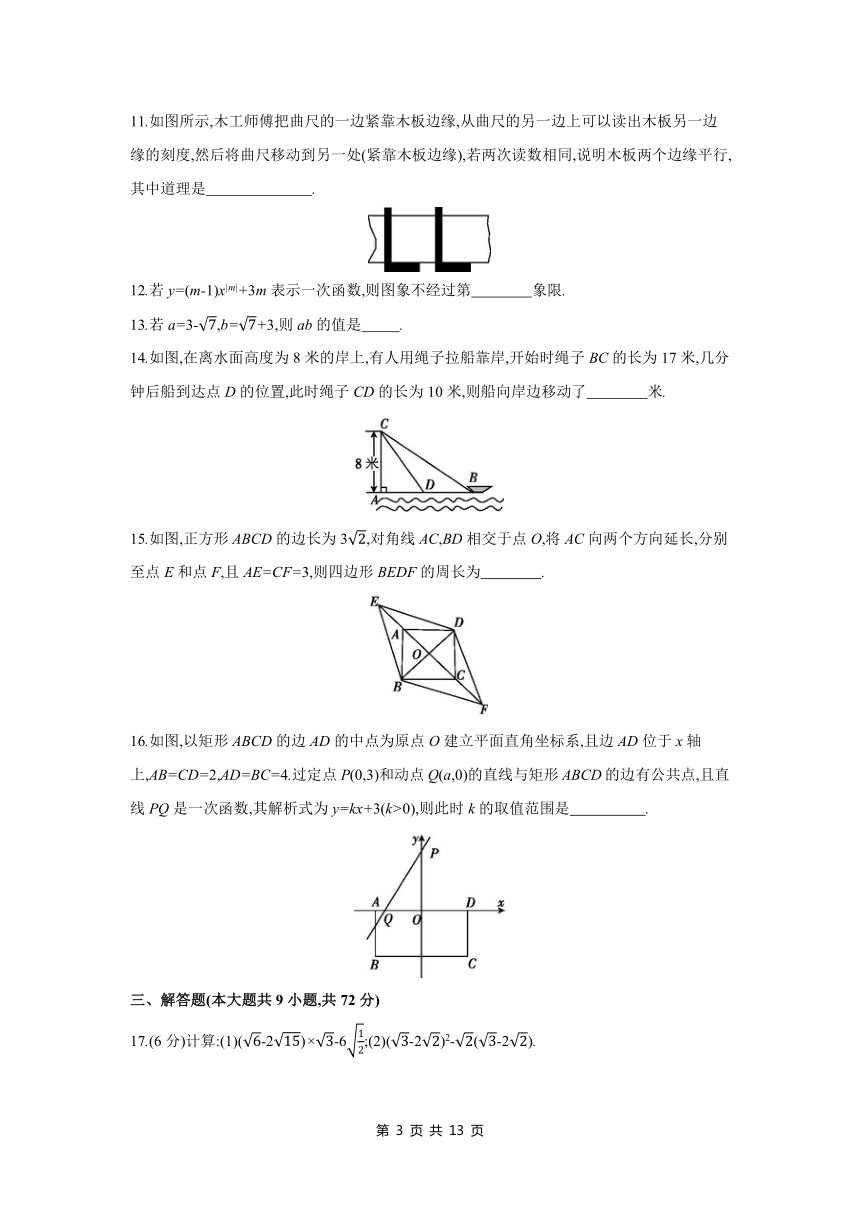
2.下列四个图象中,y不是x的函数图象的是 ( )
3.平行四边形有两个内角之和为50°,则该平行四边形的最大内角度数是 ( )
A.125° B.130° C.155° D.165°
4.如图,在小正方形网格中,△ABC是 ( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
5.在等腰△ABC中,AB=AC,分别延长BA,CA到点D,E,使DA=AB,EA=CA,则四边形BCDE是 ( )
A.任意四边形 B.矩形 C.菱形 D.正方形
6.下列计算正确的是 ( )
A.-= B.=3-1
C.(2-)(2+)=1 D.=-=1
7.已知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④当x>3时,y1A.1 B.2 C.3 D.4
8.小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示.他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为 ( )
A.16米 B.米 C.米 D.8米
9.一天,明明和强强相约到距他们村庄560米的博物馆游玩,他们同时从村庄出发去博物馆,明明到博物馆后因家中有事立即返回.如图,这是他们离村庄的距离y(米)与步行时间x(分钟)之间的函数图象,若他们出发后6分钟相遇,则相遇时强强的速度是 ( )
A.80米/分 B.90米/分 C.100米/分 D.不能确定
10.如图,在矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC=2,则下列结论:①FB⊥OC;②△EOB≌△CMB;③四边形EBFD是菱形;④MB=2.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共18分)
11.如图所示,木工师傅把曲尺的一边紧靠木板边缘,从曲尺的另一边上可以读出木板另一边缘的刻度,然后将曲尺移动到另一处(紧靠木板边缘),若两次读数相同,说明木板两个边缘平行,其中道理是 .
12.若y=(m-1)x|m|+3m表示一次函数,则图象不经过第 象限.
13.若a=3-,b=+3,则ab的值是 .
14.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了 米.
15.如图,正方形ABCD的边长为3,对角线AC,BD相交于点O,将AC向两个方向延长,分别至点E和点F,且AE=CF=3,则四边形BEDF的周长为 .
16.如图,以矩形ABCD的边AD的中点为原点O建立平面直角坐标系,且边AD位于x轴上,AB=CD=2,AD=BC=4.过定点P(0,3)和动点Q(a,0)的直线与矩形ABCD的边有公共点,且直线PQ是一次函数,其解析式为y=kx+3(k>0),则此时k的取值范围是 .
三、解答题(本大题共9小题,共72分)
17.(6分)计算:(1)(-2)×-6;(2)(-2)2-(-2).
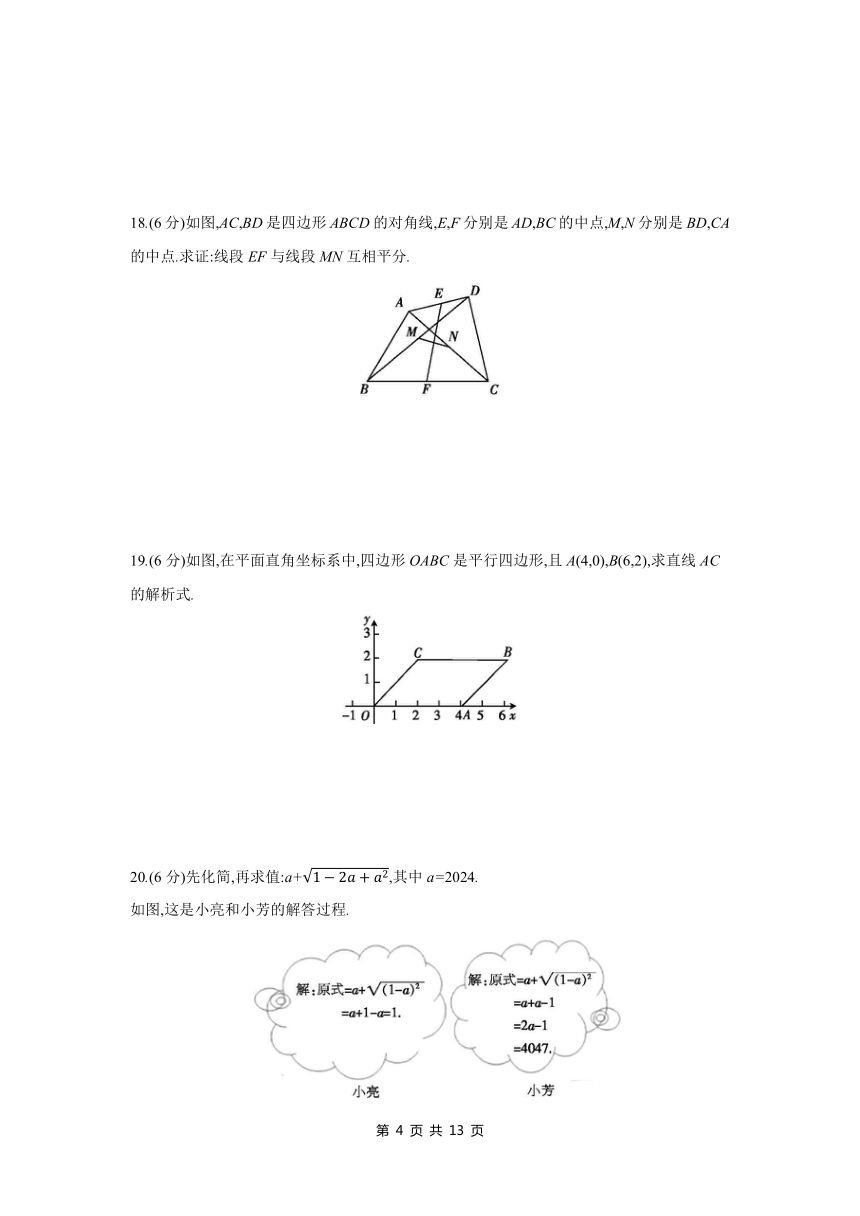
18.(6分)如图,AC,BD是四边形ABCD的对角线,E,F分别是AD,BC的中点,M,N分别是BD,CA的中点.求证:线段EF与线段MN互相平分.
19.(6分)如图,在平面直角坐标系中,四边形OABC是平行四边形,且A(4,0),B(6,2),求直线AC的解析式.
20.(6分)先化简,再求值:a+,其中a=2024.
如图,这是小亮和小芳的解答过程.
(1) 的解法是错误的,错误的原因在于未能正确地运用二次根式的性质: .
(2)先化简,再求值:a+2,其中a=-2.
21.(8分)如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)试判断△CHB是否为直角三角形,并说明理由.
(2)新路CH比原路CA少多少千米
22.(8分)如图,在面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
(1)求证:四边形AEFD是菱形.
(2)求四边形AEFD的两条对角线的长.
23.(10分)如图,E是矩形ABCD边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为点F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形 请予以证明.
(2)在(1)中,动点P运动到什么位置时,矩形PHEF变为正方形 请说明理由.
24.(10分)某健身馆普通票价为40元/张,6~9月为了促销,新推出两种优惠卡:
①金卡售价1200元/张,每次凭卡不再收费;
②银卡售价300元/张,每次凭卡另收10元.
普通票正常出售,两种优惠卡仅限6~9月使用,不限次数.设健身x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A,B,C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
25.(12分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE.
(2)求∠CPE的度数.
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
C A C D B B C D A B
1.C 【解析】由题意,得-a2≥0,解得a=0.
2.A 【解析】选项B,C,D中对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应,所以y是x的函数;而A中的y的值不具有唯一性,所以不是函数图象.
3.C 【解析】∵平行四边形有两个内角之和为50°,∴这组对角都等于25°,∴另外两个角都为180°-25°=155°,∴这个平行四边形的最大内角为155°.
4.D 【解析】设小正方形的边长是1,则AB=,BC=,AC=2,∴AB2+AC2=BC2,∴△ABC是直角三角形.
5.B 【解析】如图所示,∵AC=AE,AB=AD,∴四边形BCDE为平行四边形,∵AB=AC,DA=AB,EA=CA,∴BD=CE,∴四边形BCDE为矩形.
6.B 【解析】-=2-=;===3-1;(2-)(2+)=4-5=-1;==.
7.C 【解析】根据根据图象得①③④正确;∵a<0,∴②错误.
8.D 【解析】如图,AC=5+3=8,BC=8,在Rt△ABC中,AB===8.即从点A攀爬到点B的最短路径为8米.
9.A 【解析】观察图象可得出:点A的坐标为(5,560),点B的坐标为(12,0),设线段AB的解析式为y=kx+b(k≠0),∴,解得,∴线段AB的解析式为y=-80x+960(5≤x≤12).当x=6时,y=480,∴点F的坐标为(6,480),∴所以相遇时强强的速度是480÷6=80(米/分).
10.B 【解析】如图,连接BD,∵四边形ABCD是矩形,∴AC=BD,AC,BD互相平分,∵O为AC中点,∴BD也过O点,∴OB=OC,∵∠COB=60°,OB=OC,∴△OBC是等边三角形,∴OB=BC=OC,∠OBC=60°,在△OBF与△CBF中,,∴△OBF≌△CBF(SSS),∴△OBF与△CBF关于直线BF对称,∴FB⊥OC,OM=CM,①正确;∵∠OBC=60°,∴∠ABO=30°,∵△OBF≌△CBF,∴∠OBM=∠CBM=30°,∴∠ABO=∠OBF,∵AB∥CD,∴∠OCF=∠OAE,∵OA=OC,∠AOE=∠FOC,∴△AOE≌△COF(ASA),∴OE=OF,∴OB⊥EF,∴四边形EBFD是菱形,③正确,∵△EOB≌△FOB≌△FCB,∴△EOB≌△CMB错误,②错误;∵FO=FC=2,FM⊥OC,∠FCM=30°,∴CM=,∵∠CBM=30°,∴BC=2,∴BM=3,④错误.
二、填空题
11 12 13 14 15 16
平行四边形 的对边平行 一 2 9 12 k≥
11.平行四边形的对边平行 【解析】根据题意,得AB=CD,AB∥CD,∴四边形ABCD是平行四边形,∴AD∥BC.
12.一 【解析】由题意,得|m|=1且m-1≠0 ,解得m=-1,所以一次函数解析式为y=-2x-3,该图象不经过第一象限.
13.2 【解析】ab=(3-)(+3)=9-7=2.
14.9 【解析】在Rt△ABC中,∵∠CAB=90°,BC=17米,AC=8米,∴AB===15(米),∵CD=10(米),∴AD===6(米),∴BD=AB-AD=15-6=9(米),所以船向岸边移动了9米.
15.12 【解析】∵四边形ABCD为正方形,∴AC⊥BD,∵正方形ABCD的边长为3,∴AC=BD===6,∴OA=OB=OC=OD=3,∵AE=CF=3,∴OE=OF=6,∴四边形BEDF为菱形,∴BE==3,则四边形BEDF的周长为4×3=12.
16. k≥ 【解析】∵k>0,∴PQ经过第一、三象限.当点Q与点A重合时,则点Q的坐标为(-2,0),代入函数解析式y=kx+3中,得k=,即当k的取值范围为k≥时,PQ在第二、三象限与长方形ABCD有交点.
三、解答题
17.解:(1)原式=3-6-3=-6; (3分)
(2)原式=3-4+8-+4=15-5. (6分)
18.证明:如图,连接ME,MF,NE,NF,
∵E,M分别是AD,BD的中点,
∴ME是△ABD的中位线,∴ME∥AB, (3分)
同理:MF∥CD,EN∥CD,FN∥AB,
∴ME∥FN,MF∥EN,
∴四边形EMFN是平行四边形,
∴线段EF与线段MN互相平分. (6分)
19.解:∵四边形OABC是平行四边形,∴OA∥BC,OA=BC,∵A(4,0),B(6,2),∴C(2,2), (2分)
设直线AC的解析式为y=kx+b,
∴,解得,
∴直线AC的解析式为y=-x+4. (6分)
20.解:(1)小亮 =|a| (2分)
(2)原式=a+2=a+2|a-3|,
∵a=-2<3,∴a-3<0.
∴原式=a+2(3-a)=a+6-2a=6-a.
将a=-2代入,得6-(-2)=8. (6分)
21.解:(1)是. (1分)
理由:在△CHB中,∵CH2+BH2=(1.2)2+(0.9)2=2.25,BC2=2.25,∴CH2+BH2=BC2,∴△CHB是直角三角形. (4分)
(2)设AC=x千米,则根据题意,得AH=x-0.9,CH=1.2,在Rt△ACH中,AC2=AH2+CH2,∴x2=(x-0.9)2+1.22,解得x=1.25,1.25-1.2=0.05(千米).
答:新路CH比原路CA少0.05千米. (8分)
22.解:(1)证明:由平移,得AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
又∵AE=AD=5,
∴四边形AEFD是菱形. (3分)
(2)根据题意,得AB·AD=15,解得AB=3.
在Rt△ABE中,AB=3,AE=5,
则BE==4.
如图,连接AF,ED,
在Rt△ABF中,
AF=
==3;
在Rt△DCE中,
DE==. (8分)
23.解:(1)AD=2AB. (1分)
证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD.
∵E是BC的中点,∴AB=BE=EC=CD,∴△ABE,△DCE是等腰直角三角形,
∴∠AEB=∠DEC=45°,∴∠AED=90°.
∵PF⊥AE,PH⊥DE,∴∠PFE=∠EHP=90°.
在四边形PFEH中,∠PFE=∠FEH=∠EHP=90°,故四边形PFEH是矩形. (5分)
(2)点P是AD的中点时,矩形PHEF变为正方形. (6分)
理由:由(1)可得∠BAE=∠CDE=45°,
∴∠FAP=∠HDP=45°.
又∵∠AFP=∠PHD=90°,AP=PD,
∴△AFP≌△DHP,∴PF=PH.
在矩形PFEH中,PF=PH,故矩形PFEH是正方形. (10分)
24.解:(1)银卡消费:y=10x+300; (1分)
普通票消费:y=40x. (2分)
(2)令y=10x+300中的x=0,则y=300,故点A的坐标为(0,300); (4分)
联立,解得,
故点B的坐标为(10,400); (6分)
将y=1200代入y=10x+300,解得x=90,
故点C的坐标为(90,1200). (8分)
(3)根据函数图象可知:当090时,选择购买金卡更合算. (10分)
25.解:(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°.
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∵PA=PE,∴PC=PE. (3分)
(2)由(1)可知△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP.
∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E.
∵∠CFP=∠EFD,
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,即∠CPF=∠EDF=90°. (6分)
(3)AP=CE. (7分)
理由:在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°.
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP.
∵PA=PE,∴PC=PE,∴∠DAP=∠DCP,∠DAP=∠AEP,∴∠DCP=∠AEP.
∵∠CFP=∠EFD,
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,∴PC=CE,∴AP=CE. (12分)
时间:90分钟 满分:120分 考试范围:第十六章~第十九章
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共30分)
1.若二次根式有意义,则a为 ( )
A.正数 B.负数 C.零 D.任意实数
2.下列四个图象中,y不是x的函数图象的是 ( )
3.平行四边形有两个内角之和为50°,则该平行四边形的最大内角度数是 ( )
A.125° B.130° C.155° D.165°
4.如图,在小正方形网格中,△ABC是 ( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
5.在等腰△ABC中,AB=AC,分别延长BA,CA到点D,E,使DA=AB,EA=CA,则四边形BCDE是 ( )
A.任意四边形 B.矩形 C.菱形 D.正方形
6.下列计算正确的是 ( )
A.-= B.=3-1
C.(2-)(2+)=1 D.=-=1
7.已知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③关于x的方程kx+b=x+a的解为x=3;④当x>3时,y1
8.小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示.他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为 ( )
A.16米 B.米 C.米 D.8米
9.一天,明明和强强相约到距他们村庄560米的博物馆游玩,他们同时从村庄出发去博物馆,明明到博物馆后因家中有事立即返回.如图,这是他们离村庄的距离y(米)与步行时间x(分钟)之间的函数图象,若他们出发后6分钟相遇,则相遇时强强的速度是 ( )
A.80米/分 B.90米/分 C.100米/分 D.不能确定
10.如图,在矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC=2,则下列结论:①FB⊥OC;②△EOB≌△CMB;③四边形EBFD是菱形;④MB=2.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共18分)
11.如图所示,木工师傅把曲尺的一边紧靠木板边缘,从曲尺的另一边上可以读出木板另一边缘的刻度,然后将曲尺移动到另一处(紧靠木板边缘),若两次读数相同,说明木板两个边缘平行,其中道理是 .
12.若y=(m-1)x|m|+3m表示一次函数,则图象不经过第 象限.
13.若a=3-,b=+3,则ab的值是 .
14.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了 米.
15.如图,正方形ABCD的边长为3,对角线AC,BD相交于点O,将AC向两个方向延长,分别至点E和点F,且AE=CF=3,则四边形BEDF的周长为 .
16.如图,以矩形ABCD的边AD的中点为原点O建立平面直角坐标系,且边AD位于x轴上,AB=CD=2,AD=BC=4.过定点P(0,3)和动点Q(a,0)的直线与矩形ABCD的边有公共点,且直线PQ是一次函数,其解析式为y=kx+3(k>0),则此时k的取值范围是 .
三、解答题(本大题共9小题,共72分)
17.(6分)计算:(1)(-2)×-6;(2)(-2)2-(-2).
18.(6分)如图,AC,BD是四边形ABCD的对角线,E,F分别是AD,BC的中点,M,N分别是BD,CA的中点.求证:线段EF与线段MN互相平分.
19.(6分)如图,在平面直角坐标系中,四边形OABC是平行四边形,且A(4,0),B(6,2),求直线AC的解析式.
20.(6分)先化简,再求值:a+,其中a=2024.
如图,这是小亮和小芳的解答过程.
(1) 的解法是错误的,错误的原因在于未能正确地运用二次根式的性质: .
(2)先化简,再求值:a+2,其中a=-2.
21.(8分)如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)试判断△CHB是否为直角三角形,并说明理由.
(2)新路CH比原路CA少多少千米
22.(8分)如图,在面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
(1)求证:四边形AEFD是菱形.
(2)求四边形AEFD的两条对角线的长.
23.(10分)如图,E是矩形ABCD边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为点F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形 请予以证明.
(2)在(1)中,动点P运动到什么位置时,矩形PHEF变为正方形 请说明理由.
24.(10分)某健身馆普通票价为40元/张,6~9月为了促销,新推出两种优惠卡:
①金卡售价1200元/张,每次凭卡不再收费;
②银卡售价300元/张,每次凭卡另收10元.
普通票正常出售,两种优惠卡仅限6~9月使用,不限次数.设健身x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A,B,C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
25.(12分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE.
(2)求∠CPE的度数.
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
C A C D B B C D A B
1.C 【解析】由题意,得-a2≥0,解得a=0.
2.A 【解析】选项B,C,D中对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应,所以y是x的函数;而A中的y的值不具有唯一性,所以不是函数图象.
3.C 【解析】∵平行四边形有两个内角之和为50°,∴这组对角都等于25°,∴另外两个角都为180°-25°=155°,∴这个平行四边形的最大内角为155°.
4.D 【解析】设小正方形的边长是1,则AB=,BC=,AC=2,∴AB2+AC2=BC2,∴△ABC是直角三角形.
5.B 【解析】如图所示,∵AC=AE,AB=AD,∴四边形BCDE为平行四边形,∵AB=AC,DA=AB,EA=CA,∴BD=CE,∴四边形BCDE为矩形.
6.B 【解析】-=2-=;===3-1;(2-)(2+)=4-5=-1;==.
7.C 【解析】根据根据图象得①③④正确;∵a<0,∴②错误.
8.D 【解析】如图,AC=5+3=8,BC=8,在Rt△ABC中,AB===8.即从点A攀爬到点B的最短路径为8米.
9.A 【解析】观察图象可得出:点A的坐标为(5,560),点B的坐标为(12,0),设线段AB的解析式为y=kx+b(k≠0),∴,解得,∴线段AB的解析式为y=-80x+960(5≤x≤12).当x=6时,y=480,∴点F的坐标为(6,480),∴所以相遇时强强的速度是480÷6=80(米/分).
10.B 【解析】如图,连接BD,∵四边形ABCD是矩形,∴AC=BD,AC,BD互相平分,∵O为AC中点,∴BD也过O点,∴OB=OC,∵∠COB=60°,OB=OC,∴△OBC是等边三角形,∴OB=BC=OC,∠OBC=60°,在△OBF与△CBF中,,∴△OBF≌△CBF(SSS),∴△OBF与△CBF关于直线BF对称,∴FB⊥OC,OM=CM,①正确;∵∠OBC=60°,∴∠ABO=30°,∵△OBF≌△CBF,∴∠OBM=∠CBM=30°,∴∠ABO=∠OBF,∵AB∥CD,∴∠OCF=∠OAE,∵OA=OC,∠AOE=∠FOC,∴△AOE≌△COF(ASA),∴OE=OF,∴OB⊥EF,∴四边形EBFD是菱形,③正确,∵△EOB≌△FOB≌△FCB,∴△EOB≌△CMB错误,②错误;∵FO=FC=2,FM⊥OC,∠FCM=30°,∴CM=,∵∠CBM=30°,∴BC=2,∴BM=3,④错误.
二、填空题
11 12 13 14 15 16
平行四边形 的对边平行 一 2 9 12 k≥
11.平行四边形的对边平行 【解析】根据题意,得AB=CD,AB∥CD,∴四边形ABCD是平行四边形,∴AD∥BC.
12.一 【解析】由题意,得|m|=1且m-1≠0 ,解得m=-1,所以一次函数解析式为y=-2x-3,该图象不经过第一象限.
13.2 【解析】ab=(3-)(+3)=9-7=2.
14.9 【解析】在Rt△ABC中,∵∠CAB=90°,BC=17米,AC=8米,∴AB===15(米),∵CD=10(米),∴AD===6(米),∴BD=AB-AD=15-6=9(米),所以船向岸边移动了9米.
15.12 【解析】∵四边形ABCD为正方形,∴AC⊥BD,∵正方形ABCD的边长为3,∴AC=BD===6,∴OA=OB=OC=OD=3,∵AE=CF=3,∴OE=OF=6,∴四边形BEDF为菱形,∴BE==3,则四边形BEDF的周长为4×3=12.
16. k≥ 【解析】∵k>0,∴PQ经过第一、三象限.当点Q与点A重合时,则点Q的坐标为(-2,0),代入函数解析式y=kx+3中,得k=,即当k的取值范围为k≥时,PQ在第二、三象限与长方形ABCD有交点.
三、解答题
17.解:(1)原式=3-6-3=-6; (3分)
(2)原式=3-4+8-+4=15-5. (6分)
18.证明:如图,连接ME,MF,NE,NF,
∵E,M分别是AD,BD的中点,
∴ME是△ABD的中位线,∴ME∥AB, (3分)
同理:MF∥CD,EN∥CD,FN∥AB,
∴ME∥FN,MF∥EN,
∴四边形EMFN是平行四边形,
∴线段EF与线段MN互相平分. (6分)
19.解:∵四边形OABC是平行四边形,∴OA∥BC,OA=BC,∵A(4,0),B(6,2),∴C(2,2), (2分)
设直线AC的解析式为y=kx+b,
∴,解得,
∴直线AC的解析式为y=-x+4. (6分)
20.解:(1)小亮 =|a| (2分)
(2)原式=a+2=a+2|a-3|,
∵a=-2<3,∴a-3<0.
∴原式=a+2(3-a)=a+6-2a=6-a.
将a=-2代入,得6-(-2)=8. (6分)
21.解:(1)是. (1分)
理由:在△CHB中,∵CH2+BH2=(1.2)2+(0.9)2=2.25,BC2=2.25,∴CH2+BH2=BC2,∴△CHB是直角三角形. (4分)
(2)设AC=x千米,则根据题意,得AH=x-0.9,CH=1.2,在Rt△ACH中,AC2=AH2+CH2,∴x2=(x-0.9)2+1.22,解得x=1.25,1.25-1.2=0.05(千米).
答:新路CH比原路CA少0.05千米. (8分)
22.解:(1)证明:由平移,得AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
又∵AE=AD=5,
∴四边形AEFD是菱形. (3分)
(2)根据题意,得AB·AD=15,解得AB=3.
在Rt△ABE中,AB=3,AE=5,
则BE==4.
如图,连接AF,ED,
在Rt△ABF中,
AF=
==3;
在Rt△DCE中,
DE==. (8分)
23.解:(1)AD=2AB. (1分)
证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD.
∵E是BC的中点,∴AB=BE=EC=CD,∴△ABE,△DCE是等腰直角三角形,
∴∠AEB=∠DEC=45°,∴∠AED=90°.
∵PF⊥AE,PH⊥DE,∴∠PFE=∠EHP=90°.
在四边形PFEH中,∠PFE=∠FEH=∠EHP=90°,故四边形PFEH是矩形. (5分)
(2)点P是AD的中点时,矩形PHEF变为正方形. (6分)
理由:由(1)可得∠BAE=∠CDE=45°,
∴∠FAP=∠HDP=45°.
又∵∠AFP=∠PHD=90°,AP=PD,
∴△AFP≌△DHP,∴PF=PH.
在矩形PFEH中,PF=PH,故矩形PFEH是正方形. (10分)
24.解:(1)银卡消费:y=10x+300; (1分)
普通票消费:y=40x. (2分)
(2)令y=10x+300中的x=0,则y=300,故点A的坐标为(0,300); (4分)
联立,解得,
故点B的坐标为(10,400); (6分)
将y=1200代入y=10x+300,解得x=90,
故点C的坐标为(90,1200). (8分)
(3)根据函数图象可知:当0
25.解:(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°.
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∵PA=PE,∴PC=PE. (3分)
(2)由(1)可知△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP.
∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E.
∵∠CFP=∠EFD,
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,即∠CPF=∠EDF=90°. (6分)
(3)AP=CE. (7分)
理由:在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°.
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP.
∵PA=PE,∴PC=PE,∴∠DAP=∠DCP,∠DAP=∠AEP,∴∠DCP=∠AEP.
∵∠CFP=∠EFD,
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,∴PC=CE,∴AP=CE. (12分)
同课章节目录
