月考闯关测试卷(一)(第十六章~第十七章)(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 月考闯关测试卷(一)(第十六章~第十七章)(含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:24:49 | ||
图片预览



文档简介
月考测试卷(一)
时间:90分钟 满分:120分 考试范围:第十六章~第十七章
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共30分)
1.下列式子中,是二次根式的是 ( )
A. B. C. D.
2.若有意义,则x的取值范围是 ( )
A.x≥-2 B.x≠2 C.x≥1且x≠2 D.x≥-1
3.下列二次根式中,是最简二次根式的是 ( )
A. B. C. D.
4.下列四组数:①0.3,0.4,0.5;②32,42,52;③3,4,5;④,,.其中不是勾股数的有 ( )
A.1组 B.2组 C.3组 D.4组
5.下列各式中,运算正确的是 ( )
A.2+=2 B.-=2
C.5-3=2 D.-=
6.下列等式成立的是 ( )
A.(-7)2=2 B.-5=-2
C.÷=4 D.4×2=8
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=10.5,大正方形的面积为48,则小正方形的面积为 ( )
A.8 B.16 C.25 D.27
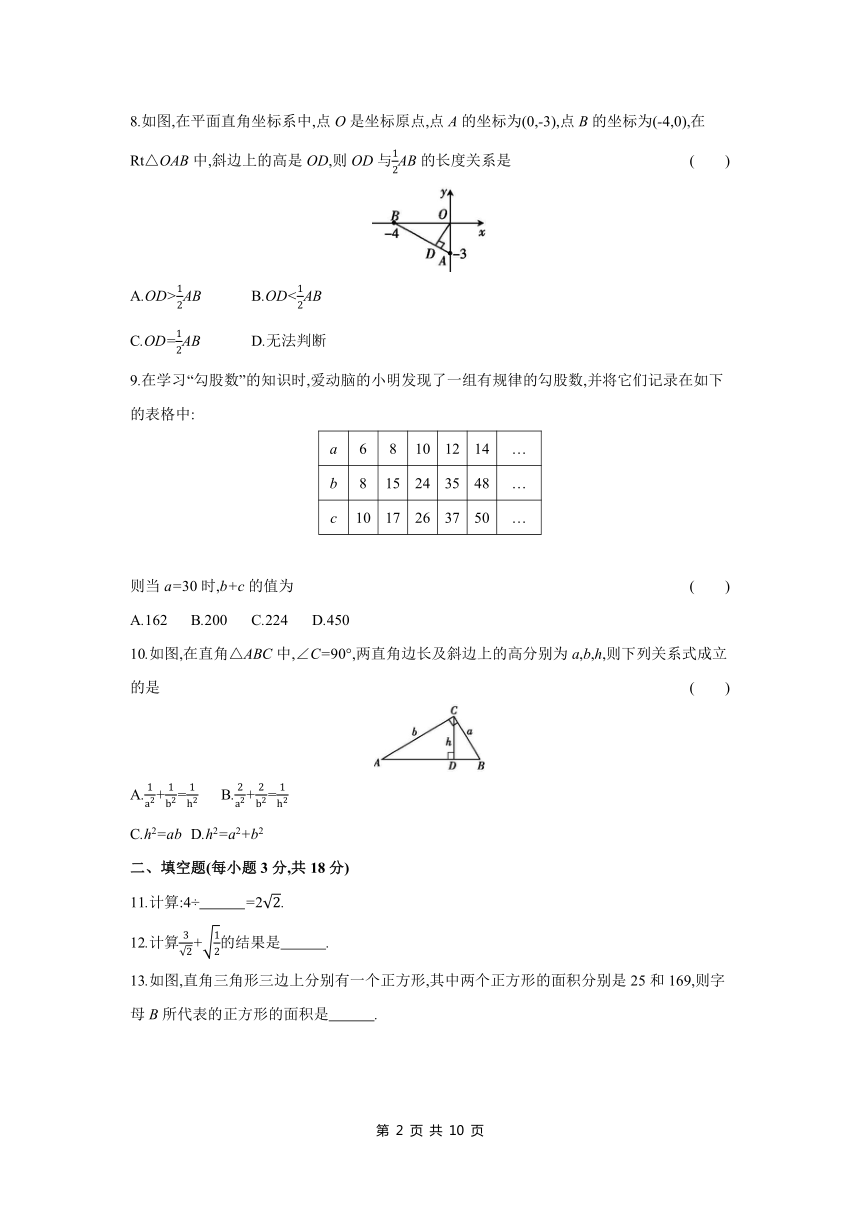
8.如图,在平面直角坐标系中,点O是坐标原点,点A的坐标为(0,-3),点B的坐标为(-4,0),在Rt△OAB中,斜边上的高是OD,则OD与AB的长度关系是 ( )
A.OD>AB B.ODC.OD=AB D.无法判断
9.在学习“勾股数”的知识时,爱动脑的小明发现了一组有规律的勾股数,并将它们记录在如下的表格中:
a 6 8 10 12 14 …
b 8 15 24 35 48 …
c 10 17 26 37 50 …
则当a=30时,b+c的值为 ( )
A.162 B.200 C.224 D.450
10.如图,在直角△ABC中,∠C=90°,两直角边长及斜边上的高分别为a,b,h,则下列关系式成立的是 ( )
A.+= B.+=
C.h2=ab D.h2=a2+b2
二、填空题(每小题3分,共18分)
11.计算:4÷ =2.
12.计算+的结果是 .
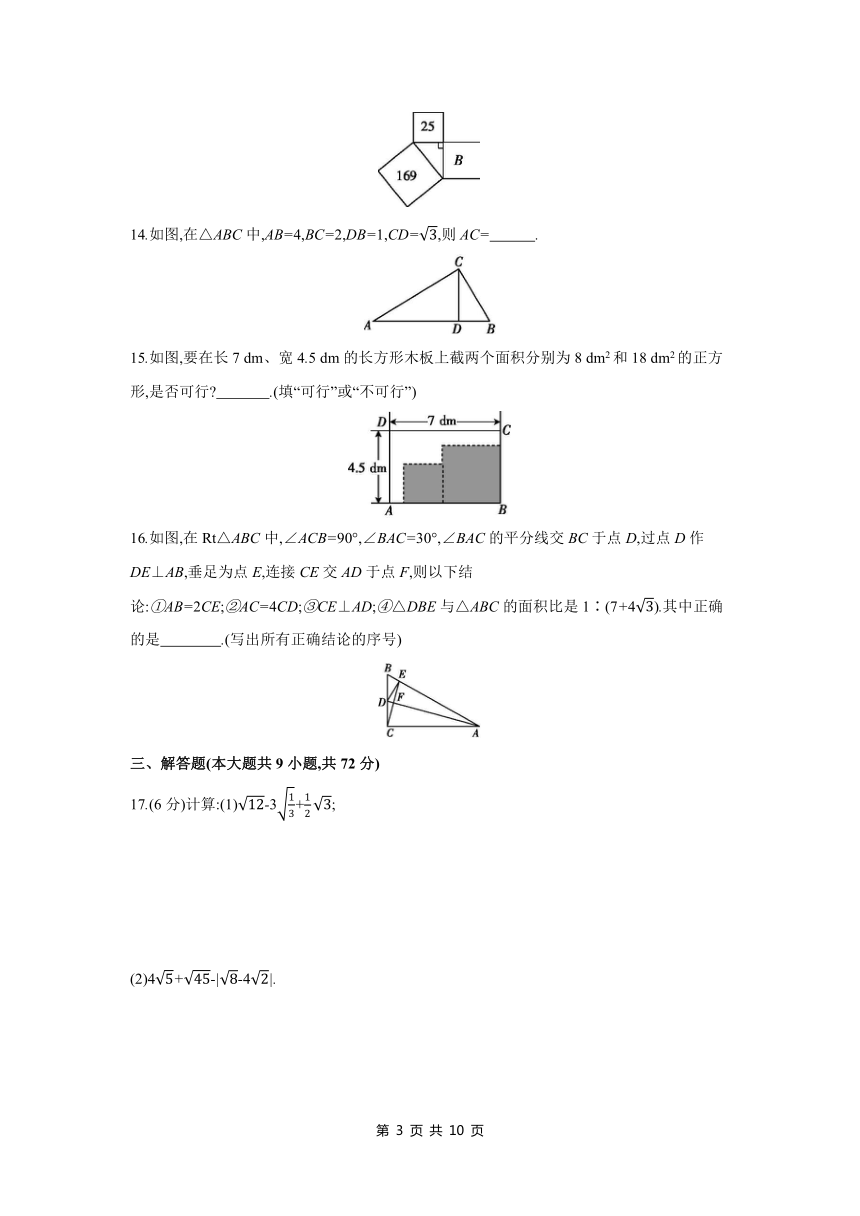
13.如图,直角三角形三边上分别有一个正方形,其中两个正方形的面积分别是25和169,则字母B所代表的正方形的面积是 .
14.如图,在△ABC中,AB=4,BC=2,DB=1,CD=,则AC= .
15.如图,要在长7 dm、宽4.5 dm的长方形木板上截两个面积分别为8 dm2和18 dm2的正方形,是否可行 .(填“可行”或“不可行”)
16.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠BAC的平分线交BC于点D,过点D作DE⊥AB,垂足为点E,连接CE交AD于点F,则以下结论:①AB=2CE;②AC=4CD;③CE⊥AD;④△DBE与△ABC的面积比是1∶(7+4).其中正确的是 .(写出所有正确结论的序号)
三、解答题(本大题共9小题,共72分)
17.(6分)计算:(1)-3+;
(2)4+-|-4|.
18.(6分)说出下列命题的逆命题,并判断这些逆命题是否成立.
(1)如果两个角是锐角,那么这两个角相等;
(2)全等三角形的对应边相等;
(3)线段垂直平分线上的点到线段两端的距离相等.
19.(6分)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根四尺,问折者高几何 ”翻译成数学问题:如图所示,在△ABC中,∠ACB=90°,AC+AB=10,BC=4,求AC的长.
20.(6分)若x,y为实数,且满足y=+-3,求x+2y的值.
21.(8分)已知a=7-2,b=7+2.
(1)求ab的值;
(2)求a2+b2+3ab的值.
22.(8分)如图,已知等腰△ABC的底边BC=20 cm,D是腰AB上的一点,且BD=12 cm,CD=16 cm.
(1)求证:△BCD是直角三角形.
(2)求△ABC的周长.
23.(10分)小明在解决问题“已知a=,求2a2-8a+1的值”时,他是这样分析与解答的:∵a===2-,∴a-2=-,
∴(a-2)2=3,a2-4a+4=3,∴a2-4a=-1,
∴2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决下列问题:
(1)化简:+++…+.
(2)若a=,求4a2-8a+1的值.
24.(10分)阅读下列内容:设a,b,c是一个三角形的三条边的长,且c是最长边,我们可以利用a,b,c三边长间的关系来判断这个三角形的形状:
①若c2=a2+b2,则该三角形是直角三角形;
②若c2>a2+b2,则该三角形是钝角三角形;
③若c2例如:一个三角形的三边长分别是4,5,6,则最长边是6,由于62=36<42+52,故知该三角形是锐角三角形.
请解答以下问题:
(1)若一个三角形的三条边长分别是2,3,4,请判断该三角形的形状;
(2)若一个三角形的三条边长分别是3,4,x,且这个三角形是直角三角形,求出x的值;
(3)若一个三角形的三条边长a=,b=,c=,其中a是最长边,请判断这个三角形的形状,并写出你的判断过程.
25.(12分)如图,在△ABC中,∠ACB=90°,AB=10,BC=6,若点P从点A出发,以每秒1个单位长度的速度沿折线A-C-B-A运动,设运动时间为t(t>0)秒.
(1)若点P在AC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠BAC的平分线上,求此时t的值.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
B D A C C B D B D A
1.B 【解析】A选项的被开方数正负不确定,C选项的被开方数是负数,D选项的根指数是3,它们都不符合二次根式的定义,只有a2+>0,故B选项是二次根式.
2.D 【解析】由题意,得x+1≥0且x+2≠0,解得x≥-1.
3.A 【解析】根据最简二次根式的定义,可知是最简二次根式.
4.C 【解析】勾股数是正整数,故①④都不是勾股数;又(32)2+(42)2≠(52)2,故32,42,52不是勾股数.∵32+42=52,∴3,4,5是一组勾股数.
6.B 【解析】(-7)2=49×=14,故A错误;-5=-5×=-2,故B正确;÷=2,故C错误;4×2=40,故D错误.
7.D 【解析】由题意,得,∴小正方形的面积=(a-b)2=a2+b2-2ab=48-21=27.
8.B 【解析】由勾股定理,可求得AB=5,则AB=2.5.由题意,知×3×4=×5×OD,解得OD=2.4.∵2.5>2.4,∴OD9.D 【解析】根据表格中数据可得a2+b2=c2,并且c=b+2,则a2+b2=(b+2)2.当a=30时,302+b2=(b+2)2,解得b=224.则c=224+2=226,∴b+c=224+226=450.
10.A 【解析】设斜边为c,根据勾股定理得出c=.∵ab=ch,∴ab=·h,即a2b2=a2h2+b2h2,∴=+,即+=.
二、填空题
11 12 13 14 15 16
2 144 2 不可行 ③④
11. 【解析】空格为4÷2=2÷=.
12.2 【解析】原式=+=2.
13.144 【解析】由勾股定理得字母B所代表的正方形的面积=169-25=144.
14.2 【解析】∵BC=2,DB=1,CD=,∴DB2+CD2=1+3=4=BC2,∴△CDB是直角三角形,∠CDB=90°,∴∠CDA=90°,∵AB=4,BD=1,∴AD=3,∴AC===2.
15.不可行 【解析】+=5,由于>1.4,可知5>5×1.4=7,即若截两个面积分别为8 dm2和18 dm2的正方形,木板的长不够.
16.③④ 【解析】设BE=a.在Rt△BDE中,∵∠DEB=90°,∠B=60°,BE=a,∴BD=2BE=2a,DE=a.∵DA平分∠CAB,DC⊥AC,DE⊥AB,∴DC=DE=a,∴AB=2BC=4a+2a.∵∠BEC是钝角,∴BC>CE,∵AB=2BC,∴AB>2CE,故①错误;∵△DAC≌△DAE,∴AC=AE=BC=(2a+a)=2a+3a.∵CD=a,∴AC≠4CD,故②错误;∵DE=DC,AC=AE,∴AD垂直平分线段EC,故③正确;∵=
=,
故④正确.
三、解答题
17.解:(1)原式=2-+=; (3分)
(2)∵=2<4,∴-4<0,
∴|-4|=-(-4),
∴原式=4+3+(-4)=7+2-4=7-2. (6分)
18.解:(1)逆命题:如果两个角相等,那么这两个角是锐角.不成立. (2分)
(2)逆命题:对应边相等的三角形是全等三角形.成立. (4分)
(3)逆命题:到线段两端距离相等的点在线段的垂直平分线上.成立. (6分)
19.解:∵在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2.
∵AC+AB=10,BC=4,
设AC=x,则AB=10-x,
∴x2+42=(10-x)2,解得x=.
∴AC的长为. (6分)
20.解:由二次根式有意义的条件,得,
即x2-4=0,解得x=±2. (3分)
当x=±2时,y=-3.
①当x=2,y=-3时,x+2y=2+2×(-3)=-4;
②当x=-2,y=-3时,x+2y=-2+2×(-3)=-8.
∴x+2y的值是-4或-8. (6分)
21.解:(1)ab=(7-2)(7+2)=72-(2)2=49-24=25; (4分)
(2)a2+b2+3ab=(a+b)2+ab=(7-2+7+2)2+25=49+25=74. (8分)
22.解:(1)证明:在△BDC中,BC=20 cm,BD=12 cm,CD=16 cm.
∴BD2+CD2=BC2, (3分)
∴∠BDC=90°,∴△BCD是直角三角形. (4分)
(2)设AB=AC=x cm,则AD=(x-12)cm,
在Rt△ADC中,由勾股定理,得AD2+CD2=AC2,
即(x-12)2+162=x2,解得x=. (6分)
即AB=AC= cm,
∵BC=20 cm,
∴△ABC的周长是AB+AC+BC=++20=(cm). (8分)
23.解:(1)原式=(-1)+(-)+(-)+…+(-)
=-1=10-1=9; (5分)
(2)a==+1, (7分)
4a2-8a+1=4(a2-2a+1)-3=4(a-1)2-3.
当a=+1时,原式=4×()2-3=5. (10分)
24.解:(1)∵42=16>22+32,∴该三角形是钝角三角形. (2分)
(2)①若4为最长边,则42=32+x2,解得x=或x=-(舍去); (4分)
②若x为最长边,则x=32+42,得x=5,x=-5(舍去),所以x的值为5或. (6分)
(3)∵a2-b2-c2=x2+3z2-x+y2-2y+=(x-)2+(y-1)2+3z2+>0,
∴a2>b2+c2,∴该三角形是钝角三角形. (10分)
25.解:(1)如图1,PA=PB,在Rt△ACB中,AC===8. (1分)
设AP=t,则PC=8-t,
在Rt△PCB中,根据勾股定理,得(8-t)2+62=t2,解得t=,
即此时t的值为. (4分)
(2)分两种情况:
①如图2所示,点P在BC上时,过点P作PE⊥AB,
则PC=t-8,PB=14-t, (6分)
∵AP平分∠BAC,且PC⊥AC,∴PE=PC.
在△ACP与△AEP中,
,
∴△ACP≌△AEP(AAS). (7分)
∴AE=AC=8,∴BE=2. (8分)
在Rt△PEB中,根据勾股定理,得PE2+EB2=PB2,
即(t-8)2+22=(14-t)2,解得t=. (10分)
②点P又回到A点时,
∵AC+BC+AB=8+6+10=24,∴t=24.
综上所述,点P在∠BAC的平分线上时,t的值为或24. (12分)
时间:90分钟 满分:120分 考试范围:第十六章~第十七章
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共30分)
1.下列式子中,是二次根式的是 ( )
A. B. C. D.
2.若有意义,则x的取值范围是 ( )
A.x≥-2 B.x≠2 C.x≥1且x≠2 D.x≥-1
3.下列二次根式中,是最简二次根式的是 ( )
A. B. C. D.
4.下列四组数:①0.3,0.4,0.5;②32,42,52;③3,4,5;④,,.其中不是勾股数的有 ( )
A.1组 B.2组 C.3组 D.4组
5.下列各式中,运算正确的是 ( )
A.2+=2 B.-=2
C.5-3=2 D.-=
6.下列等式成立的是 ( )
A.(-7)2=2 B.-5=-2
C.÷=4 D.4×2=8
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=10.5,大正方形的面积为48,则小正方形的面积为 ( )
A.8 B.16 C.25 D.27
8.如图,在平面直角坐标系中,点O是坐标原点,点A的坐标为(0,-3),点B的坐标为(-4,0),在Rt△OAB中,斜边上的高是OD,则OD与AB的长度关系是 ( )
A.OD>AB B.OD
9.在学习“勾股数”的知识时,爱动脑的小明发现了一组有规律的勾股数,并将它们记录在如下的表格中:
a 6 8 10 12 14 …
b 8 15 24 35 48 …
c 10 17 26 37 50 …
则当a=30时,b+c的值为 ( )
A.162 B.200 C.224 D.450
10.如图,在直角△ABC中,∠C=90°,两直角边长及斜边上的高分别为a,b,h,则下列关系式成立的是 ( )
A.+= B.+=
C.h2=ab D.h2=a2+b2
二、填空题(每小题3分,共18分)
11.计算:4÷ =2.
12.计算+的结果是 .
13.如图,直角三角形三边上分别有一个正方形,其中两个正方形的面积分别是25和169,则字母B所代表的正方形的面积是 .
14.如图,在△ABC中,AB=4,BC=2,DB=1,CD=,则AC= .
15.如图,要在长7 dm、宽4.5 dm的长方形木板上截两个面积分别为8 dm2和18 dm2的正方形,是否可行 .(填“可行”或“不可行”)
16.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠BAC的平分线交BC于点D,过点D作DE⊥AB,垂足为点E,连接CE交AD于点F,则以下结论:①AB=2CE;②AC=4CD;③CE⊥AD;④△DBE与△ABC的面积比是1∶(7+4).其中正确的是 .(写出所有正确结论的序号)
三、解答题(本大题共9小题,共72分)
17.(6分)计算:(1)-3+;
(2)4+-|-4|.
18.(6分)说出下列命题的逆命题,并判断这些逆命题是否成立.
(1)如果两个角是锐角,那么这两个角相等;
(2)全等三角形的对应边相等;
(3)线段垂直平分线上的点到线段两端的距离相等.
19.(6分)《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根四尺,问折者高几何 ”翻译成数学问题:如图所示,在△ABC中,∠ACB=90°,AC+AB=10,BC=4,求AC的长.
20.(6分)若x,y为实数,且满足y=+-3,求x+2y的值.
21.(8分)已知a=7-2,b=7+2.
(1)求ab的值;
(2)求a2+b2+3ab的值.
22.(8分)如图,已知等腰△ABC的底边BC=20 cm,D是腰AB上的一点,且BD=12 cm,CD=16 cm.
(1)求证:△BCD是直角三角形.
(2)求△ABC的周长.
23.(10分)小明在解决问题“已知a=,求2a2-8a+1的值”时,他是这样分析与解答的:∵a===2-,∴a-2=-,
∴(a-2)2=3,a2-4a+4=3,∴a2-4a=-1,
∴2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决下列问题:
(1)化简:+++…+.
(2)若a=,求4a2-8a+1的值.
24.(10分)阅读下列内容:设a,b,c是一个三角形的三条边的长,且c是最长边,我们可以利用a,b,c三边长间的关系来判断这个三角形的形状:
①若c2=a2+b2,则该三角形是直角三角形;
②若c2>a2+b2,则该三角形是钝角三角形;
③若c2
请解答以下问题:
(1)若一个三角形的三条边长分别是2,3,4,请判断该三角形的形状;
(2)若一个三角形的三条边长分别是3,4,x,且这个三角形是直角三角形,求出x的值;
(3)若一个三角形的三条边长a=,b=,c=,其中a是最长边,请判断这个三角形的形状,并写出你的判断过程.
25.(12分)如图,在△ABC中,∠ACB=90°,AB=10,BC=6,若点P从点A出发,以每秒1个单位长度的速度沿折线A-C-B-A运动,设运动时间为t(t>0)秒.
(1)若点P在AC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠BAC的平分线上,求此时t的值.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
B D A C C B D B D A
1.B 【解析】A选项的被开方数正负不确定,C选项的被开方数是负数,D选项的根指数是3,它们都不符合二次根式的定义,只有a2+>0,故B选项是二次根式.
2.D 【解析】由题意,得x+1≥0且x+2≠0,解得x≥-1.
3.A 【解析】根据最简二次根式的定义,可知是最简二次根式.
4.C 【解析】勾股数是正整数,故①④都不是勾股数;又(32)2+(42)2≠(52)2,故32,42,52不是勾股数.∵32+42=52,∴3,4,5是一组勾股数.
6.B 【解析】(-7)2=49×=14,故A错误;-5=-5×=-2,故B正确;÷=2,故C错误;4×2=40,故D错误.
7.D 【解析】由题意,得,∴小正方形的面积=(a-b)2=a2+b2-2ab=48-21=27.
8.B 【解析】由勾股定理,可求得AB=5,则AB=2.5.由题意,知×3×4=×5×OD,解得OD=2.4.∵2.5>2.4,∴OD
10.A 【解析】设斜边为c,根据勾股定理得出c=.∵ab=ch,∴ab=·h,即a2b2=a2h2+b2h2,∴=+,即+=.
二、填空题
11 12 13 14 15 16
2 144 2 不可行 ③④
11. 【解析】空格为4÷2=2÷=.
12.2 【解析】原式=+=2.
13.144 【解析】由勾股定理得字母B所代表的正方形的面积=169-25=144.
14.2 【解析】∵BC=2,DB=1,CD=,∴DB2+CD2=1+3=4=BC2,∴△CDB是直角三角形,∠CDB=90°,∴∠CDA=90°,∵AB=4,BD=1,∴AD=3,∴AC===2.
15.不可行 【解析】+=5,由于>1.4,可知5>5×1.4=7,即若截两个面积分别为8 dm2和18 dm2的正方形,木板的长不够.
16.③④ 【解析】设BE=a.在Rt△BDE中,∵∠DEB=90°,∠B=60°,BE=a,∴BD=2BE=2a,DE=a.∵DA平分∠CAB,DC⊥AC,DE⊥AB,∴DC=DE=a,∴AB=2BC=4a+2a.∵∠BEC是钝角,∴BC>CE,∵AB=2BC,∴AB>2CE,故①错误;∵△DAC≌△DAE,∴AC=AE=BC=(2a+a)=2a+3a.∵CD=a,∴AC≠4CD,故②错误;∵DE=DC,AC=AE,∴AD垂直平分线段EC,故③正确;∵=
=,
故④正确.
三、解答题
17.解:(1)原式=2-+=; (3分)
(2)∵=2<4,∴-4<0,
∴|-4|=-(-4),
∴原式=4+3+(-4)=7+2-4=7-2. (6分)
18.解:(1)逆命题:如果两个角相等,那么这两个角是锐角.不成立. (2分)
(2)逆命题:对应边相等的三角形是全等三角形.成立. (4分)
(3)逆命题:到线段两端距离相等的点在线段的垂直平分线上.成立. (6分)
19.解:∵在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2.
∵AC+AB=10,BC=4,
设AC=x,则AB=10-x,
∴x2+42=(10-x)2,解得x=.
∴AC的长为. (6分)
20.解:由二次根式有意义的条件,得,
即x2-4=0,解得x=±2. (3分)
当x=±2时,y=-3.
①当x=2,y=-3时,x+2y=2+2×(-3)=-4;
②当x=-2,y=-3时,x+2y=-2+2×(-3)=-8.
∴x+2y的值是-4或-8. (6分)
21.解:(1)ab=(7-2)(7+2)=72-(2)2=49-24=25; (4分)
(2)a2+b2+3ab=(a+b)2+ab=(7-2+7+2)2+25=49+25=74. (8分)
22.解:(1)证明:在△BDC中,BC=20 cm,BD=12 cm,CD=16 cm.
∴BD2+CD2=BC2, (3分)
∴∠BDC=90°,∴△BCD是直角三角形. (4分)
(2)设AB=AC=x cm,则AD=(x-12)cm,
在Rt△ADC中,由勾股定理,得AD2+CD2=AC2,
即(x-12)2+162=x2,解得x=. (6分)
即AB=AC= cm,
∵BC=20 cm,
∴△ABC的周长是AB+AC+BC=++20=(cm). (8分)
23.解:(1)原式=(-1)+(-)+(-)+…+(-)
=-1=10-1=9; (5分)
(2)a==+1, (7分)
4a2-8a+1=4(a2-2a+1)-3=4(a-1)2-3.
当a=+1时,原式=4×()2-3=5. (10分)
24.解:(1)∵42=16>22+32,∴该三角形是钝角三角形. (2分)
(2)①若4为最长边,则42=32+x2,解得x=或x=-(舍去); (4分)
②若x为最长边,则x=32+42,得x=5,x=-5(舍去),所以x的值为5或. (6分)
(3)∵a2-b2-c2=x2+3z2-x+y2-2y+=(x-)2+(y-1)2+3z2+>0,
∴a2>b2+c2,∴该三角形是钝角三角形. (10分)
25.解:(1)如图1,PA=PB,在Rt△ACB中,AC===8. (1分)
设AP=t,则PC=8-t,
在Rt△PCB中,根据勾股定理,得(8-t)2+62=t2,解得t=,
即此时t的值为. (4分)
(2)分两种情况:
①如图2所示,点P在BC上时,过点P作PE⊥AB,
则PC=t-8,PB=14-t, (6分)
∵AP平分∠BAC,且PC⊥AC,∴PE=PC.
在△ACP与△AEP中,
,
∴△ACP≌△AEP(AAS). (7分)
∴AE=AC=8,∴BE=2. (8分)
在Rt△PEB中,根据勾股定理,得PE2+EB2=PB2,
即(t-8)2+22=(14-t)2,解得t=. (10分)
②点P又回到A点时,
∵AC+BC+AB=8+6+10=24,∴t=24.
综上所述,点P在∠BAC的平分线上时,t的值为或24. (12分)
同课章节目录
