专项训练闯关卷(三) 一次函数的应用 (含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 专项训练闯关卷(三) 一次函数的应用 (含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 105.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:25:17 | ||
图片预览


文档简介
专项训练卷(三) 一次函数的应用
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题5分,共30分)
1.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是 ( )
2.已知A,B两地相距3千米,小明从A地到B地,平均速度为4千米/时,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y关于x的函数解析式是 ( )
A.y=4x(x≥0) B.y=4x-3(x≥)
C.y=3-4x(0≤x≤) D.y=3-4x(x≥0)
3.一个装有进水管和出水管的空容器,从某时刻开始4 min内只进水不出水,容器内存水8 L;在随后的8 min内既进水又出水,容器内存水12 L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,则容器内的水量y(L)与时间x(min)之间的函数关系的图象大致的是( )
4.如果函数y=kx+b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是 ( )
A.k>0且b≤0 B.k≥0且b≤0
C.k≥0且b<0 D.k>0且b<0
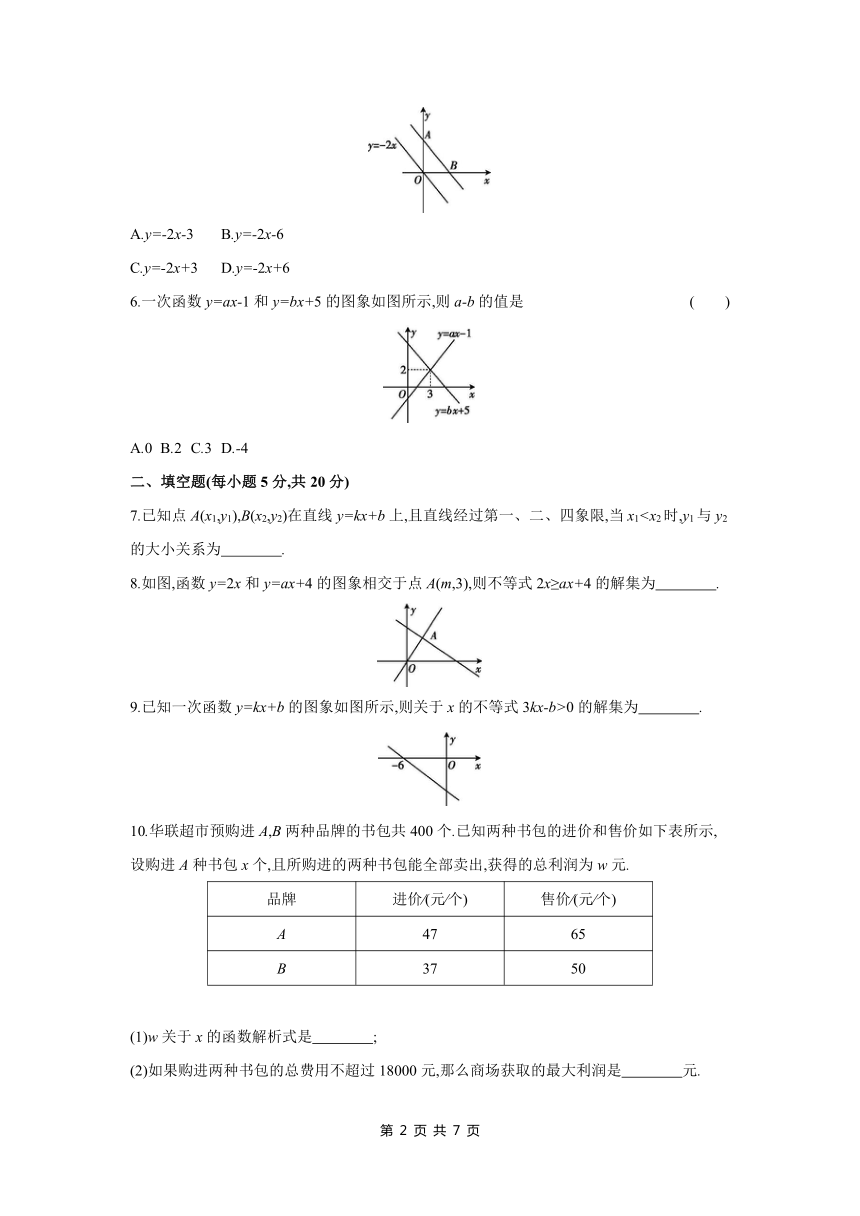
5.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=6,则直线AB的解析式是 ( )
A.y=-2x-3 B.y=-2x-6
C.y=-2x+3 D.y=-2x+6
6.一次函数y=ax-1和y=bx+5的图象如图所示,则a-b的值是 ( )
A.0 B.2 C.3 D.-4
二、填空题(每小题5分,共20分)
7.已知点A(x1,y1),B(x2,y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x18.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为 .
9.已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为 .
10.华联超市预购进A,B两种品牌的书包共400个.已知两种书包的进价和售价如下表所示,设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为w元.
品牌 进价∕(元∕个) 售价∕(元∕个)
A 47 65
B 37 50
(1)w关于x的函数解析式是 ;
(2)如果购进两种书包的总费用不超过18000元,那么商场获取的最大利润是 元.
三、解答题(本大题共4小题,共50分)
11.(10分)小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王行驶的时间x(h)之间的函数关系.
(1)小王和小李的速度分别是多少
(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.
12.(12分)为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)问:1只A型节能灯和1只B型节能灯的售价各是多少元
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
13.(14分)甲、乙两台机器共同加工一批零件,一共用了6小时,在加工过程中,乙机器因故障停止工作,排除故障后,乙机器提高工作效率,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数y(个)与甲机器加工时间x(h)之间的函数图象如图所示.
(1)这批零件一共有 个,甲机器每小时加工 个零件,乙机器排除故障后每小时加工 个零件;
(2)当3≤x≤6时,求y与x之间的函数解析式;
(3)在整个加工过程中,甲机器加工多长时间时,甲机器与乙机器加工的零件个数相等
14.(14分)某仓库有甲种货物360吨,乙种货物290吨,计划用A,B两种共50辆货车运往外地.已知一辆A种货车的运费需0.5万元,一辆B种货车的运费需0.8万元.
(1)设A种货车为x辆,运输这批货物的总运费为y万元,试写出y与x之间的函数表达式.
(2)若一辆A种货车能装载甲种货物9吨和乙种货物3吨;一辆B种货车能装载甲种货物6吨和乙种货物8吨.按此要求安排A,B两种货车运送这批货物,有哪几种运输方案 请设计出来.
(3)试说明哪种方案总运费最少,最少运费是多少万元
参考答案
一、选择题
1 2 3 4 5 6
D C A B D B
二、填空题
7 8 9 10
y1>y2 x≥ x<2 (1)w=5x+5200(0≤x≤400) (2)6800
10.(1)w=5x+5200(0≤x≤400);(2)6800 【解析】(1)由题意可知,购进B种书包为(400-x)个,则w=(65-47)x+(50-37)(400-x)=5x+5200,0≤x≤400;(2)由题意可知,47x+37(400-x)≤18000,解得x≤320,又∵w=5x+5200,5>0,w随x的增大而增大,故x=320时,w取最大值,故w最大为5×320+5200=6800(元).
三、解答题
11.解:(1)从线段AB得两人从相距30 km的两地同时出发,1 h后相遇,则v小王+v小李=30 km/h,小王从甲地到乙地行驶了3 h,∴v小王=30÷3=10(km/h),∴v小李=20 km/h. (5分)
(2)C点的意义是小李骑车从乙地到甲地用了30÷20=1.5(h),此时小王和小李的距离是1.5×10=15(km),∴点C的坐标是(1.5,15).
设直线BC的解析式为y=kx+b,将点B(1,0)、C(1.5,15)分别代入解析式,得,
解得.
∴线段BC的解析式为y=30x-30(1≤x≤1.5). (10分)
12.解:(1)设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元.
根据题意,得,解得.
答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元. (6分)
(2)设购买A型节能灯a只,则购买B型节能灯(200-a)只,总费用为w元.
w=5a+7(200-a)=-2a+1400,
∵a≤3(200-a),∴a≤150,∵-2<0,w随a的增大而减小,
∴当a=150时,w取得最小值,此时200-a=50.
答:最省钱的购买方案是购买A型节能灯150只,B型节能灯50只. (12分)
13.解:(1)270 20 40 (4分)
提示:这批零件一共有270个.
甲机器每小时加工零件(90-50)÷(3-1)=20(个).
乙机器排除故障后每小时加工零件(270-90-20×3)÷3=40(个).
(2)设当3≤x≤6时,y与x之间的函数解析式为y=kx+b,
把点B(3,90)、C(6,270)代入解析式,得,解得.
∴y=60x-90(3≤x≤6). (9分)
(3)设甲机器加工x小时时,甲机器与乙机器加工的零件个数相等.
①乙机器故障之前,每小时生产50-20=30(个),
则有20x=30,解得x=1.5;
②乙机器故障之后,有20x=30+40(x-3),解得x=4.5.
答:甲加工1.5 h或4.5 h时,甲机器与乙机器加工的零件个数相等. (14分)
14.解:(1)设A种货车为x辆,则B种货车为(50-x)辆.
根据题意,得y=0.5x+0.8(50-x),即y=-0.3x+40. (4分)
(2)根据题意,得
,
解这个不等式组,得20≤x≤22.
∵x是整数,∴x可取20,21,22.
即共有三种方案: (9分)
方案 A(辆) B(辆)
一 20 30
二 21 29
三 22 28
(3)由(1)可知,总运费y=-0.3x+40,
∵k=-0.3<0,
∴一次函数y=-0.3x+40的函数值随x的增大而减小.
∴x=22时,y有最小值,y=-0.3×22+40=33.4(万元)
选择方案三:A种货车为22辆,B种货车为28辆,总运费最少是33.4万元. (14分)
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题5分,共30分)
1.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是 ( )
2.已知A,B两地相距3千米,小明从A地到B地,平均速度为4千米/时,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y关于x的函数解析式是 ( )
A.y=4x(x≥0) B.y=4x-3(x≥)
C.y=3-4x(0≤x≤) D.y=3-4x(x≥0)
3.一个装有进水管和出水管的空容器,从某时刻开始4 min内只进水不出水,容器内存水8 L;在随后的8 min内既进水又出水,容器内存水12 L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,则容器内的水量y(L)与时间x(min)之间的函数关系的图象大致的是( )
4.如果函数y=kx+b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是 ( )
A.k>0且b≤0 B.k≥0且b≤0
C.k≥0且b<0 D.k>0且b<0
5.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=6,则直线AB的解析式是 ( )
A.y=-2x-3 B.y=-2x-6
C.y=-2x+3 D.y=-2x+6
6.一次函数y=ax-1和y=bx+5的图象如图所示,则a-b的值是 ( )
A.0 B.2 C.3 D.-4
二、填空题(每小题5分,共20分)
7.已知点A(x1,y1),B(x2,y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x1
9.已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为 .
10.华联超市预购进A,B两种品牌的书包共400个.已知两种书包的进价和售价如下表所示,设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为w元.
品牌 进价∕(元∕个) 售价∕(元∕个)
A 47 65
B 37 50
(1)w关于x的函数解析式是 ;
(2)如果购进两种书包的总费用不超过18000元,那么商场获取的最大利润是 元.
三、解答题(本大题共4小题,共50分)
11.(10分)小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王行驶的时间x(h)之间的函数关系.
(1)小王和小李的速度分别是多少
(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.
12.(12分)为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)问:1只A型节能灯和1只B型节能灯的售价各是多少元
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
13.(14分)甲、乙两台机器共同加工一批零件,一共用了6小时,在加工过程中,乙机器因故障停止工作,排除故障后,乙机器提高工作效率,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数y(个)与甲机器加工时间x(h)之间的函数图象如图所示.
(1)这批零件一共有 个,甲机器每小时加工 个零件,乙机器排除故障后每小时加工 个零件;
(2)当3≤x≤6时,求y与x之间的函数解析式;
(3)在整个加工过程中,甲机器加工多长时间时,甲机器与乙机器加工的零件个数相等
14.(14分)某仓库有甲种货物360吨,乙种货物290吨,计划用A,B两种共50辆货车运往外地.已知一辆A种货车的运费需0.5万元,一辆B种货车的运费需0.8万元.
(1)设A种货车为x辆,运输这批货物的总运费为y万元,试写出y与x之间的函数表达式.
(2)若一辆A种货车能装载甲种货物9吨和乙种货物3吨;一辆B种货车能装载甲种货物6吨和乙种货物8吨.按此要求安排A,B两种货车运送这批货物,有哪几种运输方案 请设计出来.
(3)试说明哪种方案总运费最少,最少运费是多少万元
参考答案
一、选择题
1 2 3 4 5 6
D C A B D B
二、填空题
7 8 9 10
y1>y2 x≥ x<2 (1)w=5x+5200(0≤x≤400) (2)6800
10.(1)w=5x+5200(0≤x≤400);(2)6800 【解析】(1)由题意可知,购进B种书包为(400-x)个,则w=(65-47)x+(50-37)(400-x)=5x+5200,0≤x≤400;(2)由题意可知,47x+37(400-x)≤18000,解得x≤320,又∵w=5x+5200,5>0,w随x的增大而增大,故x=320时,w取最大值,故w最大为5×320+5200=6800(元).
三、解答题
11.解:(1)从线段AB得两人从相距30 km的两地同时出发,1 h后相遇,则v小王+v小李=30 km/h,小王从甲地到乙地行驶了3 h,∴v小王=30÷3=10(km/h),∴v小李=20 km/h. (5分)
(2)C点的意义是小李骑车从乙地到甲地用了30÷20=1.5(h),此时小王和小李的距离是1.5×10=15(km),∴点C的坐标是(1.5,15).
设直线BC的解析式为y=kx+b,将点B(1,0)、C(1.5,15)分别代入解析式,得,
解得.
∴线段BC的解析式为y=30x-30(1≤x≤1.5). (10分)
12.解:(1)设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元.
根据题意,得,解得.
答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元. (6分)
(2)设购买A型节能灯a只,则购买B型节能灯(200-a)只,总费用为w元.
w=5a+7(200-a)=-2a+1400,
∵a≤3(200-a),∴a≤150,∵-2<0,w随a的增大而减小,
∴当a=150时,w取得最小值,此时200-a=50.
答:最省钱的购买方案是购买A型节能灯150只,B型节能灯50只. (12分)
13.解:(1)270 20 40 (4分)
提示:这批零件一共有270个.
甲机器每小时加工零件(90-50)÷(3-1)=20(个).
乙机器排除故障后每小时加工零件(270-90-20×3)÷3=40(个).
(2)设当3≤x≤6时,y与x之间的函数解析式为y=kx+b,
把点B(3,90)、C(6,270)代入解析式,得,解得.
∴y=60x-90(3≤x≤6). (9分)
(3)设甲机器加工x小时时,甲机器与乙机器加工的零件个数相等.
①乙机器故障之前,每小时生产50-20=30(个),
则有20x=30,解得x=1.5;
②乙机器故障之后,有20x=30+40(x-3),解得x=4.5.
答:甲加工1.5 h或4.5 h时,甲机器与乙机器加工的零件个数相等. (14分)
14.解:(1)设A种货车为x辆,则B种货车为(50-x)辆.
根据题意,得y=0.5x+0.8(50-x),即y=-0.3x+40. (4分)
(2)根据题意,得
,
解这个不等式组,得20≤x≤22.
∵x是整数,∴x可取20,21,22.
即共有三种方案: (9分)
方案 A(辆) B(辆)
一 20 30
二 21 29
三 22 28
(3)由(1)可知,总运费y=-0.3x+40,
∵k=-0.3<0,
∴一次函数y=-0.3x+40的函数值随x的增大而减小.
∴x=22时,y有最小值,y=-0.3×22+40=33.4(万元)
选择方案三:A种货车为22辆,B种货车为28辆,总运费最少是33.4万元. (14分)
