第三章 图形的平移与旋转 基础闯关卷(含答案) 2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 第三章 图形的平移与旋转 基础闯关卷(含答案) 2024-2025学年北师大版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 333.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:38:45 | ||
图片预览


文档简介
第三章 图形的平移与旋转
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
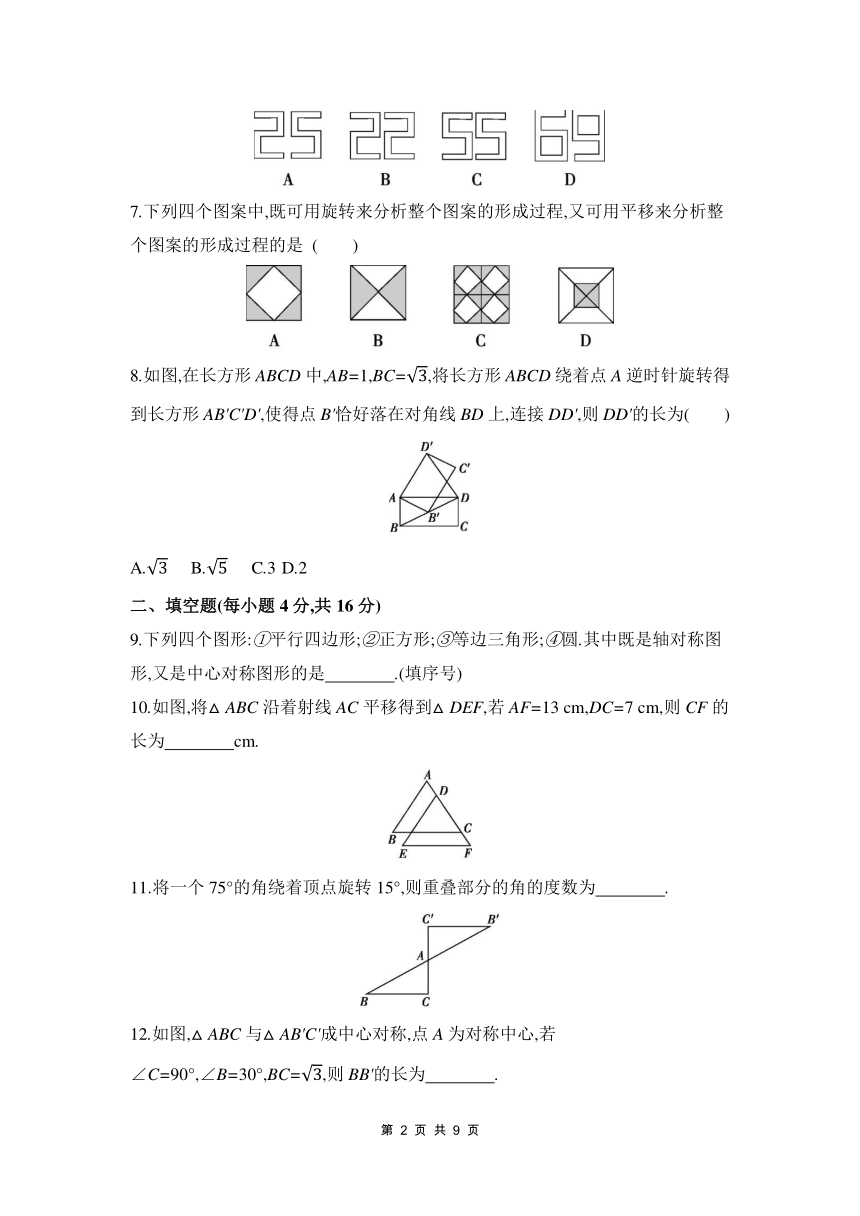
1.下列选项中的各图形是由左边的图形平移得到的是 ( )
2.如图,将“新月形”图案绕着它的中心顺时针旋转90°后,可以得到的图案是( )
3.在平面直角坐标系中,点P(-2,1)关于原点成中心对称的点的坐标为 ( )
A.(2,1) B.(-2,-1) C.(-2,1) D.(2,-1)
4.如图,在平面直角坐标系中,将点A先向左平移2个单位长度,再向下平移3个单位长度得到点B,则点B的坐标为 ( )
A.(-4,0) B.(-4,6) C.(-2,0) D.(-3,0)
5.小明设计的图案如图所示,该图案绕着旋转中心旋转一定角度后能够与自身重合,则这个旋转角度可以是 ( )
A.45° B.72° C.90° D.120°
6.下列四组图形中,左边的图形与右边的图形不成中心对称的是 ( )
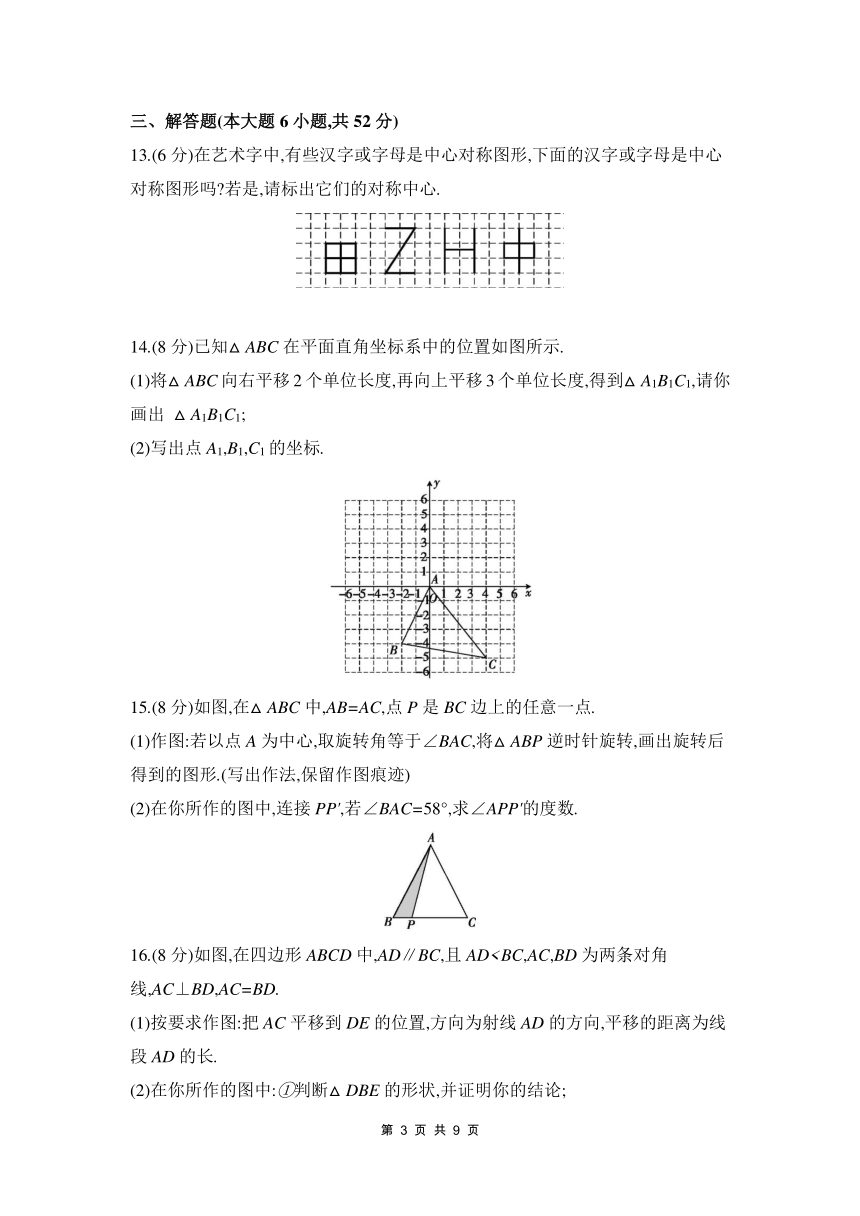
7.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的是 ( )
8.如图,在长方形ABCD中,AB=1,BC=,将长方形ABCD绕着点A逆时针旋转得到长方形AB'C'D',使得点B'恰好落在对角线BD上,连接DD',则DD'的长为( )
A. B. C.3 D.2
二、填空题(每小题4分,共16分)
9.下列四个图形:①平行四边形;②正方形;③等边三角形;④圆.其中既是轴对称图形,又是中心对称图形的是 .(填序号)
10.如图,将△ABC沿着射线AC平移得到△DEF,若AF=13 cm,DC=7 cm,则CF的长为 cm.
将一个75°的角绕着顶点旋转15°,则重叠部分的角的度数为 .
12.如图,△ABC与△AB'C'成中心对称,点A为对称中心,若∠C=90°,∠B=30°,BC=,则BB'的长为 .
三、解答题(本大题6小题,共52分)
13.(6分)在艺术字中,有些汉字或字母是中心对称图形,下面的汉字或字母是中心对称图形吗 若是,请标出它们的对称中心.
14.(8分)已知△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移2个单位长度,再向上平移3个单位长度,得到△A1B1C1,请你画出 △A1B1C1;
(2)写出点A1,B1,C1的坐标.
15.(8分)如图,在△ABC中,AB=AC,点P是BC边上的任意一点.
(1)作图:若以点A为中心,取旋转角等于∠BAC,将△ABP逆时针旋转,画出旋转后得到的图形.(写出作法,保留作图痕迹)
(2)在你所作的图中,连接PP',若∠BAC=58°,求∠APP'的度数.
16.(8分)如图,在四边形ABCD中,AD∥BC,且AD(1)按要求作图:把AC平移到DE的位置,方向为射线AD的方向,平移的距离为线段AD的长.
(2)在你所作的图中:①判断△DBE的形状,并证明你的结论;
②若AC=3 cm,求BE的长.
17.(10分)如图,在Rt△ABC中,∠C=90°,把Rt△ABC绕着点B逆时针旋转,得到Rt△DBE,点E在AB上.
(1)若∠BDA=70°,求∠BAC的度数;
(2)若BC=8,AC=6,求△ABD中AD边上的高.
18.(12分)问题情境:如图1,在正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
画图探究:(1)画出△ABC绕着点A按逆时针方向旋转90°后得到的△AB1C1(不写画法).若连接CC1,则△ACC1是什么三角形 请说明理由.
(2)画出△A2B2C2,使△A2B2C2和△AB1C1关于点O成中心对称.
继续探究:(3)写出如何平移△AB1C1,使得△A2B2C2和△AB1C1能拼成一个长方形.
深入探究:(4)小明利用图1中的Rt△ABC设计了如图2所示的图案,你能分析这个图案的形成过程吗 试试看.
(5)请你利用图1中的Rt△ABC若干个或Rt△ABC若干个及圆各设计一个图案,使整个图案为旋转对称图形或中心对称图形.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C C D A B A C A
1.C 【解析】根据平移的概念可知,选项C的图形是由左边的图形平移得到的,其他均不是.
2.C 【解析】由图可知,将“新月形”图案绕着它的中心顺时针旋转90°后,得到的图案为选项C.
3.D 【解析】关于原点成中心对称的点的坐标特征是横、纵坐标都互为相反数.
4.A 【解析】由图可知,点A的坐标为(-2,3),∴将点A先向左平移2个单位长度,再向下平移3个单位长度得到的点B的坐标为(-4,0).
5.B 【解析】由图可知,这个旋转角度可以是360°÷5=72°或72°的整数倍.
6.A 【解析】由图可知,左边的图形与右边的图形成中心对称的是B,C,D选项,只有A选项不是.
7.C 【解析】A,B,C,D四个选项中的图形都可以看成是图形的一半旋转180°得到.若一个图形可以通过某一个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线应该是平行的,∴A,B,D不能由平移得到,只有C选项的图形,可以看成是由基本图形通过平移得到的.
8.A 【解析】在长方形ABCD中,AB=1,BC=,∴AD=BC=,∴BD=2,∴∠ADB=30°,∴∠ABD=60°,∵AB=AB',∴△ABB'是等边三角形,∴∠BAB'=60°,∴∠DAD'=60°,∴△ADD'是等边三角形,∴DD'=AD=BC=.
二、填空题
9.②④ 【解析】①只是中心对称图形;②④既是轴对称图形,又是中心对称图形的是;③只是轴对称图形.
10.3 【解析】根据平移的性质可得AD=CF,∵AF=AD+DC+CF,∴13=2CF+7,∴CF=3 cm.
解题思路 根据平移的性质得出AD=CF,再利用AF=13,DC=7,即可求出CF的长.
命题分析 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行(或共线)且相等.
【拓展设问】如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置.已知点A,D之间的距离为1,CE=2,则BF的长为 .
【答案】4 ∵将三角形ABC沿水平方向向右平移到三角形DEF的位置,∴BE=CF=AD=1,∴BF=BE+CE+CF=1+2+1=4.
11.60° 【解析】如图所示,根据题意画出图形.∵∠AOB=75°,∠BOD=15°,∴∠AOD=∠AOB-∠BOD=75°-15°=60°.
12.4 【解析】设AC=x,∵∠B=30°,∴AB=2x,在Rt△ABC中,根据勾股定理,得(2x)2=x2+()2,即x2=1,解得x=1(负值舍去),∴AB=2,∴BB'=4.
三、解答题
13.解:“田”“Z”“H”“中”都是中心对称图形. (3分)
它们的对称中心如下图: (6分)
14.解:(1)如图,△A1B1C1为所求. (5分)
(2)A1(2,3),B1(0,-1),C1(6,-2). (8分)
15.解:(1)如图,△ACP'为所求. (2分)
作法:①作∠PAD=∠BAC;
②在射线AD上截取AP'=AP;
③连接CP',则△ACP'就是所作的三角形. (4分)
(2)∵∠BAC=∠PAP',∠BAC=58°,∴∠PAP'=58°,
∵AP=AP',∴∠APP'=∠AP'P, (6分)
∴∠APP'=(180°-∠PAP')=×(180°-58°)=61°. (8分)
16.解:(1)如图,线段DE为所求. (3分)
(2)①△DBE是等腰直角三角形. (4分)
证明:由平移的性质可得,DE=AC,DE∥AC,
∵AC⊥BD,∴DE⊥BD,
∵AC=BD,∴DE=BD,
∴△DBE是等腰直角三角形. (6分)
②∵AC=3,∴DE=AC=BD=3,
∵∠BDE=90°,
∴BE===3. (8分)
17.解:(1)由旋转性质知BD=BA,∠CBA=∠EBD,
∵∠BDA=70°,∴∠BAD=70°,∴∠ABD=∠ABC=40°,
∵∠C=90°,∴∠BAC=50°. (4分)
(2)如图,过点B作BF⊥AD于点F.
∵BC=8,AC=6,∠C=90°,∴AB=10,
由旋转的性质知△ABC≌△DBE,则BE=BC=8,DE=AC=6,∴AE=2,
在Rt△ADE中,AD===2, (7分)
∵BA=BD,∴AF=AD=,
∴BF===3. (10分)
解题思路 (1)由旋转的性质和等腰三角形的性质即可得到结论;(2)由旋转的性质得BE=BC=8,DE=AC=6,AB=BD=10,从而得AE=2,利用勾股定理得AD=2,作BF⊥AD得AF=AD=,再次利用勾股定理可得答案.
【拓展设问】如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,则BM的长是 .
【答案】1+ 如图,连接AM,在Rt△ABC中,AC===2.由题意及旋转的性质,得CA=CM=2,∠ACM=60°,∴△ACM是等边三角形,∴CM=AM=2.∵AB=BC,CM=AM,∴BM垂直平分AC,∴AO=AC=1.在等腰Rt△ABC中,∠BAC=45°,∴∠BAC=∠OBA=45°,∴AO=BO=1.在Rt△AOM中,OM===.∴BM=OB+OM=1+.
高分技巧 一些图形经过旋转,旋转前后对应边相等,这样就会形成新的等腰或等边三角形,解题时要注意发挥这些隐蔽的特殊三角形的解题功能.
18.解:(1)如图,△AB1C1为所求. (2分)
△ACC1是等腰直角三角形.
理由:由旋转的性质得,AC=AC1,∠CAC1=90°,
∴△ACC1是等腰直角三角形. (4分)
(2)如图,△A2B2C2为所求. (6分)
(3)由图可知,将△AB1C1向右平移5个单位长度,再向下平移6个单位长度,与△A2B2C2能拼成一个长方形. (8分)
(4)以其中一个直角三角形为基本图案,按顺时针方向连续旋转7次,每次旋转的角度为45°得到该图案. (10分)
(5)设计的图案如下图. (12分)
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列选项中的各图形是由左边的图形平移得到的是 ( )
2.如图,将“新月形”图案绕着它的中心顺时针旋转90°后,可以得到的图案是( )
3.在平面直角坐标系中,点P(-2,1)关于原点成中心对称的点的坐标为 ( )
A.(2,1) B.(-2,-1) C.(-2,1) D.(2,-1)
4.如图,在平面直角坐标系中,将点A先向左平移2个单位长度,再向下平移3个单位长度得到点B,则点B的坐标为 ( )
A.(-4,0) B.(-4,6) C.(-2,0) D.(-3,0)
5.小明设计的图案如图所示,该图案绕着旋转中心旋转一定角度后能够与自身重合,则这个旋转角度可以是 ( )
A.45° B.72° C.90° D.120°
6.下列四组图形中,左边的图形与右边的图形不成中心对称的是 ( )
7.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的是 ( )
8.如图,在长方形ABCD中,AB=1,BC=,将长方形ABCD绕着点A逆时针旋转得到长方形AB'C'D',使得点B'恰好落在对角线BD上,连接DD',则DD'的长为( )
A. B. C.3 D.2
二、填空题(每小题4分,共16分)
9.下列四个图形:①平行四边形;②正方形;③等边三角形;④圆.其中既是轴对称图形,又是中心对称图形的是 .(填序号)
10.如图,将△ABC沿着射线AC平移得到△DEF,若AF=13 cm,DC=7 cm,则CF的长为 cm.
将一个75°的角绕着顶点旋转15°,则重叠部分的角的度数为 .
12.如图,△ABC与△AB'C'成中心对称,点A为对称中心,若∠C=90°,∠B=30°,BC=,则BB'的长为 .
三、解答题(本大题6小题,共52分)
13.(6分)在艺术字中,有些汉字或字母是中心对称图形,下面的汉字或字母是中心对称图形吗 若是,请标出它们的对称中心.
14.(8分)已知△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移2个单位长度,再向上平移3个单位长度,得到△A1B1C1,请你画出 △A1B1C1;
(2)写出点A1,B1,C1的坐标.
15.(8分)如图,在△ABC中,AB=AC,点P是BC边上的任意一点.
(1)作图:若以点A为中心,取旋转角等于∠BAC,将△ABP逆时针旋转,画出旋转后得到的图形.(写出作法,保留作图痕迹)
(2)在你所作的图中,连接PP',若∠BAC=58°,求∠APP'的度数.
16.(8分)如图,在四边形ABCD中,AD∥BC,且AD
(2)在你所作的图中:①判断△DBE的形状,并证明你的结论;
②若AC=3 cm,求BE的长.
17.(10分)如图,在Rt△ABC中,∠C=90°,把Rt△ABC绕着点B逆时针旋转,得到Rt△DBE,点E在AB上.
(1)若∠BDA=70°,求∠BAC的度数;
(2)若BC=8,AC=6,求△ABD中AD边上的高.
18.(12分)问题情境:如图1,在正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
画图探究:(1)画出△ABC绕着点A按逆时针方向旋转90°后得到的△AB1C1(不写画法).若连接CC1,则△ACC1是什么三角形 请说明理由.
(2)画出△A2B2C2,使△A2B2C2和△AB1C1关于点O成中心对称.
继续探究:(3)写出如何平移△AB1C1,使得△A2B2C2和△AB1C1能拼成一个长方形.
深入探究:(4)小明利用图1中的Rt△ABC设计了如图2所示的图案,你能分析这个图案的形成过程吗 试试看.
(5)请你利用图1中的Rt△ABC若干个或Rt△ABC若干个及圆各设计一个图案,使整个图案为旋转对称图形或中心对称图形.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C C D A B A C A
1.C 【解析】根据平移的概念可知,选项C的图形是由左边的图形平移得到的,其他均不是.
2.C 【解析】由图可知,将“新月形”图案绕着它的中心顺时针旋转90°后,得到的图案为选项C.
3.D 【解析】关于原点成中心对称的点的坐标特征是横、纵坐标都互为相反数.
4.A 【解析】由图可知,点A的坐标为(-2,3),∴将点A先向左平移2个单位长度,再向下平移3个单位长度得到的点B的坐标为(-4,0).
5.B 【解析】由图可知,这个旋转角度可以是360°÷5=72°或72°的整数倍.
6.A 【解析】由图可知,左边的图形与右边的图形成中心对称的是B,C,D选项,只有A选项不是.
7.C 【解析】A,B,C,D四个选项中的图形都可以看成是图形的一半旋转180°得到.若一个图形可以通过某一个基本图形平移得到,则这个图形可以分成几个相同的基本图形,且基本图形之间对应点的连线应该是平行的,∴A,B,D不能由平移得到,只有C选项的图形,可以看成是由基本图形通过平移得到的.
8.A 【解析】在长方形ABCD中,AB=1,BC=,∴AD=BC=,∴BD=2,∴∠ADB=30°,∴∠ABD=60°,∵AB=AB',∴△ABB'是等边三角形,∴∠BAB'=60°,∴∠DAD'=60°,∴△ADD'是等边三角形,∴DD'=AD=BC=.
二、填空题
9.②④ 【解析】①只是中心对称图形;②④既是轴对称图形,又是中心对称图形的是;③只是轴对称图形.
10.3 【解析】根据平移的性质可得AD=CF,∵AF=AD+DC+CF,∴13=2CF+7,∴CF=3 cm.
解题思路 根据平移的性质得出AD=CF,再利用AF=13,DC=7,即可求出CF的长.
命题分析 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行(或共线)且相等.
【拓展设问】如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置.已知点A,D之间的距离为1,CE=2,则BF的长为 .
【答案】4 ∵将三角形ABC沿水平方向向右平移到三角形DEF的位置,∴BE=CF=AD=1,∴BF=BE+CE+CF=1+2+1=4.
11.60° 【解析】如图所示,根据题意画出图形.∵∠AOB=75°,∠BOD=15°,∴∠AOD=∠AOB-∠BOD=75°-15°=60°.
12.4 【解析】设AC=x,∵∠B=30°,∴AB=2x,在Rt△ABC中,根据勾股定理,得(2x)2=x2+()2,即x2=1,解得x=1(负值舍去),∴AB=2,∴BB'=4.
三、解答题
13.解:“田”“Z”“H”“中”都是中心对称图形. (3分)
它们的对称中心如下图: (6分)
14.解:(1)如图,△A1B1C1为所求. (5分)
(2)A1(2,3),B1(0,-1),C1(6,-2). (8分)
15.解:(1)如图,△ACP'为所求. (2分)
作法:①作∠PAD=∠BAC;
②在射线AD上截取AP'=AP;
③连接CP',则△ACP'就是所作的三角形. (4分)
(2)∵∠BAC=∠PAP',∠BAC=58°,∴∠PAP'=58°,
∵AP=AP',∴∠APP'=∠AP'P, (6分)
∴∠APP'=(180°-∠PAP')=×(180°-58°)=61°. (8分)
16.解:(1)如图,线段DE为所求. (3分)
(2)①△DBE是等腰直角三角形. (4分)
证明:由平移的性质可得,DE=AC,DE∥AC,
∵AC⊥BD,∴DE⊥BD,
∵AC=BD,∴DE=BD,
∴△DBE是等腰直角三角形. (6分)
②∵AC=3,∴DE=AC=BD=3,
∵∠BDE=90°,
∴BE===3. (8分)
17.解:(1)由旋转性质知BD=BA,∠CBA=∠EBD,
∵∠BDA=70°,∴∠BAD=70°,∴∠ABD=∠ABC=40°,
∵∠C=90°,∴∠BAC=50°. (4分)
(2)如图,过点B作BF⊥AD于点F.
∵BC=8,AC=6,∠C=90°,∴AB=10,
由旋转的性质知△ABC≌△DBE,则BE=BC=8,DE=AC=6,∴AE=2,
在Rt△ADE中,AD===2, (7分)
∵BA=BD,∴AF=AD=,
∴BF===3. (10分)
解题思路 (1)由旋转的性质和等腰三角形的性质即可得到结论;(2)由旋转的性质得BE=BC=8,DE=AC=6,AB=BD=10,从而得AE=2,利用勾股定理得AD=2,作BF⊥AD得AF=AD=,再次利用勾股定理可得答案.
【拓展设问】如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,则BM的长是 .
【答案】1+ 如图,连接AM,在Rt△ABC中,AC===2.由题意及旋转的性质,得CA=CM=2,∠ACM=60°,∴△ACM是等边三角形,∴CM=AM=2.∵AB=BC,CM=AM,∴BM垂直平分AC,∴AO=AC=1.在等腰Rt△ABC中,∠BAC=45°,∴∠BAC=∠OBA=45°,∴AO=BO=1.在Rt△AOM中,OM===.∴BM=OB+OM=1+.
高分技巧 一些图形经过旋转,旋转前后对应边相等,这样就会形成新的等腰或等边三角形,解题时要注意发挥这些隐蔽的特殊三角形的解题功能.
18.解:(1)如图,△AB1C1为所求. (2分)
△ACC1是等腰直角三角形.
理由:由旋转的性质得,AC=AC1,∠CAC1=90°,
∴△ACC1是等腰直角三角形. (4分)
(2)如图,△A2B2C2为所求. (6分)
(3)由图可知,将△AB1C1向右平移5个单位长度,再向下平移6个单位长度,与△A2B2C2能拼成一个长方形. (8分)
(4)以其中一个直角三角形为基本图案,按顺时针方向连续旋转7次,每次旋转的角度为45°得到该图案. (10分)
(5)设计的图案如下图. (12分)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
