第三章 图形的平移与旋转 能力提优卷(含答案) 2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 第三章 图形的平移与旋转 能力提优卷(含答案) 2024-2025学年北师大版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 295.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:38:58 | ||
图片预览


文档简介
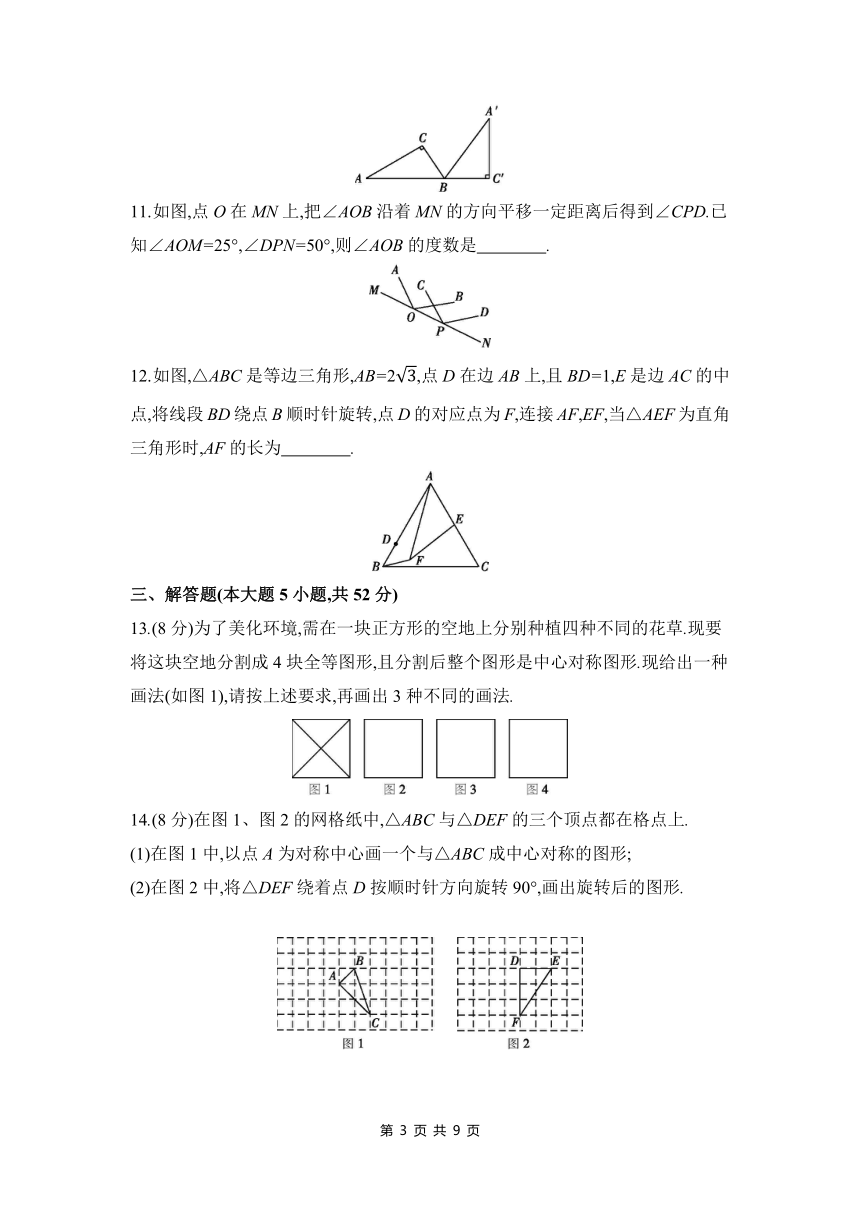
第三章 图形的平移与旋转
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列是各届冬季奥林匹克运动会会徽中的图案,其中是中心对称图形的是 ( )
A. B. C. D.
2.在下列四个图案中,能用平移变换来分析其形成过程的是 ( )
A. B. C. D.
3.如图,在△ABC中,∠A=32°,∠B=50°,将BC边绕点C逆时针旋转一周回到原来位置.在旋转过程中,当CB'∥AB时,求BC边旋转的角度.嘉嘉求出的答案是50°,琪琪求出的答案是230°,则下列说法正确的是 ( )
A.嘉嘉的结果正确
B.琪琪的结果正确
C.两个人的结果合在一起才正确
D.两个人的结果合在一起也不正确
4.在平面直角坐标系中,将点A先向下平移2个单位长度,再向右平移3个单位长度得到点A',点A'恰好与原点重合,则点A的坐标为 ( )
A.(-3,-2) B.(-3,2) C.(3,2) D.(3,-2)
5.如图,将△OAB绕点O逆时针旋转80°得到△OCD,若∠AOB=35°,则∠AOD的度数为 ( )
A.35° B.40° C.45° D.55°
6.如图,将直角△ABC沿BC方向平移得到直角△DEF,若AB=12 cm,BE=5 cm,DH=4 cm,则图中阴影部分的面积为 ( )
A.40 cm2 B.48 cm2 C.50 cm2 D.60 cm2
7.如图,将一块含30°角的直角三角板放置在平行线a,b之间,且较长直角边靠在直线a上,然后将三角板绕着顶点A逆时针旋转25°后另一个顶点B恰好落在直线b上,这时直角边BC与直线b所构成的∠1的度数为 ( )
A.70° B.65° C.60° D.55°
8.如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将△APC绕着点A逆时针旋转60°得到△AEF,则AE+PB+PC的最小值为 ( )
A.2 B.8 C.5 D.6
二、填空题(每小题4分,共16分)
9.在平面直角坐标系中,将点(2,1)向下平移3个单位长度后得到的点的坐标是 .
10.如图,将直角△ABC(其中∠ABC=60°)绕点B顺时针旋转一个角度到△A'BC'的位置,使得点A,B,C'在同一条直线上,则这个旋转的角度为 .
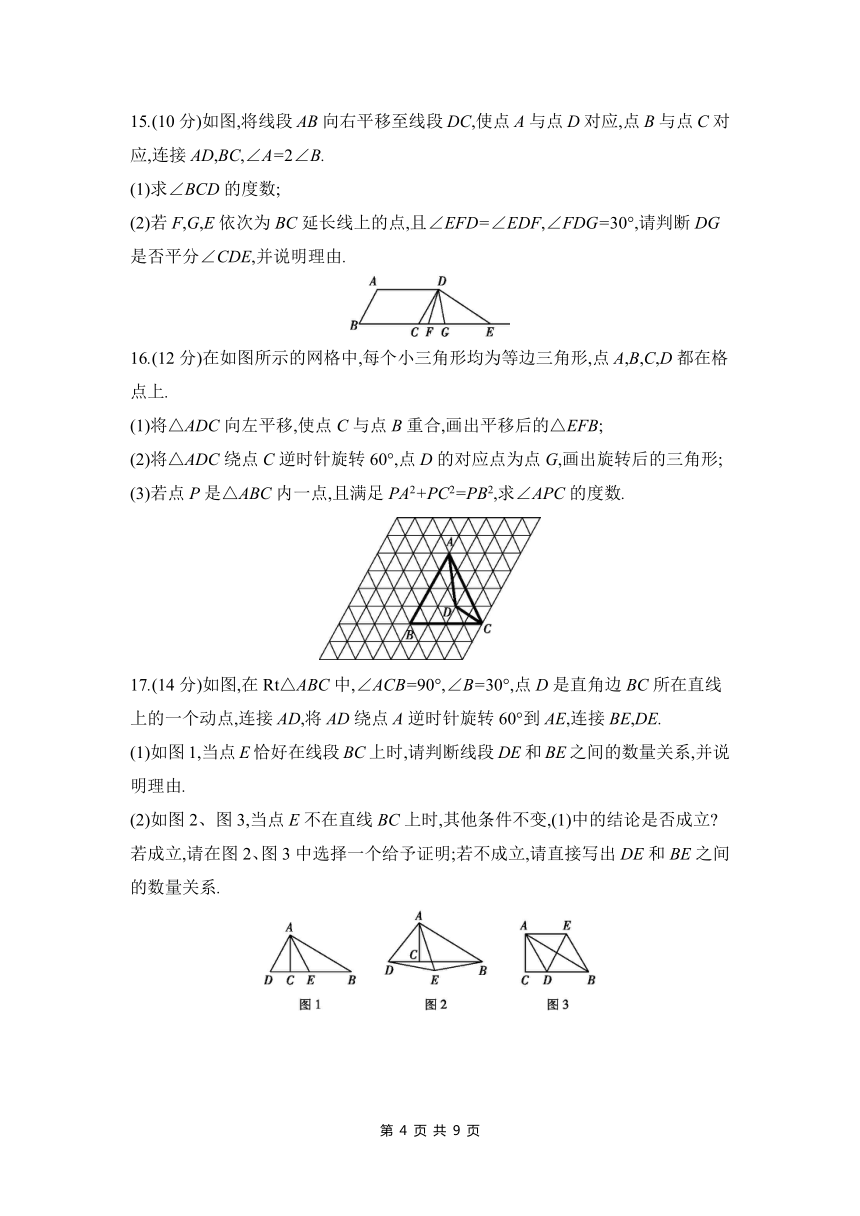
如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得到∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的度数是 .
如图,△ABC是等边三角形,AB=2,点D在边AB上,且BD=1,E是边AC的中点,将线段BD绕点B顺时针旋转,点D的对应点为F,连接AF,EF,当△AEF为直角三角形时,AF的长为 .
三、解答题(本大题5小题,共52分)
13.(8分)为了美化环境,需在一块正方形的空地上分别种植四种不同的花草.现要将这块空地分割成4块全等图形,且分割后整个图形是中心对称图形.现给出一种画法(如图1),请按上述要求,再画出3种不同的画法.
14.(8分)在图1、图2的网格纸中,△ABC与△DEF的三个顶点都在格点上.
(1)在图1中,以点A为对称中心画一个与△ABC成中心对称的图形;
(2)在图2中,将△DEF绕着点D按顺时针方向旋转90°,画出旋转后的图形.
15.(10分)如图,将线段AB向右平移至线段DC,使点A与点D对应,点B与点C对应,连接AD,BC,∠A=2∠B.
(1)求∠BCD的度数;
(2)若F,G,E依次为BC延长线上的点,且∠EFD=∠EDF,∠FDG=30°,请判断DG是否平分∠CDE,并说明理由.
16.(12分)在如图所示的网格中,每个小三角形均为等边三角形,点A,B,C,D都在格点上.
(1)将△ADC向左平移,使点C与点B重合,画出平移后的△EFB;
(2)将△ADC绕点C逆时针旋转60°,点D的对应点为点G,画出旋转后的三角形;
(3)若点P是△ABC内一点,且满足PA2+PC2=PB2,求∠APC的度数.
17.(14分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,点D是直角边BC所在直线上的一个动点,连接AD,将AD绕点A逆时针旋转60°到AE,连接BE,DE.
(1)如图1,当点E恰好在线段BC上时,请判断线段DE和BE之间的数量关系,并说明理由.
(2)如图2、图3,当点E不在直线BC上时,其他条件不变,(1)中的结论是否成立 若成立,请在图2、图3中选择一个给予证明;若不成立,请直接写出DE和BE之间的数量关系.
参考答案
一、选择题
1 2 3 4 5 6 7 8
A B C B C C B A
3.C 【解析】在△ABC中,∠A=32°,∠B=50°,∴∠ACB=180°-32°-50°=98°,如图,当CB'∥AB时,旋转角=∠B=50°,当CB″∥AB时,∠B″CA=∠A=32°,∴旋转角=360°-32°-98°=230°,综上所述,两个人的结果合在一起才正确.
4.B 【解析】∵点A先向下平移2个单位长度,再向右平移3个单位长度得到点A',点A'恰好与原点重合,∴原点(0,0)先向左平移3个单位长度,再向上平移2个单位长度,得到点A(-3,2).
解题思路 利用平移的性质解决问题即可.
答题妙招 点的平移变换与坐标的变化规律:点(x,y)右(左)平移m个单位长度,得对应点的坐标为(x±m,y),点(x,y)上(下)平移n个单位长度,得对应点的坐标为(x,y±n).根据这些平移规律可以解决很多中考中与坐标系平移有关的问题.
5.C 【解析】∵△OAB绕点O逆时针旋转80°得到△OCD,∴∠BOD=80°,∴∠AOD=∠BOD-∠AOB=80°-35°=45°.
6.C 【解析】∵Rt△ABC沿BC方向平移得到Rt△DEF,∴AB=DE=12 cm,△ABC≌△DEF,∴阴影部分面积=梯形ABEH的面积,∵DH=4 cm,∴EH=12-4=8(cm),∴阴影部分的面积=×(8+12)×5=50(cm2).
7.B 【解析】如图,根据题意,得∠3=∠BAC+25°=25°+30°=55°,∵a∥b,∴∠2=∠3=55°,∵∠1+∠2+∠ABC=180°,∴∠1=180°-55°-60°=65°.
8.A 【解析】如图,连接PE,BF,过点B作AF的垂线交FA的延长线于G,∵△APC绕着点A逆时针旋转60°得到△AEF,∴AP=AE,∠PAE=∠CAF=60°,PC=EF,∴△APE为等边三角形,即AE=PE,∴AE+PB+PC=PB+PE+EF≥BF,∵∠BAC=60°,∴∠BAF=120°,∴∠BAG=60°,∴AG=AB=2,GF=2+6=8,∴BG===2,∴BF===2.
二、填空题
9.(2,-2) 【解析】将点(2,1)向下平移3个单位长度所得点的坐标为(2,1-3),即(2,-2).
10.120° 【解析】由题意可知∠A'BC'=∠ABC=60°,∴这个旋转的角度是∠ABA'=180°-∠A'BC'=180°-60°=120°.
11.105° 【解析】∵∠AOB沿着MN的方向平移一定距离后得到∠CPD,∴BO∥DP,∴∠BON=∠DPN=50°,∴∠AOB=180°-25°-50°=105°.
12.或 【解析】∵△ABC是等边三角形,E是边AC的中点,∴只能是∠AEF=90°,当点F在△ABC内时,∠AEF=90°,此时,点B,F,E三点共线,且点F在点B,E之间,∴BE===3,∴EF=BE-BF=3-1=2,∴AF===;当点F在△ABC外时,∠AEF=90°,此时,点B,F,E三点共线,且点B在点F,E之间,此时,EF=BE+BF=3+1=4,∴AF===.
解题思路 根据题意,判断出只能是∠AEF=90°,分两种情形,点B,F,E三点共线,且点F在点B,E之间,或点B,F,E三点共线,且点B在点F,E之间,分别通过勾股定理求AF的长即可.
易错警示 由于缺乏分类意识而忽略“点B,F,E三点共线,且点B在点F,E之间”的情形,而导致丢值掉解.
【拓展设问】一副三角板按如图所示的方式放置,将三角板ADE绕点A逆时针旋转α(0°<α<90°),使得三角板ADE的一边所在的直线与BC垂直,则α的度数为 .
【答案】15°或60° 分两种情形讨论:当DE⊥BC时,∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;当AD⊥BC时,α=90°-∠C=90°-30°=60°.故α的度数为15°或60°.
答题妙招 解与旋转有关的问题时,由于旋转方向、旋转角度或图形的位置与形状等不确定因素的影响而引发分类讨论,从而造成答案不唯一.
三、解答题
13.解:如图所示. (8分)
14.解:(1)如图1,△AB'C'为所求; (4分)
(2)如图2,△DE'F'为所求. (8分)
15.解:(1)由平移特征,可得AB∥DC,AD∥BC,
∴∠B+∠BCD=180°,∠A+∠B=180°.
∵∠A=2∠B,∴∠B=60°,
∴∠BCD=180°-60°=120°. (4分)
(2)DG平分∠CDE. (5分)
理由:∵AB∥CD,∴∠DCE=∠B=60°.
由三角形的外角性质,得∠CDF=∠DFE-60°,
又∵∠FDG=30°,∴∠CDG=∠CDF+30°=∠DFE-60°+30°=∠DFE-30°.
∵∠EDG=∠EDF-∠FDG=∠EDF-30°,
又∵∠DFE=∠EDF,
∴∠CDG=∠EDG,
∴DG平分∠CDE. (10分)
16.解:(1)如图所示,△EFB为所求; (3分)
(2)如图所示,△BCG为所求; (6分)
(3)如图所示,将△ABP绕点A逆时针旋转60°得到△ACD,连接PD,∴△ADP是等边三角形,CD=BP,∴∠APD=60°,AP=DP,∵PA2+PC2=PB2,∴PD2+PC2=CD2,∴△CPD是直角三角形,∴∠CPD=90°,∴∠APC=∠APD+∠CPD=60°+90°=150°. (12分)
17.解:(1)DE=BE. (1分)
理由:由旋转可知,AD=AE,∠DAE=60°,
∴△ADE为等边三角形,∴DE=AE,∠AED=60°.
∵∠ABC=30°,∠AED=∠ABC+∠EAB,∴∠EAB=60°-30°=30°,∴∠ABC=∠EAB,∴BE=AE,∴DE=BE. (6分)
(2)图2、图3中结论仍成立. (7分)
选择图2证明:如图,过点E作EF⊥AB,垂足为点F.
在Rt△ABC中,∠ACB=90°,∠ABC=30°,
∴∠CAB=60°,∴∠DAE=∠CAB,
∴∠DAE-∠CAE=∠CAB-∠CAE,即∠CAD=∠EAF,又∵AD=AE,∠ACD=∠AFE=90°,∴△ADC≌△AEF(AAS),∴AC=AF.
∵在Rt△ABC中,∠ABC=30°,∴AC=AB,∴AF=AB.
又∵EF⊥AB,∴AE=BE.
由(1)知AE=DE,∴DE=BE. (14分)
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列是各届冬季奥林匹克运动会会徽中的图案,其中是中心对称图形的是 ( )
A. B. C. D.
2.在下列四个图案中,能用平移变换来分析其形成过程的是 ( )
A. B. C. D.
3.如图,在△ABC中,∠A=32°,∠B=50°,将BC边绕点C逆时针旋转一周回到原来位置.在旋转过程中,当CB'∥AB时,求BC边旋转的角度.嘉嘉求出的答案是50°,琪琪求出的答案是230°,则下列说法正确的是 ( )
A.嘉嘉的结果正确
B.琪琪的结果正确
C.两个人的结果合在一起才正确
D.两个人的结果合在一起也不正确
4.在平面直角坐标系中,将点A先向下平移2个单位长度,再向右平移3个单位长度得到点A',点A'恰好与原点重合,则点A的坐标为 ( )
A.(-3,-2) B.(-3,2) C.(3,2) D.(3,-2)
5.如图,将△OAB绕点O逆时针旋转80°得到△OCD,若∠AOB=35°,则∠AOD的度数为 ( )
A.35° B.40° C.45° D.55°
6.如图,将直角△ABC沿BC方向平移得到直角△DEF,若AB=12 cm,BE=5 cm,DH=4 cm,则图中阴影部分的面积为 ( )
A.40 cm2 B.48 cm2 C.50 cm2 D.60 cm2
7.如图,将一块含30°角的直角三角板放置在平行线a,b之间,且较长直角边靠在直线a上,然后将三角板绕着顶点A逆时针旋转25°后另一个顶点B恰好落在直线b上,这时直角边BC与直线b所构成的∠1的度数为 ( )
A.70° B.65° C.60° D.55°
8.如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将△APC绕着点A逆时针旋转60°得到△AEF,则AE+PB+PC的最小值为 ( )
A.2 B.8 C.5 D.6
二、填空题(每小题4分,共16分)
9.在平面直角坐标系中,将点(2,1)向下平移3个单位长度后得到的点的坐标是 .
10.如图,将直角△ABC(其中∠ABC=60°)绕点B顺时针旋转一个角度到△A'BC'的位置,使得点A,B,C'在同一条直线上,则这个旋转的角度为 .
如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得到∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的度数是 .
如图,△ABC是等边三角形,AB=2,点D在边AB上,且BD=1,E是边AC的中点,将线段BD绕点B顺时针旋转,点D的对应点为F,连接AF,EF,当△AEF为直角三角形时,AF的长为 .
三、解答题(本大题5小题,共52分)
13.(8分)为了美化环境,需在一块正方形的空地上分别种植四种不同的花草.现要将这块空地分割成4块全等图形,且分割后整个图形是中心对称图形.现给出一种画法(如图1),请按上述要求,再画出3种不同的画法.
14.(8分)在图1、图2的网格纸中,△ABC与△DEF的三个顶点都在格点上.
(1)在图1中,以点A为对称中心画一个与△ABC成中心对称的图形;
(2)在图2中,将△DEF绕着点D按顺时针方向旋转90°,画出旋转后的图形.
15.(10分)如图,将线段AB向右平移至线段DC,使点A与点D对应,点B与点C对应,连接AD,BC,∠A=2∠B.
(1)求∠BCD的度数;
(2)若F,G,E依次为BC延长线上的点,且∠EFD=∠EDF,∠FDG=30°,请判断DG是否平分∠CDE,并说明理由.
16.(12分)在如图所示的网格中,每个小三角形均为等边三角形,点A,B,C,D都在格点上.
(1)将△ADC向左平移,使点C与点B重合,画出平移后的△EFB;
(2)将△ADC绕点C逆时针旋转60°,点D的对应点为点G,画出旋转后的三角形;
(3)若点P是△ABC内一点,且满足PA2+PC2=PB2,求∠APC的度数.
17.(14分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,点D是直角边BC所在直线上的一个动点,连接AD,将AD绕点A逆时针旋转60°到AE,连接BE,DE.
(1)如图1,当点E恰好在线段BC上时,请判断线段DE和BE之间的数量关系,并说明理由.
(2)如图2、图3,当点E不在直线BC上时,其他条件不变,(1)中的结论是否成立 若成立,请在图2、图3中选择一个给予证明;若不成立,请直接写出DE和BE之间的数量关系.
参考答案
一、选择题
1 2 3 4 5 6 7 8
A B C B C C B A
3.C 【解析】在△ABC中,∠A=32°,∠B=50°,∴∠ACB=180°-32°-50°=98°,如图,当CB'∥AB时,旋转角=∠B=50°,当CB″∥AB时,∠B″CA=∠A=32°,∴旋转角=360°-32°-98°=230°,综上所述,两个人的结果合在一起才正确.
4.B 【解析】∵点A先向下平移2个单位长度,再向右平移3个单位长度得到点A',点A'恰好与原点重合,∴原点(0,0)先向左平移3个单位长度,再向上平移2个单位长度,得到点A(-3,2).
解题思路 利用平移的性质解决问题即可.
答题妙招 点的平移变换与坐标的变化规律:点(x,y)右(左)平移m个单位长度,得对应点的坐标为(x±m,y),点(x,y)上(下)平移n个单位长度,得对应点的坐标为(x,y±n).根据这些平移规律可以解决很多中考中与坐标系平移有关的问题.
5.C 【解析】∵△OAB绕点O逆时针旋转80°得到△OCD,∴∠BOD=80°,∴∠AOD=∠BOD-∠AOB=80°-35°=45°.
6.C 【解析】∵Rt△ABC沿BC方向平移得到Rt△DEF,∴AB=DE=12 cm,△ABC≌△DEF,∴阴影部分面积=梯形ABEH的面积,∵DH=4 cm,∴EH=12-4=8(cm),∴阴影部分的面积=×(8+12)×5=50(cm2).
7.B 【解析】如图,根据题意,得∠3=∠BAC+25°=25°+30°=55°,∵a∥b,∴∠2=∠3=55°,∵∠1+∠2+∠ABC=180°,∴∠1=180°-55°-60°=65°.
8.A 【解析】如图,连接PE,BF,过点B作AF的垂线交FA的延长线于G,∵△APC绕着点A逆时针旋转60°得到△AEF,∴AP=AE,∠PAE=∠CAF=60°,PC=EF,∴△APE为等边三角形,即AE=PE,∴AE+PB+PC=PB+PE+EF≥BF,∵∠BAC=60°,∴∠BAF=120°,∴∠BAG=60°,∴AG=AB=2,GF=2+6=8,∴BG===2,∴BF===2.
二、填空题
9.(2,-2) 【解析】将点(2,1)向下平移3个单位长度所得点的坐标为(2,1-3),即(2,-2).
10.120° 【解析】由题意可知∠A'BC'=∠ABC=60°,∴这个旋转的角度是∠ABA'=180°-∠A'BC'=180°-60°=120°.
11.105° 【解析】∵∠AOB沿着MN的方向平移一定距离后得到∠CPD,∴BO∥DP,∴∠BON=∠DPN=50°,∴∠AOB=180°-25°-50°=105°.
12.或 【解析】∵△ABC是等边三角形,E是边AC的中点,∴只能是∠AEF=90°,当点F在△ABC内时,∠AEF=90°,此时,点B,F,E三点共线,且点F在点B,E之间,∴BE===3,∴EF=BE-BF=3-1=2,∴AF===;当点F在△ABC外时,∠AEF=90°,此时,点B,F,E三点共线,且点B在点F,E之间,此时,EF=BE+BF=3+1=4,∴AF===.
解题思路 根据题意,判断出只能是∠AEF=90°,分两种情形,点B,F,E三点共线,且点F在点B,E之间,或点B,F,E三点共线,且点B在点F,E之间,分别通过勾股定理求AF的长即可.
易错警示 由于缺乏分类意识而忽略“点B,F,E三点共线,且点B在点F,E之间”的情形,而导致丢值掉解.
【拓展设问】一副三角板按如图所示的方式放置,将三角板ADE绕点A逆时针旋转α(0°<α<90°),使得三角板ADE的一边所在的直线与BC垂直,则α的度数为 .
【答案】15°或60° 分两种情形讨论:当DE⊥BC时,∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;当AD⊥BC时,α=90°-∠C=90°-30°=60°.故α的度数为15°或60°.
答题妙招 解与旋转有关的问题时,由于旋转方向、旋转角度或图形的位置与形状等不确定因素的影响而引发分类讨论,从而造成答案不唯一.
三、解答题
13.解:如图所示. (8分)
14.解:(1)如图1,△AB'C'为所求; (4分)
(2)如图2,△DE'F'为所求. (8分)
15.解:(1)由平移特征,可得AB∥DC,AD∥BC,
∴∠B+∠BCD=180°,∠A+∠B=180°.
∵∠A=2∠B,∴∠B=60°,
∴∠BCD=180°-60°=120°. (4分)
(2)DG平分∠CDE. (5分)
理由:∵AB∥CD,∴∠DCE=∠B=60°.
由三角形的外角性质,得∠CDF=∠DFE-60°,
又∵∠FDG=30°,∴∠CDG=∠CDF+30°=∠DFE-60°+30°=∠DFE-30°.
∵∠EDG=∠EDF-∠FDG=∠EDF-30°,
又∵∠DFE=∠EDF,
∴∠CDG=∠EDG,
∴DG平分∠CDE. (10分)
16.解:(1)如图所示,△EFB为所求; (3分)
(2)如图所示,△BCG为所求; (6分)
(3)如图所示,将△ABP绕点A逆时针旋转60°得到△ACD,连接PD,∴△ADP是等边三角形,CD=BP,∴∠APD=60°,AP=DP,∵PA2+PC2=PB2,∴PD2+PC2=CD2,∴△CPD是直角三角形,∴∠CPD=90°,∴∠APC=∠APD+∠CPD=60°+90°=150°. (12分)
17.解:(1)DE=BE. (1分)
理由:由旋转可知,AD=AE,∠DAE=60°,
∴△ADE为等边三角形,∴DE=AE,∠AED=60°.
∵∠ABC=30°,∠AED=∠ABC+∠EAB,∴∠EAB=60°-30°=30°,∴∠ABC=∠EAB,∴BE=AE,∴DE=BE. (6分)
(2)图2、图3中结论仍成立. (7分)
选择图2证明:如图,过点E作EF⊥AB,垂足为点F.
在Rt△ABC中,∠ACB=90°,∠ABC=30°,
∴∠CAB=60°,∴∠DAE=∠CAB,
∴∠DAE-∠CAE=∠CAB-∠CAE,即∠CAD=∠EAF,又∵AD=AE,∠ACD=∠AFE=90°,∴△ADC≌△AEF(AAS),∴AC=AF.
∵在Rt△ABC中,∠ABC=30°,∴AC=AB,∴AF=AB.
又∵EF⊥AB,∴AE=BE.
由(1)知AE=DE,∴DE=BE. (14分)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
