第一章 三角形的证明 基础闯关卷(含答案) 2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 第一章 三角形的证明 基础闯关卷(含答案) 2024-2025学年北师大版八年级数学下册 | 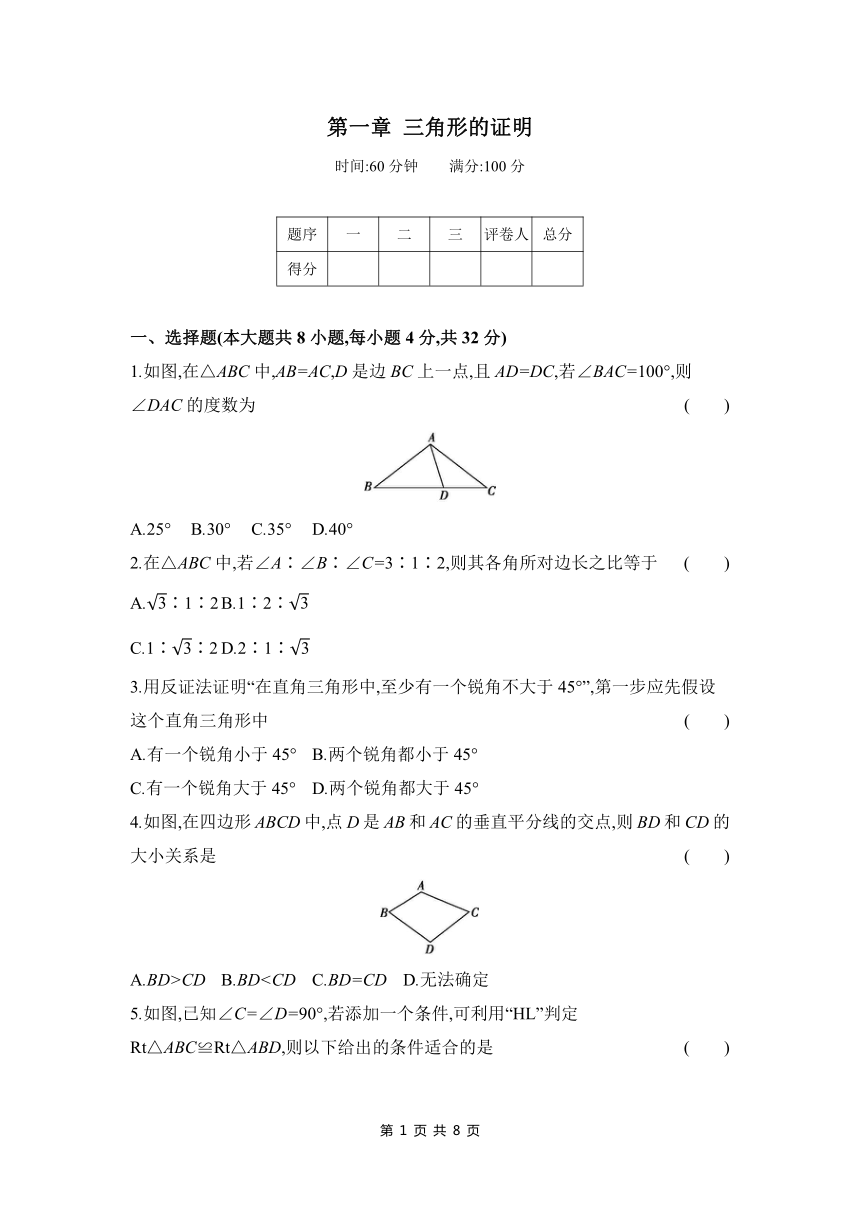 | |
| 格式 | docx | ||
| 文件大小 | 133.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:40:12 | ||
图片预览




文档简介
第一章 三角形的证明
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.如图,在△ABC中,AB=AC,D是边BC上一点,且AD=DC,若∠BAC=100°,则∠DAC的度数为 ( )
A.25° B.30° C.35° D.40°
2.在△ABC中,若∠A∶∠B∶∠C=3∶1∶2,则其各角所对边长之比等于 ( )
A.∶1∶2 B.1∶2∶
C.1∶∶2 D.2∶1∶
3.用反证法证明“在直角三角形中,至少有一个锐角不大于45°”,第一步应先假设这个直角三角形中 ( )
A.有一个锐角小于45° B.两个锐角都小于45°
C.有一个锐角大于45° D.两个锐角都大于45°
4.如图,在四边形ABCD中,点D是AB和AC的垂直平分线的交点,则BD和CD的大小关系是 ( )
A.BD>CD B.BD5.如图,已知∠C=∠D=90°,若添加一个条件,可利用“HL”判定Rt△ABC≌Rt△ABD,则以下给出的条件适合的是 ( )
A.AC=AD B.∠CAB=∠DAB
C.AB=AB D.∠ABC=∠ABD
6.如图,AD是∠BAC的平分线,DE⊥AB于点E,若AB=4 cm,AC=3 cm,点D到AC的距离为2 cm,则△ABC的面积为 ( )
A.7 cm2 B.8 cm2 C.9 cm2 D.10 cm2
7.已知下列三个命题:①等边三角形的三个内角相等;②若a+b=0,则|a|=|b|;③底角相等的两个等腰三角形全等.其中逆命题为真命题的是 ( )
A.①② B.①③ C.②③ D.①②③
8.如图,△ABC和△DCE都是边长为6的等边三角形,点B,C,E在同一条直线上,连接BD,则△BCD的周长为 ( )
A.15 B.12+3 C.12+ D.12+6
二、填空题(每小题4分,共16分)
9.若等腰三角形的一个内角为100°,则底角的度数为 .
10.如图,AB=CD,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,∠D=60°,则∠A的度数为 .
如图,在△ABC中,AB=AC,AB的垂直平分线交边AC于点D,连接BD,若△ABC和△DBC的周长分别是60 cm和38 cm,则AB的长为 cm.
如图,在△ABC中,∠C=90°,∠B=48°,DE⊥AB于点E,且DE=3 cm,BD=5 cm,BC=8 cm,则∠CAD的度数为 .
三、解答题(本大题5小题,共52分)
13.(8分)如图,AC和BD相交于点O,∠A=∠D,OB=OC,求证:∠ABC=∠DCB.
14.(10分)如图,△ABC为等边三角形,点D为边AC的中点,点E为BC的延长线上一点,且BD=DE.
(1)求∠BDE的度数;
(2)若△ABC的周长为6 cm,求BD的长.
15.(10分)如图,点P是∠AOB内的一点,PE⊥OA,PF⊥OB,垂足分别是点E,F,且PE=PF,Q是射线OP上的任意一点,QM⊥OA,QN⊥OB.
(1)求证:QM=QN.
(2)若四边形MONQ的面积为10 cm2,QM=2 cm,求ON的长.
16.(10分)如图,在Rt△ABC中,∠ACB=90°.
(1)尺规作图:请你利用尺规在Rt△ABC的边BC上求作一点P,使得PA=PB.(不写作法,保留作图痕迹)
(2)在你所作的图中,连接AP,若AC=4,BC=8,求△APB的面积.
17.(14分)如图,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,点E是边AC上的一个动点(点E不与点A,C重合),点F是边AB上的一个动点(点F不与点A,B重合),连接EF.
(1)若a,b满足(a-8)2+|b-6|=0,c是一元一次方程=x-4的解,试判断△ABC的形状,并说明理由.
(2)在(1)的条件所得到的△ABC中,若EF平分△ABC的周长,设AE=x,试用含x的代数式表示BF和CE.当x为何值时,CE=BF 此时AF的长为多少
参考答案
一、选择题
1 2 3 4 5 6 7 8
D D D C A A B D
1.D 【解析】∵AB=AC,∠BAC=100°,∴∠B=∠C=40°,∵AD=DC,∴∠DAC=∠C=40°.
2.D 【解析】在△ABC中,∵∠A∶∠B∶∠C=3∶1∶2,∴∠A=90°,∠B=30°,∠C=60°,故△ABC为含30°的角的直角三角形,∴a∶b∶c=2∶1∶.
3.D 【解析】至少有一个锐角不大于45°的反面是两个锐角都大于45°.
4.C 【解析】如图,连接AD,∵点D在AB的垂直平分线上,∴BD=AD,∵点D在AC的垂直平分线上,∴AD=DC,∴BD=CD.
5.A 【解析】图中的两个直角三角形已有斜边AB是公共边相等,因此只需添加一对应直角边相等即可,即添加AC=AD或BC=BD即可.
6.A 【解析】∵AD是∠BAC的平分线,DE⊥AB,∴DE=点D到AC的距离=2 cm,∴S△ABC=S△ACD+S△ABD=×3×2+×4×2=7(cm2).
解题思路 过点D作DF⊥AC,根据角平分线的性质得到DE=DF,再根据三角形的面积公式求取即可.
技巧点拨 在解角平分线作为已知条件的问题时,要注意联想“在角的平分线上的点到这个角的两边的距离相等”这一性质,要形成一种解题意识,从而使解题过程水到渠成.
【拓展设问】如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7 cm2,DE=2 cm,AB=4 cm,则AC的长是 .
【答案】3 cm 如图,作DF⊥AC于点F,
∵AD是△ABC中∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF=2 cm,
∵S△ABC=7 cm2,AB=4 cm,
∴S△ABC=S△ADB+S△ADC=AB·DE+AC·DF=×4×2+×AC×2=7,解得AC=3 cm.
7.B 【解析】①逆命题为三个内角相等的三角形是等边三角形,是真命题;②逆命题是若|a|=|b|,则a+b=0,是假命题;③逆命题为两个全等的等腰三角形的底角相等,是真命题.
8.D 【解析】如图,设BD与AC交于点F,∵△ABC和△DCE都是边长为6的等边三角形,∴BC=CD=6,∠ACB=∠DCE=60°,∴∠DBC=∠CDB=30°,∠ACD=60°,∴AC⊥BD,∴CF=CD=3,∴DF=3,∴BD=6,∴△BCD的周长=6+6+6=12+6.
二、填空题
9.40° 【解析】若100°角为顶角,则底角为40°; 若100°角为底角,三角形的内角和大于180°,则不成立.
10.30° 【解析】∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°,又∵AB=CD,BF=DE,∴△AFB≌△CED(HL),∴∠A=∠C,∴∠A=90°-∠D=90°-60°=30°.
11.22 【解析】∵点D在线段AB的垂直平分线上,∴BD=AD,∴BD+DC+BC=AC+BC=38 cm,又∵AB+AC+BC=60 cm,∴AB=60-38=22(cm).
12.21° 【解析】∵CD=BC-BD=3 cm,DE=3 cm,∴DE=CD,∵CD⊥AC,DE⊥AB,∴AD平分∠BAC,∴∠CAD=∠CAB=×(90°-48°)=21°.
三、解答题
13.证明:∵OB=OC,∴∠OBC=∠OCB,
在△ABC和△DCB中,
∴△ABC≌△DCB(AAS), (6分)
∴∠ABC=∠DCB. (8分)
高分技巧 从作用来看:等腰三角形的性质“等边对等角”是作为两个角相等的依据;而等腰三角形的判定“等角对等边”是说明两条边相等的依据;从数和形来看:如果题目要说明“数量关系”,用性质;如果题目要说明“图形类型”,用判定.
14.解:(1)∵△ABC为等边三角形,∴AB=BC,∠ABC=∠ACB=60°,
∵BD为中线,∴∠CBD=∠ABD=30°,BD⊥AC. (3分)
∵BD=DE,∴∠B=∠E=30°,
∵∠ACB=60°,∴∠CDE=30°,
∴∠BDE=90°+30°=120°. (6分)
(2)∵△ABC的周长为6 cm,∴BC=AC=2 cm,
∵BD为中线,∴CD=1 cm,
∵BD⊥AC,∴BD==(cm). (10分)
15.解:(1)证明:∵PE⊥OA,PF⊥OB,PE=PF,∴OP平分∠AOB, (2分)
∵QM⊥OA,QN⊥OB,∴QM=QN. (3分)
(2)在Rt△OMQ和Rt△ONQ中,
∴Rt△OMQ≌Rt△ONQ(HL),
∴S△OMQ=S△ONQ,OM=ON.
∵四边形MONQ的面积为10 cm2,∴S△ONQ=5 cm2, (6分)
∵QM=QN=2 cm,∴S△ONQ=×ON×QN=×ON×2,
∴×ON×2=5,∴ON=5 cm. (10分)
16.解:(1)如图,点P为所求. (4分)
(2)连接AP,如图所示.
设BP=x,则AP=x,CP=BC-PB=8-x,
在Rt△ACP中,根据勾股定理,得PC2+AC2=AP2,
∴(8-x)2+42=x2,解得x=5,∴BP的长为5. (7分)
∴△APB的面积=AC·BP=×4×5=10. (10分)
17.解:(1)△ABC是直角三角形. (2分)
理由:由非负数的性质得a-8=0,b-6=0,解得a=8,b=6.
解方程=x-4,得x+14=4(x-4),x+14=4x-16,3x=30,∴x=10. (6分)
∵a2+b2=82+62=100,c2=100,∴a2+b2=c2,∴△ABC是直角三角形. (8分)
(2)∵AE+AF=×(6+8+10)=12,∴AF=12-x,∴BF=10-(12-x)=x-2,
∵AC=6,∴CE=6-x. (12分)
当BF=CE时,x-2=6-x,解得x=4,
此时AF=8. (14分)
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共8小题,每小题4分,共32分)
1.如图,在△ABC中,AB=AC,D是边BC上一点,且AD=DC,若∠BAC=100°,则∠DAC的度数为 ( )
A.25° B.30° C.35° D.40°
2.在△ABC中,若∠A∶∠B∶∠C=3∶1∶2,则其各角所对边长之比等于 ( )
A.∶1∶2 B.1∶2∶
C.1∶∶2 D.2∶1∶
3.用反证法证明“在直角三角形中,至少有一个锐角不大于45°”,第一步应先假设这个直角三角形中 ( )
A.有一个锐角小于45° B.两个锐角都小于45°
C.有一个锐角大于45° D.两个锐角都大于45°
4.如图,在四边形ABCD中,点D是AB和AC的垂直平分线的交点,则BD和CD的大小关系是 ( )
A.BD>CD B.BD
A.AC=AD B.∠CAB=∠DAB
C.AB=AB D.∠ABC=∠ABD
6.如图,AD是∠BAC的平分线,DE⊥AB于点E,若AB=4 cm,AC=3 cm,点D到AC的距离为2 cm,则△ABC的面积为 ( )
A.7 cm2 B.8 cm2 C.9 cm2 D.10 cm2
7.已知下列三个命题:①等边三角形的三个内角相等;②若a+b=0,则|a|=|b|;③底角相等的两个等腰三角形全等.其中逆命题为真命题的是 ( )
A.①② B.①③ C.②③ D.①②③
8.如图,△ABC和△DCE都是边长为6的等边三角形,点B,C,E在同一条直线上,连接BD,则△BCD的周长为 ( )
A.15 B.12+3 C.12+ D.12+6
二、填空题(每小题4分,共16分)
9.若等腰三角形的一个内角为100°,则底角的度数为 .
10.如图,AB=CD,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,∠D=60°,则∠A的度数为 .
如图,在△ABC中,AB=AC,AB的垂直平分线交边AC于点D,连接BD,若△ABC和△DBC的周长分别是60 cm和38 cm,则AB的长为 cm.
如图,在△ABC中,∠C=90°,∠B=48°,DE⊥AB于点E,且DE=3 cm,BD=5 cm,BC=8 cm,则∠CAD的度数为 .
三、解答题(本大题5小题,共52分)
13.(8分)如图,AC和BD相交于点O,∠A=∠D,OB=OC,求证:∠ABC=∠DCB.
14.(10分)如图,△ABC为等边三角形,点D为边AC的中点,点E为BC的延长线上一点,且BD=DE.
(1)求∠BDE的度数;
(2)若△ABC的周长为6 cm,求BD的长.
15.(10分)如图,点P是∠AOB内的一点,PE⊥OA,PF⊥OB,垂足分别是点E,F,且PE=PF,Q是射线OP上的任意一点,QM⊥OA,QN⊥OB.
(1)求证:QM=QN.
(2)若四边形MONQ的面积为10 cm2,QM=2 cm,求ON的长.
16.(10分)如图,在Rt△ABC中,∠ACB=90°.
(1)尺规作图:请你利用尺规在Rt△ABC的边BC上求作一点P,使得PA=PB.(不写作法,保留作图痕迹)
(2)在你所作的图中,连接AP,若AC=4,BC=8,求△APB的面积.
17.(14分)如图,在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,点E是边AC上的一个动点(点E不与点A,C重合),点F是边AB上的一个动点(点F不与点A,B重合),连接EF.
(1)若a,b满足(a-8)2+|b-6|=0,c是一元一次方程=x-4的解,试判断△ABC的形状,并说明理由.
(2)在(1)的条件所得到的△ABC中,若EF平分△ABC的周长,设AE=x,试用含x的代数式表示BF和CE.当x为何值时,CE=BF 此时AF的长为多少
参考答案
一、选择题
1 2 3 4 5 6 7 8
D D D C A A B D
1.D 【解析】∵AB=AC,∠BAC=100°,∴∠B=∠C=40°,∵AD=DC,∴∠DAC=∠C=40°.
2.D 【解析】在△ABC中,∵∠A∶∠B∶∠C=3∶1∶2,∴∠A=90°,∠B=30°,∠C=60°,故△ABC为含30°的角的直角三角形,∴a∶b∶c=2∶1∶.
3.D 【解析】至少有一个锐角不大于45°的反面是两个锐角都大于45°.
4.C 【解析】如图,连接AD,∵点D在AB的垂直平分线上,∴BD=AD,∵点D在AC的垂直平分线上,∴AD=DC,∴BD=CD.
5.A 【解析】图中的两个直角三角形已有斜边AB是公共边相等,因此只需添加一对应直角边相等即可,即添加AC=AD或BC=BD即可.
6.A 【解析】∵AD是∠BAC的平分线,DE⊥AB,∴DE=点D到AC的距离=2 cm,∴S△ABC=S△ACD+S△ABD=×3×2+×4×2=7(cm2).
解题思路 过点D作DF⊥AC,根据角平分线的性质得到DE=DF,再根据三角形的面积公式求取即可.
技巧点拨 在解角平分线作为已知条件的问题时,要注意联想“在角的平分线上的点到这个角的两边的距离相等”这一性质,要形成一种解题意识,从而使解题过程水到渠成.
【拓展设问】如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7 cm2,DE=2 cm,AB=4 cm,则AC的长是 .
【答案】3 cm 如图,作DF⊥AC于点F,
∵AD是△ABC中∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF=2 cm,
∵S△ABC=7 cm2,AB=4 cm,
∴S△ABC=S△ADB+S△ADC=AB·DE+AC·DF=×4×2+×AC×2=7,解得AC=3 cm.
7.B 【解析】①逆命题为三个内角相等的三角形是等边三角形,是真命题;②逆命题是若|a|=|b|,则a+b=0,是假命题;③逆命题为两个全等的等腰三角形的底角相等,是真命题.
8.D 【解析】如图,设BD与AC交于点F,∵△ABC和△DCE都是边长为6的等边三角形,∴BC=CD=6,∠ACB=∠DCE=60°,∴∠DBC=∠CDB=30°,∠ACD=60°,∴AC⊥BD,∴CF=CD=3,∴DF=3,∴BD=6,∴△BCD的周长=6+6+6=12+6.
二、填空题
9.40° 【解析】若100°角为顶角,则底角为40°; 若100°角为底角,三角形的内角和大于180°,则不成立.
10.30° 【解析】∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°,又∵AB=CD,BF=DE,∴△AFB≌△CED(HL),∴∠A=∠C,∴∠A=90°-∠D=90°-60°=30°.
11.22 【解析】∵点D在线段AB的垂直平分线上,∴BD=AD,∴BD+DC+BC=AC+BC=38 cm,又∵AB+AC+BC=60 cm,∴AB=60-38=22(cm).
12.21° 【解析】∵CD=BC-BD=3 cm,DE=3 cm,∴DE=CD,∵CD⊥AC,DE⊥AB,∴AD平分∠BAC,∴∠CAD=∠CAB=×(90°-48°)=21°.
三、解答题
13.证明:∵OB=OC,∴∠OBC=∠OCB,
在△ABC和△DCB中,
∴△ABC≌△DCB(AAS), (6分)
∴∠ABC=∠DCB. (8分)
高分技巧 从作用来看:等腰三角形的性质“等边对等角”是作为两个角相等的依据;而等腰三角形的判定“等角对等边”是说明两条边相等的依据;从数和形来看:如果题目要说明“数量关系”,用性质;如果题目要说明“图形类型”,用判定.
14.解:(1)∵△ABC为等边三角形,∴AB=BC,∠ABC=∠ACB=60°,
∵BD为中线,∴∠CBD=∠ABD=30°,BD⊥AC. (3分)
∵BD=DE,∴∠B=∠E=30°,
∵∠ACB=60°,∴∠CDE=30°,
∴∠BDE=90°+30°=120°. (6分)
(2)∵△ABC的周长为6 cm,∴BC=AC=2 cm,
∵BD为中线,∴CD=1 cm,
∵BD⊥AC,∴BD==(cm). (10分)
15.解:(1)证明:∵PE⊥OA,PF⊥OB,PE=PF,∴OP平分∠AOB, (2分)
∵QM⊥OA,QN⊥OB,∴QM=QN. (3分)
(2)在Rt△OMQ和Rt△ONQ中,
∴Rt△OMQ≌Rt△ONQ(HL),
∴S△OMQ=S△ONQ,OM=ON.
∵四边形MONQ的面积为10 cm2,∴S△ONQ=5 cm2, (6分)
∵QM=QN=2 cm,∴S△ONQ=×ON×QN=×ON×2,
∴×ON×2=5,∴ON=5 cm. (10分)
16.解:(1)如图,点P为所求. (4分)
(2)连接AP,如图所示.
设BP=x,则AP=x,CP=BC-PB=8-x,
在Rt△ACP中,根据勾股定理,得PC2+AC2=AP2,
∴(8-x)2+42=x2,解得x=5,∴BP的长为5. (7分)
∴△APB的面积=AC·BP=×4×5=10. (10分)
17.解:(1)△ABC是直角三角形. (2分)
理由:由非负数的性质得a-8=0,b-6=0,解得a=8,b=6.
解方程=x-4,得x+14=4(x-4),x+14=4x-16,3x=30,∴x=10. (6分)
∵a2+b2=82+62=100,c2=100,∴a2+b2=c2,∴△ABC是直角三角形. (8分)
(2)∵AE+AF=×(6+8+10)=12,∴AF=12-x,∴BF=10-(12-x)=x-2,
∵AC=6,∴CE=6-x. (12分)
当BF=CE时,x-2=6-x,解得x=4,
此时AF=8. (14分)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
