期中测试闯关卷(第1-3章)(含答案) 2024-2025学年北师大版八年级数学下册
文档属性
| 名称 | 期中测试闯关卷(第1-3章)(含答案) 2024-2025学年北师大版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 241.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:42:08 | ||
图片预览



文档简介
期中测试卷
考试范围:第一章~第三章
时间:90分钟 满分:120分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.给出下列命题:①若a>b,则ac2>bc2;②若ab>c,则b>;③若-3a>2a,则a<0;④若aA.③④ B.①③ C.①② D.②④
2.下列关于△ABC与△A'B'C'的几何变换中,配对正确的是 ( )
Ⅰ.轴对称;Ⅱ.中心对称;Ⅲ.旋转;Ⅳ.平移.
A.①-Ⅰ,②-Ⅱ,③-Ⅲ,④-Ⅳ
B.①-Ⅱ,②-Ⅰ,③-Ⅲ,④-Ⅲ
C.①-Ⅱ,②-Ⅰ,③-Ⅲ,④-Ⅳ
D.①-Ⅰ,②-Ⅱ,③-Ⅲ,④-Ⅲ
3.将点A(-2,3)通过平移得到点A'(-5,7),以下方式正确的是 ( )
A.沿x轴向右平移3个单位长度,再沿y轴向上平移4个单位长度
B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度
C.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度
D.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度
4.如图,函数y1=-x-1与y2=ax-3的图象相交于点P(m,-2),则关于x的不等式-x-1A.x<2 B.x<1
C.x>2 D.x>1
5.如图,在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=6,DE=2,则△BCE的面积为 ( )
A.12 B.10 C.8 D.6
6.如图,在△ABC中,AB=BC,∠A=36°,AB的垂直平分线DE交AB于点D,交AC于点E,若AB=10,则CE的长为 ( )
A.5 B.8 C.10 D.10
7.已知关于x的不等式组的最小整数解是2,则实数m的取值范围是 ( )
A.-3C.-38.如图,在Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB',连接B'C,则△AB'C的面积为 ( )
A.4 B.6 C.8 D.10
9.为了解决部分家长在放学时间不能按时接送孩子的问题,我市许多学校都启动了“课后服务”工作.某学校为了开展好“课后服务”工作,计划用不超过10 000元的资金购买足球、篮球和排球用于球类兴趣班.已知足球、篮球、排球的单价分别为100元、80元、60元,且根据参加各类球类兴趣班的学生人数了解到以下两项信息:①篮球的数量必须比足球多10个;②排球的数量必须是足球的3倍.则学校最多能购买足球的个数为 ( )
A.100 B.25 C.26 D.30
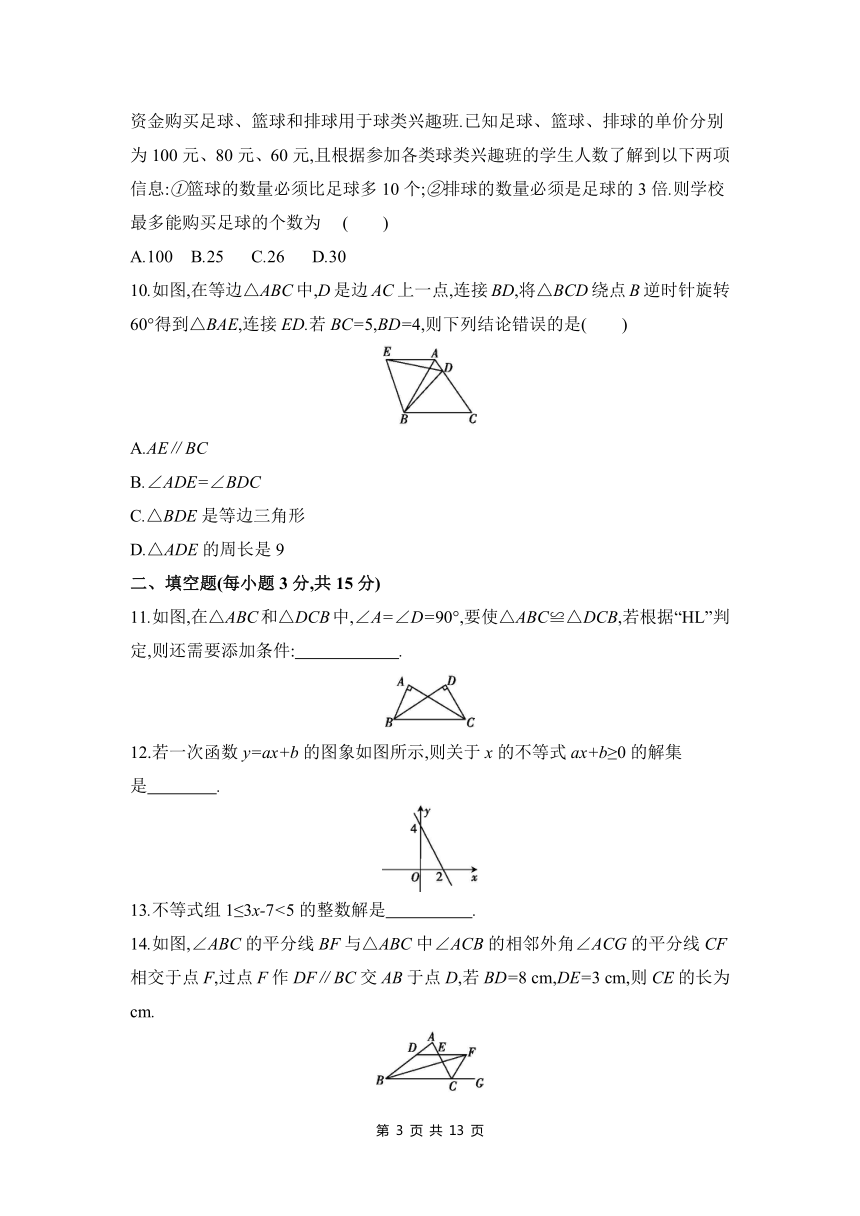
10.如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=5,BD=4,则下列结论错误的是( )
A.AE∥BC
B.∠ADE=∠BDC
C.△BDE是等边三角形
D.△ADE的周长是9
二、填空题(每小题3分,共15分)
11.如图,在△ABC和△DCB中,∠A=∠D=90°,要使△ABC≌△DCB,若根据“HL”判定,则还需要添加条件: .
12.若一次函数y=ax+b的图象如图所示,则关于x的不等式ax+b≥0的解集是 .
13.不等式组1≤3x-7<5的整数解是 .
14.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过点F作DF∥BC交AB于点D,若BD=8 cm,DE=3 cm,则CE的长为 cm.
15.如图,点O是等边△ABC内一点,∠AOB=110°.将△BOC绕点C顺时针旋转60°得到△ADC,连接OD.若△AOD是等腰三角形,则∠BOC的度数为 .
三、解答题(本大题共8个小题,满分75分)
16.(10分)(1)解不等式:-≤2.
(2)如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=2,求AC的长.
17.(9分)解不等式组并写出不等式组的整数解.
18.(9分)如图,在由边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点)与点O.
(1)将△ABC先向下平移4个单位长度,再向右平移4个单位长度得到△A1B1C1,画出平移后的图形;
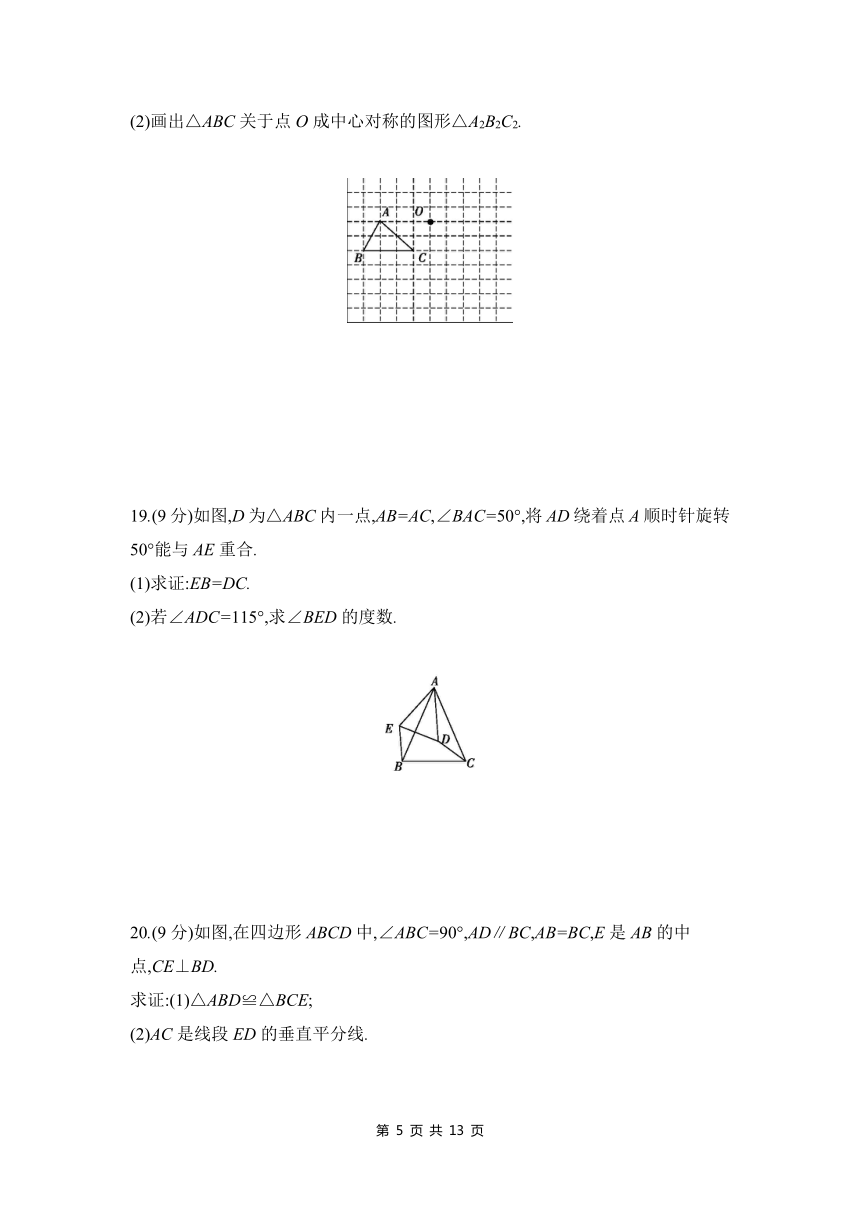
(2)画出△ABC关于点O成中心对称的图形△A2B2C2.
19.(9分)如图,D为△ABC内一点,AB=AC,∠BAC=50°,将AD绕着点A顺时针旋转50°能与AE重合.
(1)求证:EB=DC.
(2)若∠ADC=115°,求∠BED的度数.
20.(9分)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.
求证:(1)△ABD≌△BCE;
(2)AC是线段ED的垂直平分线.
21.(9分)甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.设小红在同一商场累计购物x元,其中x>100.
(1)根据题意,填写下表(单位:元):
(2)当小红在同一商场累计购物超过100元时,在哪家商场的实际花费少
22.(10分)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上运动,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断DE与DP的位置关系,并说明理由;
(2)若AC=6,BC=8,PA=2,求DE的长.
23.(10分)如图,在△ABC中,∠ACB=90°,∠BAC=30°,BC=2,将△ABC绕点C按逆时针方向旋转α(0°<α<90°)得到△DEC,设CD交AB于点F,连接AD.
(1)当α=30°时,回答下列问题:
①求证:△BCF是等边三角形.
②求DF的长及△ADF的面积.(结果保留根号)
(2)当旋转角α为何值时,△ADF是等腰三角形
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
A B C D D C A C B B
1.A 【解析】①当c=0时,不成立,故错误;②当a<0时,不等号方向应改变为b<,故错误;③正确;④正确.
2.B 【解析】观察图象可知:①是中心对称,②是轴对称,③是旋转变换,④是旋转变换.
3.C 【解析】由点A(-2,3),A'(-5,7)可知,横坐标减3,纵坐标加4,∴点A沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度可得到点A'.
4.D 【解析】∵函数y1=-x-1与y2=ax-3的图象相交于点P(m,-2),∴-2=-m-1,解得m=1,故关于x的不等式-x-11.
5.D 【解析】如图,过点E作EF⊥BC于点F,∵BE平分∠DBC,DE⊥AB,EF⊥BC,∴EF=DE=2,∴S△BCE=BC·EF=×6×2=6.
6.C 【解析】∵在△ABC中,AB=BC=10,∠A=36°,∴∠C=∠A=36°,∠ABC=108°,∵AB的垂直平分线是DE,∴AE=BE,∴∠ABE=∠A=36°,∴∠EBC=∠ABC-∠ABE=108°-36°=72°,∵∠BEC=∠A+∠ABE=72°,∴∠BEC=∠EBC,∴CE=BC=10.
7.A 【解析】解不等式≥2,得x≥4+m,解不等式x-4≤3(x-2),得x≥1,∵不等式组的最小整数解是2,∴1<4+m≤2,解得-38.C 【解析】如图,过点B'作B'E⊥AC于点E,由题意可知AB=AB',∠BAB'=90°,∴∠BAC+∠B'AC=90°,且∠B'AC+∠AB'E=90°,∴∠BAC=∠AB'E,且∠ACB=∠AEB'=90°,AB=AB',∴△ABC≌△B'AE(AAS),∴B'E=AC=4,∴S△AB'C=AC·B'E=×4×4=8.
9.B 【解析】设购买足球x个,则购买篮球(x+10)个,排球3x个,由题意,得100x+80(x+10)+60×3x≤10 000,解得x≤25,∵x需为正整数,∴x最大取25.
解题思路 设购买足球x个,则购买篮球(x+10)个,排球3x个,由计划用不超过10 000元的资金购买足球、篮球和排球,列出不等式,即可求解.
【拓展设问】某校团员代表在3月份“学雷锋”活动中购买点心与水果去敬老院慰问15名孤寡老人,其中要求给每位老人50元的慰问金,此次活动的经费不超过990元,则最多可以给每位老人准备用于购买点心与水果的费用为 ( )
A.15元 B.16元
C.17元 D.18元
【答案】B 设给每位老人准备用于购买点心与水果的费用为x元,根据题意得50×15+15x≤990,解得x≤16,∴x的最大值为16,即最多可以给每位老人准备用于购买点心与水果的费用为16元.
技巧点拨 根据实际问题的意义列不等式的关键在于仔细分析问题情境中的不等量关系,注意捕捉表示不等关系的关键性词语,要能熟练地用含一个未知量的代数式表示出另一个量,这里要求有扎实的列代数式的数学功底.
10.B 【解析】∵△ABC是等边三角形,∴∠ABC=∠C=60°,∵将△BCD绕点B逆时针旋转60°得到△BAE,∴∠EAB=∠C=∠ABC=60°,∴AE∥BC,故选项A正确;∵△ABC是等边三角形,∴AC=AB=BC=5,由旋转可知AE=CD,BD=BE,∠EBD=60°,∴AE+AD=AD+CD=AC=5,∵∠EBD=60°,BE=BD,∴△BDE是等边三角形,故选项C正确;∴DE=BD=4,∴△AED的周长=AE+AD+DE=AC+BD=9,故选项D正确;而选项B没有条件证明∠ADE=∠BDC,∴结论错误的是选项B.
二、填空题
11.AB=DC(或AC=DB)
12.x≤2 【解析】函数y=ax+b的图象经过点(2,0),函数值y随x的增大而减小,所以关于x的不等式ax+b≥0的解集为x≤2.
13.3 【解析】根据不等式的性质,得8≤3x<12,即≤x<4,所以其整数解是3.
14.5 【解析】∵BF平分∠ABC,∴∠ABF=∠CBF,∵DF∥BC,∴∠DFB=∠CBF,∴∠ABF=∠DFB,∴BD=DF=8 cm,同理,CE=EF,∵EF=DF-DE=5 cm,∴CE=5 cm.
解题思路 “角平分线+平行线”必有等腰三角形,故可以通过等角对等边,证明△DBF,△ECF均为等腰三角形,即DB=DF,CE=EF,再利用EF=DF-DE,即可解决.
【真题探源】这道题来自北师大八年级《数学》(下)第9页随堂练习第1题:如图,在△ABC中,BD平分∠ABC,交AC于点D,过点D作BC的平行线,交AB于点E,请判断△BDE的形状,并说明理由.
模型分析 角平分线遇上平行线,一定会产生等腰三角形,即“平行线+角平分线=等腰三角形”.要形成一种解题意识,从而使解题过程水到渠成.
15.125°或110°或140° 【解析】设∠BOC=α,由旋转的性质得∠CDA=∠BOC=α,∠OCD=60°,CO=CD,∴△OCD是等边三角形,∴∠COD=∠CDO=60°,∴∠ADO=∠ADC-∠CDO=α-60°,∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-α-60°=190°-α,∴∠OAD=180°-∠ADO-∠AOD=180°-(α-60°)-(190°-α)=50°.分以下三种情况讨论:①当AO=AD时,∠AOD=∠ADO,即190°-α=α-60°,解得α=125°;②当OA=OD时,∠OAD=∠ADO,即60°-α=50°,解得α=110°;③当OD=AD时,∠OAD=∠AOD,即190°-α=50°,解得α=140°.
三、解答题
16.(1)解:去分母,得4(x+17)-3(3x-7)≤24.
去括号,得4x+68-9x+21≤24.
移项、合并同类项,得-5x≤-65.
系数化为1,得 x≥13. (5分)
(2)解:∵在△ABC中,∠C=90°,∠B=30°,
∴∠BAC=60°,
∵AD平分∠BAC,∴∠DAC=30°,
∵CD=1,∴AD=2,
∴AC==. (10分)
17.解:解不等式①,得 x≥-1. (3分)
解不等式②,得 x<3. (6分)
∴不等式组的解集为-1≤x<3.
∴不等式组的整数解是-1,0,1,2. (9分)
18.解:(1)如图所示,△A1B1C1为所求. (4分)
(2)如图所示,△A2B2C2为所求. (9分)
19.解:(1)证明:∵将AD绕着点A顺时针旋转50°能与AE重合,∴AD=AE,∠DAE=50°,∴∠DAE=∠BAC,∴∠CAD=∠BAE,
在△ACD和△ABE中,
∴△ACD≌△ABE(SAS),∴BE=CD. (5分)
(2)由△ACD≌△ABE,得∠ADC=∠AEB=115°,
∵AD=AE,∠DAE=50°,∴∠AED=65°,
∴∠BED=50°. (9分)
20.证明:(1)如图,∵∠ABC=90°,BD⊥EC,∴∠1+∠3=90°,∠2+∠3=90°,∴∠1=∠2,
∵AD∥BC,∴∠BAD=∠ABC=90°.
在△ABD和△BCE中,
∴△ABD≌△BCE(ASA). (4分)
(2)∵E是AB中点,∴EB=EA,
∵△BAD≌△CBE,∴AD=BE,∴AE=AD,
∵AD∥BC,∴∠5=∠ACB=45°,
∵∠4=45°,∴∠4=∠5,
又∵AD=AE,∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线. (9分)
21.解:(1)在甲商场:271,0.9x+10.在乙商场:278,0.95x+25. (4分)
(2)①0.9x+10<0.95x+2.5,解得x>150;
②0.9x+10=0.95x+2.5,解得x=150;
③0.9x+10>0.95x+2.5,解得x<150.
∴当小红累计购物超过150元时,在甲商场的实际花费少;当小红累计购物等于150元时,在甲、乙两商场的实际花费相同;当小红累计购物超过100元但不超过150元时,在乙商场的实际花费少. (9分)
22.解:(1)DE⊥DP. (1分)
理由:∵PA=PD,∴∠A=∠PDA,
∵EF是BD的垂直平分线,∴EB=ED,
∴∠B=∠EDB,∵∠C=90°,∴∠A+∠B=90°,∴∠PDA+∠EDB=90°,∴∠PDE=180°-90°=90°,∴DE⊥DP. (4分)
(2)如图,连接PE,设DE=x,则DE=BE=x,CE=8-x,
∵∠C=∠PDE=90°,∴PC2+CE2=PD2+DE2=PE2,∴42+(8-x)2=22+x2,解得x=4.75,
∴DE的长为4.75. (10分)
23.解:(1)①证明:∵∠ACB=90°,∠BAC=30°,α=30°,∴∠ABC=∠BCF=60°,
∴△BCF是等边三角形. (2分)
②在Rt△ABC中,∵BC=2,∠BAC=30°,∴AB=2BC=4,AC==2,
∵△DEC是由△ABC旋转得到的,
∴DC=AC=2,
由①知CF=BC=2,∴DF=DC-CF=2-2; (4分)
如图,过点A作AP⊥DF于点P,
在Rt△ACP中,∵α=30°,AC=2,∴AP=AC=,
∴S△ADF=DF·AP=×(2-2)×=3-. (6分)
(2)∵AC=CD,∴∠ADF=∠DAC=(180°-α),∴∠DAF=∠DAC-∠BAC=(180°-α)-30°,
根据三角形的外角性质可知∠AFD=∠BAC+∠DCA=30°+α,
∴当△ADF是等腰三角形时,分三种情况讨论:
第一种情况:当∠ADF=∠DAF时,(180°-α)=(180°-α)-30°,无解.
第二种情况:当∠ADF=∠AFD时,(180°-α)=30°+α,解得α=40°.
第三种情况:当∠DAF=∠AFD时,(180°-α)-30°=30°+α,解得α=20°.
综上所述,旋转角α的度数为20°或40°时,△ADF是等腰三角形. (10分)
考试范围:第一章~第三章
时间:90分钟 满分:120分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.给出下列命题:①若a>b,则ac2>bc2;②若ab>c,则b>;③若-3a>2a,则a<0;④若a
2.下列关于△ABC与△A'B'C'的几何变换中,配对正确的是 ( )
Ⅰ.轴对称;Ⅱ.中心对称;Ⅲ.旋转;Ⅳ.平移.
A.①-Ⅰ,②-Ⅱ,③-Ⅲ,④-Ⅳ
B.①-Ⅱ,②-Ⅰ,③-Ⅲ,④-Ⅲ
C.①-Ⅱ,②-Ⅰ,③-Ⅲ,④-Ⅳ
D.①-Ⅰ,②-Ⅱ,③-Ⅲ,④-Ⅲ
3.将点A(-2,3)通过平移得到点A'(-5,7),以下方式正确的是 ( )
A.沿x轴向右平移3个单位长度,再沿y轴向上平移4个单位长度
B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度
C.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度
D.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度
4.如图,函数y1=-x-1与y2=ax-3的图象相交于点P(m,-2),则关于x的不等式-x-1
C.x>2 D.x>1
5.如图,在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=6,DE=2,则△BCE的面积为 ( )
A.12 B.10 C.8 D.6
6.如图,在△ABC中,AB=BC,∠A=36°,AB的垂直平分线DE交AB于点D,交AC于点E,若AB=10,则CE的长为 ( )
A.5 B.8 C.10 D.10
7.已知关于x的不等式组的最小整数解是2,则实数m的取值范围是 ( )
A.-3
A.4 B.6 C.8 D.10
9.为了解决部分家长在放学时间不能按时接送孩子的问题,我市许多学校都启动了“课后服务”工作.某学校为了开展好“课后服务”工作,计划用不超过10 000元的资金购买足球、篮球和排球用于球类兴趣班.已知足球、篮球、排球的单价分别为100元、80元、60元,且根据参加各类球类兴趣班的学生人数了解到以下两项信息:①篮球的数量必须比足球多10个;②排球的数量必须是足球的3倍.则学校最多能购买足球的个数为 ( )
A.100 B.25 C.26 D.30
10.如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=5,BD=4,则下列结论错误的是( )
A.AE∥BC
B.∠ADE=∠BDC
C.△BDE是等边三角形
D.△ADE的周长是9
二、填空题(每小题3分,共15分)
11.如图,在△ABC和△DCB中,∠A=∠D=90°,要使△ABC≌△DCB,若根据“HL”判定,则还需要添加条件: .
12.若一次函数y=ax+b的图象如图所示,则关于x的不等式ax+b≥0的解集是 .
13.不等式组1≤3x-7<5的整数解是 .
14.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过点F作DF∥BC交AB于点D,若BD=8 cm,DE=3 cm,则CE的长为 cm.
15.如图,点O是等边△ABC内一点,∠AOB=110°.将△BOC绕点C顺时针旋转60°得到△ADC,连接OD.若△AOD是等腰三角形,则∠BOC的度数为 .
三、解答题(本大题共8个小题,满分75分)
16.(10分)(1)解不等式:-≤2.
(2)如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=2,求AC的长.
17.(9分)解不等式组并写出不等式组的整数解.
18.(9分)如图,在由边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点)与点O.
(1)将△ABC先向下平移4个单位长度,再向右平移4个单位长度得到△A1B1C1,画出平移后的图形;
(2)画出△ABC关于点O成中心对称的图形△A2B2C2.
19.(9分)如图,D为△ABC内一点,AB=AC,∠BAC=50°,将AD绕着点A顺时针旋转50°能与AE重合.
(1)求证:EB=DC.
(2)若∠ADC=115°,求∠BED的度数.
20.(9分)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.
求证:(1)△ABD≌△BCE;
(2)AC是线段ED的垂直平分线.
21.(9分)甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.设小红在同一商场累计购物x元,其中x>100.
(1)根据题意,填写下表(单位:元):
(2)当小红在同一商场累计购物超过100元时,在哪家商场的实际花费少
22.(10分)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上运动,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断DE与DP的位置关系,并说明理由;
(2)若AC=6,BC=8,PA=2,求DE的长.
23.(10分)如图,在△ABC中,∠ACB=90°,∠BAC=30°,BC=2,将△ABC绕点C按逆时针方向旋转α(0°<α<90°)得到△DEC,设CD交AB于点F,连接AD.
(1)当α=30°时,回答下列问题:
①求证:△BCF是等边三角形.
②求DF的长及△ADF的面积.(结果保留根号)
(2)当旋转角α为何值时,△ADF是等腰三角形
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
A B C D D C A C B B
1.A 【解析】①当c=0时,不成立,故错误;②当a<0时,不等号方向应改变为b<,故错误;③正确;④正确.
2.B 【解析】观察图象可知:①是中心对称,②是轴对称,③是旋转变换,④是旋转变换.
3.C 【解析】由点A(-2,3),A'(-5,7)可知,横坐标减3,纵坐标加4,∴点A沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度可得到点A'.
4.D 【解析】∵函数y1=-x-1与y2=ax-3的图象相交于点P(m,-2),∴-2=-m-1,解得m=1,故关于x的不等式-x-1
5.D 【解析】如图,过点E作EF⊥BC于点F,∵BE平分∠DBC,DE⊥AB,EF⊥BC,∴EF=DE=2,∴S△BCE=BC·EF=×6×2=6.
6.C 【解析】∵在△ABC中,AB=BC=10,∠A=36°,∴∠C=∠A=36°,∠ABC=108°,∵AB的垂直平分线是DE,∴AE=BE,∴∠ABE=∠A=36°,∴∠EBC=∠ABC-∠ABE=108°-36°=72°,∵∠BEC=∠A+∠ABE=72°,∴∠BEC=∠EBC,∴CE=BC=10.
7.A 【解析】解不等式≥2,得x≥4+m,解不等式x-4≤3(x-2),得x≥1,∵不等式组的最小整数解是2,∴1<4+m≤2,解得-3
9.B 【解析】设购买足球x个,则购买篮球(x+10)个,排球3x个,由题意,得100x+80(x+10)+60×3x≤10 000,解得x≤25,∵x需为正整数,∴x最大取25.
解题思路 设购买足球x个,则购买篮球(x+10)个,排球3x个,由计划用不超过10 000元的资金购买足球、篮球和排球,列出不等式,即可求解.
【拓展设问】某校团员代表在3月份“学雷锋”活动中购买点心与水果去敬老院慰问15名孤寡老人,其中要求给每位老人50元的慰问金,此次活动的经费不超过990元,则最多可以给每位老人准备用于购买点心与水果的费用为 ( )
A.15元 B.16元
C.17元 D.18元
【答案】B 设给每位老人准备用于购买点心与水果的费用为x元,根据题意得50×15+15x≤990,解得x≤16,∴x的最大值为16,即最多可以给每位老人准备用于购买点心与水果的费用为16元.
技巧点拨 根据实际问题的意义列不等式的关键在于仔细分析问题情境中的不等量关系,注意捕捉表示不等关系的关键性词语,要能熟练地用含一个未知量的代数式表示出另一个量,这里要求有扎实的列代数式的数学功底.
10.B 【解析】∵△ABC是等边三角形,∴∠ABC=∠C=60°,∵将△BCD绕点B逆时针旋转60°得到△BAE,∴∠EAB=∠C=∠ABC=60°,∴AE∥BC,故选项A正确;∵△ABC是等边三角形,∴AC=AB=BC=5,由旋转可知AE=CD,BD=BE,∠EBD=60°,∴AE+AD=AD+CD=AC=5,∵∠EBD=60°,BE=BD,∴△BDE是等边三角形,故选项C正确;∴DE=BD=4,∴△AED的周长=AE+AD+DE=AC+BD=9,故选项D正确;而选项B没有条件证明∠ADE=∠BDC,∴结论错误的是选项B.
二、填空题
11.AB=DC(或AC=DB)
12.x≤2 【解析】函数y=ax+b的图象经过点(2,0),函数值y随x的增大而减小,所以关于x的不等式ax+b≥0的解集为x≤2.
13.3 【解析】根据不等式的性质,得8≤3x<12,即≤x<4,所以其整数解是3.
14.5 【解析】∵BF平分∠ABC,∴∠ABF=∠CBF,∵DF∥BC,∴∠DFB=∠CBF,∴∠ABF=∠DFB,∴BD=DF=8 cm,同理,CE=EF,∵EF=DF-DE=5 cm,∴CE=5 cm.
解题思路 “角平分线+平行线”必有等腰三角形,故可以通过等角对等边,证明△DBF,△ECF均为等腰三角形,即DB=DF,CE=EF,再利用EF=DF-DE,即可解决.
【真题探源】这道题来自北师大八年级《数学》(下)第9页随堂练习第1题:如图,在△ABC中,BD平分∠ABC,交AC于点D,过点D作BC的平行线,交AB于点E,请判断△BDE的形状,并说明理由.
模型分析 角平分线遇上平行线,一定会产生等腰三角形,即“平行线+角平分线=等腰三角形”.要形成一种解题意识,从而使解题过程水到渠成.
15.125°或110°或140° 【解析】设∠BOC=α,由旋转的性质得∠CDA=∠BOC=α,∠OCD=60°,CO=CD,∴△OCD是等边三角形,∴∠COD=∠CDO=60°,∴∠ADO=∠ADC-∠CDO=α-60°,∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-α-60°=190°-α,∴∠OAD=180°-∠ADO-∠AOD=180°-(α-60°)-(190°-α)=50°.分以下三种情况讨论:①当AO=AD时,∠AOD=∠ADO,即190°-α=α-60°,解得α=125°;②当OA=OD时,∠OAD=∠ADO,即60°-α=50°,解得α=110°;③当OD=AD时,∠OAD=∠AOD,即190°-α=50°,解得α=140°.
三、解答题
16.(1)解:去分母,得4(x+17)-3(3x-7)≤24.
去括号,得4x+68-9x+21≤24.
移项、合并同类项,得-5x≤-65.
系数化为1,得 x≥13. (5分)
(2)解:∵在△ABC中,∠C=90°,∠B=30°,
∴∠BAC=60°,
∵AD平分∠BAC,∴∠DAC=30°,
∵CD=1,∴AD=2,
∴AC==. (10分)
17.解:解不等式①,得 x≥-1. (3分)
解不等式②,得 x<3. (6分)
∴不等式组的解集为-1≤x<3.
∴不等式组的整数解是-1,0,1,2. (9分)
18.解:(1)如图所示,△A1B1C1为所求. (4分)
(2)如图所示,△A2B2C2为所求. (9分)
19.解:(1)证明:∵将AD绕着点A顺时针旋转50°能与AE重合,∴AD=AE,∠DAE=50°,∴∠DAE=∠BAC,∴∠CAD=∠BAE,
在△ACD和△ABE中,
∴△ACD≌△ABE(SAS),∴BE=CD. (5分)
(2)由△ACD≌△ABE,得∠ADC=∠AEB=115°,
∵AD=AE,∠DAE=50°,∴∠AED=65°,
∴∠BED=50°. (9分)
20.证明:(1)如图,∵∠ABC=90°,BD⊥EC,∴∠1+∠3=90°,∠2+∠3=90°,∴∠1=∠2,
∵AD∥BC,∴∠BAD=∠ABC=90°.
在△ABD和△BCE中,
∴△ABD≌△BCE(ASA). (4分)
(2)∵E是AB中点,∴EB=EA,
∵△BAD≌△CBE,∴AD=BE,∴AE=AD,
∵AD∥BC,∴∠5=∠ACB=45°,
∵∠4=45°,∴∠4=∠5,
又∵AD=AE,∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线. (9分)
21.解:(1)在甲商场:271,0.9x+10.在乙商场:278,0.95x+25. (4分)
(2)①0.9x+10<0.95x+2.5,解得x>150;
②0.9x+10=0.95x+2.5,解得x=150;
③0.9x+10>0.95x+2.5,解得x<150.
∴当小红累计购物超过150元时,在甲商场的实际花费少;当小红累计购物等于150元时,在甲、乙两商场的实际花费相同;当小红累计购物超过100元但不超过150元时,在乙商场的实际花费少. (9分)
22.解:(1)DE⊥DP. (1分)
理由:∵PA=PD,∴∠A=∠PDA,
∵EF是BD的垂直平分线,∴EB=ED,
∴∠B=∠EDB,∵∠C=90°,∴∠A+∠B=90°,∴∠PDA+∠EDB=90°,∴∠PDE=180°-90°=90°,∴DE⊥DP. (4分)
(2)如图,连接PE,设DE=x,则DE=BE=x,CE=8-x,
∵∠C=∠PDE=90°,∴PC2+CE2=PD2+DE2=PE2,∴42+(8-x)2=22+x2,解得x=4.75,
∴DE的长为4.75. (10分)
23.解:(1)①证明:∵∠ACB=90°,∠BAC=30°,α=30°,∴∠ABC=∠BCF=60°,
∴△BCF是等边三角形. (2分)
②在Rt△ABC中,∵BC=2,∠BAC=30°,∴AB=2BC=4,AC==2,
∵△DEC是由△ABC旋转得到的,
∴DC=AC=2,
由①知CF=BC=2,∴DF=DC-CF=2-2; (4分)
如图,过点A作AP⊥DF于点P,
在Rt△ACP中,∵α=30°,AC=2,∴AP=AC=,
∴S△ADF=DF·AP=×(2-2)×=3-. (6分)
(2)∵AC=CD,∴∠ADF=∠DAC=(180°-α),∴∠DAF=∠DAC-∠BAC=(180°-α)-30°,
根据三角形的外角性质可知∠AFD=∠BAC+∠DCA=30°+α,
∴当△ADF是等腰三角形时,分三种情况讨论:
第一种情况:当∠ADF=∠DAF时,(180°-α)=(180°-α)-30°,无解.
第二种情况:当∠ADF=∠AFD时,(180°-α)=30°+α,解得α=40°.
第三种情况:当∠DAF=∠AFD时,(180°-α)-30°=30°+α,解得α=20°.
综上所述,旋转角α的度数为20°或40°时,△ADF是等腰三角形. (10分)
同课章节目录
