圆周角
图片预览




文档简介
课件13张PPT。圆周角九年级数学特征:① 角的顶点在圆上.1、圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
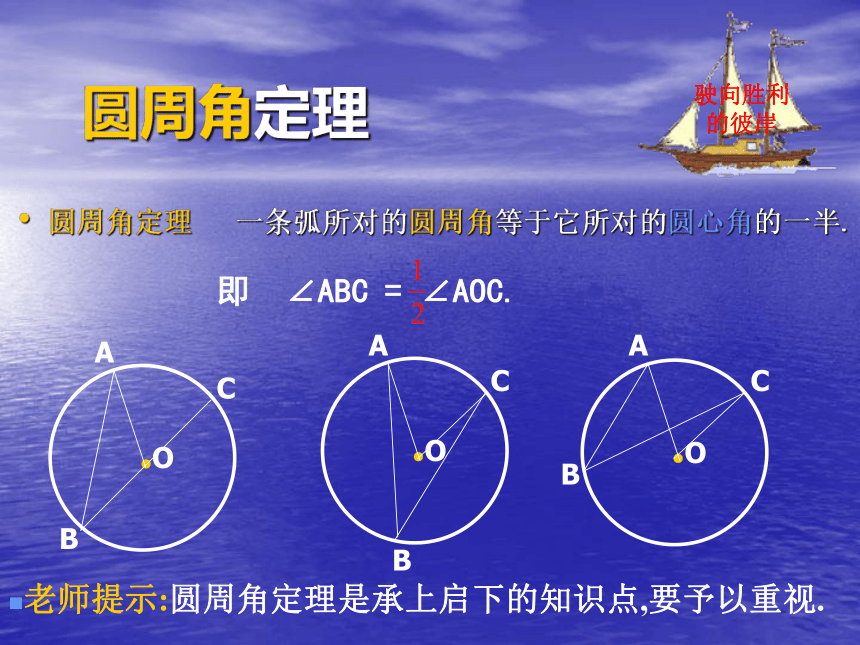
叫圆周角.一、旧知回放:② 角的两边都与圆相交.2、圆心角与所对的弧的关系3、圆周角与所对的弧的关系4、同弧所对的圆心角与圆周角的关系一、旧知回放:圆周角定理圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.驶向胜利的彼岸老师提示:圆周角定理是承上启下的知识点,要予以重视.即 ∠ABC = ∠AOC.1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120o的弧所对的圆周角是60o课前测验B
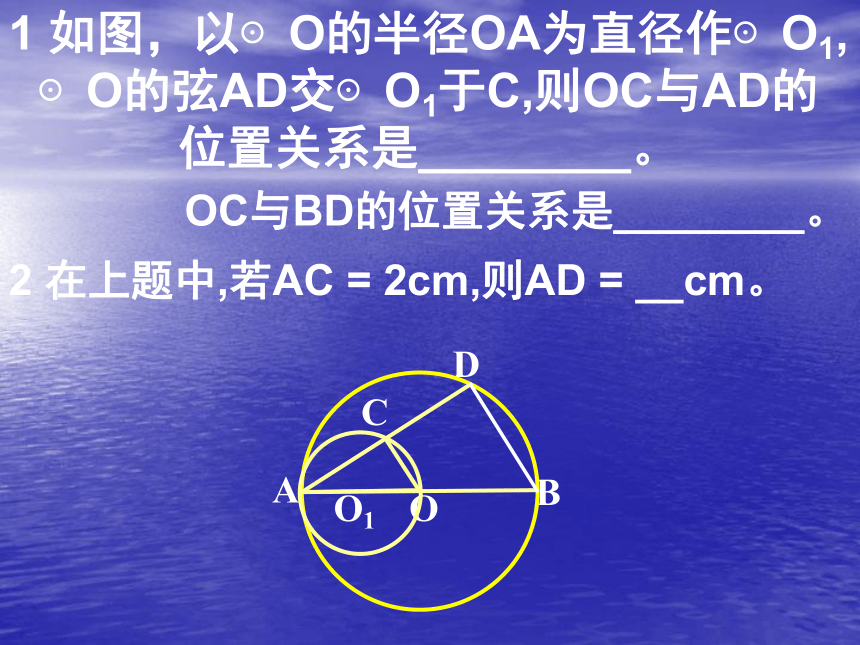
100o50o36o或144o64o100oD1 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则OC与AD的
位置关系是________。2 在上题中,若AC = 2cm,则AD = __cm。OC与BD的位置关系是________。问题讨论问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?图1问题3、如图3,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?∠B = ∠D= ∠E∠BAC =90o问题解答1、圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。2、圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心例1已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒BD=DE证明:连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中,相等的圆周角所对弧相等)。练习:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形证明:∵∠ABC和∠APC
都是⌒所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒ 所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。例题精解例2、如图,AD是△ABC的高,AE是△ABC的外接圆直径。求证:AB · AC = AE · ADAOBCDE分析:要证AB · AC = AE · AD△ADC∽ △ABE或△ACE∽ △ADB题后思:1、证明题的思路寻找方法;
2、等积式的证明方法;
3、辅助线的思考方法。讨论与思考如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE小结与作业1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
3、证明题思路的寻找方法如何?
4、证明等积式的一般思路你掌握了吗?
并且两边都和圆相交的角
叫圆周角.一、旧知回放:② 角的两边都与圆相交.2、圆心角与所对的弧的关系3、圆周角与所对的弧的关系4、同弧所对的圆心角与圆周角的关系一、旧知回放:圆周角定理圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.驶向胜利的彼岸老师提示:圆周角定理是承上启下的知识点,要予以重视.即 ∠ABC = ∠AOC.1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120o的弧所对的圆周角是60o课前测验B
100o50o36o或144o64o100oD1 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则OC与AD的
位置关系是________。2 在上题中,若AC = 2cm,则AD = __cm。OC与BD的位置关系是________。问题讨论问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?图1问题3、如图3,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?∠B = ∠D= ∠E∠BAC =90o问题解答1、圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。2、圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心例1已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒BD=DE证明:连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中,相等的圆周角所对弧相等)。练习:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形证明:∵∠ABC和∠APC
都是⌒所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒ 所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。例题精解例2、如图,AD是△ABC的高,AE是△ABC的外接圆直径。求证:AB · AC = AE · ADAOBCDE分析:要证AB · AC = AE · AD△ADC∽ △ABE或△ACE∽ △ADB题后思:1、证明题的思路寻找方法;
2、等积式的证明方法;
3、辅助线的思考方法。讨论与思考如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE小结与作业1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
3、证明题思路的寻找方法如何?
4、证明等积式的一般思路你掌握了吗?
