2025年九年级中考数学三轮冲刺训练反比例函数中面积相关问题(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练反比例函数中面积相关问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 997.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 05:21:17 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练反比例函数中面积相关问题
1.如图,一次函数y=kx﹣1的图象与反比例函数的图象交于A(a,1),B(﹣2,﹣2)两点.
(1)求一次函数和反比例函数的表达式;
(2)直接写出不等式的解集;
(3)设直线AB与x轴交于点C,若P为x轴上的一动点,连接AP,当△APC的面积为2.5时,求点P的坐标.
2.如图,一次函数y=﹣x+4的图象与反比例函数(k为常数,k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式;
(2)若BE⊥y轴于点E,求△BOE的面积;
(3)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
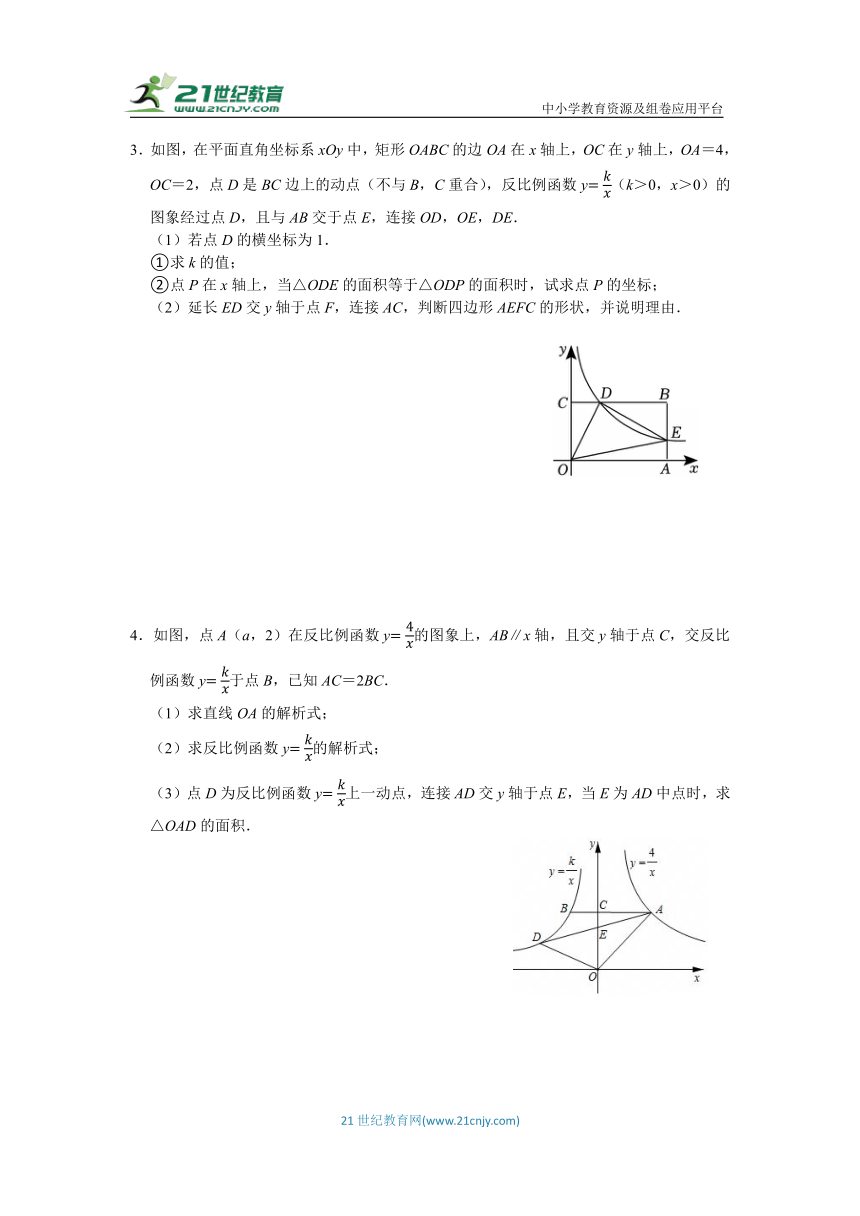
3.如图,在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,OC在y轴上,OA=4,OC=2,点D是BC边上的动点(不与B,C重合),反比例函数y(k>0,x>0)的图象经过点D,且与AB交于点E,连接OD,OE,DE.
(1)若点D的横坐标为1.
①求k的值;
②点P在x轴上,当△ODE的面积等于△ODP的面积时,试求点P的坐标;
(2)延长ED交y轴于点F,连接AC,判断四边形AEFC的形状,并说明理由.
4.如图,点A(a,2)在反比例函数y的图象上,AB∥x轴,且交y轴于点C,交反比例函数y于点B,已知AC=2BC.
(1)求直线OA的解析式;
(2)求反比例函数y的解析式;
(3)点D为反比例函数y上一动点,连接AD交y轴于点E,当E为AD中点时,求△OAD的面积.
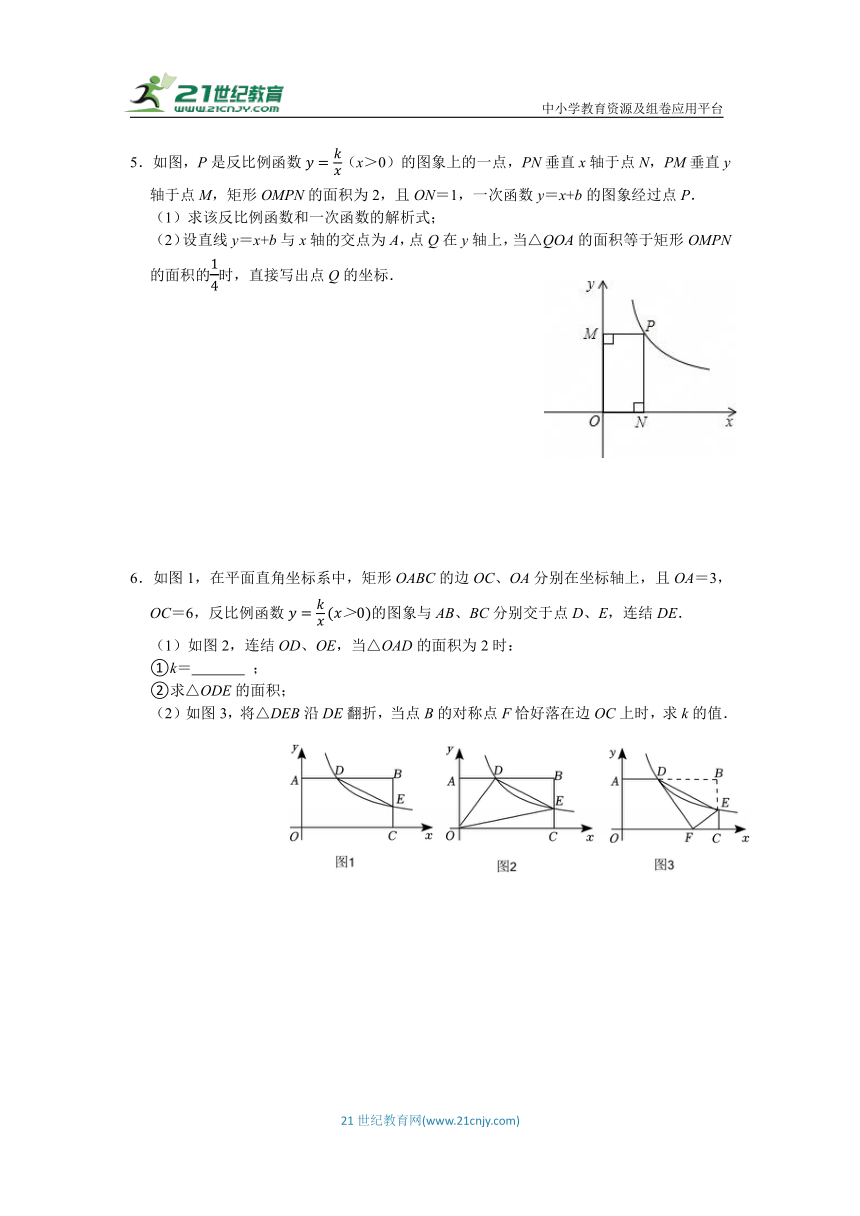
5.如图,P是反比例函数(x>0)的图象上的一点,PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数y=x+b的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线y=x+b与x轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的时,直接写出点Q的坐标.
6.如图1,在平面直角坐标系中,矩形OABC的边OC、OA分别在坐标轴上,且OA=3,OC=6,反比例函数的图象与AB、BC分别交于点D、E,连结DE.
(1)如图2,连结OD、OE,当△OAD的面积为2时:
①k= ;
②求△ODE的面积;
(2)如图3,将△DEB沿DE翻折,当点B的对称点F恰好落在边OC上时,求k的值.
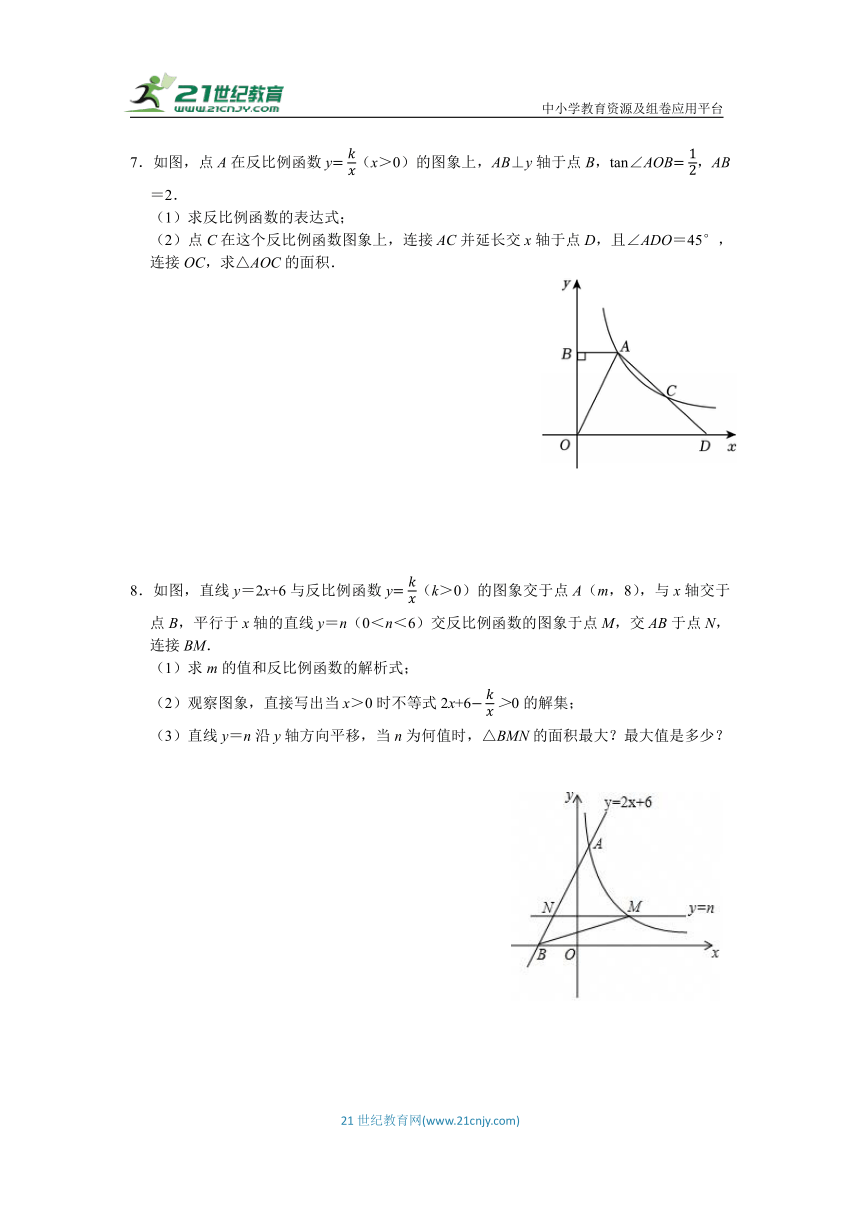
7.如图,点A在反比例函数y(x>0)的图象上,AB⊥y轴于点B,tan∠AOB,AB=2.
(1)求反比例函数的表达式;
(2)点C在这个反比例函数图象上,连接AC并延长交x轴于点D,且∠ADO=45°,连接OC,求△AOC的面积.
8.如图,直线y=2x+6与反比例函数y(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+60的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
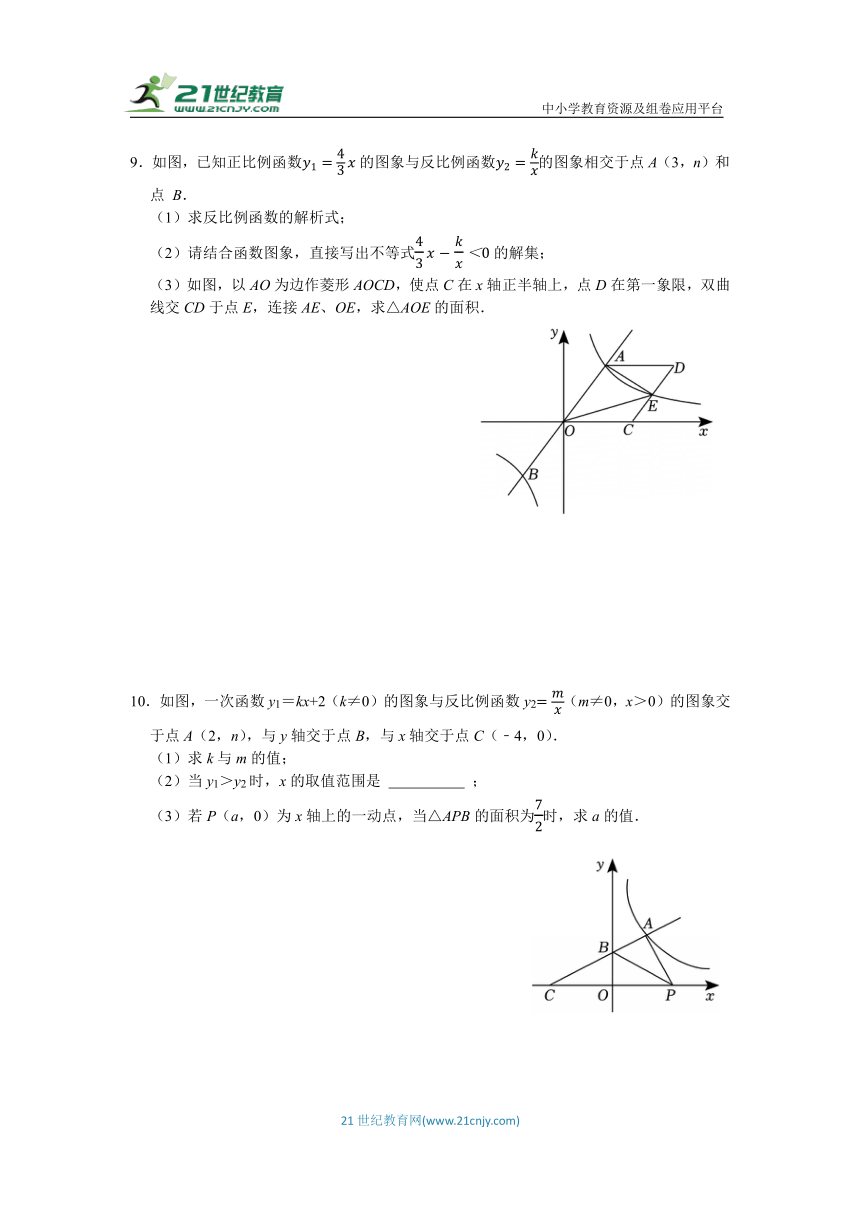
9.如图,已知正比例函数的图象与反比例函数的图象相交于点A(3,n)和点 B.
(1)求反比例函数的解析式;
(2)请结合函数图象,直接写出不等式的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
10.如图,一次函数y1=kx+2(k≠0)的图象与反比例函数y2(m≠0,x>0)的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)当y1>y2时,x的取值范围是 ;
(3)若P(a,0)为x轴上的一动点,当△APB的面积为时,求a的值.
11.如图,一次函数y1=ax+b的图象与反比例函数的图象交于点A(4,m),B(﹣6,﹣2).
(1)求k的值和一次函数的表达式;
(2)关于x的不等式的解集为 ;
(3)若点P为直线AB上的动点,过点P作PQ∥y轴,与反比例函数的图象交于点Q,当△OPQ的面积为6时,请直接写出点Q的坐标.
12.如图,矩形OABC在平面直角坐标系中,反比例函数y(k≠0)分别与边BC、AB交于E、F两点,连接OE、OF,作直线EF分别交y轴、x轴于点G、H.
(1)S△ocE S△OAF(填“>”、“<”、“=”);
(2)若OA=8,OC=4,S△AFH=S△BEF,求k的值;
(3)当,时,求的值.
13.如图,已知反比例函数y的图象与直线y=k2x+b交于点A(4,﹣1),B(m,6),点C是x轴上的一点,连接AC,BC.
(1)求反比例函数的表达式及直线AB的函数表达式;
(2)若S△ABC=21,求点C的坐标;
(3)如图2,直线l绕若点D(2,2)旋转,直线l上有一动点P,过P作PM∥x轴交反比例图象于M,作PN∥y轴交反比例函数图象于N,连接MN,若在直线l上刚好存在三个不同的P点且使得△PMN的面积为9时,求此时直线l的斜率.
14.如图1,反比例函数的图象经过点,射线AB与反比例函数的图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴于点D.
(1)填空:①k的值为 .
②tan∠DAC= ;直线AC的函数解析式为 .
(2)如图2,M是线段AC上方反比例函数图象上一动点,过点M作直线l⊥x轴,与AC交于点N,连接CM.求△CMN面积的最大值.
15.如图,一次函数y2的图象与反比例函数y(k≠0,x>0)的图象相交于点A(2,a),与x轴交于C点,与y轴交于B点.
(1)由图象可知,当x 时,;
(2)求出a,k的值;
(3)若M(m,0)为x轴上的一动点,当△AMB的面积为时,求m的值;
(4)在x轴上是否存在点D,使得∠BOA=∠OAD,若存在,请直接写出点D坐标,若不存在,请说明理由.
参考答案
1.【解答】解:(1)∵图象经过B(﹣2,﹣2),
∴m=4,
∴反比例函数表达式为:;
将A(a,1)代入得,
解得:a=4,
∴A(4,1),
将B(﹣2,﹣2)代入y=kx﹣1,
得﹣2=﹣2k﹣1,
解得:,
∴;
(2)由图可得,不等式的解集是x<﹣2或0<x<4;
(3)解:直线AB与x轴交于点C,
当y=0时,0,
解得:x=2,
∴C(2,0),
设P(t,0),
∴PC=|2﹣t|,
∵△APC的面积为2.5,
∴,
∴2﹣t=±5,
解得:t=﹣3或t=7,
∴点P的坐标为(7,0)或(﹣3,0).
2.【解答】解:(1)∵点A(1,a)在一次函数y=﹣x+4的图象上,
∴a=﹣1+4=3,
∴点A的坐标为(1,3).
∵点A(1,3)在反比例函数数(k为常数,k≠0)的图象上,
∴k=1×3=3,
∴反比例函数的表达式为y;
(2)∵BE⊥y轴于点E,
∴△BOE的面积|k|;
(3)联立直线AB与反比例函数的表达式,得:,
解得或,
∴点B的坐标为(3,1),
作点A关于x轴的轴对点A′,连接A′B交x轴于P,此时,PA+PB的值最小,
∵点A的坐标为(1,3),
∴点A′的坐标为(1,﹣3),
设直线A′B的解析式为y=kx+b,
∴,
∴,
∴直线A′B的解析式为y=x﹣4,
当y=0时,x=4,
∴P(4,0).
3.【解答】解:(1)①∵四边形ABCO是矩形,
∴∠BCO=∠B=∠AOC=90°,
∵OC=2,点D的横坐标为1,
∴D(1,2),
∵反比例函数y(k>0,x>0)的图象经过点D,
∴k=1×2=2;
②∵OC=2,D(1,2),
∴CD=1,
∵D,E都在反比例函数y的图象上,
∴S△COD=S△AOE=1,
∵OA=4,
∴AE,
∴S△ODE=2×4﹣1﹣13,
∵点P在x轴上,
∴设P(x,0),
∴S△ODP,
解得:x=±,
∴P(,0)或(,0);
(2)连接AC,四边形AEFC是平行四边形,理由如下:
由题意得:D(,2),E(4,),
设EF的函数解析式为:y=ax+b,
则,
解得,
∴OF,
∴CF=OF﹣2AE,
又∵CF∥AE,
∴四边形AEFC是平行四边形.
4.【解答】解:(1)∵点A(a,2)在反比例函数y的图象上,
∴2,解得a=2,
∴A(2,2),
设直线OA解析式为y=mx,
则2=2m,解得m=1,
∴直线OA解析式为y=x;
(2)由(1)知:A(2,2),
∵AB∥x轴,且交y轴于点C,
∴AC=2,
∵AC=2BC,
∴BC=1,
∴B(﹣1,2),
把B(﹣1,2)代入y得:2,
∴k=﹣2,
∴反比例函数y的解析式为y;
(3)设D(t,),而A(2,2),
∴AD中点E(,1),
而E在y轴上,
∴0,解得t=﹣2,
∴D(﹣2,1),E(0,),
∴S△DOEOE |xD|2,
S△AOEOE |xA|2,
∴△OAD面积S=S△DOE+S△AOE=3.
5.【解答】解:(1)∵PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,
∴PN=2、
∴点P的坐标为(1,2).
∵反比例函数(x>0)的图象、一次函数y=x+b的图象都经过点P,
由,2=1+b得k=2,b=1、
∴反比例函数为,一次函数为y=x+1;
(2)Q1(0,1),Q2(0,﹣1).
6.【解答】解:(1)①∵△OAD的面积=2,
即,
∴k=4,
故答案为:4;
②在矩形OABC中,OA=BC=3,OC=AB=6,
∵k=4,
∴反比例函数的解析式是:y(x>0),
∵OA=3,
即点D的纵坐标是3,
令y3,
解得:x,
∴D(,3),
同理,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
∴S△ODE=S矩形OABC﹣S△OAD﹣S△OCE﹣S△BDE=OA OC;
(2)过点D作DG⊥x轴于点G,则DG=OA=3,
∵OA=3,即点D的纵坐标是3,
令y,
得:x,
∴D(,3),
同理可得,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
由折叠的性质可知:DF=BD=6,FE=BE=3,∠DFE=∠B=90°,
∴∠DFG+∠CFE=90°,
∵DG⊥x轴,
∴∠DFG+∠GDF=90°,
∴∠CFE=∠GDF,
∵∠CFE=∠GDF,∠FCE=∠DGF=90°,
∴△CFE∽△GDF,
∴,
即,
∴GF,
∵DG⊥x轴,
∴△GDF是直角三角形,DG2+GF2=DF2,
∴,
解得:k,
即k的值为.
7.【解答】解:(1)∵AB⊥y轴于点B,
∴∠OBA=90°,
在Rt△OBA中,AB=2,tan∠AOB,
∴OB=4,
∴A(2,4),
∵点A在反比例函数y(x>0)的图象上,
∴k=4×2=8;
∴反比例函数的解析式为y;
(2)如图,过A作AF⊥x轴于F,过C作CE⊥x轴于E,
∴∠AFD=90°,
∵∠ADO=45°,
∴∠FAD=90°﹣∠CDE=45°,
∴AF=DF=OB=4,
∵OF=AB=2,
∴OD=6,
∴D(6,0),
设直线AC的解析式为y=ax+b,
∵点A(2,4),D(6,0)在直线AC上,
∴,
解得,
∴直线AC的解析式为y=﹣x+6①,
由(1)知,反比例函数的解析式为y②,
联立①②解得,或,
∴C(4,2),
∵△AOF的面积OF AF2×4=4,△OCE的面积OE CE2×4=4,
∴△AOF的面积=△OCE的面积,
∴△AOF的面积﹣△OFH的面积=△OCE的面积﹣△OFH的面积,
∴△AOF的面积=梯形CEFH的面积,
∴△AOC的面积=梯形CEFH的面积(AF+CE) EF(4+2)(4﹣2)=6.
8.【解答】解:(1)∵直线y=2x+6经过点A(m,8),
∴2×m+6=8,
解得m=1,
∴A(1,8),
∴k=2×1+6=8,
∴反比例函数的解析式为y.
(2)不等式2x+60的解集为x>1.
(3)由题意,点M,N的坐标为M(,n),N(,n),
∵0<n<6,
∴0,
∴0
∴S△BMN|MN|×|yM|()×n(n﹣3)2,
∴n=3时,△BMN的面积最大,最大值为.
9.【解答】解:(1)把点A(3,n)代入正比例函数可得:n=4,
∴点A(3,4),
把点A(3,4)代入反比例函数,
可得:k=3×4=12,
∴反比例函数的解析式为;
(2)∵点A与点B是关于原点对称的,
∴点B(﹣3,﹣4),
∴根据图象可得,不等式的解集为:x<﹣3或0<x<3;
(3)如图所示,过点A作AG⊥x轴,垂足为G,
∵A(3,4),
∴OG=3,AG=4,
在Rt△AOG中,,
∵四边形AOCD是菱形,
∴OC=OA=5,,
∴.
10.【解答】解:(1)把C(﹣4,0)代入y=kx+2得:0=﹣4k+2,
解得:k,
把A(2,n)代入y=kx+2得:n=3.
∴A(2,3).
把A(2,3)代入y=得:m=6.
∴k的值为,m的值为6.
(2)由图象可知:当 x>2时,yx+2的图象在y的上方,
∴当y1>y2时,x的取值范围是:x>2.
故答案为:x>2.
(3)当x=0时,yx+2=2.
∴B(0,2),
∵P(a,0)为x轴上的一动点,
∴PC=|a+4|.
∴S△CBPPC OB|a+4|×2=|a+4|,
S△CAPPC yA|a+4|×3|a+4|,
∵S△CAP=S△ABP+S△CBP,
∴|a+4||a+4|,
∴a=3或a=﹣11.
11.【解答】解:(1)将点A、B的坐标代入反比例函数表达式得:k=4m=﹣6×(﹣2)=12,
则k=12,m=3,
即反比例函数的表达式为:y,点A(4,3);
将点A、B的坐标代入一次函数表达式得:
,解得:,
则一次函数表达式为:yx+1;
(2)观察函数图象知,不等式的解集为x>4或﹣6<x<0,
故答案为:x>4或﹣6<x<0;
(3)设点P(x,x+1),则点Q(x,),
则△OPQ的面积PQ×|xP||x+1|×|x|=6,
解得:x=0(舍去)或6或﹣8或﹣2,
即点Q的坐标为:(6,2)或(﹣8,)或(﹣2,﹣6).
12.【解答】解:(1)∵四边形ABCO是矩形,
∴BC⊥y轴,AB⊥x轴,
∵反比例函数y(k≠0)分别与边BC、AB交于E、F两点,
∴S△OCEk,S△OAFk;
∴S△OCE=S△OAF;
故答案为:=;
(2)∵四边形ABCO是矩形,
∴∠B=∠BCO=∠BAO=90°,AB=OC4,OA=BC=8,
∵∠B=∠FAH=90°,∠BFE=∠AFH,
∴△BFE∽△AFH,
∴()2,
∵S△AFH=S△BEF,
∴1(负值舍去),
∴BF=AF=2,
∴F(8,2),
∴,
∴k=16;
(3)∵时,
∴设CE=m,BE=3m,
∴BC=OA=4m,
∴E(m,),F(4m,),
∴BF,
∵△BFE∽△AFH,
∴,
∴,
∴AH=m,
∴OH=OA+AH=5m,
∴.
13.【解答】解:(1)将点A(4,﹣1)代入y,得﹣1,
∴k1=﹣4,
∴反比例函数的表达式为y,
把B(m,6)代入y,得6,
解得:m,
∴B(,6),
将A、B两点坐标分别代入y=k2x+b,得:,
解得:,
∴直线AB的函数表达式为yx+5;
(2)设C(t,0),直线AB与x轴交于点E,
在yx+5中,令y=0,得x+5=0,
解得:x,
∴E(,0),
则CE=|t|,
∵S△ABC=21,
∴S△ACE+S△BCE=21,
即|t|×(6+1)=21,
解得:t或,
∴点C的坐标为(,0)或(,0);
(3)设直线l的解析式为y=kx+b,把D(2,2)代入得:2=2k+b,
∴b=2﹣2k,
∴y=kx+2﹣2k,
由(1)知:反比例函数的解析式为y,
设P(n,kn+2﹣2k),则N(n,),M(,kn+2﹣2k),
∵S△PMN=9,
∴PM PN=18,
∴|n|×|kn+2﹣2k|=18,
整理得:18,
令n(kn+2﹣2k)=m,
则(m+4)2=18|m|,
当m>0时,则(m+4)2=18m,
即m2﹣10m+16=0,
解得:m=2或m=8,
∴n(kn+2﹣2k)=2或n(kn+2﹣2k)=8,即kn2+(2﹣2k)n﹣2=0①或kn2+(2﹣2k)n﹣8=0②,
在方程①中,Δ=(2﹣2k)2+8k=4k2+4>0,该方程中n有两个不同的解,
∵在直线l上刚好存在三个不同的P点,即n有3个不同的解,
∴n还有一个解必定在方程②中,
∴Δ=(2﹣2k)2+32k=4(k2+6k+1)=0,
解得:k=﹣3﹣2或k=﹣3+2;
当m<0时,则(m+4)2=﹣18m,
即m2+26m+16=0,
解得:m=﹣13+3或m=﹣13﹣3,
∴kn2+(2﹣2k)n+13﹣30③或kn2+(2﹣2k)n+13+30④,
在方程③中,Δ=(2﹣2k)2﹣4(13﹣3)k=4[k2+(315)k+1],
在方程④中,Δ=(2﹣2k)2﹣4(13+3)k=4[k2﹣(315)k+1],
∵在直线l上刚好存在三个不同的P点,即n有3个不同的解,
∴(Ⅰ)或(Ⅱ),
由(Ⅰ)得:k或,
由(Ⅱ)得:无解,
综上所述,此时直线l的斜率为k=﹣3﹣2或﹣3+2或或.
14.【解答】解:(1)①∵反比例函数的图象经过点,
∴,
∴.
故答案为:;
②:由①知反比例函数解析式为,
∵射线AB与反比例函数的图象交于另一点B(1,a),将点B的坐标代入得:
a2,
∴,
过B作BE⊥AD于E,如图1,
则.
∴∠ABE=∠BAE=45°,
又∵∠BAC=75°,
∴∠DAC=30°,
∴tan∠DAC=tan30°,
∴DCAD2,
∴OC=2﹣1=1,
∴C(0,﹣1),
设直线AC的解析式为y=kx+b,将点A,点C的坐标代入得:
,
解得,
∴直线AC的解析式为.
故答案为:;;
(2)M是线段AC上方反比例函数图象上一动点,过点M的直线l⊥x轴,设M(m,)(0<m<2),则N(m,),
∴MN,
∴S△CMN m
,
∵0,0<m<2,
∴当时,△CMN的面积有最大值,最大值为.
15.【解答】解:(1)根据图像可以看出表示一次函数在双曲线上方部分,
∴当x>2时,,
故答案为:>2;
(2)由题意可知点A(2,a)在一次函数的图象上,
∴,
∴A(2,3).
∵一次函数的图象与反比例函数的图象相交于点A,
∴,
∴k=6;
(3)一次函数y2的图象与x轴交于C点,与y轴交于B点.
当x=0时,得:y=2,
当y=0时,得:,
解得:x=﹣4,
∴B(0,2),C(﹣4,0).
∵M(m,0)为x轴的一动点,
∴CM=|m|﹣(﹣4)=|m|+4,
∴,
,
∵S△AMB=S△ACM﹣S△BCM,,
∴,
解得:m=3或﹣11;
(4)在x轴上存在点D,使得∠BOA=∠OAD;D的坐标为(2,0)或.理由如下:
过A作AD⊥x轴于D,如图,
∴AD∥y轴,
∴∠AOB=∠OAD,
∵A(2,a),k=6,
∴,
把x=2,代入,
∴D(2,0),
作OA的垂直平分线交y轴于E,交OA于F,连接AE,并延长AE交x轴于D′,
∴△EOA是等腰三角形,
∴∠AOB=∠OAD′,
∵A(2,3),
∴,
∵,
∴,
∴,
设直线AE的解析式为:y=mx+n,
把A(2,3),代入解析式可得:,
解得:,
∴直线AE的解析式为:,
把y=0代入,
解得:,
∴,
综上所述,在x轴上存在点D,使得∠BOA=∠OAD;D的坐标为(2,0)或.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练反比例函数中面积相关问题
1.如图,一次函数y=kx﹣1的图象与反比例函数的图象交于A(a,1),B(﹣2,﹣2)两点.
(1)求一次函数和反比例函数的表达式;
(2)直接写出不等式的解集;
(3)设直线AB与x轴交于点C,若P为x轴上的一动点,连接AP,当△APC的面积为2.5时,求点P的坐标.
2.如图,一次函数y=﹣x+4的图象与反比例函数(k为常数,k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式;
(2)若BE⊥y轴于点E,求△BOE的面积;
(3)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
3.如图,在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,OC在y轴上,OA=4,OC=2,点D是BC边上的动点(不与B,C重合),反比例函数y(k>0,x>0)的图象经过点D,且与AB交于点E,连接OD,OE,DE.
(1)若点D的横坐标为1.
①求k的值;
②点P在x轴上,当△ODE的面积等于△ODP的面积时,试求点P的坐标;
(2)延长ED交y轴于点F,连接AC,判断四边形AEFC的形状,并说明理由.
4.如图,点A(a,2)在反比例函数y的图象上,AB∥x轴,且交y轴于点C,交反比例函数y于点B,已知AC=2BC.
(1)求直线OA的解析式;
(2)求反比例函数y的解析式;
(3)点D为反比例函数y上一动点,连接AD交y轴于点E,当E为AD中点时,求△OAD的面积.
5.如图,P是反比例函数(x>0)的图象上的一点,PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数y=x+b的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线y=x+b与x轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的时,直接写出点Q的坐标.
6.如图1,在平面直角坐标系中,矩形OABC的边OC、OA分别在坐标轴上,且OA=3,OC=6,反比例函数的图象与AB、BC分别交于点D、E,连结DE.
(1)如图2,连结OD、OE,当△OAD的面积为2时:
①k= ;
②求△ODE的面积;
(2)如图3,将△DEB沿DE翻折,当点B的对称点F恰好落在边OC上时,求k的值.
7.如图,点A在反比例函数y(x>0)的图象上,AB⊥y轴于点B,tan∠AOB,AB=2.
(1)求反比例函数的表达式;
(2)点C在这个反比例函数图象上,连接AC并延长交x轴于点D,且∠ADO=45°,连接OC,求△AOC的面积.
8.如图,直线y=2x+6与反比例函数y(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+60的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
9.如图,已知正比例函数的图象与反比例函数的图象相交于点A(3,n)和点 B.
(1)求反比例函数的解析式;
(2)请结合函数图象,直接写出不等式的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
10.如图,一次函数y1=kx+2(k≠0)的图象与反比例函数y2(m≠0,x>0)的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)当y1>y2时,x的取值范围是 ;
(3)若P(a,0)为x轴上的一动点,当△APB的面积为时,求a的值.
11.如图,一次函数y1=ax+b的图象与反比例函数的图象交于点A(4,m),B(﹣6,﹣2).
(1)求k的值和一次函数的表达式;
(2)关于x的不等式的解集为 ;
(3)若点P为直线AB上的动点,过点P作PQ∥y轴,与反比例函数的图象交于点Q,当△OPQ的面积为6时,请直接写出点Q的坐标.
12.如图,矩形OABC在平面直角坐标系中,反比例函数y(k≠0)分别与边BC、AB交于E、F两点,连接OE、OF,作直线EF分别交y轴、x轴于点G、H.
(1)S△ocE S△OAF(填“>”、“<”、“=”);
(2)若OA=8,OC=4,S△AFH=S△BEF,求k的值;
(3)当,时,求的值.
13.如图,已知反比例函数y的图象与直线y=k2x+b交于点A(4,﹣1),B(m,6),点C是x轴上的一点,连接AC,BC.
(1)求反比例函数的表达式及直线AB的函数表达式;
(2)若S△ABC=21,求点C的坐标;
(3)如图2,直线l绕若点D(2,2)旋转,直线l上有一动点P,过P作PM∥x轴交反比例图象于M,作PN∥y轴交反比例函数图象于N,连接MN,若在直线l上刚好存在三个不同的P点且使得△PMN的面积为9时,求此时直线l的斜率.
14.如图1,反比例函数的图象经过点,射线AB与反比例函数的图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴于点D.
(1)填空:①k的值为 .
②tan∠DAC= ;直线AC的函数解析式为 .
(2)如图2,M是线段AC上方反比例函数图象上一动点,过点M作直线l⊥x轴,与AC交于点N,连接CM.求△CMN面积的最大值.
15.如图,一次函数y2的图象与反比例函数y(k≠0,x>0)的图象相交于点A(2,a),与x轴交于C点,与y轴交于B点.
(1)由图象可知,当x 时,;
(2)求出a,k的值;
(3)若M(m,0)为x轴上的一动点,当△AMB的面积为时,求m的值;
(4)在x轴上是否存在点D,使得∠BOA=∠OAD,若存在,请直接写出点D坐标,若不存在,请说明理由.
参考答案
1.【解答】解:(1)∵图象经过B(﹣2,﹣2),
∴m=4,
∴反比例函数表达式为:;
将A(a,1)代入得,
解得:a=4,
∴A(4,1),
将B(﹣2,﹣2)代入y=kx﹣1,
得﹣2=﹣2k﹣1,
解得:,
∴;
(2)由图可得,不等式的解集是x<﹣2或0<x<4;
(3)解:直线AB与x轴交于点C,
当y=0时,0,
解得:x=2,
∴C(2,0),
设P(t,0),
∴PC=|2﹣t|,
∵△APC的面积为2.5,
∴,
∴2﹣t=±5,
解得:t=﹣3或t=7,
∴点P的坐标为(7,0)或(﹣3,0).
2.【解答】解:(1)∵点A(1,a)在一次函数y=﹣x+4的图象上,
∴a=﹣1+4=3,
∴点A的坐标为(1,3).
∵点A(1,3)在反比例函数数(k为常数,k≠0)的图象上,
∴k=1×3=3,
∴反比例函数的表达式为y;
(2)∵BE⊥y轴于点E,
∴△BOE的面积|k|;
(3)联立直线AB与反比例函数的表达式,得:,
解得或,
∴点B的坐标为(3,1),
作点A关于x轴的轴对点A′,连接A′B交x轴于P,此时,PA+PB的值最小,
∵点A的坐标为(1,3),
∴点A′的坐标为(1,﹣3),
设直线A′B的解析式为y=kx+b,
∴,
∴,
∴直线A′B的解析式为y=x﹣4,
当y=0时,x=4,
∴P(4,0).
3.【解答】解:(1)①∵四边形ABCO是矩形,
∴∠BCO=∠B=∠AOC=90°,
∵OC=2,点D的横坐标为1,
∴D(1,2),
∵反比例函数y(k>0,x>0)的图象经过点D,
∴k=1×2=2;
②∵OC=2,D(1,2),
∴CD=1,
∵D,E都在反比例函数y的图象上,
∴S△COD=S△AOE=1,
∵OA=4,
∴AE,
∴S△ODE=2×4﹣1﹣13,
∵点P在x轴上,
∴设P(x,0),
∴S△ODP,
解得:x=±,
∴P(,0)或(,0);
(2)连接AC,四边形AEFC是平行四边形,理由如下:
由题意得:D(,2),E(4,),
设EF的函数解析式为:y=ax+b,
则,
解得,
∴OF,
∴CF=OF﹣2AE,
又∵CF∥AE,
∴四边形AEFC是平行四边形.
4.【解答】解:(1)∵点A(a,2)在反比例函数y的图象上,
∴2,解得a=2,
∴A(2,2),
设直线OA解析式为y=mx,
则2=2m,解得m=1,
∴直线OA解析式为y=x;
(2)由(1)知:A(2,2),
∵AB∥x轴,且交y轴于点C,
∴AC=2,
∵AC=2BC,
∴BC=1,
∴B(﹣1,2),
把B(﹣1,2)代入y得:2,
∴k=﹣2,
∴反比例函数y的解析式为y;
(3)设D(t,),而A(2,2),
∴AD中点E(,1),
而E在y轴上,
∴0,解得t=﹣2,
∴D(﹣2,1),E(0,),
∴S△DOEOE |xD|2,
S△AOEOE |xA|2,
∴△OAD面积S=S△DOE+S△AOE=3.
5.【解答】解:(1)∵PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,
∴PN=2、
∴点P的坐标为(1,2).
∵反比例函数(x>0)的图象、一次函数y=x+b的图象都经过点P,
由,2=1+b得k=2,b=1、
∴反比例函数为,一次函数为y=x+1;
(2)Q1(0,1),Q2(0,﹣1).
6.【解答】解:(1)①∵△OAD的面积=2,
即,
∴k=4,
故答案为:4;
②在矩形OABC中,OA=BC=3,OC=AB=6,
∵k=4,
∴反比例函数的解析式是:y(x>0),
∵OA=3,
即点D的纵坐标是3,
令y3,
解得:x,
∴D(,3),
同理,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
∴S△ODE=S矩形OABC﹣S△OAD﹣S△OCE﹣S△BDE=OA OC;
(2)过点D作DG⊥x轴于点G,则DG=OA=3,
∵OA=3,即点D的纵坐标是3,
令y,
得:x,
∴D(,3),
同理可得,当x=6时,y,
∴E(6,),
∴AD,BD=AB﹣AD=6,CE,BE=BC﹣CE=3,
由折叠的性质可知:DF=BD=6,FE=BE=3,∠DFE=∠B=90°,
∴∠DFG+∠CFE=90°,
∵DG⊥x轴,
∴∠DFG+∠GDF=90°,
∴∠CFE=∠GDF,
∵∠CFE=∠GDF,∠FCE=∠DGF=90°,
∴△CFE∽△GDF,
∴,
即,
∴GF,
∵DG⊥x轴,
∴△GDF是直角三角形,DG2+GF2=DF2,
∴,
解得:k,
即k的值为.
7.【解答】解:(1)∵AB⊥y轴于点B,
∴∠OBA=90°,
在Rt△OBA中,AB=2,tan∠AOB,
∴OB=4,
∴A(2,4),
∵点A在反比例函数y(x>0)的图象上,
∴k=4×2=8;
∴反比例函数的解析式为y;
(2)如图,过A作AF⊥x轴于F,过C作CE⊥x轴于E,
∴∠AFD=90°,
∵∠ADO=45°,
∴∠FAD=90°﹣∠CDE=45°,
∴AF=DF=OB=4,
∵OF=AB=2,
∴OD=6,
∴D(6,0),
设直线AC的解析式为y=ax+b,
∵点A(2,4),D(6,0)在直线AC上,
∴,
解得,
∴直线AC的解析式为y=﹣x+6①,
由(1)知,反比例函数的解析式为y②,
联立①②解得,或,
∴C(4,2),
∵△AOF的面积OF AF2×4=4,△OCE的面积OE CE2×4=4,
∴△AOF的面积=△OCE的面积,
∴△AOF的面积﹣△OFH的面积=△OCE的面积﹣△OFH的面积,
∴△AOF的面积=梯形CEFH的面积,
∴△AOC的面积=梯形CEFH的面积(AF+CE) EF(4+2)(4﹣2)=6.
8.【解答】解:(1)∵直线y=2x+6经过点A(m,8),
∴2×m+6=8,
解得m=1,
∴A(1,8),
∴k=2×1+6=8,
∴反比例函数的解析式为y.
(2)不等式2x+60的解集为x>1.
(3)由题意,点M,N的坐标为M(,n),N(,n),
∵0<n<6,
∴0,
∴0
∴S△BMN|MN|×|yM|()×n(n﹣3)2,
∴n=3时,△BMN的面积最大,最大值为.
9.【解答】解:(1)把点A(3,n)代入正比例函数可得:n=4,
∴点A(3,4),
把点A(3,4)代入反比例函数,
可得:k=3×4=12,
∴反比例函数的解析式为;
(2)∵点A与点B是关于原点对称的,
∴点B(﹣3,﹣4),
∴根据图象可得,不等式的解集为:x<﹣3或0<x<3;
(3)如图所示,过点A作AG⊥x轴,垂足为G,
∵A(3,4),
∴OG=3,AG=4,
在Rt△AOG中,,
∵四边形AOCD是菱形,
∴OC=OA=5,,
∴.
10.【解答】解:(1)把C(﹣4,0)代入y=kx+2得:0=﹣4k+2,
解得:k,
把A(2,n)代入y=kx+2得:n=3.
∴A(2,3).
把A(2,3)代入y=得:m=6.
∴k的值为,m的值为6.
(2)由图象可知:当 x>2时,yx+2的图象在y的上方,
∴当y1>y2时,x的取值范围是:x>2.
故答案为:x>2.
(3)当x=0时,yx+2=2.
∴B(0,2),
∵P(a,0)为x轴上的一动点,
∴PC=|a+4|.
∴S△CBPPC OB|a+4|×2=|a+4|,
S△CAPPC yA|a+4|×3|a+4|,
∵S△CAP=S△ABP+S△CBP,
∴|a+4||a+4|,
∴a=3或a=﹣11.
11.【解答】解:(1)将点A、B的坐标代入反比例函数表达式得:k=4m=﹣6×(﹣2)=12,
则k=12,m=3,
即反比例函数的表达式为:y,点A(4,3);
将点A、B的坐标代入一次函数表达式得:
,解得:,
则一次函数表达式为:yx+1;
(2)观察函数图象知,不等式的解集为x>4或﹣6<x<0,
故答案为:x>4或﹣6<x<0;
(3)设点P(x,x+1),则点Q(x,),
则△OPQ的面积PQ×|xP||x+1|×|x|=6,
解得:x=0(舍去)或6或﹣8或﹣2,
即点Q的坐标为:(6,2)或(﹣8,)或(﹣2,﹣6).
12.【解答】解:(1)∵四边形ABCO是矩形,
∴BC⊥y轴,AB⊥x轴,
∵反比例函数y(k≠0)分别与边BC、AB交于E、F两点,
∴S△OCEk,S△OAFk;
∴S△OCE=S△OAF;
故答案为:=;
(2)∵四边形ABCO是矩形,
∴∠B=∠BCO=∠BAO=90°,AB=OC4,OA=BC=8,
∵∠B=∠FAH=90°,∠BFE=∠AFH,
∴△BFE∽△AFH,
∴()2,
∵S△AFH=S△BEF,
∴1(负值舍去),
∴BF=AF=2,
∴F(8,2),
∴,
∴k=16;
(3)∵时,
∴设CE=m,BE=3m,
∴BC=OA=4m,
∴E(m,),F(4m,),
∴BF,
∵△BFE∽△AFH,
∴,
∴,
∴AH=m,
∴OH=OA+AH=5m,
∴.
13.【解答】解:(1)将点A(4,﹣1)代入y,得﹣1,
∴k1=﹣4,
∴反比例函数的表达式为y,
把B(m,6)代入y,得6,
解得:m,
∴B(,6),
将A、B两点坐标分别代入y=k2x+b,得:,
解得:,
∴直线AB的函数表达式为yx+5;
(2)设C(t,0),直线AB与x轴交于点E,
在yx+5中,令y=0,得x+5=0,
解得:x,
∴E(,0),
则CE=|t|,
∵S△ABC=21,
∴S△ACE+S△BCE=21,
即|t|×(6+1)=21,
解得:t或,
∴点C的坐标为(,0)或(,0);
(3)设直线l的解析式为y=kx+b,把D(2,2)代入得:2=2k+b,
∴b=2﹣2k,
∴y=kx+2﹣2k,
由(1)知:反比例函数的解析式为y,
设P(n,kn+2﹣2k),则N(n,),M(,kn+2﹣2k),
∵S△PMN=9,
∴PM PN=18,
∴|n|×|kn+2﹣2k|=18,
整理得:18,
令n(kn+2﹣2k)=m,
则(m+4)2=18|m|,
当m>0时,则(m+4)2=18m,
即m2﹣10m+16=0,
解得:m=2或m=8,
∴n(kn+2﹣2k)=2或n(kn+2﹣2k)=8,即kn2+(2﹣2k)n﹣2=0①或kn2+(2﹣2k)n﹣8=0②,
在方程①中,Δ=(2﹣2k)2+8k=4k2+4>0,该方程中n有两个不同的解,
∵在直线l上刚好存在三个不同的P点,即n有3个不同的解,
∴n还有一个解必定在方程②中,
∴Δ=(2﹣2k)2+32k=4(k2+6k+1)=0,
解得:k=﹣3﹣2或k=﹣3+2;
当m<0时,则(m+4)2=﹣18m,
即m2+26m+16=0,
解得:m=﹣13+3或m=﹣13﹣3,
∴kn2+(2﹣2k)n+13﹣30③或kn2+(2﹣2k)n+13+30④,
在方程③中,Δ=(2﹣2k)2﹣4(13﹣3)k=4[k2+(315)k+1],
在方程④中,Δ=(2﹣2k)2﹣4(13+3)k=4[k2﹣(315)k+1],
∵在直线l上刚好存在三个不同的P点,即n有3个不同的解,
∴(Ⅰ)或(Ⅱ),
由(Ⅰ)得:k或,
由(Ⅱ)得:无解,
综上所述,此时直线l的斜率为k=﹣3﹣2或﹣3+2或或.
14.【解答】解:(1)①∵反比例函数的图象经过点,
∴,
∴.
故答案为:;
②:由①知反比例函数解析式为,
∵射线AB与反比例函数的图象交于另一点B(1,a),将点B的坐标代入得:
a2,
∴,
过B作BE⊥AD于E,如图1,
则.
∴∠ABE=∠BAE=45°,
又∵∠BAC=75°,
∴∠DAC=30°,
∴tan∠DAC=tan30°,
∴DCAD2,
∴OC=2﹣1=1,
∴C(0,﹣1),
设直线AC的解析式为y=kx+b,将点A,点C的坐标代入得:
,
解得,
∴直线AC的解析式为.
故答案为:;;
(2)M是线段AC上方反比例函数图象上一动点,过点M的直线l⊥x轴,设M(m,)(0<m<2),则N(m,),
∴MN,
∴S△CMN m
,
∵0,0<m<2,
∴当时,△CMN的面积有最大值,最大值为.
15.【解答】解:(1)根据图像可以看出表示一次函数在双曲线上方部分,
∴当x>2时,,
故答案为:>2;
(2)由题意可知点A(2,a)在一次函数的图象上,
∴,
∴A(2,3).
∵一次函数的图象与反比例函数的图象相交于点A,
∴,
∴k=6;
(3)一次函数y2的图象与x轴交于C点,与y轴交于B点.
当x=0时,得:y=2,
当y=0时,得:,
解得:x=﹣4,
∴B(0,2),C(﹣4,0).
∵M(m,0)为x轴的一动点,
∴CM=|m|﹣(﹣4)=|m|+4,
∴,
,
∵S△AMB=S△ACM﹣S△BCM,,
∴,
解得:m=3或﹣11;
(4)在x轴上存在点D,使得∠BOA=∠OAD;D的坐标为(2,0)或.理由如下:
过A作AD⊥x轴于D,如图,
∴AD∥y轴,
∴∠AOB=∠OAD,
∵A(2,a),k=6,
∴,
把x=2,代入,
∴D(2,0),
作OA的垂直平分线交y轴于E,交OA于F,连接AE,并延长AE交x轴于D′,
∴△EOA是等腰三角形,
∴∠AOB=∠OAD′,
∵A(2,3),
∴,
∵,
∴,
∴,
设直线AE的解析式为:y=mx+n,
把A(2,3),代入解析式可得:,
解得:,
∴直线AE的解析式为:,
把y=0代入,
解得:,
∴,
综上所述,在x轴上存在点D,使得∠BOA=∠OAD;D的坐标为(2,0)或.
21世纪教育网(www.21cnjy.com)
同课章节目录
