2025年九年级中考数学三轮冲刺训练一次函数与几何相关综合问题(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练一次函数与几何相关综合问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 05:23:42 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练一次函数与几何相关综合问题
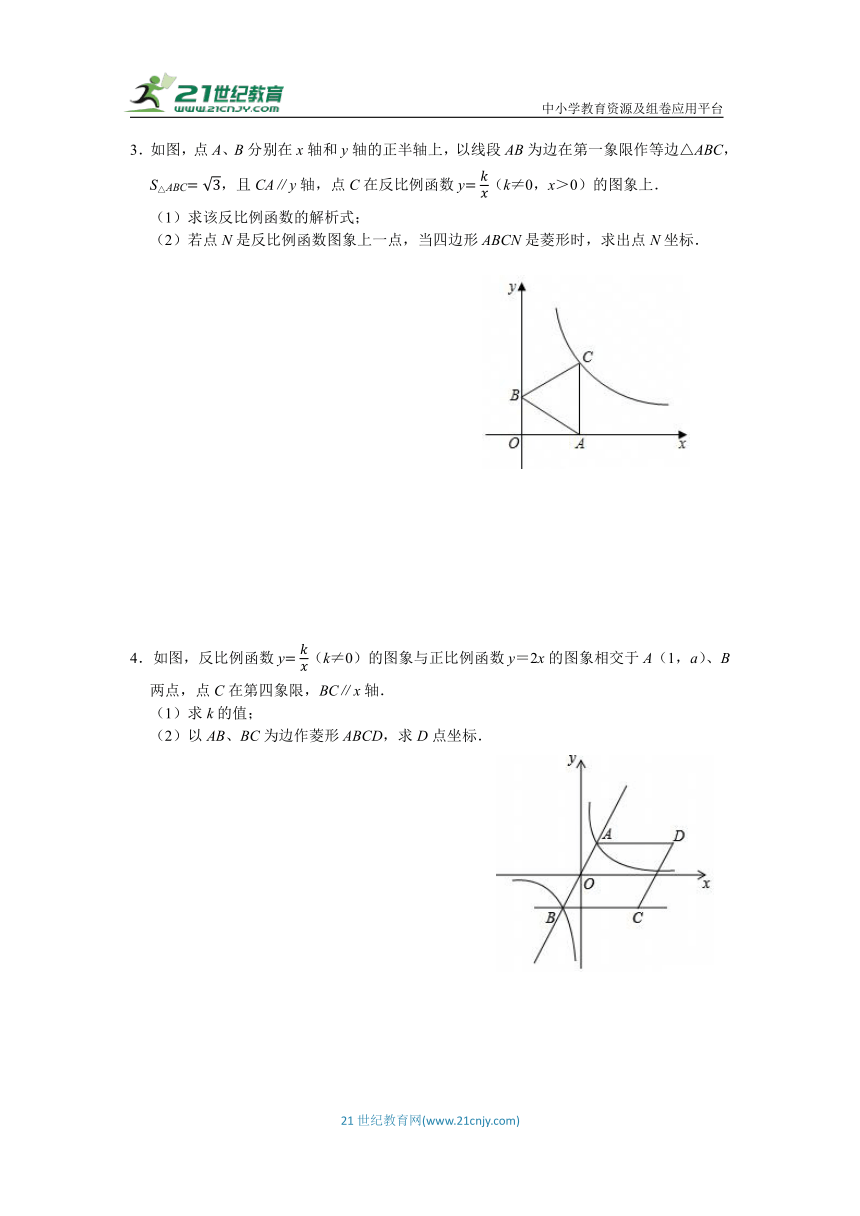
1.如图,直线l1:y=﹣2x+4与x轴交于点B,OB=OC,直线l2:y=kx+b经过点C,且与l1交于点A(1,2).
(1)求直线l2的解析式;
(2)记直线l2与y轴的交点为D,记直线l1与y轴的交点为E,求△ADE的面积;
(3)根据图象,直接写出0≤﹣2x+4<kx+b的解集.
2.如图1,在平面直角坐标系中,直线AB与x轴交于点A(m,0),与y轴交于点B(0,n),且m,n满足:(m+n)2+|n﹣6|=0.
(1)求△AOB的面积;
(2)C为OA延长线上一动点,以BC为直角边作等腰直角△BCE,连接EA,求直线EA与y轴交点F的坐标;
(3)在(2)的条件下,当AC=4时,在坐标平面内是否存在一点P,使以B,E,F,P为顶点的四边形是平行四边形,如果存在,直接写出点P的坐标,若不存在,说明理由.
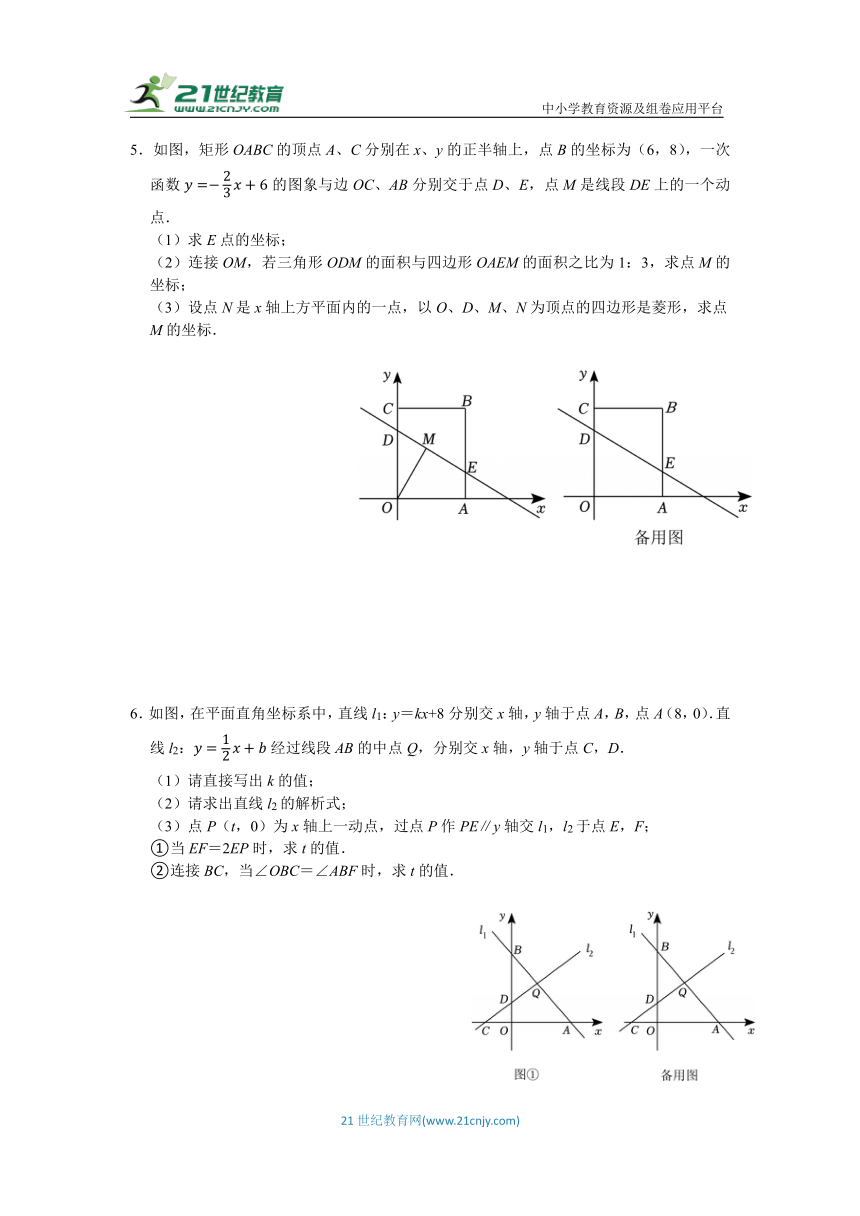
3.如图,点A、B分别在x轴和y轴的正半轴上,以线段AB为边在第一象限作等边△ABC,S△ABC,且CA∥y轴,点C在反比例函数y(k≠0,x>0)的图象上.
(1)求该反比例函数的解析式;
(2)若点N是反比例函数图象上一点,当四边形ABCN是菱形时,求出点N坐标.
4.如图,反比例函数y(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a)、B两点,点C在第四象限,BC∥x轴.
(1)求k的值;
(2)以AB、BC为边作菱形ABCD,求D点坐标.
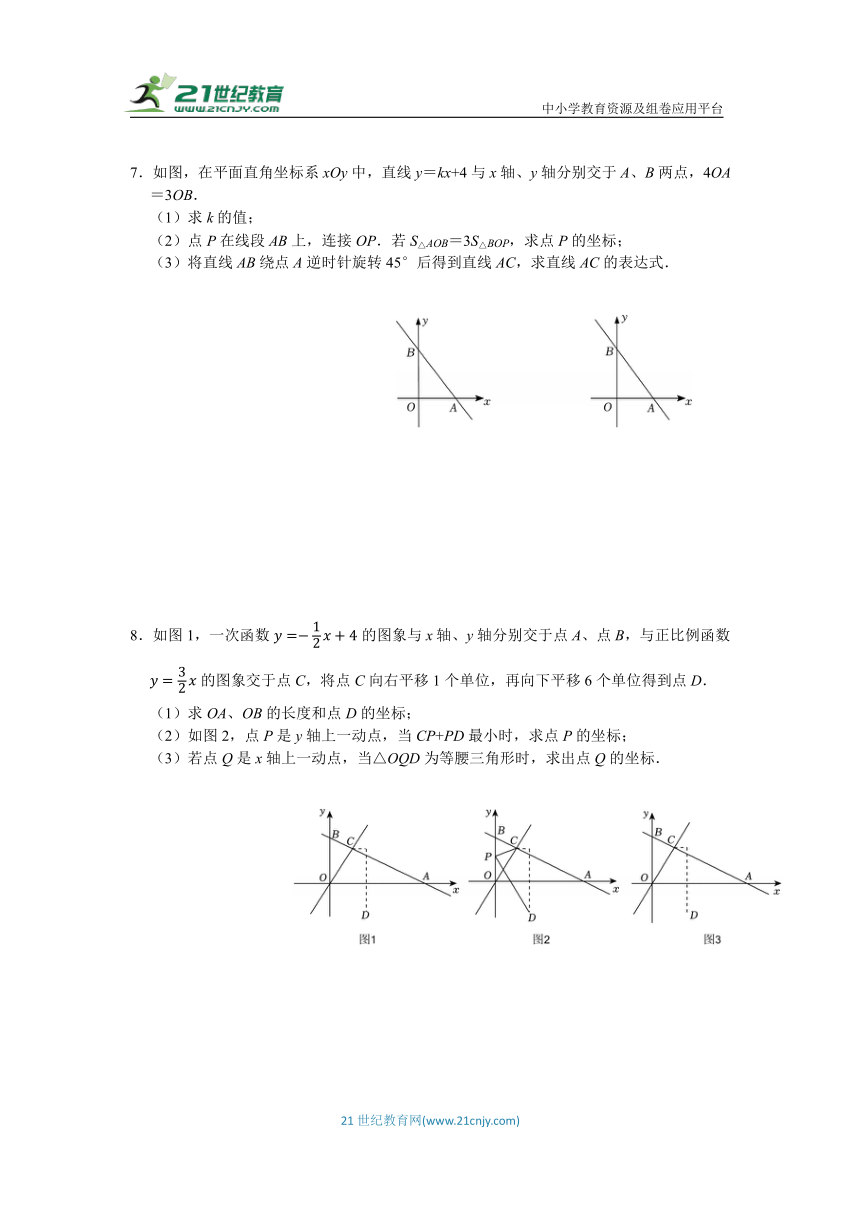
5.如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(6,8),一次函数的图象与边OC、AB分别交于点D、E,点M是线段DE上的一个动点.
(1)求E点的坐标;
(2)连接OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点M的坐标.
6.如图,在平面直角坐标系中,直线l1:y=kx+8分别交x轴,y轴于点A,B,点A(8,0).直线l2:经过线段AB的中点Q,分别交x轴,y轴于点C,D.
(1)请直接写出k的值;
(2)请求出直线l2的解析式;
(3)点P(t,0)为x轴上一动点,过点P作PE∥y轴交l1,l2于点E,F;
①当EF=2EP时,求t的值.
②连接BC,当∠OBC=∠ABF时,求t的值.
7.如图,在平面直角坐标系xOy中,直线y=kx+4与x轴、y轴分别交于A、B两点,4OA=3OB.
(1)求k的值;
(2)点P在线段AB上,连接OP.若S△AOB=3S△BOP,求点P的坐标;
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,求直线AC的表达式.
8.如图1,一次函数的图象与x轴、y轴分别交于点A、点B,与正比例函数的图象交于点C,将点C向右平移1个单位,再向下平移6个单位得到点D.
(1)求OA、OB的长度和点D的坐标;
(2)如图2,点P是y轴上一动点,当CP+PD最小时,求点P的坐标;
(3)若点Q是x轴上一动点,当△OQD为等腰三角形时,求出点Q的坐标.
9.如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(8,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
(1)当b=6时,
①求直线AB的解析式;②若QO=QA,求P点的坐标.
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
10.如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点A的坐标是(0,4),点B的坐标是(8,0).
(1)求对角线AB所在直线的函数关系式;
(2)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;
(3)在(2)的条件下,若点P是直线AB上的一个动点,当△PAM的面积与长方形AOBC的面积相等时,求点P的坐标.
11.如图,已知直线l:y=kx+b与x轴交于A(﹣3,0)、与y轴交于B点,且经过(1,8),在y轴上有一点C(0,3),动点D从点A以每秒1个单位的速度沿x轴向右移动,设动点D的移动时间为t秒.
(1)求k、b的值;
(2)当t为何值时△COD≌△AOB,并求此时点D的坐标;
(3)求△COD的面积S与动点D的移动时间t之间的函数关系式.
12.如图,已知直线y=kx+b经过点A(0,5),B(4,1),并与x轴交于点C,与直线y=2x﹣1相交于点D.
(1)求直线AB的函数表达式;
(2)求不等式kx+b>0的解集;
(3)直线y=2x﹣1与y轴交于点E,在直线AB上是否存在点P,使得S△AED=2S△AEP,若存在,直接写出点P的坐标,若不存在,说明理由.
13.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的?若存在求出此时点M的坐标;若不存在,说明理由.
14.如图1,已知点A和点B坐标分别为(1,0)和(0,3),将线段AB绕点A顺时针旋转90°得到线段AC,连接BC交x轴于点D.
(1)求直线BD的函数关系式;
(2)如图2,若点P为线段BD上一点,且△ABP的面积为,求点P的坐标;
(3)若直线y=﹣x+m与△ABC有公共点,直接写出m的取值范围.
15.如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)求△ADC的面积;
(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.
16.在平面直角坐标系中,一次函数的图象l1与x轴、y轴分别交于点A、B,一次函数的图象l2与x轴、y轴分别交于点C、D.
(1)填空:点A的坐标为 (3,0) ,点B的坐标为 (0,﹣4) ;
(2)在x轴上是否存在点P,使得2∠BPO+∠OBA=90°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)点Q为平面内一点,且△CDQ为等腰直角三角形,请直接写出所有满足条件的点Q的坐标.
参考答案
1.【解答】解:(1)∵l1的直线解析式为y=﹣2x+4,
当y=0时,x=2,
∴B(2,0),
∵OB=OC,
∴C(﹣2,0),
∵l2:y=kx+b经过点C和点A,
,
解得,
∴l2的直线解析式为;
(2)在直线l1的解析式y=﹣2x+4中,
当x=0时,y=4,
∴E(0,4),
在直线l2的解析式中,当x=0时,,
∴,
∴,
∴;
(3)由函数图象可知,0≤﹣2x+4<kx+b的解集为1<x≤2.
2.【解答】解:(1)∵(m+n)2+|n﹣6|=0,
∴n﹣6=0且m+n=0,
解得:,
即点A、B的坐标分别为(﹣6,0)、(0,6),则OA=OB=6,
∴S△AOBOA×OB6×6=18;
(2)如图所示,过点E作EG⊥x轴于G.
∵△ECB为等腰直角三角形,
∴CE=CB,∠ECB=90°,
∴∠ECG+∠OCB=180°﹣90°=90°,
∵EG⊥GC,
∴Rt△EGC中,∠GEC+∠ECG=180°﹣∠EGC=180°﹣90°=90°,
∴∠GEC=∠OCB,
在△ECG和△CBO中:
,
∴△ECG≌△CBO(AAS),
∴CG=BO=6,EG=OC,
设AC=a,
∴OC=OA+AC=6+a=EG,
∴OG=OC+CG=6+a+6=12+a,
∴E点的坐标为(﹣12﹣a,6+a),
∵A(﹣6,0),
由点A、E的坐标得,EA的解析式为y=﹣x﹣6,
∴当x=0时,y=﹣6,
∴EA与y轴的交点坐标为(0,﹣6),
即点F(0,﹣6);
(3)存在,点P的坐标为 (16,﹣10),(﹣16,22),(﹣16,﹣2).
∵AD=a=4,E(﹣12﹣a,6+a),
∴E(﹣16,10),
又∵以B、E、F、P为顶点的四边形是平行四边形,且F(0,﹣6),B(0,6),
设P(a,b),
当BF为对角线时,得:
,
解得:,
∴P(16,﹣10);
当BE为对角线时,得:
,
解得:,
∴P(﹣16,22),
当EF为对角线时,得:
,
解得:,
∴P(﹣16,﹣2)综上所述,点P的坐标为 (16,﹣10),(﹣16,22),(﹣16,﹣2).
3.【解答】解:(1)根据题意,设C点的坐标为(a,b),
∴b,
∴ab=k,即得AC OA=k,
又∵CA∥y轴,
∴S△ABCAC OA,
∴k,
即k=2,
∴反比例函数的解析式为y;
(2)如图,根据菱形的性质可知,AC⊥BN,且AC与BN互相平分,
设菱形对角线的交点为P,设C点坐标为(a,b),
∵△ABC是等边三角形,四边形ABCN是菱形,
∴P(a,b),N(2a,b),
即BP=OA=a,AP=CPb,
∵∠BAC=60°,
∴BP=AP×tan60°,
即ab,
由(1)知ab=2,C点在第一象限,
∴a,b=2,
∴N(2,1).
4.【解答】解:(1)∵点A(1,a)在直线y=2x上,
∴a=2×1=2,
即点A的坐标为(1,2),
∵点A(1,2)是反比例函数y(k≠0)的图象与正比例函数y=2x图象的交点,
∴k=1×2=2,
即k的值是2;
(2)由题意得:2x,
解得:x=1或﹣1,
经检验x=1或﹣1是原方程的解,
∴B(﹣1,﹣2),
∵点A(1,2),
∴AB2,
∵菱形ABCD是以AB、BC为边,且BC∥x轴,
∴AD=AB=2,
∴D(1+2,2).
5.【解答】解:(1)一次函数中,
令x=0,得y=6,
∴D的坐标是(0,6),OD=6,
∵OD=BE,
∴BE=6,
∴E的坐标是(6,2);
(2)S四边形OAED(OD+AE) OA(6+2)×6=24,
∵三角形ODM的面积与四边形OAEM的面积之比为1:3,
∴S△ODM=6.
设M的横坐标是a,则6a=6,
解得:a=2,
把x=a=2代入得:
,
∴M的坐标;
故点M的坐标为;
(3)当四边形OMDN是菱形时,如图(1),
此时,M的纵坐标是3,把y=3代入中,
解得:,
∴M的坐标是;
当四边形OMND是菱形时,如图(2),
∵OM=OD=6,则设M的横坐标是m,则纵坐标是,
∴,
解得:或0(舍去),
∴M的坐标是,
综上,点M的坐标为或.
6.【解答】解:(1)∵A(8,0)过直线l1:y=kx+8,
∴0=k×8+8,
解得:k=﹣1,
∴k=﹣1;
(2)∵l1:y=﹣x+8分别交x轴,y轴于点A,B,
∴B(0,8),
∵AB的中点Q,A(8,0),
∴Q()即Q(4,4),
∵l2:yx+b过Q点,
∴44+b,
解得:b=2,
∴l2:yx+2;
(3)∵P(t,0)为x轴上一动点,过点P作PE∥y轴交l1:y=﹣x+8,l2:yx+2于点E,F;
∴E(t,﹣t+8),F(t,t+2),
t=20,或t;
②∵P(t,0)为x轴上一动点,过点P作PE∥y轴交l1:y=﹣x+8,l2:yx+2于点E,F;
∴E(t,﹣t+8),F(t,t+2),
∵A(8,0),B(0,8),
∴OA=OB=8,
∵∠AOB=90°,
∴∠ABO=45°,ABAO=8,
∵l2:yx+2交x轴于C点,
∴C(﹣4,0),
∵B(0,8),
∴OB=2CO,
当∠OBC=∠ABF时,分两种情况:
F在l1上方时,如图:
过A作AM⊥AB交AF延长线于M点,
∴∠BAM=90°,
∴∠MAN=45°,
作MN⊥x轴于N点,则△AMN是等要直角三角形,
∴AN=MN,
∴∠BAM=∠AOB=90°,∠OBC=∠ABF,
∴△BOC∽△BAM,
∴,即,
解得:AM=4,
∴AN=MN=4,
∴AN=OA+AN=8+4=12,
∴N(12,0),M(12,4),
由B(0,8),
设直线BM:y=nx+8,
∴4=12n+8,
解得:n,
∴BM:yx+8,
∵BM:yx+8过点F(t,t+2),
∴t+2t+8,
解得:t=7.2;
F在l1下方时,如图,
若BF交x轴于N点,过N点作NM⊥AB于M点,
同理:∴△BOC∽△BAM,△AMN是等腰直角三角形,
∴,ANAMNM,
∵BM=AB﹣AM=AB﹣MN=8MN,
∴,
解得:MN,
∴AN,
∴ON=AO﹣AN=8,
∴N(,0),
由B(0,8),
设直线BN:y=nx+8,
∴0n+8,
解得:n=﹣3,
∴BN:y=﹣3x+8,
∵BN:y=﹣3x+8过点F(t,t+2),
∴t+2=﹣3t+8,
解得:t,
综上所述:∠OBC=∠ABF时,t=7.2或.
7.【解答】解:(1)直线y=kx+4中,令x=0,则y=4,
∴B(0,4),
∴OB=4,
∵4OA=3OB,
∴OA=3,
由图可知点A在x轴的正半轴,
∴A(3,0),
∴3k+4=0,
∴k.
(2)由(1)知OA=3,OB=4,yx+4,
∴S△AOB OA OB3×4=6,
∵S△AOB=3S△BOP,
∴S△BOPS△AOB=2.
过点P作PM⊥y轴于点M,
∴S△BOP OB PM=2,即4PM=2,
∴PM=1,即点P的横坐标为1,
当x=1时,y1+4;
∴点P的坐标为(1,).
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,则∠BAC=45°,如图,过点B作BD⊥AB交直线AC于点D,过点D作DE⊥y轴于点E,
∴∠BED=∠AOB=90°,
∴∠ABO+∠OBD=∠BDE+∠OBE=90°,
∴∠ABO=∠BDE,
∵∠BAC=45°,
∴∠BDA=45°,
∴BD=AB,
∴△BDE≌△ABO(AAS),
∴BE=OA=3,DE=OB=4,
∴OE=OB﹣BE=1,
∴D(﹣4,1),
设直线AC的解析式为:y=mx+n,
∴,解得,
∴直线AC的表达式为:yx.
8.【解答】解:(1)在中,
当x=0时,y=4,
当y=0时,得:,
解得:x=8,
∴A(8,0)、B(0,4),
∴OA=8,OB=4,
联立与,
解得:,
∴点C(2,3),
由题意得:点D(3,﹣3);
(2)作点D关于y轴的对称点D′,则D′(﹣3,﹣3),
连接CD′交y轴于点P′,
连接P′D,此时CP′+PD最小,
设直线CD′的解析式为y=kx+b,把点C(2,3),D′(﹣3,﹣3)代入得:
,
解得:,
∴直线CD′的解析式为,
当x=0时,,
∴点,
即当CP+PD最小时,点P的坐标为;
(3)设点Q(x,0),
∵D(3,﹣3),O(0,0),
∴OD2=(3﹣0)2+(﹣3﹣0)2=18,
OQ2=(x﹣0)2+(0﹣0)2=x2,
DQ2=(x﹣3)2+(0+3)2=(x﹣3)2+9,
当△OQD为等腰三角形时,分三种情况讨论:
当OD=OQ时,由18=x2得:,
∴或,
当OD=DQ时,由18=(x﹣3)2+9得:
x=6或x=0(与O重合,舍去),
∴Q(6,0),
当OQ=DQ时,由x2=(x﹣3)2+9得:x=3,
∴Q(3,0),
综上,△OQD为等腰三角形时,点Q坐标为,或,或Q(3,0)或Q(6,0).
9.【解答】解:(1)①由A(8,0),B(0,6),
设直线AB解析式为y=kx+b,
把A与B坐标代入得,
解得,
则直线AB解析式为yx+6;
②∵QA=QO,OA=8,
∴xQ=4,
∵点P关于y轴的对称点为Q,
∴xP=﹣4,
代入直线AP解析式得(﹣4)+6=9,
则P坐标得P(﹣4,9);
(2)①若∠QAC=90°,如图1所示,
∴xQ=8,
∴a=xP=﹣8,
∴AC=AQ=16,即P(﹣8,16),
∴直线AP解析式为y=﹣x+8,
∴a=﹣8,b=8;
②若∠AQC=90°,如图2所示,
则AC=8﹣a=4CO=﹣4a,
∴a,
∴xP,yP=yq,即P(,),
∴直线AP解析式为yx+4,
∴a,b=4,
③P、Q重合于(0,8)时,△QCA也是等腰直角三角形,此时a=0,b=8,舍去,
综上所示,a=﹣8,b=8或a,b=4.
10.【解答】解:(1)设直线AB的解析式为:y=kx+b,
∵点A的坐标是(0,4),点B的坐标是(8,0),且A、B两点都在直线AB上,
∴,
解得,
∴对角线AB所在直线的函数关系式为:y;
(2)∵点A的坐标是(0,4),点B的坐标是(8,0),
∴OA=4,OB=8,
∵MN是AB的垂直平分线,
∴MA=MB,
在Rt△AOM中,由勾股定理得:
∴42+(8﹣AM)2=AM2,
∴AM=5;
(3)长方形AOBC的面积为:4×8=32,设点P的纵坐标为y,
当点P在第二象限时,
由S△BMP﹣S△AMB=S△PAM=S矩形AOBC,
∴32,
解得:y,
当y时,,
解得:x,
当点P在第四象限时,
同理可知:S△BMP+S△AMB=S△PAM=S矩形AOBC,
,
解得:y,
当y时,,
解得:x,
∴点P的坐标为:()或().
11.【解答】解:(1)将 (﹣3,0),(1,8)代入y=kx+b得:,
解得:;
即k=2,b=6;
(2)∵k=2,b=6,
∴y=2x+6,
令x=0,则y=6,
∴B(0,6),
∴OB=6,
∵A(﹣3,0),
∴OA=3,
∵△COD≌△AOB,
∴OD=OB=6,
∴D(6,0),
∴AD=OA+OD=3+6=9,
∴t=9,
∴t=9s时△COD≌△AOB,
此时D的坐标为(6,0);
(3)当D在x轴上运动时△COD是直角三角形,
∵C(3,0),
∴OC=3,
当0≤t<3时,OA=3,AD=t,
∴OD=3﹣t,
∴SDO×OC(3﹣t)×3t;
当t≥3时,OA=3,AD=t,
∴OD=t﹣3
∴SDO×OC(t﹣3)×3t;
即S.
12.【解答】解:(1)把点A(0,5),B(4,1)代入y=kx+b得,,
解得,
∴直线AB的函数表达式为y=﹣x+5;
(2)在y=﹣x+5中,令y=0,则x=5,
∴C(5,0),
∴不等式kx+b>0的解集为x<5;
(3)解得,
∴D(2,3),
设P(m,﹣m+5),
∵直线y=2x﹣1与y轴交于点E,
∴E(0,﹣1),
∴OE=1,
∵S△AED=2S△AEP,
∴AE xD=2AE xP,
∴6×2=26 |m|,
∴m=±1,
∴P(1,4)或(﹣1,6).
13.【解答】解:(1)设直线AB的解析式是y=kx+b,
根据题意得:,
解得:,
则直线的解析式是:y=﹣x+6;
(2)在y=﹣x+6中,令x=0,解得:y=6,
S△OAC6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m,
则直线的解析式是:yx,
∵当△OMC的面积是△OAC的面积的时,
∴当M的横坐标是4=1,
在yx中,当x=1时,y,则M的坐标是(1,);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,)或M2(1,5).
当M的横坐标是:﹣1,
在y=﹣x+6中,当x=﹣1时,y=7,则M的坐标是(﹣1,7);
综上所述:M的坐标是:M1(1,)或M2(1,5)或M3(﹣1,7).
14.【解答】解:(1)如图1所示,过点C作CE⊥x轴于点E,
∵将线段AB绕点A顺时针旋转90°得到线段AC,
∴AB=AC,∠BAC=90°,
又∵∠BOA=∠AEC=90°,
∴∠OAB=90°﹣∠CAE=∠ACE,
∴△OAB≌△ECA(AAS),
∴OA=CE,OB=AE,
∵点A和点B坐标分别为(1,0)和(0,3),
∴OE=OA+AE=1+3=4,
∴C(4,1),
设直线BD的解析式为y=kx+b,
∴,
解得:,
∴直线BD的解析式为;
(2)如图2,过点P作PQ⊥x轴于Q,
设点P的坐标为,
当y=0时,,
∴x=6,
∴D(6,0),AD=6﹣1=5,
∵S△ABP=S△BAD﹣S△PAD,
∴,
,
解得:m=2,
∴P(2,2);
(3)当直线y=﹣x+m经过点C(4,1)时,1=﹣4+m,
解得:m=5,
当直线y=﹣x+m经过点A(1,0)时,0=﹣1+m,
解得:m=1
观察图形可得:直线y=﹣x+m与△ABC有公共点,则1≤m≤5.
15.【解答】解:(1)∵直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),
∴5=1+b,
∴b=4,
∴直线l2:y=﹣x+4,
∵直线l2:y=﹣x+4经过点C(2,m),
∴m=﹣2+4=2,
∴C(2,2),
把C(2,2)代入y=kx+1,得到k.
∴k,b=4,m=2;
(2)对于直线l1:yx+1,令y=0,得到x=﹣2,
∴D(﹣2,0),
∴OD=2,
对于直线l2:y=﹣x+4,令y=0,得到x=4,
∴A(4,0),
∴OA=4,AD=6,
∵C(2,2),
∴S△ADC6×2=6;
(3)作点C关于x轴的对称点C′,连接BC′交x轴于E,连接EC,则△BCE的周长最小.
∵B(﹣1,5),C(2,2)关于x轴的对称点是(2,﹣2),
则设经过(2,﹣2)和B(﹣1,5)的函数解析式是y=mx+n,
则,
解得:,
则直线的解析式是yx.
令y=0,则x0,解得:x.
则E的坐标是(,0).
∴存在一点E,使△BCE的周长最短,E(,0).
16.【解答】解:(1)对于,当x=0时,y=﹣4,当y=0时,x=3,
∴点A的坐标为(3,0),点B的坐标为(0,﹣4);
故答案为(3,0);(0,﹣4);
(2)在x轴上存在点P,使得2∠BPO+∠OBA=90°,
∵点A的坐标为(3,0),点B的坐标为(0,﹣4),
∴OA=3,OB=4,
在Rt△OAB中,∠OAB+∠OBA=90°,
由勾股定理得:AB5,
∵2∠BPO+∠OBA=90°,
∴∠OAB=2∠BPO,
∴有以下两种情况:
①当点P在点A的右侧时,如图1所示:
∵∠OAB是△BAP的一个外角,
∴∠OAB=∠BPO+∠ABP,
∴2∠BPO=∠BPO+∠ABP,
∴∠BPO=∠ABP,
∴AP=AB=5,
∴OP=OA+AP=3﹣5=8,
∴点P的坐标为(8,0);
②当点P在点A的左侧时,作点A关于y轴的对称点E,连接BE,如图2所示:
∵OE=OA=3,BE=AB=5,∠OEB=∠OAB=2∠BPO,
∵∠OEB是△BPE的一个外角,
∴∠OEB=∠BPO+∠EBP=2∠BPO,
∴∠BPO=∠EBP,
∴PE=BE=5,
∴OP=OE+PE=3+5=8,
∴点P的坐标为(﹣8,0),
综上所述:点P的坐标为(8,0)或(﹣8,0);
(3)对于,当x=0时,y=2,当y=0时,x=﹣12,
∴点C的坐标为(﹣12,0),点D的坐标为(0,5),
∴OC=12,OD=5,
当△CDQ为等腰直角三角形时,有以下6中情况:
①当以点D为直角顶点,CD为腰,点Q在CD的上方时,过点Q作QF⊥y轴于点F,如图3所示:
∴∠COQ=90°,CD=DQ,∠COD=∠DFQ=90°,
∴∠CDO+∠QDF=90°,∠OCD+∠CDO=90°,
∴∠OCD=∠QDF,
在△OCD和△QDF中,
,
∴△OCD≌△QDF(AAS),
∴OD=QF=5,OC=DF=12,
∴OF=OD+DF=5+12=17,
∴点Q的坐标为(﹣5,17);
②当以点D为直角顶点,CD为腰,点Q在CD的下方时,过点Q作QFH⊥y轴于点H,如图4所示:
同理可证明:△OCD≌△HDQ(AAS),
∴OD=HQ=5,OC=DH=12,
∴OH=DH﹣OD=12﹣5=7,
∴点Q的坐标为(5,﹣7);
③当以点C为直角顶点,CD为腰,点Q在CD的上方时,过点Q作QG⊥x轴于点G,如图5所示:
同理可证明:△OCD≌△GQC(AAS),
∴OC=QG=12,OD=CG=5,
∴OD=OC+CG=12+5=17,
∴点Q的坐标为(﹣17,12);
④当以点C为直角顶点,CD为腰,点Q在CD的下方时,过点Q作QK⊥x轴于点K,如图6所示:
同理可证明:△OCD≌△KQC(AAS),
∴OD=CK=5,OC=KQ=12,
∴OK=OC﹣CK=12﹣5=7,
∴点Q的坐标为(﹣7,﹣12);
⑤当以CD为斜边,∠CQD=90°,且点Q在CD的上方时,过点Q作QT⊥x轴于点T,QR⊥y轴于点R,如图7所示:
∴∠QTO=∠QRO=∠TOR=90°,
∴四边形QTOR是矩形,
同理可证明:△QCT≌△QDR(AAS),
∴设CT=DR=a,QT=QR,
∴矩形QTOR是正方形,
∴OT=OR=a,
∵OT=OC﹣CT=12﹣a,OR=OD+DR=5+a,
∴12﹣a=5+a,
解得:a=3.5,
∴OT=12﹣a=8.5,
∴点Q的坐标为(﹣8.5,8.5);
⑥当以CD为斜边,∠CQD=90°,且点Q在CD的下方时,过点Q作OM⊥x轴于点M,QN⊥y轴于点N,如图8所示:
∴四边形QMON为矩形,
同理可证明:△QCM≌△QDN(AAS),
∴设QM=QN=a,CM=DN,
∴矩形QMON是正方形,
∴OM=ON=a,
∵CM=OC﹣OM=12﹣a,DN=OD+ON=5+a,
∴12﹣a=5+a,
解得:a=3.5,
∴QM=QN=3.5,
∴点Q的坐标为(﹣3.5,﹣3.5),
综上所述:所有满足条件的点Q的坐标为(﹣5,17)或(5,﹣7)或(﹣17,12)或(﹣7,﹣12)或(﹣8.5,8.5)或(﹣3.5,﹣3.5).
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练一次函数与几何相关综合问题
1.如图,直线l1:y=﹣2x+4与x轴交于点B,OB=OC,直线l2:y=kx+b经过点C,且与l1交于点A(1,2).
(1)求直线l2的解析式;
(2)记直线l2与y轴的交点为D,记直线l1与y轴的交点为E,求△ADE的面积;
(3)根据图象,直接写出0≤﹣2x+4<kx+b的解集.
2.如图1,在平面直角坐标系中,直线AB与x轴交于点A(m,0),与y轴交于点B(0,n),且m,n满足:(m+n)2+|n﹣6|=0.
(1)求△AOB的面积;
(2)C为OA延长线上一动点,以BC为直角边作等腰直角△BCE,连接EA,求直线EA与y轴交点F的坐标;
(3)在(2)的条件下,当AC=4时,在坐标平面内是否存在一点P,使以B,E,F,P为顶点的四边形是平行四边形,如果存在,直接写出点P的坐标,若不存在,说明理由.
3.如图,点A、B分别在x轴和y轴的正半轴上,以线段AB为边在第一象限作等边△ABC,S△ABC,且CA∥y轴,点C在反比例函数y(k≠0,x>0)的图象上.
(1)求该反比例函数的解析式;
(2)若点N是反比例函数图象上一点,当四边形ABCN是菱形时,求出点N坐标.
4.如图,反比例函数y(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a)、B两点,点C在第四象限,BC∥x轴.
(1)求k的值;
(2)以AB、BC为边作菱形ABCD,求D点坐标.
5.如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(6,8),一次函数的图象与边OC、AB分别交于点D、E,点M是线段DE上的一个动点.
(1)求E点的坐标;
(2)连接OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点M的坐标.
6.如图,在平面直角坐标系中,直线l1:y=kx+8分别交x轴,y轴于点A,B,点A(8,0).直线l2:经过线段AB的中点Q,分别交x轴,y轴于点C,D.
(1)请直接写出k的值;
(2)请求出直线l2的解析式;
(3)点P(t,0)为x轴上一动点,过点P作PE∥y轴交l1,l2于点E,F;
①当EF=2EP时,求t的值.
②连接BC,当∠OBC=∠ABF时,求t的值.
7.如图,在平面直角坐标系xOy中,直线y=kx+4与x轴、y轴分别交于A、B两点,4OA=3OB.
(1)求k的值;
(2)点P在线段AB上,连接OP.若S△AOB=3S△BOP,求点P的坐标;
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,求直线AC的表达式.
8.如图1,一次函数的图象与x轴、y轴分别交于点A、点B,与正比例函数的图象交于点C,将点C向右平移1个单位,再向下平移6个单位得到点D.
(1)求OA、OB的长度和点D的坐标;
(2)如图2,点P是y轴上一动点,当CP+PD最小时,求点P的坐标;
(3)若点Q是x轴上一动点,当△OQD为等腰三角形时,求出点Q的坐标.
9.如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(8,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
(1)当b=6时,
①求直线AB的解析式;②若QO=QA,求P点的坐标.
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
10.如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点A的坐标是(0,4),点B的坐标是(8,0).
(1)求对角线AB所在直线的函数关系式;
(2)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;
(3)在(2)的条件下,若点P是直线AB上的一个动点,当△PAM的面积与长方形AOBC的面积相等时,求点P的坐标.
11.如图,已知直线l:y=kx+b与x轴交于A(﹣3,0)、与y轴交于B点,且经过(1,8),在y轴上有一点C(0,3),动点D从点A以每秒1个单位的速度沿x轴向右移动,设动点D的移动时间为t秒.
(1)求k、b的值;
(2)当t为何值时△COD≌△AOB,并求此时点D的坐标;
(3)求△COD的面积S与动点D的移动时间t之间的函数关系式.
12.如图,已知直线y=kx+b经过点A(0,5),B(4,1),并与x轴交于点C,与直线y=2x﹣1相交于点D.
(1)求直线AB的函数表达式;
(2)求不等式kx+b>0的解集;
(3)直线y=2x﹣1与y轴交于点E,在直线AB上是否存在点P,使得S△AED=2S△AEP,若存在,直接写出点P的坐标,若不存在,说明理由.
13.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的?若存在求出此时点M的坐标;若不存在,说明理由.
14.如图1,已知点A和点B坐标分别为(1,0)和(0,3),将线段AB绕点A顺时针旋转90°得到线段AC,连接BC交x轴于点D.
(1)求直线BD的函数关系式;
(2)如图2,若点P为线段BD上一点,且△ABP的面积为,求点P的坐标;
(3)若直线y=﹣x+m与△ABC有公共点,直接写出m的取值范围.
15.如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)求△ADC的面积;
(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.
16.在平面直角坐标系中,一次函数的图象l1与x轴、y轴分别交于点A、B,一次函数的图象l2与x轴、y轴分别交于点C、D.
(1)填空:点A的坐标为 (3,0) ,点B的坐标为 (0,﹣4) ;
(2)在x轴上是否存在点P,使得2∠BPO+∠OBA=90°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)点Q为平面内一点,且△CDQ为等腰直角三角形,请直接写出所有满足条件的点Q的坐标.
参考答案
1.【解答】解:(1)∵l1的直线解析式为y=﹣2x+4,
当y=0时,x=2,
∴B(2,0),
∵OB=OC,
∴C(﹣2,0),
∵l2:y=kx+b经过点C和点A,
,
解得,
∴l2的直线解析式为;
(2)在直线l1的解析式y=﹣2x+4中,
当x=0时,y=4,
∴E(0,4),
在直线l2的解析式中,当x=0时,,
∴,
∴,
∴;
(3)由函数图象可知,0≤﹣2x+4<kx+b的解集为1<x≤2.
2.【解答】解:(1)∵(m+n)2+|n﹣6|=0,
∴n﹣6=0且m+n=0,
解得:,
即点A、B的坐标分别为(﹣6,0)、(0,6),则OA=OB=6,
∴S△AOBOA×OB6×6=18;
(2)如图所示,过点E作EG⊥x轴于G.
∵△ECB为等腰直角三角形,
∴CE=CB,∠ECB=90°,
∴∠ECG+∠OCB=180°﹣90°=90°,
∵EG⊥GC,
∴Rt△EGC中,∠GEC+∠ECG=180°﹣∠EGC=180°﹣90°=90°,
∴∠GEC=∠OCB,
在△ECG和△CBO中:
,
∴△ECG≌△CBO(AAS),
∴CG=BO=6,EG=OC,
设AC=a,
∴OC=OA+AC=6+a=EG,
∴OG=OC+CG=6+a+6=12+a,
∴E点的坐标为(﹣12﹣a,6+a),
∵A(﹣6,0),
由点A、E的坐标得,EA的解析式为y=﹣x﹣6,
∴当x=0时,y=﹣6,
∴EA与y轴的交点坐标为(0,﹣6),
即点F(0,﹣6);
(3)存在,点P的坐标为 (16,﹣10),(﹣16,22),(﹣16,﹣2).
∵AD=a=4,E(﹣12﹣a,6+a),
∴E(﹣16,10),
又∵以B、E、F、P为顶点的四边形是平行四边形,且F(0,﹣6),B(0,6),
设P(a,b),
当BF为对角线时,得:
,
解得:,
∴P(16,﹣10);
当BE为对角线时,得:
,
解得:,
∴P(﹣16,22),
当EF为对角线时,得:
,
解得:,
∴P(﹣16,﹣2)综上所述,点P的坐标为 (16,﹣10),(﹣16,22),(﹣16,﹣2).
3.【解答】解:(1)根据题意,设C点的坐标为(a,b),
∴b,
∴ab=k,即得AC OA=k,
又∵CA∥y轴,
∴S△ABCAC OA,
∴k,
即k=2,
∴反比例函数的解析式为y;
(2)如图,根据菱形的性质可知,AC⊥BN,且AC与BN互相平分,
设菱形对角线的交点为P,设C点坐标为(a,b),
∵△ABC是等边三角形,四边形ABCN是菱形,
∴P(a,b),N(2a,b),
即BP=OA=a,AP=CPb,
∵∠BAC=60°,
∴BP=AP×tan60°,
即ab,
由(1)知ab=2,C点在第一象限,
∴a,b=2,
∴N(2,1).
4.【解答】解:(1)∵点A(1,a)在直线y=2x上,
∴a=2×1=2,
即点A的坐标为(1,2),
∵点A(1,2)是反比例函数y(k≠0)的图象与正比例函数y=2x图象的交点,
∴k=1×2=2,
即k的值是2;
(2)由题意得:2x,
解得:x=1或﹣1,
经检验x=1或﹣1是原方程的解,
∴B(﹣1,﹣2),
∵点A(1,2),
∴AB2,
∵菱形ABCD是以AB、BC为边,且BC∥x轴,
∴AD=AB=2,
∴D(1+2,2).
5.【解答】解:(1)一次函数中,
令x=0,得y=6,
∴D的坐标是(0,6),OD=6,
∵OD=BE,
∴BE=6,
∴E的坐标是(6,2);
(2)S四边形OAED(OD+AE) OA(6+2)×6=24,
∵三角形ODM的面积与四边形OAEM的面积之比为1:3,
∴S△ODM=6.
设M的横坐标是a,则6a=6,
解得:a=2,
把x=a=2代入得:
,
∴M的坐标;
故点M的坐标为;
(3)当四边形OMDN是菱形时,如图(1),
此时,M的纵坐标是3,把y=3代入中,
解得:,
∴M的坐标是;
当四边形OMND是菱形时,如图(2),
∵OM=OD=6,则设M的横坐标是m,则纵坐标是,
∴,
解得:或0(舍去),
∴M的坐标是,
综上,点M的坐标为或.
6.【解答】解:(1)∵A(8,0)过直线l1:y=kx+8,
∴0=k×8+8,
解得:k=﹣1,
∴k=﹣1;
(2)∵l1:y=﹣x+8分别交x轴,y轴于点A,B,
∴B(0,8),
∵AB的中点Q,A(8,0),
∴Q()即Q(4,4),
∵l2:yx+b过Q点,
∴44+b,
解得:b=2,
∴l2:yx+2;
(3)∵P(t,0)为x轴上一动点,过点P作PE∥y轴交l1:y=﹣x+8,l2:yx+2于点E,F;
∴E(t,﹣t+8),F(t,t+2),
t=20,或t;
②∵P(t,0)为x轴上一动点,过点P作PE∥y轴交l1:y=﹣x+8,l2:yx+2于点E,F;
∴E(t,﹣t+8),F(t,t+2),
∵A(8,0),B(0,8),
∴OA=OB=8,
∵∠AOB=90°,
∴∠ABO=45°,ABAO=8,
∵l2:yx+2交x轴于C点,
∴C(﹣4,0),
∵B(0,8),
∴OB=2CO,
当∠OBC=∠ABF时,分两种情况:
F在l1上方时,如图:
过A作AM⊥AB交AF延长线于M点,
∴∠BAM=90°,
∴∠MAN=45°,
作MN⊥x轴于N点,则△AMN是等要直角三角形,
∴AN=MN,
∴∠BAM=∠AOB=90°,∠OBC=∠ABF,
∴△BOC∽△BAM,
∴,即,
解得:AM=4,
∴AN=MN=4,
∴AN=OA+AN=8+4=12,
∴N(12,0),M(12,4),
由B(0,8),
设直线BM:y=nx+8,
∴4=12n+8,
解得:n,
∴BM:yx+8,
∵BM:yx+8过点F(t,t+2),
∴t+2t+8,
解得:t=7.2;
F在l1下方时,如图,
若BF交x轴于N点,过N点作NM⊥AB于M点,
同理:∴△BOC∽△BAM,△AMN是等腰直角三角形,
∴,ANAMNM,
∵BM=AB﹣AM=AB﹣MN=8MN,
∴,
解得:MN,
∴AN,
∴ON=AO﹣AN=8,
∴N(,0),
由B(0,8),
设直线BN:y=nx+8,
∴0n+8,
解得:n=﹣3,
∴BN:y=﹣3x+8,
∵BN:y=﹣3x+8过点F(t,t+2),
∴t+2=﹣3t+8,
解得:t,
综上所述:∠OBC=∠ABF时,t=7.2或.
7.【解答】解:(1)直线y=kx+4中,令x=0,则y=4,
∴B(0,4),
∴OB=4,
∵4OA=3OB,
∴OA=3,
由图可知点A在x轴的正半轴,
∴A(3,0),
∴3k+4=0,
∴k.
(2)由(1)知OA=3,OB=4,yx+4,
∴S△AOB OA OB3×4=6,
∵S△AOB=3S△BOP,
∴S△BOPS△AOB=2.
过点P作PM⊥y轴于点M,
∴S△BOP OB PM=2,即4PM=2,
∴PM=1,即点P的横坐标为1,
当x=1时,y1+4;
∴点P的坐标为(1,).
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,则∠BAC=45°,如图,过点B作BD⊥AB交直线AC于点D,过点D作DE⊥y轴于点E,
∴∠BED=∠AOB=90°,
∴∠ABO+∠OBD=∠BDE+∠OBE=90°,
∴∠ABO=∠BDE,
∵∠BAC=45°,
∴∠BDA=45°,
∴BD=AB,
∴△BDE≌△ABO(AAS),
∴BE=OA=3,DE=OB=4,
∴OE=OB﹣BE=1,
∴D(﹣4,1),
设直线AC的解析式为:y=mx+n,
∴,解得,
∴直线AC的表达式为:yx.
8.【解答】解:(1)在中,
当x=0时,y=4,
当y=0时,得:,
解得:x=8,
∴A(8,0)、B(0,4),
∴OA=8,OB=4,
联立与,
解得:,
∴点C(2,3),
由题意得:点D(3,﹣3);
(2)作点D关于y轴的对称点D′,则D′(﹣3,﹣3),
连接CD′交y轴于点P′,
连接P′D,此时CP′+PD最小,
设直线CD′的解析式为y=kx+b,把点C(2,3),D′(﹣3,﹣3)代入得:
,
解得:,
∴直线CD′的解析式为,
当x=0时,,
∴点,
即当CP+PD最小时,点P的坐标为;
(3)设点Q(x,0),
∵D(3,﹣3),O(0,0),
∴OD2=(3﹣0)2+(﹣3﹣0)2=18,
OQ2=(x﹣0)2+(0﹣0)2=x2,
DQ2=(x﹣3)2+(0+3)2=(x﹣3)2+9,
当△OQD为等腰三角形时,分三种情况讨论:
当OD=OQ时,由18=x2得:,
∴或,
当OD=DQ时,由18=(x﹣3)2+9得:
x=6或x=0(与O重合,舍去),
∴Q(6,0),
当OQ=DQ时,由x2=(x﹣3)2+9得:x=3,
∴Q(3,0),
综上,△OQD为等腰三角形时,点Q坐标为,或,或Q(3,0)或Q(6,0).
9.【解答】解:(1)①由A(8,0),B(0,6),
设直线AB解析式为y=kx+b,
把A与B坐标代入得,
解得,
则直线AB解析式为yx+6;
②∵QA=QO,OA=8,
∴xQ=4,
∵点P关于y轴的对称点为Q,
∴xP=﹣4,
代入直线AP解析式得(﹣4)+6=9,
则P坐标得P(﹣4,9);
(2)①若∠QAC=90°,如图1所示,
∴xQ=8,
∴a=xP=﹣8,
∴AC=AQ=16,即P(﹣8,16),
∴直线AP解析式为y=﹣x+8,
∴a=﹣8,b=8;
②若∠AQC=90°,如图2所示,
则AC=8﹣a=4CO=﹣4a,
∴a,
∴xP,yP=yq,即P(,),
∴直线AP解析式为yx+4,
∴a,b=4,
③P、Q重合于(0,8)时,△QCA也是等腰直角三角形,此时a=0,b=8,舍去,
综上所示,a=﹣8,b=8或a,b=4.
10.【解答】解:(1)设直线AB的解析式为:y=kx+b,
∵点A的坐标是(0,4),点B的坐标是(8,0),且A、B两点都在直线AB上,
∴,
解得,
∴对角线AB所在直线的函数关系式为:y;
(2)∵点A的坐标是(0,4),点B的坐标是(8,0),
∴OA=4,OB=8,
∵MN是AB的垂直平分线,
∴MA=MB,
在Rt△AOM中,由勾股定理得:
∴42+(8﹣AM)2=AM2,
∴AM=5;
(3)长方形AOBC的面积为:4×8=32,设点P的纵坐标为y,
当点P在第二象限时,
由S△BMP﹣S△AMB=S△PAM=S矩形AOBC,
∴32,
解得:y,
当y时,,
解得:x,
当点P在第四象限时,
同理可知:S△BMP+S△AMB=S△PAM=S矩形AOBC,
,
解得:y,
当y时,,
解得:x,
∴点P的坐标为:()或().
11.【解答】解:(1)将 (﹣3,0),(1,8)代入y=kx+b得:,
解得:;
即k=2,b=6;
(2)∵k=2,b=6,
∴y=2x+6,
令x=0,则y=6,
∴B(0,6),
∴OB=6,
∵A(﹣3,0),
∴OA=3,
∵△COD≌△AOB,
∴OD=OB=6,
∴D(6,0),
∴AD=OA+OD=3+6=9,
∴t=9,
∴t=9s时△COD≌△AOB,
此时D的坐标为(6,0);
(3)当D在x轴上运动时△COD是直角三角形,
∵C(3,0),
∴OC=3,
当0≤t<3时,OA=3,AD=t,
∴OD=3﹣t,
∴SDO×OC(3﹣t)×3t;
当t≥3时,OA=3,AD=t,
∴OD=t﹣3
∴SDO×OC(t﹣3)×3t;
即S.
12.【解答】解:(1)把点A(0,5),B(4,1)代入y=kx+b得,,
解得,
∴直线AB的函数表达式为y=﹣x+5;
(2)在y=﹣x+5中,令y=0,则x=5,
∴C(5,0),
∴不等式kx+b>0的解集为x<5;
(3)解得,
∴D(2,3),
设P(m,﹣m+5),
∵直线y=2x﹣1与y轴交于点E,
∴E(0,﹣1),
∴OE=1,
∵S△AED=2S△AEP,
∴AE xD=2AE xP,
∴6×2=26 |m|,
∴m=±1,
∴P(1,4)或(﹣1,6).
13.【解答】解:(1)设直线AB的解析式是y=kx+b,
根据题意得:,
解得:,
则直线的解析式是:y=﹣x+6;
(2)在y=﹣x+6中,令x=0,解得:y=6,
S△OAC6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m,
则直线的解析式是:yx,
∵当△OMC的面积是△OAC的面积的时,
∴当M的横坐标是4=1,
在yx中,当x=1时,y,则M的坐标是(1,);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,)或M2(1,5).
当M的横坐标是:﹣1,
在y=﹣x+6中,当x=﹣1时,y=7,则M的坐标是(﹣1,7);
综上所述:M的坐标是:M1(1,)或M2(1,5)或M3(﹣1,7).
14.【解答】解:(1)如图1所示,过点C作CE⊥x轴于点E,
∵将线段AB绕点A顺时针旋转90°得到线段AC,
∴AB=AC,∠BAC=90°,
又∵∠BOA=∠AEC=90°,
∴∠OAB=90°﹣∠CAE=∠ACE,
∴△OAB≌△ECA(AAS),
∴OA=CE,OB=AE,
∵点A和点B坐标分别为(1,0)和(0,3),
∴OE=OA+AE=1+3=4,
∴C(4,1),
设直线BD的解析式为y=kx+b,
∴,
解得:,
∴直线BD的解析式为;
(2)如图2,过点P作PQ⊥x轴于Q,
设点P的坐标为,
当y=0时,,
∴x=6,
∴D(6,0),AD=6﹣1=5,
∵S△ABP=S△BAD﹣S△PAD,
∴,
,
解得:m=2,
∴P(2,2);
(3)当直线y=﹣x+m经过点C(4,1)时,1=﹣4+m,
解得:m=5,
当直线y=﹣x+m经过点A(1,0)时,0=﹣1+m,
解得:m=1
观察图形可得:直线y=﹣x+m与△ABC有公共点,则1≤m≤5.
15.【解答】解:(1)∵直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),
∴5=1+b,
∴b=4,
∴直线l2:y=﹣x+4,
∵直线l2:y=﹣x+4经过点C(2,m),
∴m=﹣2+4=2,
∴C(2,2),
把C(2,2)代入y=kx+1,得到k.
∴k,b=4,m=2;
(2)对于直线l1:yx+1,令y=0,得到x=﹣2,
∴D(﹣2,0),
∴OD=2,
对于直线l2:y=﹣x+4,令y=0,得到x=4,
∴A(4,0),
∴OA=4,AD=6,
∵C(2,2),
∴S△ADC6×2=6;
(3)作点C关于x轴的对称点C′,连接BC′交x轴于E,连接EC,则△BCE的周长最小.
∵B(﹣1,5),C(2,2)关于x轴的对称点是(2,﹣2),
则设经过(2,﹣2)和B(﹣1,5)的函数解析式是y=mx+n,
则,
解得:,
则直线的解析式是yx.
令y=0,则x0,解得:x.
则E的坐标是(,0).
∴存在一点E,使△BCE的周长最短,E(,0).
16.【解答】解:(1)对于,当x=0时,y=﹣4,当y=0时,x=3,
∴点A的坐标为(3,0),点B的坐标为(0,﹣4);
故答案为(3,0);(0,﹣4);
(2)在x轴上存在点P,使得2∠BPO+∠OBA=90°,
∵点A的坐标为(3,0),点B的坐标为(0,﹣4),
∴OA=3,OB=4,
在Rt△OAB中,∠OAB+∠OBA=90°,
由勾股定理得:AB5,
∵2∠BPO+∠OBA=90°,
∴∠OAB=2∠BPO,
∴有以下两种情况:
①当点P在点A的右侧时,如图1所示:
∵∠OAB是△BAP的一个外角,
∴∠OAB=∠BPO+∠ABP,
∴2∠BPO=∠BPO+∠ABP,
∴∠BPO=∠ABP,
∴AP=AB=5,
∴OP=OA+AP=3﹣5=8,
∴点P的坐标为(8,0);
②当点P在点A的左侧时,作点A关于y轴的对称点E,连接BE,如图2所示:
∵OE=OA=3,BE=AB=5,∠OEB=∠OAB=2∠BPO,
∵∠OEB是△BPE的一个外角,
∴∠OEB=∠BPO+∠EBP=2∠BPO,
∴∠BPO=∠EBP,
∴PE=BE=5,
∴OP=OE+PE=3+5=8,
∴点P的坐标为(﹣8,0),
综上所述:点P的坐标为(8,0)或(﹣8,0);
(3)对于,当x=0时,y=2,当y=0时,x=﹣12,
∴点C的坐标为(﹣12,0),点D的坐标为(0,5),
∴OC=12,OD=5,
当△CDQ为等腰直角三角形时,有以下6中情况:
①当以点D为直角顶点,CD为腰,点Q在CD的上方时,过点Q作QF⊥y轴于点F,如图3所示:
∴∠COQ=90°,CD=DQ,∠COD=∠DFQ=90°,
∴∠CDO+∠QDF=90°,∠OCD+∠CDO=90°,
∴∠OCD=∠QDF,
在△OCD和△QDF中,
,
∴△OCD≌△QDF(AAS),
∴OD=QF=5,OC=DF=12,
∴OF=OD+DF=5+12=17,
∴点Q的坐标为(﹣5,17);
②当以点D为直角顶点,CD为腰,点Q在CD的下方时,过点Q作QFH⊥y轴于点H,如图4所示:
同理可证明:△OCD≌△HDQ(AAS),
∴OD=HQ=5,OC=DH=12,
∴OH=DH﹣OD=12﹣5=7,
∴点Q的坐标为(5,﹣7);
③当以点C为直角顶点,CD为腰,点Q在CD的上方时,过点Q作QG⊥x轴于点G,如图5所示:
同理可证明:△OCD≌△GQC(AAS),
∴OC=QG=12,OD=CG=5,
∴OD=OC+CG=12+5=17,
∴点Q的坐标为(﹣17,12);
④当以点C为直角顶点,CD为腰,点Q在CD的下方时,过点Q作QK⊥x轴于点K,如图6所示:
同理可证明:△OCD≌△KQC(AAS),
∴OD=CK=5,OC=KQ=12,
∴OK=OC﹣CK=12﹣5=7,
∴点Q的坐标为(﹣7,﹣12);
⑤当以CD为斜边,∠CQD=90°,且点Q在CD的上方时,过点Q作QT⊥x轴于点T,QR⊥y轴于点R,如图7所示:
∴∠QTO=∠QRO=∠TOR=90°,
∴四边形QTOR是矩形,
同理可证明:△QCT≌△QDR(AAS),
∴设CT=DR=a,QT=QR,
∴矩形QTOR是正方形,
∴OT=OR=a,
∵OT=OC﹣CT=12﹣a,OR=OD+DR=5+a,
∴12﹣a=5+a,
解得:a=3.5,
∴OT=12﹣a=8.5,
∴点Q的坐标为(﹣8.5,8.5);
⑥当以CD为斜边,∠CQD=90°,且点Q在CD的下方时,过点Q作OM⊥x轴于点M,QN⊥y轴于点N,如图8所示:
∴四边形QMON为矩形,
同理可证明:△QCM≌△QDN(AAS),
∴设QM=QN=a,CM=DN,
∴矩形QMON是正方形,
∴OM=ON=a,
∵CM=OC﹣OM=12﹣a,DN=OD+ON=5+a,
∴12﹣a=5+a,
解得:a=3.5,
∴QM=QN=3.5,
∴点Q的坐标为(﹣3.5,﹣3.5),
综上所述:所有满足条件的点Q的坐标为(﹣5,17)或(5,﹣7)或(﹣17,12)或(﹣7,﹣12)或(﹣8.5,8.5)或(﹣3.5,﹣3.5).
21世纪教育网(www.21cnjy.com)
同课章节目录
