2025年九年级中考数学三轮冲刺训练一次函数中角度相关问题训练(含答案)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练一次函数中角度相关问题训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练一次函数中角度相关问题训练
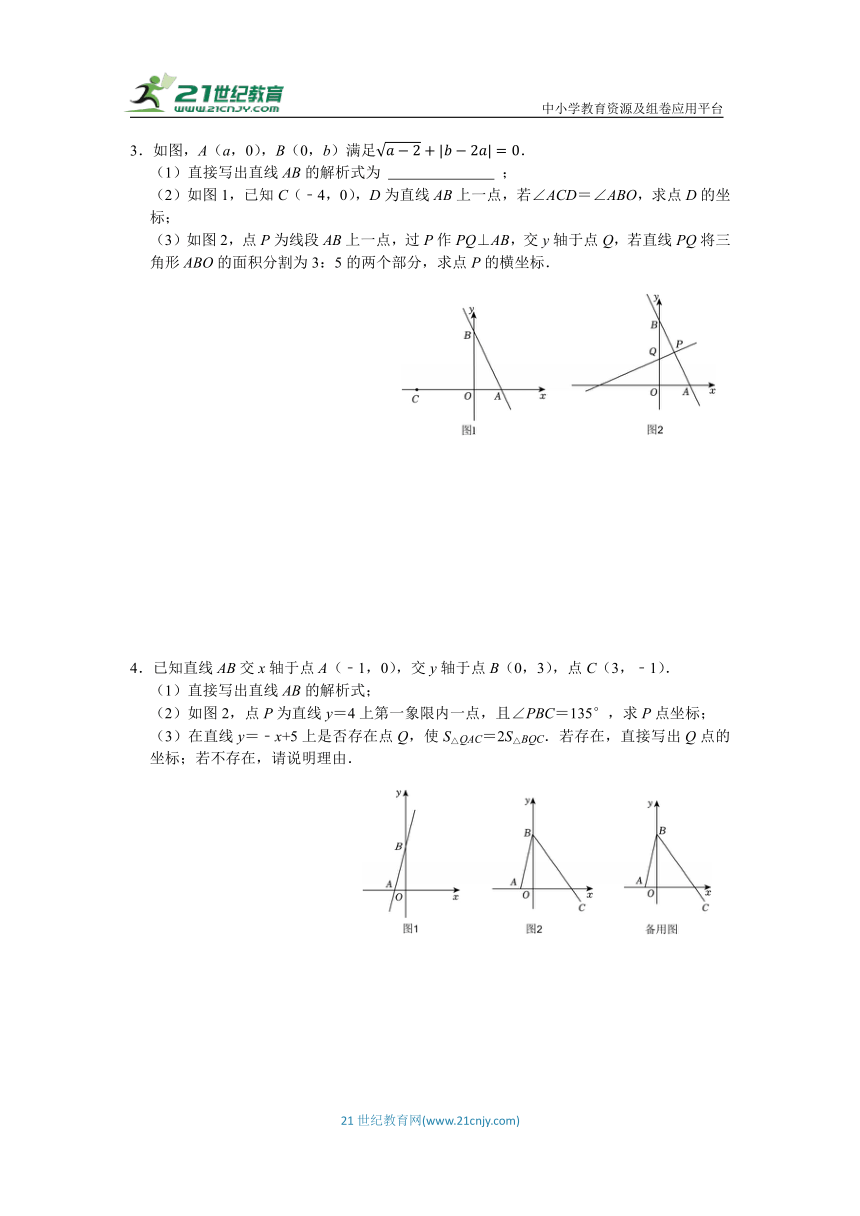
1.如图,在平面直角坐标系中,直线l1的解析式为y=﹣x,直线l2与l1交于点A(﹣a,a),与y轴交于点B(0,b),且(a﹣2)20.
(1)求直线l2的解析式;
(2)若第二象限有一点P(m,8),使得S△AOP=S△AOB,请求出点P的坐标;
(3)线段OA上是否存在一个点M,使得∠ABO+∠MBO=45°?若存在,求出点M的坐标;若不存在,请说明理由.
2.如图1,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①若△PQB的面积为,求点M的坐标;
②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.
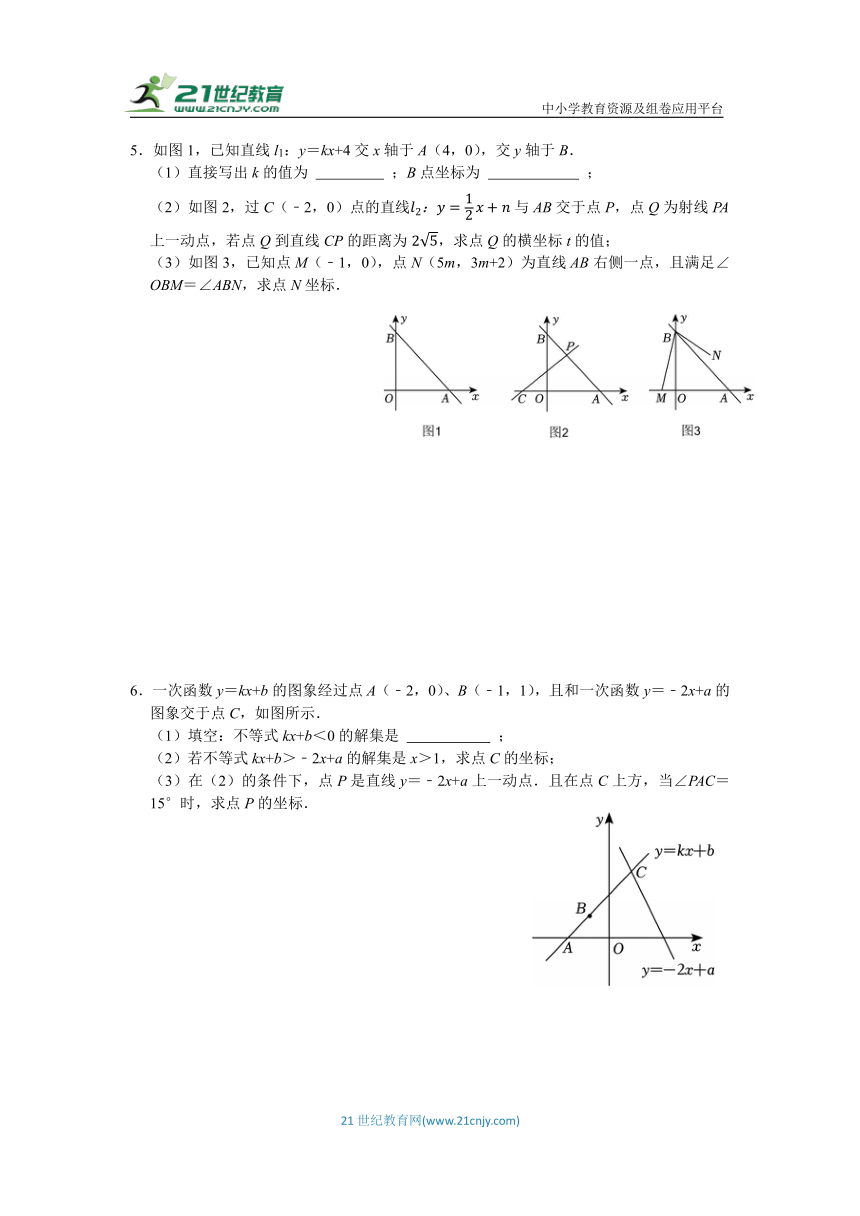
3.如图,A(a,0),B(0,b)满足.
(1)直接写出直线AB的解析式为 ;
(2)如图1,已知C(﹣4,0),D为直线AB上一点,若∠ACD=∠ABO,求点D的坐标;
(3)如图2,点P为线段AB上一点,过P作PQ⊥AB,交y轴于点Q,若直线PQ将三角形ABO的面积分割为3:5的两个部分,求点P的横坐标.
4.已知直线AB交x轴于点A(﹣1,0),交y轴于点B(0,3),点C(3,﹣1).
(1)直接写出直线AB的解析式;
(2)如图2,点P为直线y=4上第一象限内一点,且∠PBC=135°,求P点坐标;
(3)在直线y=﹣x+5上是否存在点Q,使S△QAC=2S△BQC.若存在,直接写出Q点的坐标;若不存在,请说明理由.
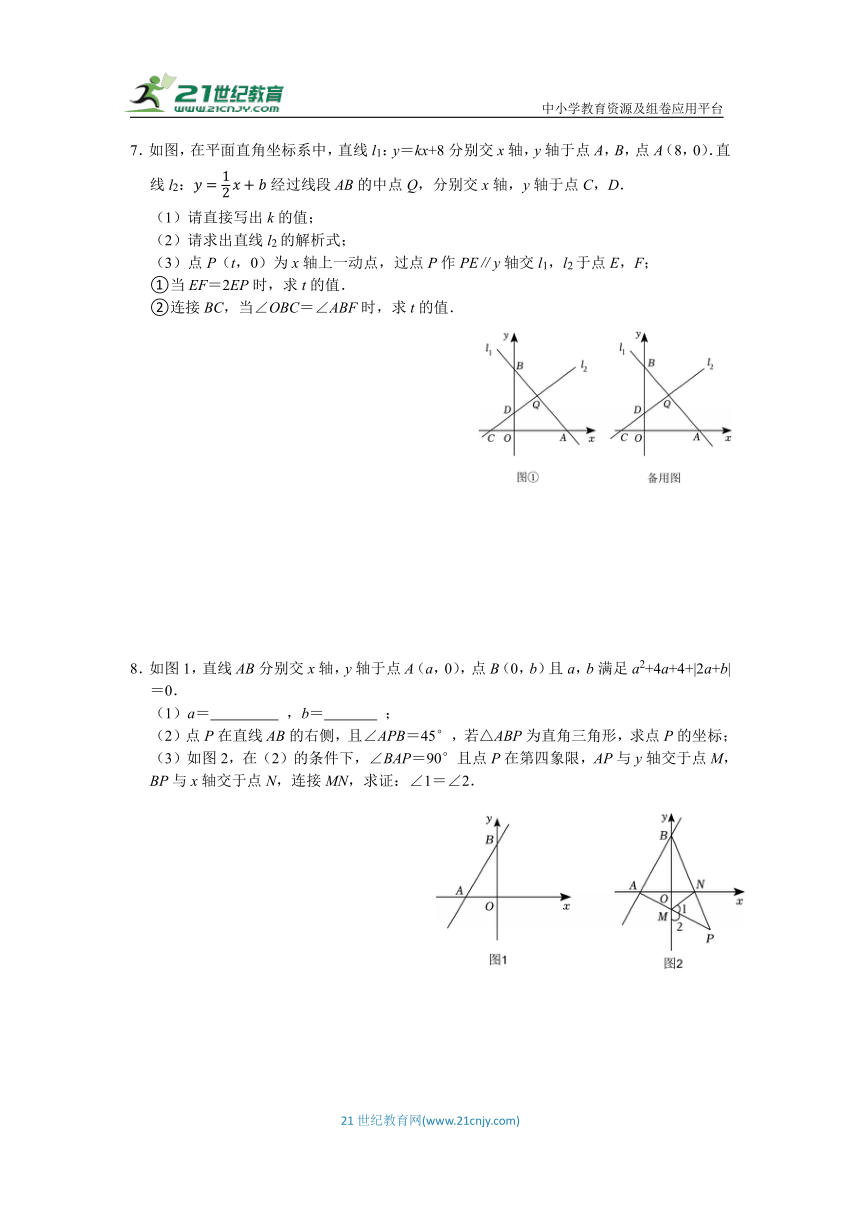
5.如图1,已知直线l1:y=kx+4交x轴于A(4,0),交y轴于B.
(1)直接写出k的值为 ;B点坐标为 ;
(2)如图2,过C(﹣2,0)点的直线与AB交于点P,点Q为射线PA上一动点,若点Q到直线CP的距离为,求点Q的横坐标t的值;
(3)如图3,已知点M(﹣1,0),点N(5m,3m+2)为直线AB右侧一点,且满足∠OBM=∠ABN,求点N坐标.
6.一次函数y=kx+b的图象经过点A(﹣2,0)、B(﹣1,1),且和一次函数y=﹣2x+a的图象交于点C,如图所示.
(1)填空:不等式kx+b<0的解集是 ;
(2)若不等式kx+b>﹣2x+a的解集是x>1,求点C的坐标;
(3)在(2)的条件下,点P是直线y=﹣2x+a上一动点.且在点C上方,当∠PAC=15°时,求点P的坐标.
7.如图,在平面直角坐标系中,直线l1:y=kx+8分别交x轴,y轴于点A,B,点A(8,0).直线l2:经过线段AB的中点Q,分别交x轴,y轴于点C,D.
(1)请直接写出k的值;
(2)请求出直线l2的解析式;
(3)点P(t,0)为x轴上一动点,过点P作PE∥y轴交l1,l2于点E,F;
①当EF=2EP时,求t的值.
②连接BC,当∠OBC=∠ABF时,求t的值.
8.如图1,直线AB分别交x轴,y轴于点A(a,0),点B(0,b)且a,b满足a2+4a+4+|2a+b|=0.
(1)a= ,b= ;
(2)点P在直线AB的右侧,且∠APB=45°,若△ABP为直角三角形,求点P的坐标;
(3)如图2,在(2)的条件下,∠BAP=90°且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接MN,求证:∠1=∠2.
9.如图,直线l1:y=x﹣4与x轴交于点A,与y轴交于点B,直线l2:y=kx+b与x轴交于点C(1,0),与y轴交于点D(0,2),直线l1,l2交于点E.
(1)求直线l2的函数表达式;
(2)试说明CD=CE.
(3)若P为直线l1上一点,当∠POB=∠BDE时,求点P的坐标.
10.如图,直线y=﹣x+m与x轴交于点B(4,0),与y轴交于点A,点C为线段OB上一点,点M为线段AB上一点,OM交AC于N,S△ABC=4.
(1)求直线AB和直线AC的解析式;
(2)若S△ONC=1,求点M的坐标;
(3)若S△AMN=S△ONC,求点M的坐标.
(4)若P是射线CB上一点,且∠CAP=45°,求P点坐标.
11.如图,直线y=kx+b交两轴于点A(4,0),B(0,3).
(1)求直线y=kx+b的解析式;
(2)过A点的直线AQ交y轴负半轴于点Q,若∠BAQ=45°,求点Q的坐标;
(3)在线段AB上找一点D,x轴上找一点E,使BE+DE最小,简要说明点D、E的找法(不需说明理由),并求出此时点E的坐标.
12.如图,直线y=x+9与直线y=﹣2x﹣3交于点C,它们与y轴分别交于A、B两点.
(1)求A、B、C三点的坐标;
(2)点F在x轴上,使S△BFC=10,求点F的坐标;
(3)点P在x轴上,使∠PBO+∠PAO=90°,直接写出点P的坐标.
13.直线l:yx﹣1分别交x轴,y轴于A,B两点,
(1)求线段AB的长;
(2)如图,将l沿x轴正方向平移,分别交x轴,y轴于E,F两点,若直线EF上存在两点C,D,使四边形ABCD为正方形,求此时E点坐标和直线AD的解析式;
(3)在(2)的条件下,将EF绕E点旋转,交直线l于P点,若∠OAB+∠OEP=45°,求P点的坐标.
14.如图,直线y=x+7与直线y=﹣2x﹣2交于点C,它们与y轴分别交于A、B两点.
(1)求A、B、C三点的坐标;
(2)点F在x轴正半轴上,使S△ABC=S△AFC,求点F的坐标;
(3)点P在x轴上,使∠PBO=2∠PAO,直接写出点P的坐标.
15.已知在平面直角坐标系中,A(a、o)、B(o、b)满足|a﹣3|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)求a、b的值.
(2)当P点运动时,PE的值是否发生变化?若变化,说明理由;若不变,请求PE的值.
(3)若∠OPD=45°,求点D的坐标.
参考答案
1.【解答】解:(1)∵(a﹣2)20,
∴a﹣2=0,b﹣6=0,
∴a=2,b=6,
∴A(﹣2,2),B(0,6),
设直线l2的解析式为y=kx+n,则,
解得:,
∴直线l2的解析式为y=2x+6;
(2)作点B关于x轴的对称点B′(0,﹣6),
∵S△AOP=S△AOB,
∴点P在经过点B或B′与OA平行的直线上,
∵A(﹣2,2),
∴直线OA的解析式为y=﹣x,
过点B作OA的平行线BP,则BP的解析式为y=﹣x+c,
把B(0,6)代入得:c=6,
∴BP的解析式为y=﹣x+6,
把P(m,8)代入得:8=﹣m+6,
解得:m=﹣2,
∴P(﹣2,8);
同理可得直线B′P′的解析式为y=﹣x﹣6,
把P(m,8)代入得:8=﹣m﹣6,
解得:m=﹣14,
∴P′(﹣14,8);
综上所述,当S△AOP=S△AOB时,点P的坐标为(﹣2,8)或(﹣14,8);
(3)存在.理由如下:
由(1)知直线AB的解析式为y=2x+6,
当y=0时,2x+6=0,
解得x=﹣3,
∴直线AB交x轴于点H(﹣3,0),
作点H关于y轴的对称点H′(3,0),连接BH′,以BH′为直角边向BH′下方作等腰直角三角形BEH′,使∠BH′E=90°,过点E作EF⊥x轴等于F,如图,
∵△BEH′是等腰直角三角形,
∴BH′=EH′,∠BOH′=∠EFH′=90°,∠EBH′=∠H′BO+∠MBO=45°,
∴∠ABO+∠MBO=∠H′BO+∠MBO=45°,
∵∠H′BO+∠BH′O=90°,∠EH′F+∠BH′O=90°,
∴∠H′BO=∠EH′F,
在△BH′O和△H′EF中,
,
∴△BH′O≌△H′EF(AAS),
∴EF=OH′=3,FH′=OB=6,
∴OF=FH′﹣OH′=6﹣3=3,
∴E(﹣3,﹣3),
设直线BE的解析式为y=k1x+b1,则,
解得,
∴直线BE的解析式为y=3x+6,
同理可得直线OA的解析式为y=﹣x,
联立得,
解得,
∴M(,).
2.【解答】解:(1)在中,令x=0得y=2,
∴B(0,2),
令y=0得x=﹣4,
∴A(﹣4,0),
∵点C与点A关于y轴对称,
∴C(4,0),
设直线BC的解析式为y=kx+b,
∴,
解得,
∴直线BC的函数解析式为yx+2;
(2)①设M(m,0),
∵PQ⊥x轴,
∴P(m,m+2),Q(m,m+2),
∴PQ=|m+2m﹣2|=|m|,
∴S△PQB|m|×|m|,
解得m=±,
∴M的坐标为(,0)或(,0);
②∵点M在线段AC上运动,
∴﹣4≤m≤4,
当点M在线段AO上时,如图:
∵点C与点A关于y轴对称,
∴AB=BC,
∴∠BAC=∠BCA,
∵∠BMP=∠BAC,
∴∠BMP=∠BCA,
∵∠BMP+∠BMC=90°,
∴∠BMC+∠BCA=90°,
∴∠MBC=90°,
∴BM2+BC2=MC2,
∴MC2=(4﹣m)2,BM2=m2+4,BC2=20,
∴m2+4+20=(4﹣m)2,
解得m=﹣1,
∴P(﹣1,);
当点M在线段OC上时,如图:
同理可得P(1,),
综上所述:点P的坐标为(﹣1,)或(1,).
3.【解答】解:(1)∵,则a=2,b=2a=4,
即点A、B的坐标分别为:(2,0)、(0,4),
设直线AB的表达式为:y=kx+4,
将点A的坐标代入上式得:0=2k+4,则k=﹣2,
则AB的表达式为:y=﹣2x+4,
故答案为:y=﹣2x+4;
(2)设直线CD交x轴于点H,
∵∠BOA=∠COH=90°,∠ACD=∠ABO,CO=OB=4,
则△BOA≌△COH(ASA),
则OH=OA=2,则点H(0,2),
由点C、H的坐标得,直线CD的表达式为:yx+2;
(3)∵PQ⊥AB,则∠BPQ=∠BOA=90°,∠QBP=∠OBA,
∴△BPQ∽△BOA,
则(BP:BO)2=S△BPQ:S△BAO=3:8或5:8,
则BD或,
设点D(m,﹣2m+4),而点B(0,4),
则BD2=m2+(﹣2m+4﹣4)2=6或BD2=m2+(﹣2m+4﹣4)2=10,
解得:m或(不合题意的值已舍去).
即点P的横坐标为:或.
4.【解答】解:(1)设直线AB为y=kx+b,而直线AB交x轴于点A(﹣1,0),交y轴于点B(0,3),
∴,
解得:,
∴直线AB为y=3x+3.
(2)设直线BC为y=mx+n,与x轴的交点为Q,
∴,
解得:,
∴直线BC为yx+3,
当yx+3=0,则x,
∴Q(,0),
如图,过B作BG⊥BC于G,交直线y=4于点F,记BC与直线y=4的交点为E,作BP平分∠EBF,交EF与点P,其反向延长线交x轴于H,
∴∠FBP=∠HBC=∠GBH=45°,
∴∠PBC=135°,
过H作HI⊥BG于I,作HJ⊥BC于J,
∴HI=HJ,
∴,
设G(x,0),
由勾股定理,OG2+OB2+OB2+OQ2=GQ2
∴x2+32+32+()2=(x)2,
解得:x=﹣4,
∴G(﹣4,0),
∴BG5,BQ,
∴,而GQ=4,
∴GHGQ,
∴OH=4,
∴H(,0),
同理可得:HP为:y=7x+3,
当y=4时,7x+3=4,
∴x,
∴P(,4).
(3)如图,设Q(m,﹣m+5),取AQ的中点N,
∴S△ACN=S△QCN,
∵S△QAC=2S△BQC,
∴S△QCN=S△BQC,
∴当BN∥CQ时满足条件;
∵A(﹣1,0),Q(m,﹣m+5),
∴N(,).
设直线BN为y=ex+3,
∴e+3,
∴e,
设直线CQ为y=k1x+b1,
同理可得k1,
∵BN∥CQ,
∴,
解得:m,经检验符合题意;
∴Q(,);
如图,当BC在CN的上方,即Q在y轴的右侧时,没有满足条件的点Q,
如图,在BC上取B′使B′C=BC,
则S△BCQ=S△B′CQ,
显然,此时没有符合条件的点Q,
如图,当B′N∥CQ时,
S△BCQ=S△B′CQ=S△NCQS△QCA,此时Q符合条件,
同理可得Q(m,﹣m+5),C(3,﹣1),B(0,3),
∴N(,),B′(6,﹣5),
设CQ为y=k2x+b2,
同理可得k2,
设B′N为:y=k3x+b3,
同理可得k3,
∴,
解得:m=33,经检验符合题意,
∴Q(33,﹣28),
综上:Q(,);或Q(33,﹣28).
5.【解答】解:(1)∵直线l1:y=kx+4交x轴于A(4,0),
∴0=4k+4,
∴k=﹣1,
∴y=﹣x+4,当x=0时,y=4,
∴B(0,4);
故答案为:﹣1,(0,4);
(2)∵过C(﹣2,0)点的直线与AB交于点P,
∴,
∴n=1,
∴,
联立,
解得:,
∴P(2,2),
过点P作PE⊥x轴于点E,则:PE=2,
∵C(﹣2,0),
∴OC=2,
∴,
∵点Q为射线PA上一动点,点Q到直线CP的距离为,Q的横坐标为t,
则:Q(t,﹣t+4),
过点Q作QN⊥CP于点N,QM⊥x轴交CP于点M,如图2,
则:,,QM∥PE,∠QNM=90°,
∴∠M=∠CPE,,
∵∠QNM=∠PEC=90°,
∴△PEC∽△MNQ,
∴,即:,
解得:.
(3)在x轴上取一点P(1,0),连接BP,过点P作BP⊥PQ,交BN于点Q,过点Q作QR⊥x于点R,如图3,
则:∠BOP=∠BPQ=∠QRP=90°,
∴∠PBO=∠QPR=90°﹣∠OPB,
∵A(4,0),B(0,4),
∴OA=OB=4,
∴∠OBA=∠OAB=45°,
∵M(﹣1,0),
∴OM=OP=1,
∵BO⊥PM,
∴BM=BP,
∴∠OBP=∠OBM=∠ABN,
∴∠OBP+∠PBA=∠ABN+∠PBA,
即:∠PBQ=∠OBA=45°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ,
又∠BOP=∠QRP=90°,∠PBO=∠QPR,
∴△BOP≌△PRQ,
∴PR=OB=4,RQ=OP=1,
∴OR=5,
∴Q(5,1),
设直线BQ的解析式为:y=ax+b,
则:,
解得:,
∴,
∵N(5m,3m+2)在直线BQ上,
∴,
∴,
∴.
6.【解答】解:(1)∵一次函数y=kx+b的图象与x轴交于点A(﹣2,0),
∴不等式kx+b<0的解集是x<﹣2,
故答案为x<﹣2.
(2)一次函数y=kx+b的图象经过点A(﹣2,0),B(﹣1,1),
∴,
∴,
∴解析式为:y=x+2,
∵一次函数y=kx+b的图象和一次函数y=﹣2x+a的图象交于点C,
且不等式kx+b>﹣2x+a的解集是x>1,
∴结合图象可得,点C的横坐标为1,
当x=1时,y=x+2=1+2=3,
所以点C的坐标为(1,3).
(3)如图,设直线AC与y轴交于点D,直线PA与y轴交于点E,
∵一次函数y=﹣2x+a的图象经过点C(1,3),
∴3=﹣2×1+a,
∴a=5,
∴函数解析式为:y=﹣2x+5,
对于一次函数y=x+2,
当x=0时,y=2,
∴点D的坐标为(0,2),
∴OD=2,
∵OA=2,
∴OA=OD,
∴∠DAO=45°,
又∵∠PAC=15°,
∴∠PAO=∠DAO+∠PAC=45°+15°=60°,
∴∠AEO=30°,
∴AE=2OA=2×2=4,
在Rt△EAO中,由勾股定理得,
OE2,
∴点E的坐标为(0,2),
设直线AE的解析式为:y=mx+n,
把A(﹣2,0),E(0,2)两点坐标代入上式得,
,
∴,
∴解析式为:yx+2,
解方程组得,
∴,
故点P的坐标为(,).
7.【解答】解:(1)∵A(8,0)过直线l1:y=kx+8,
∴0=k×8+8,
解得:k=﹣1,
∴k=﹣1;
(2)∵l1:y=﹣x+8分别交x轴,y轴于点A,B,
∴B(0,8),
∵AB的中点Q,A(8,0),
∴Q()即Q(4,4),
∵l2:yx+b过Q点,
∴44+b,
解得:b=2,
∴l2:yx+2;
(3)∵P(t,0)为x轴上一动点,过点P作PE∥y轴交l1:y=﹣x+8,l2:yx+2于点E,F;
∴E(t,﹣t+8),F(t,t+2),
∴EF,EP,
当EF=2EP时,2,
解得:t=20,或t;
②∵P(t,0)为x轴上一动点,过点P作PE∥y轴交l1:y=﹣x+8,l2:yx+2于点E,F;
∴E(t,﹣t+8),F(t,t+2),
∵A(8,0),B(0,8),
∴OA=OB=8,
∵∠AOB=90°,
∴∠ABO=45°,ABAO=8,
∵l2:yx+2交x轴于C点,
∴C(﹣4,0),
∵B(0,8),
∴OB=2CO,
当∠OBC=∠ABF时,分两种情况:
F在l1上方时,如图:
过A作AM⊥AB交AF延长线于M点,
∴∠BAM=90°,
∴∠MAN=45°,
作MN⊥x轴于N点,则△AMN是等要直角三角形,
∴AN=MN,
∴∠BAM=∠AOB=90°,∠OBC=∠ABF,
∴△BOC∽△BAM,
∴,即,
解得:AM=4,
∴AN=MN=4,
∴AN=OA+AN=8+4=12,
∴N(12,0),M(12,4),
由B(0,8),
设直线BM:y=nx+8,
∴4=12n+8,
解得:n,
∴BM:yx+8,
∵BM:yx+8过点F(t,t+2),
∴t+2t+8,
解得:t=7.2;
F在l1下方时,如图,
若BF交x轴于N点,过N点作NM⊥AB于M点,
同理:∴△BOC∽△BAM,△AMN是等腰直角三角形,
∴,ANAMNM,
∵BM=AB﹣AM=AB﹣MN=8MN,
∴,
解得:MN,
∴AN,
∴ON=AO﹣AN=8,
∴N(,0),
由B(0,8),
设直线BN:y=nx+8,
∴0n+8,
解得:n=﹣3,
∴BN:y=﹣3x+8,
∵BN:y=﹣3x+8过点F(t,t+2),
∴t+2=﹣3t+8,
解得:t,
综上所述:∠OBC=∠ABF时,t=7.2或.
8.【解答】(1)解:∵a2+4a+4+|2a+b|=0,
∴(a+2)2+|2a+b|=0,
∴a+2=0,2a+b=0,
解得a=﹣2,b=4,
故答案为:﹣2,4;
(2)解:∵a=﹣2,b=4,
∴OA=2,OB=4,
①当∠BAP=90°时,过点A作DE⊥x轴,过点B作BD⊥DE交于D点,过点P作PE⊥DE交于E点,
∵∠BAP=90°,
∴∠BAO+∠PAE=90°,
∵∠BAO+∠ABD=90°,
∴∠PAE=∠ABD,
∵∠APB=45°,
∴AB=AP,
∴△ABD≌△PAE(AAS),
∴BD=AE=2,AD=EP=4,
∴P(2,﹣2);
②当∠ABP=90°时,过点B作GH⊥y轴,过点A作AG⊥GH交于G点,过点P作PH⊥GH交于H点,
同理可得△ABG≌△BPH(AAS),
∴AG=BH=4,BG=PH=2,
∴P(2,2);
综上所述:P点坐标为(2,﹣2)或(2,2);
(3)证明:由(2)知,P(2,﹣2),
由(1)知A(﹣2,0),B(0,4),
设直线AP的解析式为y=kx+b,
∴,
解得,
∴直线AP的解析式为yx﹣1,
∴M(0,﹣1),
同理可得直线BP的解析式为y=﹣3x+4,
∴N(,0),
过P点作PK⊥y轴交于K点,过点P作PQ⊥MN交于Q点,过点P作PT⊥x轴交于T点,
∴KP=2,OT=2,OM=1,NT,
∵OM=1,ON,
∴MN,
∴S△MNPMN×PQ(1+2)×212,
∴PQ=2,
∴PK=PQ,
∴∠1=∠2.
9.【解答】解:(1)将C(1,0).D(0,2)代入y=kx+b得,
,
解得,
∴直线l2的函数解析式为y=﹣2x+2;
(2)当﹣2x+2=x﹣4时,
∴x=2,
∴E(2,﹣2),
过点E作EF⊥x轴于F,
∴EF=OD=2,
∵∠ODC=∠CEF,∠DCO=∠ECF,
∴△DOC≌△EFC(AAS),
∴CD=CE;
(3)∵∠POB=∠BDE,
∴点P在l1上有两个位置,
当点P在点B上方时,如图,
∴OP∥DE,
∴直线OP的函数解析式为y=﹣2x,
∴﹣2x=x﹣4,
∴x,
当x时,y,
∴P(,),
当点P在点B的下方时,设点P关于y轴的对称点为Q,连接OQ交l1为点P',
∴Q(,),
则直线OQ的函数解析式为y=2x,
∴直线OQ与l1的交点为P'(﹣4,﹣8),
综上所述:P(,)或(﹣4,﹣8).
10.【解答】解:(1)把B(4,0)代入y=﹣x+m得﹣4+m=0,解得m=4,
所以直线AB的解析式为y=﹣x+4,
当x=0时,y=﹣x+4=4,则A(0,4),
∵S△ABC=4,
∴BC 4=4,解得BC=2,则C(2,0),
设直线AC的解析式为y=kx+b,
把A(0,4),C(2,0)分别代入得,解得,
∴直线AC的解析式为y=﹣2x+4;
(2)设(t,﹣2t+4),
∵S△ONC=1,
∴2 (﹣2t+4)=1,解得t,
∴N(,1),
设直线ON的解析式为y=px,
把N(,1)代入得p=1,解得p,即直线ON的解析式为yx,
解方程组得,
∴M点坐标为(,);
(3)∵S△AMN=S△ONC,
∴S△ABC=S△OMB=4,
设M(x,﹣x+4),
∴4 (﹣x+4)=4,解得x=2,
∴M点坐标为(2,2);
(4)过B作BH⊥AP于H,A(0,4),点B(4,0),
∴OA=OB=4,
∵∠AOB=90°,
∴∠OAB=45°,AB4,
∵C(2,0),
∴OC=2,
∴AC2,
∵∠CAP=45°,
∴∠OAC=∠BAP,
∵∠AHB=∠AOC=90°,
∴△AOC∽△AHB,
∴,
∴
∴BH,AH,
∵∠PHB=∠AOP=90°,∠BPH=∠APO,
∴△BPH∽△APO,
∴,
∴,
∴PB=8,
∴OP=12,
∴P(12,0).
11.【解答】解:(1)将点A(4,0),B(0,3)代入y=kx+b,
∴,
∴,
∴yx+3;
(2)过点Q作QM⊥AB交于M,
∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=5,
设Q(0,a),
∴BQ=3﹣a,
∴S△ABQ5×QM4×(3﹣a),
∴QM(3﹣a),
∵∠BAQ=45°,
∴QM=AM,
∴AQ2=2AM2
∴16+a2,
解得a=28或a,
∵a<0,
∴a,
∴Q(0,);
(3)作B点关于x轴的对称点B',过B'作B'D⊥AB交于D,交x轴于点E,连接BE,
由对称性可知BE=B'E,
∴BE+DE=B'E+DE≥B'D,此时BE+DE的值最小,
∵B(0,3),
∴B'(0,﹣3),
∴BB'=6,
连接OD,
∴OD=BO=3,
设D(t,t+3),
∴3,
解得t=0(舍)或t,
∴D(,),
设直线B'D的解析式为y=kx+b,
∴,
解得,
∴yx﹣3,
当y=0时,x,
∴E(,0).
12.【解答】解:(1)在y=x+9中,令x=0得y=9,
∴A(0,9),
在y=﹣2x﹣3中,令x=0得y=﹣3,
∴B(0,﹣3),
由得,
∴C(﹣4,5),
答:A的坐标(0,9),B的坐标(0,﹣3),C的坐标(﹣4,5);
(2)设BC交x轴于K,如图:
在y=﹣2x﹣3中,令y=0得x,
∴K(,0),
∵S△BFC=10,
∴S△CKF+S△BKF=10,
∴5 KF3 KF=10,
解得KF,
当F在K右侧时,F(1,0),
当F在K左侧时,F(﹣4,0),
答:点F的坐标为(1,0)或(﹣4,0);
(3)如图:
∵∠PBO+∠PAO=90°,
∴∠APB=90°,
∴AP2+BP2=AB2,
设P(t,0),又A(0,9),B(0,﹣3),
∴(t2+92)+(t2+32)=(9+3)2,
解得t=3或t=﹣3,
∴P(3,0)或(﹣3,0).
13.【解答】解:(1)令x=0,则y=﹣1,B(0,﹣1),
令y=0,则x=2,
∴A(2,0),
∴AB.
(2)过点C作CG⊥OF于G,
∵∠ABC=∠CGB=∠AOB=90°,
∴∠CBG=∠BAO,
∵AB=BC,
∴△AOB≌△BGC(AAS),
∴CG=OB=1,BG=OA=2,
∴C(1,﹣3),
过点D作DH⊥AE于H,
同理可得,D(3,﹣2),
设EF:y=kx+b,
将C(1,﹣3),D(3,﹣2)代入y=kx+b中,得,
解得:,
∴直线EF的解析式为yx.令y=0,则yx0,
解得:x=7,
∴E(7,0),
设直线AD的解析式为y=k'x+b',
∵A(2,0),D(3,﹣2),
∴,
∴,
∴直线AD的解析式为y=﹣2x+4,
(3)①当P在x轴上方时,设P(t,t﹣1),
过点E作EQ⊥EP交AP于Q,
∴∠OAB=∠PAE,∠OAB+∠OEP=45°,
∴∠EPQ=45°,过点P作PG⊥x轴于G,过点Q作QH⊥x轴于H,
∴PE=EQ,
∵∠PGE=∠QHE=90°,∠PEG=∠EQH,
∴△PEG≌△EQH(AAS),
∴PG=EH,EG=QH=7﹣t,
∴OH=OE+EH=7,
∴Q(t+6,7﹣t),
将Q(t+6,7﹣t),代入yx﹣1中,
得(t+6)﹣1=7﹣t,
解得t=4,
∴P(4,1).
②当P在x轴下方时,可得点P关于x轴的对称点为N(4,﹣1),
求得直线EN的解析式为y,
∴,
解得:.
∴P(﹣8,﹣5).
综合以上可得点P的坐标为P(4,1)或(﹣8,﹣5).
14.【解答】解:(1)对于y=x+7,令x=0,则y=7,
故点A(0,7),
同理可得,点B(0,﹣2),
联立y=x+7和y=﹣2x﹣2并解得,
故点C(﹣3,4);
(2)过点B作AC的平行线交x轴于点F,则点F为所求点,
理由:∵BF∥AC,
故△ABC和△AFC等高,故S△ABC=S△AFC,
设直线BF的表达式为y=x+t,
上述直线过点B,故t=﹣2,
故直线BF的表达式为y=x﹣2,
令y=x﹣2=0,解得x=2,
故点F(2,0);
(3)在y轴的正半轴上取点B′(0,2),则OB=OB′=2,连接PB′,
∴PB=PB′,则∠PBO=∠PB′O=2∠PAO,
∴∠B′AP=∠B′PA,
故PB′=B′A=7﹣2=5,
设点P(x,0),
则PB′2=22+x2=52,解得x,
故点P的坐标为(,0)或(,0).
15.【解答】解:(1)∵|a﹣3|=0,
∴,
解得:a=b=3;
(2)当P点运动时,PE的值不变化,PE=3,理由为:
过O作OC⊥AB,
∵OA=OB=3,C为斜边AB的中点,
∴AB6,即OCAB=3,
∵△AOB为等腰直角三角形,
∴AC=BC,∠AOC=∠BOC=45°,
∵PO=PD,
∴∠POD=∠PDO,
∵∠POD=45°+∠POC,∠PDO=45°+∠APD,
∴∠POC=∠APD,
在△POC和△DPE中,
,
∴△POC≌△DPE(AAS),
∴OC=PE=3;
(3)∵OP=DP,∠OPD=45°,
∴∠POD=∠PDO67.5°,
∴∠PDA=180°﹣∠PDO=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°﹣45°=22.5°,
∴∠BPO=180°﹣∠OPD﹣∠APD=112.5°,
∴∠PDA=∠BPO,
在△POB和△DPA中,
,
∴△POB≌△DPA(AAS),
∴OB=PA=OA=3,
∴DA=PB=6﹣3,
∴OD=OA﹣DA=3(6﹣3)=66,
则D(66,0).
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练一次函数中角度相关问题训练
1.如图,在平面直角坐标系中,直线l1的解析式为y=﹣x,直线l2与l1交于点A(﹣a,a),与y轴交于点B(0,b),且(a﹣2)20.
(1)求直线l2的解析式;
(2)若第二象限有一点P(m,8),使得S△AOP=S△AOB,请求出点P的坐标;
(3)线段OA上是否存在一个点M,使得∠ABO+∠MBO=45°?若存在,求出点M的坐标;若不存在,请说明理由.
2.如图1,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①若△PQB的面积为,求点M的坐标;
②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.
3.如图,A(a,0),B(0,b)满足.
(1)直接写出直线AB的解析式为 ;
(2)如图1,已知C(﹣4,0),D为直线AB上一点,若∠ACD=∠ABO,求点D的坐标;
(3)如图2,点P为线段AB上一点,过P作PQ⊥AB,交y轴于点Q,若直线PQ将三角形ABO的面积分割为3:5的两个部分,求点P的横坐标.
4.已知直线AB交x轴于点A(﹣1,0),交y轴于点B(0,3),点C(3,﹣1).
(1)直接写出直线AB的解析式;
(2)如图2,点P为直线y=4上第一象限内一点,且∠PBC=135°,求P点坐标;
(3)在直线y=﹣x+5上是否存在点Q,使S△QAC=2S△BQC.若存在,直接写出Q点的坐标;若不存在,请说明理由.
5.如图1,已知直线l1:y=kx+4交x轴于A(4,0),交y轴于B.
(1)直接写出k的值为 ;B点坐标为 ;
(2)如图2,过C(﹣2,0)点的直线与AB交于点P,点Q为射线PA上一动点,若点Q到直线CP的距离为,求点Q的横坐标t的值;
(3)如图3,已知点M(﹣1,0),点N(5m,3m+2)为直线AB右侧一点,且满足∠OBM=∠ABN,求点N坐标.
6.一次函数y=kx+b的图象经过点A(﹣2,0)、B(﹣1,1),且和一次函数y=﹣2x+a的图象交于点C,如图所示.
(1)填空:不等式kx+b<0的解集是 ;
(2)若不等式kx+b>﹣2x+a的解集是x>1,求点C的坐标;
(3)在(2)的条件下,点P是直线y=﹣2x+a上一动点.且在点C上方,当∠PAC=15°时,求点P的坐标.
7.如图,在平面直角坐标系中,直线l1:y=kx+8分别交x轴,y轴于点A,B,点A(8,0).直线l2:经过线段AB的中点Q,分别交x轴,y轴于点C,D.
(1)请直接写出k的值;
(2)请求出直线l2的解析式;
(3)点P(t,0)为x轴上一动点,过点P作PE∥y轴交l1,l2于点E,F;
①当EF=2EP时,求t的值.
②连接BC,当∠OBC=∠ABF时,求t的值.
8.如图1,直线AB分别交x轴,y轴于点A(a,0),点B(0,b)且a,b满足a2+4a+4+|2a+b|=0.
(1)a= ,b= ;
(2)点P在直线AB的右侧,且∠APB=45°,若△ABP为直角三角形,求点P的坐标;
(3)如图2,在(2)的条件下,∠BAP=90°且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接MN,求证:∠1=∠2.
9.如图,直线l1:y=x﹣4与x轴交于点A,与y轴交于点B,直线l2:y=kx+b与x轴交于点C(1,0),与y轴交于点D(0,2),直线l1,l2交于点E.
(1)求直线l2的函数表达式;
(2)试说明CD=CE.
(3)若P为直线l1上一点,当∠POB=∠BDE时,求点P的坐标.
10.如图,直线y=﹣x+m与x轴交于点B(4,0),与y轴交于点A,点C为线段OB上一点,点M为线段AB上一点,OM交AC于N,S△ABC=4.
(1)求直线AB和直线AC的解析式;
(2)若S△ONC=1,求点M的坐标;
(3)若S△AMN=S△ONC,求点M的坐标.
(4)若P是射线CB上一点,且∠CAP=45°,求P点坐标.
11.如图,直线y=kx+b交两轴于点A(4,0),B(0,3).
(1)求直线y=kx+b的解析式;
(2)过A点的直线AQ交y轴负半轴于点Q,若∠BAQ=45°,求点Q的坐标;
(3)在线段AB上找一点D,x轴上找一点E,使BE+DE最小,简要说明点D、E的找法(不需说明理由),并求出此时点E的坐标.
12.如图,直线y=x+9与直线y=﹣2x﹣3交于点C,它们与y轴分别交于A、B两点.
(1)求A、B、C三点的坐标;
(2)点F在x轴上,使S△BFC=10,求点F的坐标;
(3)点P在x轴上,使∠PBO+∠PAO=90°,直接写出点P的坐标.
13.直线l:yx﹣1分别交x轴,y轴于A,B两点,
(1)求线段AB的长;
(2)如图,将l沿x轴正方向平移,分别交x轴,y轴于E,F两点,若直线EF上存在两点C,D,使四边形ABCD为正方形,求此时E点坐标和直线AD的解析式;
(3)在(2)的条件下,将EF绕E点旋转,交直线l于P点,若∠OAB+∠OEP=45°,求P点的坐标.
14.如图,直线y=x+7与直线y=﹣2x﹣2交于点C,它们与y轴分别交于A、B两点.
(1)求A、B、C三点的坐标;
(2)点F在x轴正半轴上,使S△ABC=S△AFC,求点F的坐标;
(3)点P在x轴上,使∠PBO=2∠PAO,直接写出点P的坐标.
15.已知在平面直角坐标系中,A(a、o)、B(o、b)满足|a﹣3|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)求a、b的值.
(2)当P点运动时,PE的值是否发生变化?若变化,说明理由;若不变,请求PE的值.
(3)若∠OPD=45°,求点D的坐标.
参考答案
1.【解答】解:(1)∵(a﹣2)20,
∴a﹣2=0,b﹣6=0,
∴a=2,b=6,
∴A(﹣2,2),B(0,6),
设直线l2的解析式为y=kx+n,则,
解得:,
∴直线l2的解析式为y=2x+6;
(2)作点B关于x轴的对称点B′(0,﹣6),
∵S△AOP=S△AOB,
∴点P在经过点B或B′与OA平行的直线上,
∵A(﹣2,2),
∴直线OA的解析式为y=﹣x,
过点B作OA的平行线BP,则BP的解析式为y=﹣x+c,
把B(0,6)代入得:c=6,
∴BP的解析式为y=﹣x+6,
把P(m,8)代入得:8=﹣m+6,
解得:m=﹣2,
∴P(﹣2,8);
同理可得直线B′P′的解析式为y=﹣x﹣6,
把P(m,8)代入得:8=﹣m﹣6,
解得:m=﹣14,
∴P′(﹣14,8);
综上所述,当S△AOP=S△AOB时,点P的坐标为(﹣2,8)或(﹣14,8);
(3)存在.理由如下:
由(1)知直线AB的解析式为y=2x+6,
当y=0时,2x+6=0,
解得x=﹣3,
∴直线AB交x轴于点H(﹣3,0),
作点H关于y轴的对称点H′(3,0),连接BH′,以BH′为直角边向BH′下方作等腰直角三角形BEH′,使∠BH′E=90°,过点E作EF⊥x轴等于F,如图,
∵△BEH′是等腰直角三角形,
∴BH′=EH′,∠BOH′=∠EFH′=90°,∠EBH′=∠H′BO+∠MBO=45°,
∴∠ABO+∠MBO=∠H′BO+∠MBO=45°,
∵∠H′BO+∠BH′O=90°,∠EH′F+∠BH′O=90°,
∴∠H′BO=∠EH′F,
在△BH′O和△H′EF中,
,
∴△BH′O≌△H′EF(AAS),
∴EF=OH′=3,FH′=OB=6,
∴OF=FH′﹣OH′=6﹣3=3,
∴E(﹣3,﹣3),
设直线BE的解析式为y=k1x+b1,则,
解得,
∴直线BE的解析式为y=3x+6,
同理可得直线OA的解析式为y=﹣x,
联立得,
解得,
∴M(,).
2.【解答】解:(1)在中,令x=0得y=2,
∴B(0,2),
令y=0得x=﹣4,
∴A(﹣4,0),
∵点C与点A关于y轴对称,
∴C(4,0),
设直线BC的解析式为y=kx+b,
∴,
解得,
∴直线BC的函数解析式为yx+2;
(2)①设M(m,0),
∵PQ⊥x轴,
∴P(m,m+2),Q(m,m+2),
∴PQ=|m+2m﹣2|=|m|,
∴S△PQB|m|×|m|,
解得m=±,
∴M的坐标为(,0)或(,0);
②∵点M在线段AC上运动,
∴﹣4≤m≤4,
当点M在线段AO上时,如图:
∵点C与点A关于y轴对称,
∴AB=BC,
∴∠BAC=∠BCA,
∵∠BMP=∠BAC,
∴∠BMP=∠BCA,
∵∠BMP+∠BMC=90°,
∴∠BMC+∠BCA=90°,
∴∠MBC=90°,
∴BM2+BC2=MC2,
∴MC2=(4﹣m)2,BM2=m2+4,BC2=20,
∴m2+4+20=(4﹣m)2,
解得m=﹣1,
∴P(﹣1,);
当点M在线段OC上时,如图:
同理可得P(1,),
综上所述:点P的坐标为(﹣1,)或(1,).
3.【解答】解:(1)∵,则a=2,b=2a=4,
即点A、B的坐标分别为:(2,0)、(0,4),
设直线AB的表达式为:y=kx+4,
将点A的坐标代入上式得:0=2k+4,则k=﹣2,
则AB的表达式为:y=﹣2x+4,
故答案为:y=﹣2x+4;
(2)设直线CD交x轴于点H,
∵∠BOA=∠COH=90°,∠ACD=∠ABO,CO=OB=4,
则△BOA≌△COH(ASA),
则OH=OA=2,则点H(0,2),
由点C、H的坐标得,直线CD的表达式为:yx+2;
(3)∵PQ⊥AB,则∠BPQ=∠BOA=90°,∠QBP=∠OBA,
∴△BPQ∽△BOA,
则(BP:BO)2=S△BPQ:S△BAO=3:8或5:8,
则BD或,
设点D(m,﹣2m+4),而点B(0,4),
则BD2=m2+(﹣2m+4﹣4)2=6或BD2=m2+(﹣2m+4﹣4)2=10,
解得:m或(不合题意的值已舍去).
即点P的横坐标为:或.
4.【解答】解:(1)设直线AB为y=kx+b,而直线AB交x轴于点A(﹣1,0),交y轴于点B(0,3),
∴,
解得:,
∴直线AB为y=3x+3.
(2)设直线BC为y=mx+n,与x轴的交点为Q,
∴,
解得:,
∴直线BC为yx+3,
当yx+3=0,则x,
∴Q(,0),
如图,过B作BG⊥BC于G,交直线y=4于点F,记BC与直线y=4的交点为E,作BP平分∠EBF,交EF与点P,其反向延长线交x轴于H,
∴∠FBP=∠HBC=∠GBH=45°,
∴∠PBC=135°,
过H作HI⊥BG于I,作HJ⊥BC于J,
∴HI=HJ,
∴,
设G(x,0),
由勾股定理,OG2+OB2+OB2+OQ2=GQ2
∴x2+32+32+()2=(x)2,
解得:x=﹣4,
∴G(﹣4,0),
∴BG5,BQ,
∴,而GQ=4,
∴GHGQ,
∴OH=4,
∴H(,0),
同理可得:HP为:y=7x+3,
当y=4时,7x+3=4,
∴x,
∴P(,4).
(3)如图,设Q(m,﹣m+5),取AQ的中点N,
∴S△ACN=S△QCN,
∵S△QAC=2S△BQC,
∴S△QCN=S△BQC,
∴当BN∥CQ时满足条件;
∵A(﹣1,0),Q(m,﹣m+5),
∴N(,).
设直线BN为y=ex+3,
∴e+3,
∴e,
设直线CQ为y=k1x+b1,
同理可得k1,
∵BN∥CQ,
∴,
解得:m,经检验符合题意;
∴Q(,);
如图,当BC在CN的上方,即Q在y轴的右侧时,没有满足条件的点Q,
如图,在BC上取B′使B′C=BC,
则S△BCQ=S△B′CQ,
显然,此时没有符合条件的点Q,
如图,当B′N∥CQ时,
S△BCQ=S△B′CQ=S△NCQS△QCA,此时Q符合条件,
同理可得Q(m,﹣m+5),C(3,﹣1),B(0,3),
∴N(,),B′(6,﹣5),
设CQ为y=k2x+b2,
同理可得k2,
设B′N为:y=k3x+b3,
同理可得k3,
∴,
解得:m=33,经检验符合题意,
∴Q(33,﹣28),
综上:Q(,);或Q(33,﹣28).
5.【解答】解:(1)∵直线l1:y=kx+4交x轴于A(4,0),
∴0=4k+4,
∴k=﹣1,
∴y=﹣x+4,当x=0时,y=4,
∴B(0,4);
故答案为:﹣1,(0,4);
(2)∵过C(﹣2,0)点的直线与AB交于点P,
∴,
∴n=1,
∴,
联立,
解得:,
∴P(2,2),
过点P作PE⊥x轴于点E,则:PE=2,
∵C(﹣2,0),
∴OC=2,
∴,
∵点Q为射线PA上一动点,点Q到直线CP的距离为,Q的横坐标为t,
则:Q(t,﹣t+4),
过点Q作QN⊥CP于点N,QM⊥x轴交CP于点M,如图2,
则:,,QM∥PE,∠QNM=90°,
∴∠M=∠CPE,,
∵∠QNM=∠PEC=90°,
∴△PEC∽△MNQ,
∴,即:,
解得:.
(3)在x轴上取一点P(1,0),连接BP,过点P作BP⊥PQ,交BN于点Q,过点Q作QR⊥x于点R,如图3,
则:∠BOP=∠BPQ=∠QRP=90°,
∴∠PBO=∠QPR=90°﹣∠OPB,
∵A(4,0),B(0,4),
∴OA=OB=4,
∴∠OBA=∠OAB=45°,
∵M(﹣1,0),
∴OM=OP=1,
∵BO⊥PM,
∴BM=BP,
∴∠OBP=∠OBM=∠ABN,
∴∠OBP+∠PBA=∠ABN+∠PBA,
即:∠PBQ=∠OBA=45°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ,
又∠BOP=∠QRP=90°,∠PBO=∠QPR,
∴△BOP≌△PRQ,
∴PR=OB=4,RQ=OP=1,
∴OR=5,
∴Q(5,1),
设直线BQ的解析式为:y=ax+b,
则:,
解得:,
∴,
∵N(5m,3m+2)在直线BQ上,
∴,
∴,
∴.
6.【解答】解:(1)∵一次函数y=kx+b的图象与x轴交于点A(﹣2,0),
∴不等式kx+b<0的解集是x<﹣2,
故答案为x<﹣2.
(2)一次函数y=kx+b的图象经过点A(﹣2,0),B(﹣1,1),
∴,
∴,
∴解析式为:y=x+2,
∵一次函数y=kx+b的图象和一次函数y=﹣2x+a的图象交于点C,
且不等式kx+b>﹣2x+a的解集是x>1,
∴结合图象可得,点C的横坐标为1,
当x=1时,y=x+2=1+2=3,
所以点C的坐标为(1,3).
(3)如图,设直线AC与y轴交于点D,直线PA与y轴交于点E,
∵一次函数y=﹣2x+a的图象经过点C(1,3),
∴3=﹣2×1+a,
∴a=5,
∴函数解析式为:y=﹣2x+5,
对于一次函数y=x+2,
当x=0时,y=2,
∴点D的坐标为(0,2),
∴OD=2,
∵OA=2,
∴OA=OD,
∴∠DAO=45°,
又∵∠PAC=15°,
∴∠PAO=∠DAO+∠PAC=45°+15°=60°,
∴∠AEO=30°,
∴AE=2OA=2×2=4,
在Rt△EAO中,由勾股定理得,
OE2,
∴点E的坐标为(0,2),
设直线AE的解析式为:y=mx+n,
把A(﹣2,0),E(0,2)两点坐标代入上式得,
,
∴,
∴解析式为:yx+2,
解方程组得,
∴,
故点P的坐标为(,).
7.【解答】解:(1)∵A(8,0)过直线l1:y=kx+8,
∴0=k×8+8,
解得:k=﹣1,
∴k=﹣1;
(2)∵l1:y=﹣x+8分别交x轴,y轴于点A,B,
∴B(0,8),
∵AB的中点Q,A(8,0),
∴Q()即Q(4,4),
∵l2:yx+b过Q点,
∴44+b,
解得:b=2,
∴l2:yx+2;
(3)∵P(t,0)为x轴上一动点,过点P作PE∥y轴交l1:y=﹣x+8,l2:yx+2于点E,F;
∴E(t,﹣t+8),F(t,t+2),
∴EF,EP,
当EF=2EP时,2,
解得:t=20,或t;
②∵P(t,0)为x轴上一动点,过点P作PE∥y轴交l1:y=﹣x+8,l2:yx+2于点E,F;
∴E(t,﹣t+8),F(t,t+2),
∵A(8,0),B(0,8),
∴OA=OB=8,
∵∠AOB=90°,
∴∠ABO=45°,ABAO=8,
∵l2:yx+2交x轴于C点,
∴C(﹣4,0),
∵B(0,8),
∴OB=2CO,
当∠OBC=∠ABF时,分两种情况:
F在l1上方时,如图:
过A作AM⊥AB交AF延长线于M点,
∴∠BAM=90°,
∴∠MAN=45°,
作MN⊥x轴于N点,则△AMN是等要直角三角形,
∴AN=MN,
∴∠BAM=∠AOB=90°,∠OBC=∠ABF,
∴△BOC∽△BAM,
∴,即,
解得:AM=4,
∴AN=MN=4,
∴AN=OA+AN=8+4=12,
∴N(12,0),M(12,4),
由B(0,8),
设直线BM:y=nx+8,
∴4=12n+8,
解得:n,
∴BM:yx+8,
∵BM:yx+8过点F(t,t+2),
∴t+2t+8,
解得:t=7.2;
F在l1下方时,如图,
若BF交x轴于N点,过N点作NM⊥AB于M点,
同理:∴△BOC∽△BAM,△AMN是等腰直角三角形,
∴,ANAMNM,
∵BM=AB﹣AM=AB﹣MN=8MN,
∴,
解得:MN,
∴AN,
∴ON=AO﹣AN=8,
∴N(,0),
由B(0,8),
设直线BN:y=nx+8,
∴0n+8,
解得:n=﹣3,
∴BN:y=﹣3x+8,
∵BN:y=﹣3x+8过点F(t,t+2),
∴t+2=﹣3t+8,
解得:t,
综上所述:∠OBC=∠ABF时,t=7.2或.
8.【解答】(1)解:∵a2+4a+4+|2a+b|=0,
∴(a+2)2+|2a+b|=0,
∴a+2=0,2a+b=0,
解得a=﹣2,b=4,
故答案为:﹣2,4;
(2)解:∵a=﹣2,b=4,
∴OA=2,OB=4,
①当∠BAP=90°时,过点A作DE⊥x轴,过点B作BD⊥DE交于D点,过点P作PE⊥DE交于E点,
∵∠BAP=90°,
∴∠BAO+∠PAE=90°,
∵∠BAO+∠ABD=90°,
∴∠PAE=∠ABD,
∵∠APB=45°,
∴AB=AP,
∴△ABD≌△PAE(AAS),
∴BD=AE=2,AD=EP=4,
∴P(2,﹣2);
②当∠ABP=90°时,过点B作GH⊥y轴,过点A作AG⊥GH交于G点,过点P作PH⊥GH交于H点,
同理可得△ABG≌△BPH(AAS),
∴AG=BH=4,BG=PH=2,
∴P(2,2);
综上所述:P点坐标为(2,﹣2)或(2,2);
(3)证明:由(2)知,P(2,﹣2),
由(1)知A(﹣2,0),B(0,4),
设直线AP的解析式为y=kx+b,
∴,
解得,
∴直线AP的解析式为yx﹣1,
∴M(0,﹣1),
同理可得直线BP的解析式为y=﹣3x+4,
∴N(,0),
过P点作PK⊥y轴交于K点,过点P作PQ⊥MN交于Q点,过点P作PT⊥x轴交于T点,
∴KP=2,OT=2,OM=1,NT,
∵OM=1,ON,
∴MN,
∴S△MNPMN×PQ(1+2)×212,
∴PQ=2,
∴PK=PQ,
∴∠1=∠2.
9.【解答】解:(1)将C(1,0).D(0,2)代入y=kx+b得,
,
解得,
∴直线l2的函数解析式为y=﹣2x+2;
(2)当﹣2x+2=x﹣4时,
∴x=2,
∴E(2,﹣2),
过点E作EF⊥x轴于F,
∴EF=OD=2,
∵∠ODC=∠CEF,∠DCO=∠ECF,
∴△DOC≌△EFC(AAS),
∴CD=CE;
(3)∵∠POB=∠BDE,
∴点P在l1上有两个位置,
当点P在点B上方时,如图,
∴OP∥DE,
∴直线OP的函数解析式为y=﹣2x,
∴﹣2x=x﹣4,
∴x,
当x时,y,
∴P(,),
当点P在点B的下方时,设点P关于y轴的对称点为Q,连接OQ交l1为点P',
∴Q(,),
则直线OQ的函数解析式为y=2x,
∴直线OQ与l1的交点为P'(﹣4,﹣8),
综上所述:P(,)或(﹣4,﹣8).
10.【解答】解:(1)把B(4,0)代入y=﹣x+m得﹣4+m=0,解得m=4,
所以直线AB的解析式为y=﹣x+4,
当x=0时,y=﹣x+4=4,则A(0,4),
∵S△ABC=4,
∴BC 4=4,解得BC=2,则C(2,0),
设直线AC的解析式为y=kx+b,
把A(0,4),C(2,0)分别代入得,解得,
∴直线AC的解析式为y=﹣2x+4;
(2)设(t,﹣2t+4),
∵S△ONC=1,
∴2 (﹣2t+4)=1,解得t,
∴N(,1),
设直线ON的解析式为y=px,
把N(,1)代入得p=1,解得p,即直线ON的解析式为yx,
解方程组得,
∴M点坐标为(,);
(3)∵S△AMN=S△ONC,
∴S△ABC=S△OMB=4,
设M(x,﹣x+4),
∴4 (﹣x+4)=4,解得x=2,
∴M点坐标为(2,2);
(4)过B作BH⊥AP于H,A(0,4),点B(4,0),
∴OA=OB=4,
∵∠AOB=90°,
∴∠OAB=45°,AB4,
∵C(2,0),
∴OC=2,
∴AC2,
∵∠CAP=45°,
∴∠OAC=∠BAP,
∵∠AHB=∠AOC=90°,
∴△AOC∽△AHB,
∴,
∴
∴BH,AH,
∵∠PHB=∠AOP=90°,∠BPH=∠APO,
∴△BPH∽△APO,
∴,
∴,
∴PB=8,
∴OP=12,
∴P(12,0).
11.【解答】解:(1)将点A(4,0),B(0,3)代入y=kx+b,
∴,
∴,
∴yx+3;
(2)过点Q作QM⊥AB交于M,
∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=5,
设Q(0,a),
∴BQ=3﹣a,
∴S△ABQ5×QM4×(3﹣a),
∴QM(3﹣a),
∵∠BAQ=45°,
∴QM=AM,
∴AQ2=2AM2
∴16+a2,
解得a=28或a,
∵a<0,
∴a,
∴Q(0,);
(3)作B点关于x轴的对称点B',过B'作B'D⊥AB交于D,交x轴于点E,连接BE,
由对称性可知BE=B'E,
∴BE+DE=B'E+DE≥B'D,此时BE+DE的值最小,
∵B(0,3),
∴B'(0,﹣3),
∴BB'=6,
连接OD,
∴OD=BO=3,
设D(t,t+3),
∴3,
解得t=0(舍)或t,
∴D(,),
设直线B'D的解析式为y=kx+b,
∴,
解得,
∴yx﹣3,
当y=0时,x,
∴E(,0).
12.【解答】解:(1)在y=x+9中,令x=0得y=9,
∴A(0,9),
在y=﹣2x﹣3中,令x=0得y=﹣3,
∴B(0,﹣3),
由得,
∴C(﹣4,5),
答:A的坐标(0,9),B的坐标(0,﹣3),C的坐标(﹣4,5);
(2)设BC交x轴于K,如图:
在y=﹣2x﹣3中,令y=0得x,
∴K(,0),
∵S△BFC=10,
∴S△CKF+S△BKF=10,
∴5 KF3 KF=10,
解得KF,
当F在K右侧时,F(1,0),
当F在K左侧时,F(﹣4,0),
答:点F的坐标为(1,0)或(﹣4,0);
(3)如图:
∵∠PBO+∠PAO=90°,
∴∠APB=90°,
∴AP2+BP2=AB2,
设P(t,0),又A(0,9),B(0,﹣3),
∴(t2+92)+(t2+32)=(9+3)2,
解得t=3或t=﹣3,
∴P(3,0)或(﹣3,0).
13.【解答】解:(1)令x=0,则y=﹣1,B(0,﹣1),
令y=0,则x=2,
∴A(2,0),
∴AB.
(2)过点C作CG⊥OF于G,
∵∠ABC=∠CGB=∠AOB=90°,
∴∠CBG=∠BAO,
∵AB=BC,
∴△AOB≌△BGC(AAS),
∴CG=OB=1,BG=OA=2,
∴C(1,﹣3),
过点D作DH⊥AE于H,
同理可得,D(3,﹣2),
设EF:y=kx+b,
将C(1,﹣3),D(3,﹣2)代入y=kx+b中,得,
解得:,
∴直线EF的解析式为yx.令y=0,则yx0,
解得:x=7,
∴E(7,0),
设直线AD的解析式为y=k'x+b',
∵A(2,0),D(3,﹣2),
∴,
∴,
∴直线AD的解析式为y=﹣2x+4,
(3)①当P在x轴上方时,设P(t,t﹣1),
过点E作EQ⊥EP交AP于Q,
∴∠OAB=∠PAE,∠OAB+∠OEP=45°,
∴∠EPQ=45°,过点P作PG⊥x轴于G,过点Q作QH⊥x轴于H,
∴PE=EQ,
∵∠PGE=∠QHE=90°,∠PEG=∠EQH,
∴△PEG≌△EQH(AAS),
∴PG=EH,EG=QH=7﹣t,
∴OH=OE+EH=7,
∴Q(t+6,7﹣t),
将Q(t+6,7﹣t),代入yx﹣1中,
得(t+6)﹣1=7﹣t,
解得t=4,
∴P(4,1).
②当P在x轴下方时,可得点P关于x轴的对称点为N(4,﹣1),
求得直线EN的解析式为y,
∴,
解得:.
∴P(﹣8,﹣5).
综合以上可得点P的坐标为P(4,1)或(﹣8,﹣5).
14.【解答】解:(1)对于y=x+7,令x=0,则y=7,
故点A(0,7),
同理可得,点B(0,﹣2),
联立y=x+7和y=﹣2x﹣2并解得,
故点C(﹣3,4);
(2)过点B作AC的平行线交x轴于点F,则点F为所求点,
理由:∵BF∥AC,
故△ABC和△AFC等高,故S△ABC=S△AFC,
设直线BF的表达式为y=x+t,
上述直线过点B,故t=﹣2,
故直线BF的表达式为y=x﹣2,
令y=x﹣2=0,解得x=2,
故点F(2,0);
(3)在y轴的正半轴上取点B′(0,2),则OB=OB′=2,连接PB′,
∴PB=PB′,则∠PBO=∠PB′O=2∠PAO,
∴∠B′AP=∠B′PA,
故PB′=B′A=7﹣2=5,
设点P(x,0),
则PB′2=22+x2=52,解得x,
故点P的坐标为(,0)或(,0).
15.【解答】解:(1)∵|a﹣3|=0,
∴,
解得:a=b=3;
(2)当P点运动时,PE的值不变化,PE=3,理由为:
过O作OC⊥AB,
∵OA=OB=3,C为斜边AB的中点,
∴AB6,即OCAB=3,
∵△AOB为等腰直角三角形,
∴AC=BC,∠AOC=∠BOC=45°,
∵PO=PD,
∴∠POD=∠PDO,
∵∠POD=45°+∠POC,∠PDO=45°+∠APD,
∴∠POC=∠APD,
在△POC和△DPE中,
,
∴△POC≌△DPE(AAS),
∴OC=PE=3;
(3)∵OP=DP,∠OPD=45°,
∴∠POD=∠PDO67.5°,
∴∠PDA=180°﹣∠PDO=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°﹣45°=22.5°,
∴∠BPO=180°﹣∠OPD﹣∠APD=112.5°,
∴∠PDA=∠BPO,
在△POB和△DPA中,
,
∴△POB≌△DPA(AAS),
∴OB=PA=OA=3,
∴DA=PB=6﹣3,
∴OD=OA﹣DA=3(6﹣3)=66,
则D(66,0).
21世纪教育网(www.21cnjy.com)
同课章节目录
