2024-2025学年八年级下学期数学期中测试(广东省广州市专用)(含答案)
文档属性
| 名称 | 2024-2025学年八年级下学期数学期中测试(广东省广州市专用)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 310.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 10:14:13 | ||
图片预览



文档简介
保密★启用前
2024-2025学年八级下册期中考试(广州市专用)
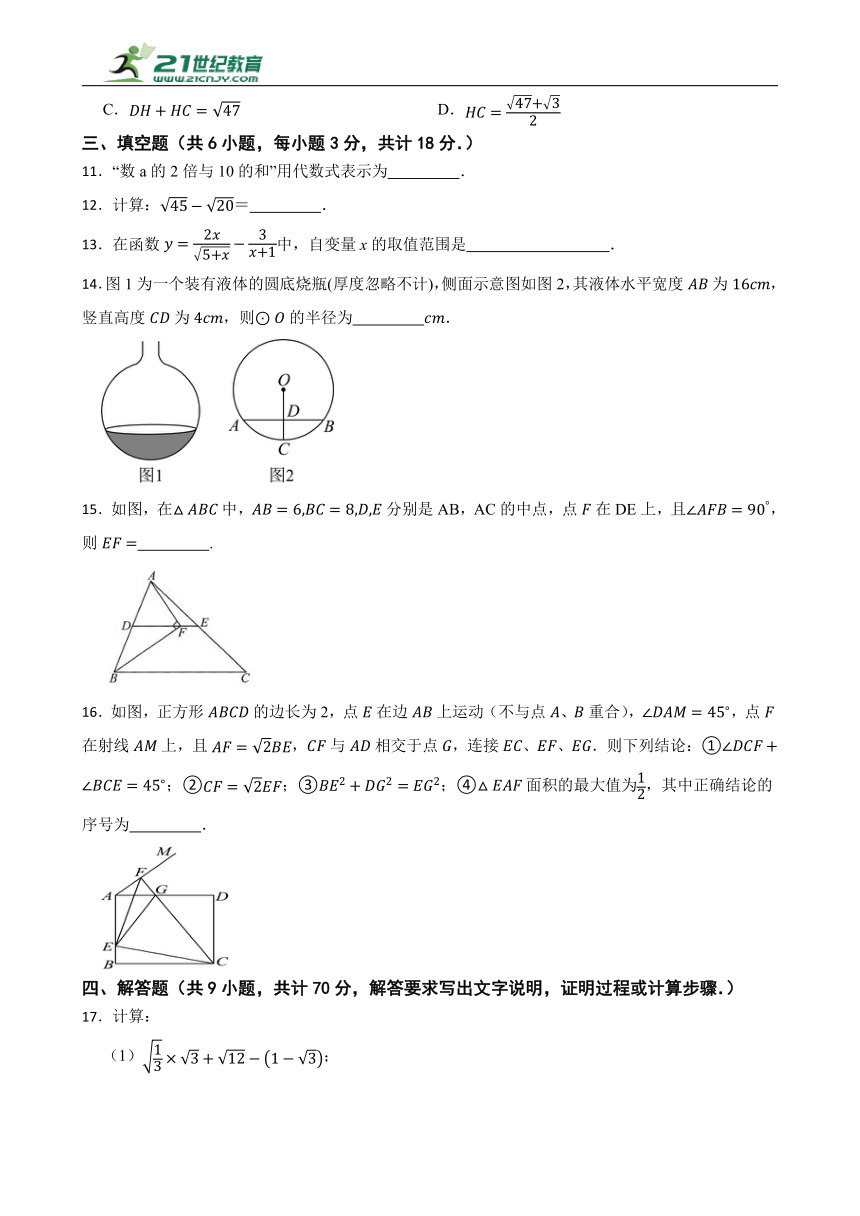
数学
考试范围:人教版八下第十六章-第十七章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(共8小题,每小题3分,每小题只有一个选项符合题目要求,共计24分.)
1.下列各式中,能与合并的是( )
A. B.4 C. D.
2.在进行路程s,速度v,时间t的相关计算中,若路程s不变,则下列说法不正确的是( )
A.速度v是变量 B.速度v,时间t都是变量
C.时间t是变量 D.路程s,速度v,时间t都是常量
3.如图,在正方形网格中,的顶点都在格点上,则( )
A. B. C. D.
4.下列命题中正确的是( )
A.正方形的面积等于对角线平方的一半
B.邻边相等的平行四边形是正方形
C.对角线互相垂直的四边形是菱形
D.矩形的对角线相等且互相垂直
5.下列选项中,计算正确的是( )
A. B. C. D.
6.的三边长分别为,,,由下列条件不能判断为直角三角形的是( )
A. B.
C.,, D.
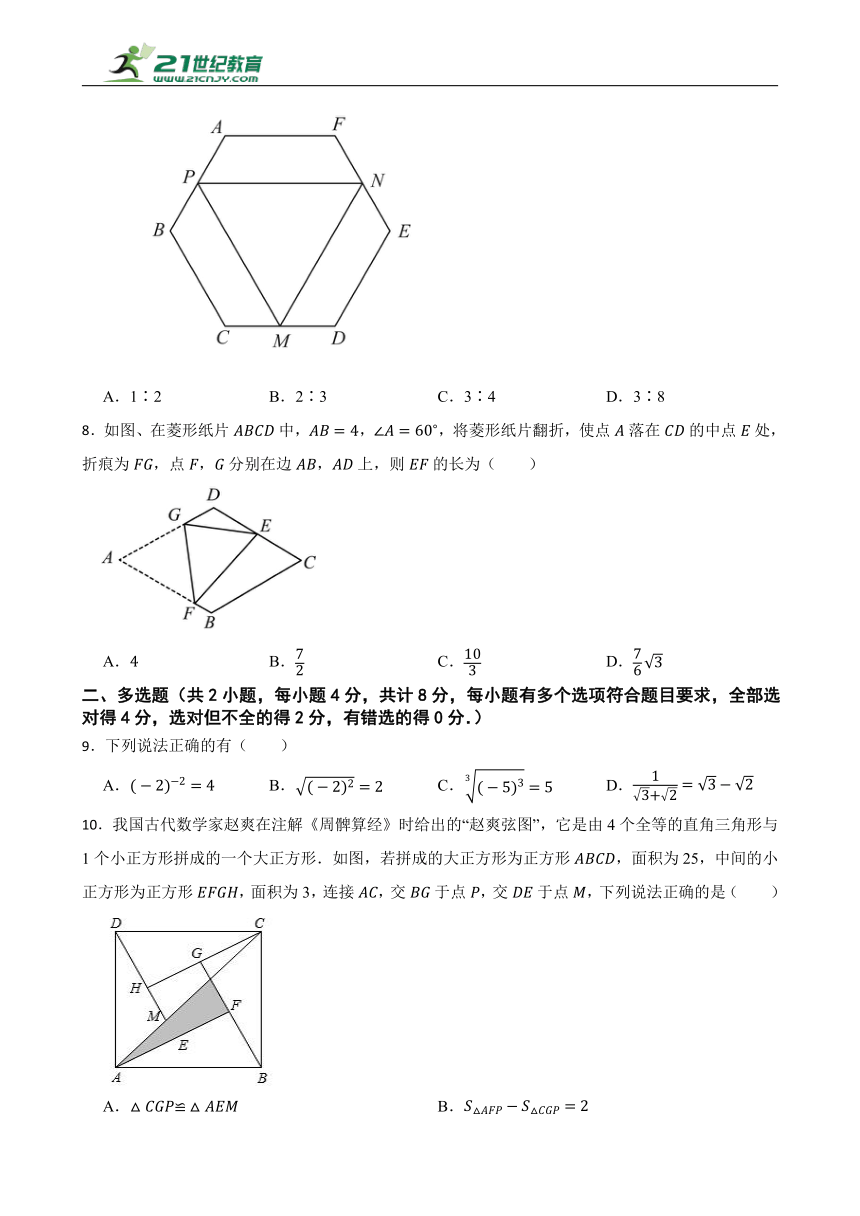
7.如图,正三角形PMN的顶点分别是正六边形ABCDEF三边的中点,则正三角形 PMN与正六边形ABCDEF的周长之比( )
A.1∶2 B.2∶3 C.3∶4 D.3∶8
8.如图、在菱形纸片中,,,将菱形纸片翻折,使点落在的中点处,折痕为,点,分别在边,上,则的长为( )
A. B. C. D.
二、多选题(共2小题,每小题4分,共计8分,每小题有多个选项符合题目要求,全部选对得4分,选对但不全的得2分,有错选的得0分.)
9.下列说法正确的有( )
A. B. C. D.
10.我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形.如图,若拼成的大正方形为正方形,面积为25,中间的小正方形为正方形,面积为3,连接,交于点,交于点,下列说法正确的是( )
A. B.
C. D.
三、填空题(共6小题,每小题3分,共计18分.)
11.“数a的2倍与10的和”用代数式表示为 .
12.计算:= .
13.在函数中,自变量x的取值范围是 .
14.图1为一个装有液体的圆底烧瓶(厚度忽略不计),侧面示意图如图2,其液体水平宽度为,竖直高度为,则的半径为 .
15.如图,在中,分别是AB,AC的中点,点在DE上,且,则 .
16.如图,正方形的边长为2,点在边上运动(不与点、重合),,点在射线上,且,与相交于点,连接、、.则下列结论:①;②;③;④面积的最大值为,其中正确结论的序号为 .
四、解答题(共9小题,共计70分,解答要求写出文字说明,证明过程或计算步骤.)
17.计算:
(1);
(2)解方程组:
18.如图,在平行四边形中,点、分别在、延长线上,且求证:四边形为平行四边形.
19.已知,,分别求下列代数式的值:
(1);
(2).
20.如图,在的网格中,每个小正方形的边长均为1,连接小正方形的三个顶点得到,小正方形的顶点D在的边AB上,解答下列问题:
(1)判断的形状并求出其周长;
(2)求和的周长之差.
21.如图,在中.,是的中线,如果..求的值.
22.如图,在中,,,,垂直平分,分别交边、于点、,连结.
(1)求的度数;
(2)求的长.
23.已知,.
(1)求的值;
(2)求的值.
24.如图,在中,,过点的直线,为上一点,过点作,交直线于点,垂足为,连接,.
(1)求证:;
(2)当点是的中点时,四边形是什么特殊四边形?请说明你的理由;
(3)请直接写出在的条件下,当 时,四边形是正方形.
25.“做数学”可以帮助我们积累数学活动经验.
【初步感知】数学课上,同学们用纸片进行折纸操作.
如图①,在中,,,.将沿着翻折,使点A落在AB边上的处,且,则______,______.
【方法探索】折纸,常常能为证明一个命题提供思路和方法.
小明遇到这样一个问题:如图②,在中,,,平分,求证:.小明的思路如下:如图③,将沿翻折,使点落在边上的处,连接,
(1)请完成小明的证明过程;
(2)如图④,是边上的高线,其他条件不变,请你用刚刚获得的方法探索、、之间的数量关系,并直接写出它们之间的数量关系______.
【思维拓展】
如图⑤,在中,,,,、是边上的点,连接、,先将边沿折叠,使点的对称点落在边上:再将边沿折叠,使点的对称点落在的延长线上,则线段的长为______.
答案解析部分
1.D
2.D
解:在进行路程S、速度v和时间t的相关计算中,若保持行驶路程不变,则v、t是变量,S是常量.
故答案为D.
本题考查常量与变量.变量的定义:一个变化的过程中,数值发生变化的量叫变量;常量的定义:数值始终不变的量称为常量.利用常量和变量定义可选出选项.
3.B
4.A
5.B
6.B
7.C
8.B
9.B,D
10.A,C,D
11.2a+10
数a的2倍为2a,加10为:2a+10.
先求倍数,然后求和.
12.
13.且
解:由题意得:
∴且,
故答案为:且.
根据二次根式有意义的条件:被开方数大于等于0,然后根据分式有意义的条件:分母不为0,据此得到:,解此式子即可求解.
14.10
15.1
解:∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=4,
∵∠AFB=90°,D是AB的中点,
∴DF=AB=3,
∴EF=DE DF=4 3=1,
故答案为:1.
先利用三角形中位线的性质可得DE=BC=4,再利用直角三角形斜边上中线的性质可得DF=AB=3,最后利用线段的和差求出EF的长即可.
16.①②④
17.(1)
(2)
18.证明:四边形为平行四边形,
,,
,,
,
,
,,
四边形为平行四边形.
利用平行四边形的性质,证得ED=BF,再根据ED∥BF,即可证得四边形EBFD为平行四边形.
19.(1)解:∵,,
∴
,
;
(2)解:∵,
∴,
.
本题考查二次根式的化简求值;熟练运用平方差公式是解题关键.
平方差公式:
(1)根据a和b的值先求出a+b与a-b的值,即a+b=6,,再根据平方差公式,代入数据计算即可得出答案;
(2)根据a和b的值先求出ab与a-b的值,即:ab=1,,再将分式通分得:,代入数据计算即可得出答案.
20.(1)解:,
是等腰三角形,
;
(2)解:,
;
,
.即与的周长之差为
(1)利用勾股定理分别求出△ABC三边的长度,易得△ABC是等腰三角形,继而求出周长。
(2)根据图形可以得出△ACD与△BCD 周长只差为AD-BD,利用勾股定理以此求出AD、BD的长即可解决问题。
21.
22.(1)
(2)
23.(1)1
(2)
24.(1)证明:,
,
,
,
,
,即,
四边形是平行四边形,
;
(2)解:四边形是菱形,
理由是:为中点,
,
,
,
,
四边形是平行四边形,
,为中点,
,
四边形是菱形;
(3)45
解:(3)若为中点,当∠A=45°时,四边形BECD是正方形,
理由:∵∠A=45°,∠ACB=90°,
∴∠ABC=45°,
∵四边形BECD是菱形,
∴CD=DB,
∴∠DBC=∠DCB=45°,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴四边形BECD是正方形;
故答案为:45°.
(1)由垂直的定义可得=90°,可得AC∥DE,由CE∥AD,根据两组对边分别平行可证四边形是平行四边形,利用平行四边形的性质即得结论;
(2) 四边形是菱形,理由:先证四边形是平行四边形, 由直角三角形斜边中线的性质可得CD=BD,根据菱形的判定即证结论;
(3)当∠A=45°时,四边形BECD是正方形,根据正方形的判定定理证明即可.
25.[初步感知],;
[方法探索](1)见证明:(2).
[思维拓展].
2024-2025学年八级下册期中考试(广州市专用)
数学
考试范围:人教版八下第十六章-第十七章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(共8小题,每小题3分,每小题只有一个选项符合题目要求,共计24分.)
1.下列各式中,能与合并的是( )
A. B.4 C. D.
2.在进行路程s,速度v,时间t的相关计算中,若路程s不变,则下列说法不正确的是( )
A.速度v是变量 B.速度v,时间t都是变量
C.时间t是变量 D.路程s,速度v,时间t都是常量
3.如图,在正方形网格中,的顶点都在格点上,则( )
A. B. C. D.
4.下列命题中正确的是( )
A.正方形的面积等于对角线平方的一半
B.邻边相等的平行四边形是正方形
C.对角线互相垂直的四边形是菱形
D.矩形的对角线相等且互相垂直
5.下列选项中,计算正确的是( )
A. B. C. D.
6.的三边长分别为,,,由下列条件不能判断为直角三角形的是( )
A. B.
C.,, D.
7.如图,正三角形PMN的顶点分别是正六边形ABCDEF三边的中点,则正三角形 PMN与正六边形ABCDEF的周长之比( )
A.1∶2 B.2∶3 C.3∶4 D.3∶8
8.如图、在菱形纸片中,,,将菱形纸片翻折,使点落在的中点处,折痕为,点,分别在边,上,则的长为( )
A. B. C. D.
二、多选题(共2小题,每小题4分,共计8分,每小题有多个选项符合题目要求,全部选对得4分,选对但不全的得2分,有错选的得0分.)
9.下列说法正确的有( )
A. B. C. D.
10.我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形.如图,若拼成的大正方形为正方形,面积为25,中间的小正方形为正方形,面积为3,连接,交于点,交于点,下列说法正确的是( )
A. B.
C. D.
三、填空题(共6小题,每小题3分,共计18分.)
11.“数a的2倍与10的和”用代数式表示为 .
12.计算:= .
13.在函数中,自变量x的取值范围是 .
14.图1为一个装有液体的圆底烧瓶(厚度忽略不计),侧面示意图如图2,其液体水平宽度为,竖直高度为,则的半径为 .
15.如图,在中,分别是AB,AC的中点,点在DE上,且,则 .
16.如图,正方形的边长为2,点在边上运动(不与点、重合),,点在射线上,且,与相交于点,连接、、.则下列结论:①;②;③;④面积的最大值为,其中正确结论的序号为 .
四、解答题(共9小题,共计70分,解答要求写出文字说明,证明过程或计算步骤.)
17.计算:
(1);
(2)解方程组:
18.如图,在平行四边形中,点、分别在、延长线上,且求证:四边形为平行四边形.
19.已知,,分别求下列代数式的值:
(1);
(2).
20.如图,在的网格中,每个小正方形的边长均为1,连接小正方形的三个顶点得到,小正方形的顶点D在的边AB上,解答下列问题:
(1)判断的形状并求出其周长;
(2)求和的周长之差.
21.如图,在中.,是的中线,如果..求的值.
22.如图,在中,,,,垂直平分,分别交边、于点、,连结.
(1)求的度数;
(2)求的长.
23.已知,.
(1)求的值;
(2)求的值.
24.如图,在中,,过点的直线,为上一点,过点作,交直线于点,垂足为,连接,.
(1)求证:;
(2)当点是的中点时,四边形是什么特殊四边形?请说明你的理由;
(3)请直接写出在的条件下,当 时,四边形是正方形.
25.“做数学”可以帮助我们积累数学活动经验.
【初步感知】数学课上,同学们用纸片进行折纸操作.
如图①,在中,,,.将沿着翻折,使点A落在AB边上的处,且,则______,______.
【方法探索】折纸,常常能为证明一个命题提供思路和方法.
小明遇到这样一个问题:如图②,在中,,,平分,求证:.小明的思路如下:如图③,将沿翻折,使点落在边上的处,连接,
(1)请完成小明的证明过程;
(2)如图④,是边上的高线,其他条件不变,请你用刚刚获得的方法探索、、之间的数量关系,并直接写出它们之间的数量关系______.
【思维拓展】
如图⑤,在中,,,,、是边上的点,连接、,先将边沿折叠,使点的对称点落在边上:再将边沿折叠,使点的对称点落在的延长线上,则线段的长为______.
答案解析部分
1.D
2.D
解:在进行路程S、速度v和时间t的相关计算中,若保持行驶路程不变,则v、t是变量,S是常量.
故答案为D.
本题考查常量与变量.变量的定义:一个变化的过程中,数值发生变化的量叫变量;常量的定义:数值始终不变的量称为常量.利用常量和变量定义可选出选项.
3.B
4.A
5.B
6.B
7.C
8.B
9.B,D
10.A,C,D
11.2a+10
数a的2倍为2a,加10为:2a+10.
先求倍数,然后求和.
12.
13.且
解:由题意得:
∴且,
故答案为:且.
根据二次根式有意义的条件:被开方数大于等于0,然后根据分式有意义的条件:分母不为0,据此得到:,解此式子即可求解.
14.10
15.1
解:∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=4,
∵∠AFB=90°,D是AB的中点,
∴DF=AB=3,
∴EF=DE DF=4 3=1,
故答案为:1.
先利用三角形中位线的性质可得DE=BC=4,再利用直角三角形斜边上中线的性质可得DF=AB=3,最后利用线段的和差求出EF的长即可.
16.①②④
17.(1)
(2)
18.证明:四边形为平行四边形,
,,
,,
,
,
,,
四边形为平行四边形.
利用平行四边形的性质,证得ED=BF,再根据ED∥BF,即可证得四边形EBFD为平行四边形.
19.(1)解:∵,,
∴
,
;
(2)解:∵,
∴,
.
本题考查二次根式的化简求值;熟练运用平方差公式是解题关键.
平方差公式:
(1)根据a和b的值先求出a+b与a-b的值,即a+b=6,,再根据平方差公式,代入数据计算即可得出答案;
(2)根据a和b的值先求出ab与a-b的值,即:ab=1,,再将分式通分得:,代入数据计算即可得出答案.
20.(1)解:,
是等腰三角形,
;
(2)解:,
;
,
.即与的周长之差为
(1)利用勾股定理分别求出△ABC三边的长度,易得△ABC是等腰三角形,继而求出周长。
(2)根据图形可以得出△ACD与△BCD 周长只差为AD-BD,利用勾股定理以此求出AD、BD的长即可解决问题。
21.
22.(1)
(2)
23.(1)1
(2)
24.(1)证明:,
,
,
,
,
,即,
四边形是平行四边形,
;
(2)解:四边形是菱形,
理由是:为中点,
,
,
,
,
四边形是平行四边形,
,为中点,
,
四边形是菱形;
(3)45
解:(3)若为中点,当∠A=45°时,四边形BECD是正方形,
理由:∵∠A=45°,∠ACB=90°,
∴∠ABC=45°,
∵四边形BECD是菱形,
∴CD=DB,
∴∠DBC=∠DCB=45°,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴四边形BECD是正方形;
故答案为:45°.
(1)由垂直的定义可得=90°,可得AC∥DE,由CE∥AD,根据两组对边分别平行可证四边形是平行四边形,利用平行四边形的性质即得结论;
(2) 四边形是菱形,理由:先证四边形是平行四边形, 由直角三角形斜边中线的性质可得CD=BD,根据菱形的判定即证结论;
(3)当∠A=45°时,四边形BECD是正方形,根据正方形的判定定理证明即可.
25.[初步感知],;
[方法探索](1)见证明:(2).
[思维拓展].
同课章节目录
