2024-2025学年七年级下学期数学期中测试(浙江杭州市专用)(含答案)
文档属性
| 名称 | 2024-2025学年七年级下学期数学期中测试(浙江杭州市专用)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 244.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览

文档简介
保密★启用前
2024-2025学年七年级下册期中考试(杭州市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列运动属于平移的是( )
A.空中放飞的风筝
B.乒乓球比赛中的高抛发球后,乒乓球的运动方式
C.篮球被运动员投出并进入篮筐的过程
D.茅台机场的飞机降落时在笔直的跑道上滑行
2.科技日新月异,我国科学家研发出无需“插电”的发光发电纤维,其直径可在0.0002米至0.0005米之间精确调控,0.0005米用科学记数法可表示为( )
A.米 B.米 C.米 D.米
3.下列命题正确的是( )
A.三角形的三条高交于一点
B.过一点有且只有一条直线与已知直线平行
C.两条直线被第三条直线所截,内错角相等
D.底角和腰分别相等的两个等腰三角形全等
4.下列算式中,是二元一次方程的是( )
A. B.
C. D.
5.用加减数解方程组时,若要消去y,则应( )
A.①② B.①②
C.①② D.① - ②
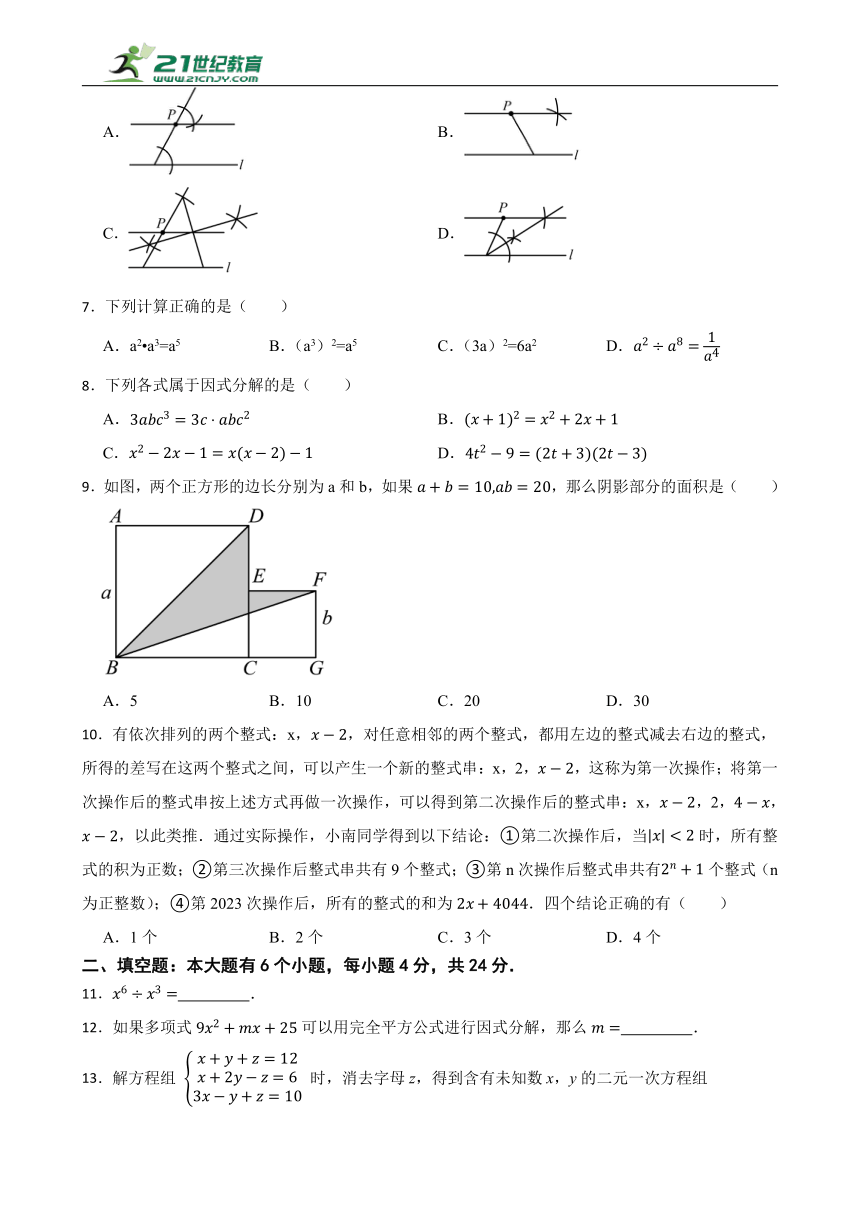
6.数学活动课上,四位同学围绕作图问题“已知直线l和直线l外一点P,用无刻度的直尺和圆规过点P作l的平行线”分别作出了下列图形,其中作法不正确的是( )
A. B.
C. D.
7.下列计算正确的是( )
A.a2 a3=a5 B.(a3)2=a5 C.(3a)2=6a2 D.
8.下列各式属于因式分解的是( )
A. B.
C. D.
9.如图,两个正方形的边长分别为a和b,如果,那么阴影部分的面积是( )
A.5 B.10 C.20 D.30
10.有依次排列的两个整式:x,,对任意相邻的两个整式,都用左边的整式减去右边的整式,所得的差写在这两个整式之间,可以产生一个新的整式串:x,2,,这称为第一次操作;将第一次操作后的整式串按上述方式再做一次操作,可以得到第二次操作后的整式串:x,,2,,,以此类推.通过实际操作,小南同学得到以下结论:①第二次操作后,当时,所有整式的积为正数;②第三次操作后整式串共有9个整式;③第n次操作后整式串共有个整式(n为正整数);④第2023次操作后,所有的整式的和为.四个结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题有6个小题,每小题4分,共24分.
11. .
12.如果多项式可以用完全平方公式进行因式分解,那么 .
13.解方程组 时,消去字母z,得到含有未知数x,y的二元一次方程组是 .
14.已知是方程组的解,则的值是 .
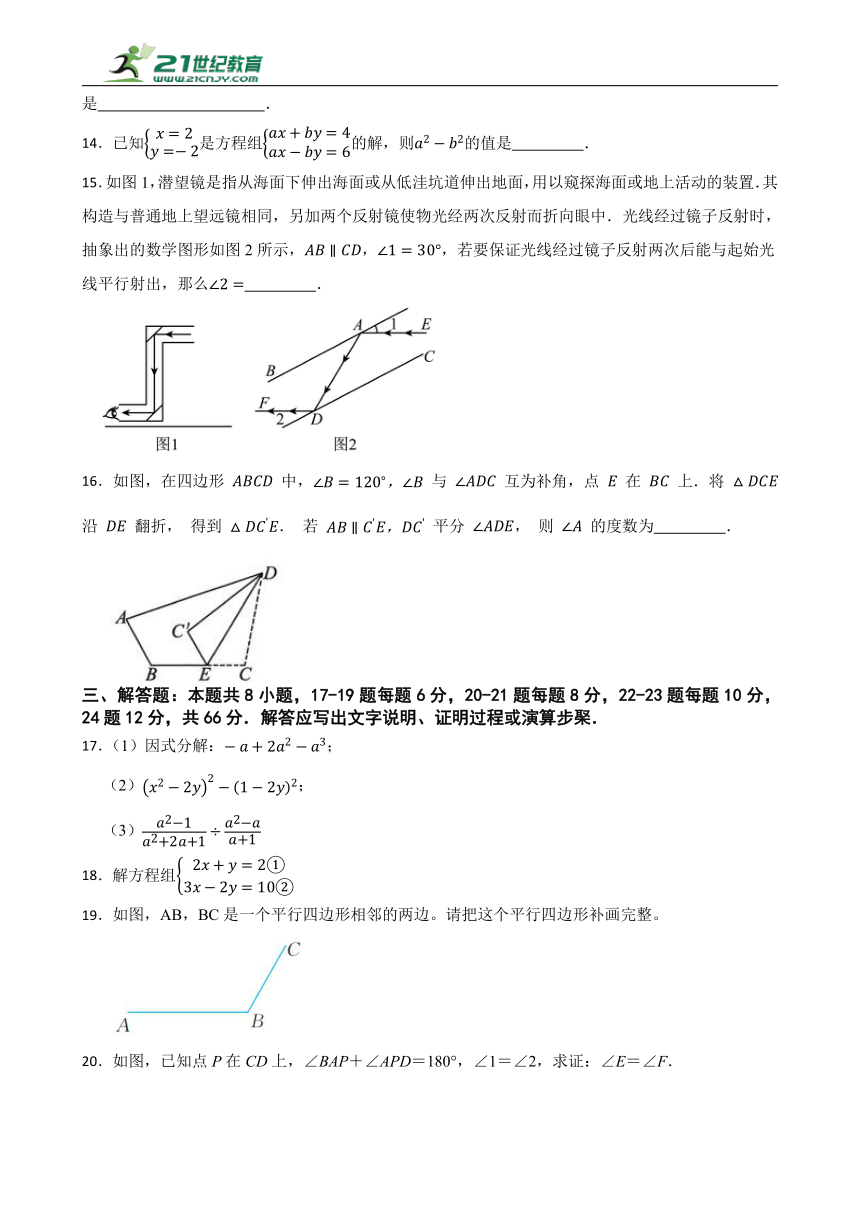
15.如图1,潜望镜是指从海面下伸出海面或从低洼坑道伸出地面,用以窥探海面或地上活动的装置.其构造与普通地上望远镜相同,另加两个反射镜使物光经两次反射而折向眼中.光线经过镜子反射时,抽象出的数学图形如图2所示,,,若要保证光线经过镜子反射两次后能与起始光线平行射出,那么 .
16. 如图, 在四边形 中, 与 互为补角, 点 在 上. 将 沿 翻折, 得到 . 若 平分 , 则 的度数为 .
三、解答题:本题共8小题,17-19题每题6分,20-21题每题8分,22-23题每题10分,24题12分,共66分.解答应写出文字说明、证明过程或演算步棸.
17.(1)因式分解:;
(2);
(3)
18.解方程组
19.如图,AB,BC是一个平行四边形相邻的两边。请把这个平行四边形补画完整。
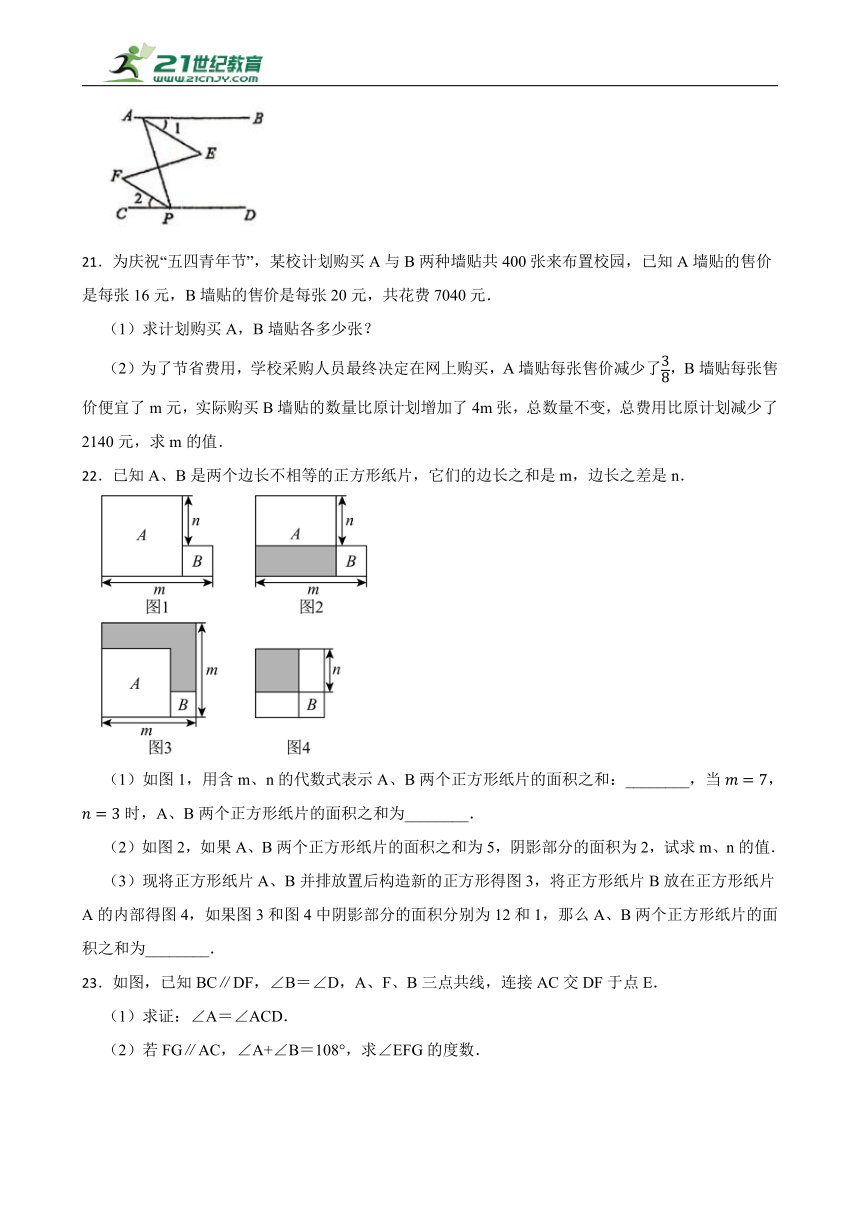
20.如图,已知点P在CD上,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.
21.为庆祝“五四青年节”,某校计划购买A与B两种墙贴共400张来布置校园,已知A墙贴的售价是每张16元,B墙贴的售价是每张20元,共花费7040元.
(1)求计划购买A,B墙贴各多少张?
(2)为了节省费用,学校采购人员最终决定在网上购买,A墙贴每张售价减少了,B墙贴每张售价便宜了m元,实际购买B墙贴的数量比原计划增加了4m张,总数量不变,总费用比原计划减少了2140元,求m的值.
22.已知A、B是两个边长不相等的正方形纸片,它们的边长之和是m,边长之差是n.
(1)如图1,用含m、n的代数式表示A、B两个正方形纸片的面积之和:________,当,时,A、B两个正方形纸片的面积之和为________.
(2)如图2,如果A、B两个正方形纸片的面积之和为5,阴影部分的面积为2,试求m、n的值.
(3)现将正方形纸片A、B并排放置后构造新的正方形得图3,将正方形纸片B放在正方形纸片A的内部得图4,如果图3和图4中阴影部分的面积分别为12和1,那么A、B两个正方形纸片的面积之和为________.
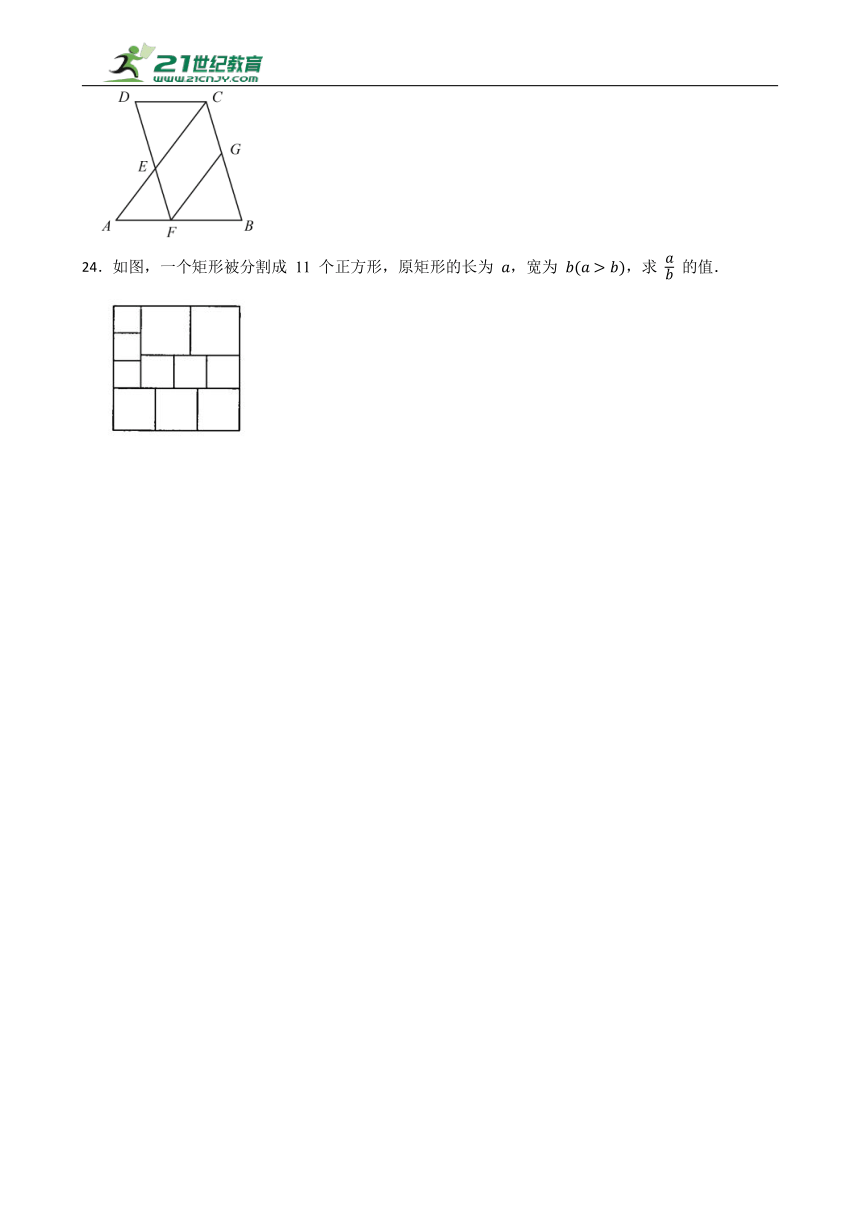
23.如图,已知BC∥DF,∠B=∠D,A、F、B三点共线,连接AC交DF于点E.
(1)求证:∠A=∠ACD.
(2)若FG∥AC,∠A+∠B=108°,求∠EFG的度数.
24.如图,一个矩形被分割成 11 个正方形,原矩形的长为 ,宽为 ,求 的值.
答案解析部分
1.D
2.A
解:,
故选:A.
根据科学记数法的形式进行表示即可,即一般形式为,其中.,n为由原数左边起第一个不为零的数字前面的0的个数所决定是解题的关键.与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
3.D
解:A中,由三角形的三条高所在直线交于一点,所以A不符合题意;
B中,由过直线外一点有且只有一条直线与已知直线平行,所以B不符合题意;
C中,由两条平行直线被第三条直线所截,内错角相等,所以 C不符合题意;
D中,由底角和腰分别相等的两个等腰三角形全等,正确,所以D符合题意,
故选:D.
本题考查了平行公理,三角形的高,平行线性质,全等三角形的判定,根据平行公理,三角形的高,平行线性质,全等三角形的判定定理,结合选项,逐项分析判断,即可得到答案.
4.A
5.C
解:∵3y×5+(-5y)×3=0,
∴用加减数解方程组时,若要消去y,则应 ①②.
故答案为:C.
由于方程组中未知数y的系数符号相反,且两个系数绝对值的最小公倍数为15,故要消去y,只需要①×5+②×3即可.
6.B
解:A.根据作图可知,,
∴,故A正确,不符合题意;
B.根据作图无法判断所作直线与l平行,故B错误,符合题意;
C.根据作图可知,P为的中点,为的中点,
∴,故C正确,不符合题意;
D.根据作图可知,平分,,
则,,
∴,
∴,故D正确,不符合题意.
故答案为:B.
根据主线平行判定定理逐项进行判断即可求出答案.
7.A
A、∵a2 a3=a5,故原题计算正确;
B、∵(a3)2=a6,故原题计算错误;
C、∵(3a)2=9a2,故原题计算错误;
D、∵a2÷a8= a-6= 故原题计算错误;
故答案为:A.
A根据同底数幂的乘法计算;B根据幂的乘方计算;C根据积的乘方法则计算;D根据同底数幂的除法法则计算.
8.D
9.C
10.C
11.
解:.
故答案为:.
本题主要考查了同底数幂的除法的运算法则,同底数幂的除法运算法则是:同底数幂相除,底数不变,指数相减,据此运算,即可得到答案.
12.
13.
解: ,
①+②得出2x+3y=18④,
②+③得出4x+y=16⑤,
由④和⑤组成方程组 ,
故答案为: .
根据题意先得出①+③后的方程,再得到① 2-②的方程,从而得出二元一次方程组。
14.6
解:∵是方程组的解,
∴即,
∴==2×3=6,
故答案为:6.
将方程组的解代入方程组中,得到关于a,b的方程组,再利用平方差公式(=)代入计算.
15.
解:由光的反射定律得:,,
∵,
,
,
,,
,
.
故答案为:.
根据由光的反射定律“入射角等于反射角”可得,,由平行线的性质“两直线平行,内错角相等”可得,再根据内错角相等两直线平行即可求解.
16.80°
17.(1)
(2)
(3)
18.解:①×2得:4x+2y=4 ③②+③得:7x=14
∴x=2
把x=2代入①得:y= 2
∴原方程组的解为:
本题主要考查了二元一次方程的解法,利用加减消元法:二元一次方程组的两个方程中同一未知数的系数互为相反数或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,进而求得方程组的解,即可得到答案.
19.解:如图所示,过点作,且CF与AE相交于点,则四边形ABCD即为所求作的平行四边形。
过点作,且CF与AE相交于点,进而根据平行四边形的判定定理即可求解.
20.证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥CD.(同旁内角互补,两直线平行)
∴∠BAP=∠CPA.(两直线平行,内错角相等)
∵∠1=∠2,(已知)
∴∠BAP-∠1=∠CPA-∠2
∴∠EAP=∠FPA.
∴AE∥PF.(内错角相等,两直线平行)
∴∠E=∠F.(两直线平行,内错角相等)
利用同旁内角互补,两直线平行可证得AB∥CD,利用平行线的性质可推出∠BAP=∠CPA,结合已知条件可证得∠EAP=∠FPA;再利用内错角相等,两直线平行可证得AE∥PF,然后利用平行线的性质可证得结论.
21.(1)购买240张墙贴,购买160张墙贴
(2)5
22.(1),;
(2),;
(3)
23.(1)证明:∵BC∥DF,
∴∠B+∠BFD=180°,
∵∠B=∠D,
∴∠D+∠BFD=180°,
∴AB∥CD,
∴∠A=∠ACD;
(2)解:∵∠A+∠B=108°,
∴∠ACB=72°,
∵FG∥AC,
∴∠BGF=72°,
∵BC∥DF,
∴∠EFG=72°.
(1)根据两直线平行,同旁内角互补得到∠B+∠BFD=180°,根据等量关系得到∠D+∠BFD=180°,即可得到AB∥CD证明结论;(2)利用三角形内角和定理求出∠ACB的度数,然后根据两直线平行,同位角相等求出∠BGF的度数,再根据两直线平行,内错角相等解题即可.
24.解:设矩形中较小的正方形的边长为x,较大的正方形的边长为y,
根据题意得 ,
解得,
∵b=3x+=,
∴.
设矩形中较小的正方形的边长为x,较大的正方形的边长为y,根据图形中边长之间的关系可得,求出x、y的值,再求出b=3x+=,最后求出即可.
2024-2025学年七年级下册期中考试(杭州市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列运动属于平移的是( )
A.空中放飞的风筝
B.乒乓球比赛中的高抛发球后,乒乓球的运动方式
C.篮球被运动员投出并进入篮筐的过程
D.茅台机场的飞机降落时在笔直的跑道上滑行
2.科技日新月异,我国科学家研发出无需“插电”的发光发电纤维,其直径可在0.0002米至0.0005米之间精确调控,0.0005米用科学记数法可表示为( )
A.米 B.米 C.米 D.米
3.下列命题正确的是( )
A.三角形的三条高交于一点
B.过一点有且只有一条直线与已知直线平行
C.两条直线被第三条直线所截,内错角相等
D.底角和腰分别相等的两个等腰三角形全等
4.下列算式中,是二元一次方程的是( )
A. B.
C. D.
5.用加减数解方程组时,若要消去y,则应( )
A.①② B.①②
C.①② D.① - ②
6.数学活动课上,四位同学围绕作图问题“已知直线l和直线l外一点P,用无刻度的直尺和圆规过点P作l的平行线”分别作出了下列图形,其中作法不正确的是( )
A. B.
C. D.
7.下列计算正确的是( )
A.a2 a3=a5 B.(a3)2=a5 C.(3a)2=6a2 D.
8.下列各式属于因式分解的是( )
A. B.
C. D.
9.如图,两个正方形的边长分别为a和b,如果,那么阴影部分的面积是( )
A.5 B.10 C.20 D.30
10.有依次排列的两个整式:x,,对任意相邻的两个整式,都用左边的整式减去右边的整式,所得的差写在这两个整式之间,可以产生一个新的整式串:x,2,,这称为第一次操作;将第一次操作后的整式串按上述方式再做一次操作,可以得到第二次操作后的整式串:x,,2,,,以此类推.通过实际操作,小南同学得到以下结论:①第二次操作后,当时,所有整式的积为正数;②第三次操作后整式串共有9个整式;③第n次操作后整式串共有个整式(n为正整数);④第2023次操作后,所有的整式的和为.四个结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题有6个小题,每小题4分,共24分.
11. .
12.如果多项式可以用完全平方公式进行因式分解,那么 .
13.解方程组 时,消去字母z,得到含有未知数x,y的二元一次方程组是 .
14.已知是方程组的解,则的值是 .
15.如图1,潜望镜是指从海面下伸出海面或从低洼坑道伸出地面,用以窥探海面或地上活动的装置.其构造与普通地上望远镜相同,另加两个反射镜使物光经两次反射而折向眼中.光线经过镜子反射时,抽象出的数学图形如图2所示,,,若要保证光线经过镜子反射两次后能与起始光线平行射出,那么 .
16. 如图, 在四边形 中, 与 互为补角, 点 在 上. 将 沿 翻折, 得到 . 若 平分 , 则 的度数为 .
三、解答题:本题共8小题,17-19题每题6分,20-21题每题8分,22-23题每题10分,24题12分,共66分.解答应写出文字说明、证明过程或演算步棸.
17.(1)因式分解:;
(2);
(3)
18.解方程组
19.如图,AB,BC是一个平行四边形相邻的两边。请把这个平行四边形补画完整。
20.如图,已知点P在CD上,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.
21.为庆祝“五四青年节”,某校计划购买A与B两种墙贴共400张来布置校园,已知A墙贴的售价是每张16元,B墙贴的售价是每张20元,共花费7040元.
(1)求计划购买A,B墙贴各多少张?
(2)为了节省费用,学校采购人员最终决定在网上购买,A墙贴每张售价减少了,B墙贴每张售价便宜了m元,实际购买B墙贴的数量比原计划增加了4m张,总数量不变,总费用比原计划减少了2140元,求m的值.
22.已知A、B是两个边长不相等的正方形纸片,它们的边长之和是m,边长之差是n.
(1)如图1,用含m、n的代数式表示A、B两个正方形纸片的面积之和:________,当,时,A、B两个正方形纸片的面积之和为________.
(2)如图2,如果A、B两个正方形纸片的面积之和为5,阴影部分的面积为2,试求m、n的值.
(3)现将正方形纸片A、B并排放置后构造新的正方形得图3,将正方形纸片B放在正方形纸片A的内部得图4,如果图3和图4中阴影部分的面积分别为12和1,那么A、B两个正方形纸片的面积之和为________.
23.如图,已知BC∥DF,∠B=∠D,A、F、B三点共线,连接AC交DF于点E.
(1)求证:∠A=∠ACD.
(2)若FG∥AC,∠A+∠B=108°,求∠EFG的度数.
24.如图,一个矩形被分割成 11 个正方形,原矩形的长为 ,宽为 ,求 的值.
答案解析部分
1.D
2.A
解:,
故选:A.
根据科学记数法的形式进行表示即可,即一般形式为,其中.,n为由原数左边起第一个不为零的数字前面的0的个数所决定是解题的关键.与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
3.D
解:A中,由三角形的三条高所在直线交于一点,所以A不符合题意;
B中,由过直线外一点有且只有一条直线与已知直线平行,所以B不符合题意;
C中,由两条平行直线被第三条直线所截,内错角相等,所以 C不符合题意;
D中,由底角和腰分别相等的两个等腰三角形全等,正确,所以D符合题意,
故选:D.
本题考查了平行公理,三角形的高,平行线性质,全等三角形的判定,根据平行公理,三角形的高,平行线性质,全等三角形的判定定理,结合选项,逐项分析判断,即可得到答案.
4.A
5.C
解:∵3y×5+(-5y)×3=0,
∴用加减数解方程组时,若要消去y,则应 ①②.
故答案为:C.
由于方程组中未知数y的系数符号相反,且两个系数绝对值的最小公倍数为15,故要消去y,只需要①×5+②×3即可.
6.B
解:A.根据作图可知,,
∴,故A正确,不符合题意;
B.根据作图无法判断所作直线与l平行,故B错误,符合题意;
C.根据作图可知,P为的中点,为的中点,
∴,故C正确,不符合题意;
D.根据作图可知,平分,,
则,,
∴,
∴,故D正确,不符合题意.
故答案为:B.
根据主线平行判定定理逐项进行判断即可求出答案.
7.A
A、∵a2 a3=a5,故原题计算正确;
B、∵(a3)2=a6,故原题计算错误;
C、∵(3a)2=9a2,故原题计算错误;
D、∵a2÷a8= a-6= 故原题计算错误;
故答案为:A.
A根据同底数幂的乘法计算;B根据幂的乘方计算;C根据积的乘方法则计算;D根据同底数幂的除法法则计算.
8.D
9.C
10.C
11.
解:.
故答案为:.
本题主要考查了同底数幂的除法的运算法则,同底数幂的除法运算法则是:同底数幂相除,底数不变,指数相减,据此运算,即可得到答案.
12.
13.
解: ,
①+②得出2x+3y=18④,
②+③得出4x+y=16⑤,
由④和⑤组成方程组 ,
故答案为: .
根据题意先得出①+③后的方程,再得到① 2-②的方程,从而得出二元一次方程组。
14.6
解:∵是方程组的解,
∴即,
∴==2×3=6,
故答案为:6.
将方程组的解代入方程组中,得到关于a,b的方程组,再利用平方差公式(=)代入计算.
15.
解:由光的反射定律得:,,
∵,
,
,
,,
,
.
故答案为:.
根据由光的反射定律“入射角等于反射角”可得,,由平行线的性质“两直线平行,内错角相等”可得,再根据内错角相等两直线平行即可求解.
16.80°
17.(1)
(2)
(3)
18.解:①×2得:4x+2y=4 ③②+③得:7x=14
∴x=2
把x=2代入①得:y= 2
∴原方程组的解为:
本题主要考查了二元一次方程的解法,利用加减消元法:二元一次方程组的两个方程中同一未知数的系数互为相反数或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,进而求得方程组的解,即可得到答案.
19.解:如图所示,过点作,且CF与AE相交于点,则四边形ABCD即为所求作的平行四边形。
过点作,且CF与AE相交于点,进而根据平行四边形的判定定理即可求解.
20.证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥CD.(同旁内角互补,两直线平行)
∴∠BAP=∠CPA.(两直线平行,内错角相等)
∵∠1=∠2,(已知)
∴∠BAP-∠1=∠CPA-∠2
∴∠EAP=∠FPA.
∴AE∥PF.(内错角相等,两直线平行)
∴∠E=∠F.(两直线平行,内错角相等)
利用同旁内角互补,两直线平行可证得AB∥CD,利用平行线的性质可推出∠BAP=∠CPA,结合已知条件可证得∠EAP=∠FPA;再利用内错角相等,两直线平行可证得AE∥PF,然后利用平行线的性质可证得结论.
21.(1)购买240张墙贴,购买160张墙贴
(2)5
22.(1),;
(2),;
(3)
23.(1)证明:∵BC∥DF,
∴∠B+∠BFD=180°,
∵∠B=∠D,
∴∠D+∠BFD=180°,
∴AB∥CD,
∴∠A=∠ACD;
(2)解:∵∠A+∠B=108°,
∴∠ACB=72°,
∵FG∥AC,
∴∠BGF=72°,
∵BC∥DF,
∴∠EFG=72°.
(1)根据两直线平行,同旁内角互补得到∠B+∠BFD=180°,根据等量关系得到∠D+∠BFD=180°,即可得到AB∥CD证明结论;(2)利用三角形内角和定理求出∠ACB的度数,然后根据两直线平行,同位角相等求出∠BGF的度数,再根据两直线平行,内错角相等解题即可.
24.解:设矩形中较小的正方形的边长为x,较大的正方形的边长为y,
根据题意得 ,
解得,
∵b=3x+=,
∴.
设矩形中较小的正方形的边长为x,较大的正方形的边长为y,根据图形中边长之间的关系可得,求出x、y的值,再求出b=3x+=,最后求出即可.
同课章节目录
