2024-2025学年七年级下学期数学期中测试(浙江宁波市专用)(含答案)
文档属性
| 名称 | 2024-2025学年七年级下学期数学期中测试(浙江宁波市专用)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 253.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 10:31:11 | ||
图片预览




文档简介
保密★启用前
2024-2025学年七年级下册期中考试(宁波市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本大题共10小题,每小题3分,共30分.)
1.下列图案中,可以通过把一个基础图形平移得到的是( )
A. B.
C. D.
2.已知某种花粉的直径是 , 数据 0.000038 可用科学记数法表示为 ( )
A. B. C. D.
3.如图,的同位角是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.下列等式从左到右的变形,属于因式分解的是( )
A. B.
C. D.
6.若是一个完全平方式,则实数a的值为( )
A.8 B.±8 C.16 D.±16
7.在等式中,当时,;当时,,则b与c的值分别为( )
A. B.
C. D.
8.如图,是锐角的外接圆,直径平分交于于,于,连结,要求四边形面积,只需知道下列选项中某个三角形的面积,则这个三角形是( )
A. B. C. D.
9.若,,则多项式的值为( )
A. B. C. D.
10. 设 是实数, 定义@的一种运算如下: , 则下列结论: ① 若 -2 , 则 ; ②若 , 则 ;③;④a@ .其中正确的结论是( )
A.①②③④ B.①③④ C.②③ D.①②④
二、填空题(本大题共6小题,每小题3分,共18分.)
11.已知二元一次方程 + =1,用含x的代数式表示y,则y= ,用含y的代数式表示x,则x= .
12.分解因式: .
13.如图a是长方形纸带,,将纸带沿折叠成图b,再沿折叠成图c,则图c中的的度数是 .
14.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n (n是大于0的整数)个图形需要黑色棋子的个数是 .
15.若一元二次方程的两根为m,n,则的值为 .
16. 如图,,,垂足为A,交于点,点在射线上.
①若平分,则 .
②若,在直线上取一点,连接,过点作,交直线于点,若,则 .
三、解答题(本大题共8小题,第17题8分,第18题4分,第19题6分,第20题5分,第21,22题各6分,第23题7分,第24题10分,共52分.)
17.计算:
(1)
(2)
18.分解因式:
(1);
(2);
(3);
(4).
19.解方程组.
(1);
(2).
20.先化简再求值:,其中,.
21.如图,直线CD,EF交于点O,OA,OB分别平分和,且.
(1)求证:;
(2)若,求的度数.
22.成都世博会吉祥物为可爱的“桐妹儿”,寓意和平友好、包容互鉴,富有深刻的文化内涵和巴蜀特色.五一假期,小明参观完世博会后,准备购买世博会纪念品送给同学,现有A,B两款吉祥物“桐妹儿”.若购买A款吉祥物1件和B款吉祥物3件,则需190元;若购买A款吉祥物2件和B款吉祥物1件,则需180元.
(1)求每件A款吉祥物和每件B款吉祥物的价格;
(2)小明准备购买两款吉祥物共10件,若购买A款吉祥物数量为m件,购买A,B两款吉祥物总费用为W元,请写出总费用为W与数量m之间的函数关系式,并求出总费用最少为多少元?
23.如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m、宽为n的全等小矩形,且.(以上长度单位:)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,可以发现代数式可以因式分解为______;
(3)若每块小矩形的面积为,四个正方形的面积和为,试求的值.
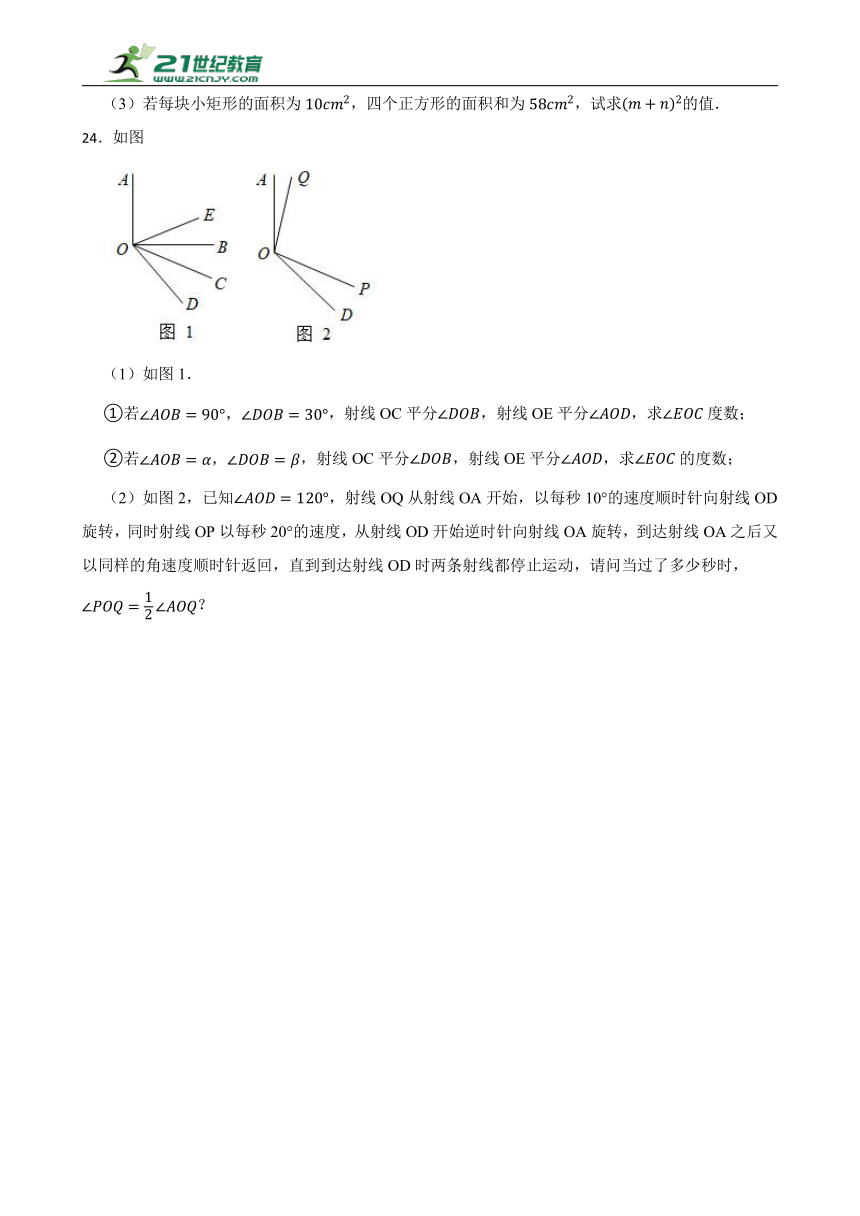
24.如图
(1)如图1.
①若,射线OC平分,射线OE平分,求度数;
②若,射线OC平分,射线OE平分,求的度数;
(2)如图2,已知,射线OQ从射线OA开始,以每秒10°的速度顺时针向射线OD旋转,同时射线OP以每秒20°的速度,从射线OD开始逆时针向射线OA旋转,到达射线OA之后又以同样的角速度顺时针返回,直到到达射线OD时两条射线都停止运动,请问当过了多少秒时,?
答案解析部分
1.C
2.C
解:0.000038=3.8x10-5.
故答案为:C.
科学记数法表示大于0小于1的数:ax10-n(1≤a<10,n为正整数).
3.B
解:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角,
根据定义,结合图形,的同位角是.
故选:B.
本题考查同位角的定义,其中同位角是指两条直线被第三条直线所截时,在截线的同旁,被截两直线的同一侧的角,据此定义进行判断,即可得到答案.
4.B
解:A、a2与a3不是同类项,不能合并,A不符合题意;
B、,B符合题意;
C、(a2b)3=a6b3,C不符合题意;
D、a2÷a3=a-1,D不符合题意.
故答案为:B.
根据合并同类项、同底数幂乘法、积的乘方、幂的乘方、同底数幂的除法法则进行化简即可.
5.D
6.D
解:∵是一个完全平方式,16=;
∴,解得a=16或-16.
故答案为:D.
完全平方式有两种和,代数式如果系数不为1,先提取二次项的系数,根据一次项系数等于±2ab来计算即可.
7.A
8.C
9.A
10.A
解:①∵a@b=1+( 2)+1×( 2)= 3,∴①正确.
②∵ 2@x= 2+x+( 2)x= 2 x= 3,解得x=1,∴②正确.
③∵a@b=a+b+ab b@a=b+a+ab,∴a@b=b@a,∴③正确.
④∵a@(b@c)=a@(b+c+bc)=a+(b+c+bc)+a(b+c+bc)=a+b+c+bc+ab+ac+abc,
(a@b)@c=(a+b+ab)@c=(a+b+ab)+c+(a+b+ab)c=a+b+c+bc+ab+ac+abc,
∴a@(b@c)=(a@b)@c,∴④正确.
综上,正确的结论是①②③④,
故答案为:A.
利用题干中的定义及计算方法逐项分析判断即可.
11.;4-2y
解:∵ + =1
等号两边均乘4得x+2y=4,
∴y=,x=4-2y.
故答案为: , 4-2y .
根据移项、系数化为1,分别用含x的代数式表示y和用含y的代数式表示x,即可解答.
12.
解: ;
故答案为 .
先提取公因式5,再利用平方差公式因式分解即可。
13.126°
14.n2+2n
15.6
16.;或
解:①如图所示:
∵PQ//MN,l⊥MN,
∴∠ABP=∠BAM=90°,
∴∠PBC=∠PBA=45°,
∵PQ//MN,
∴∠PBC+∠BCM=180°,
∴∠BCM=135°;
故答案为:135°;
②分两种情况,
1)如图所示:
∵∠BDE=30°,CD⊥DE,
∴∠CDB=60°,
∵PQ//MN,
∴∠ACD+∠CDB=180°,
∴∠ACD=180°-60°=120°;
2)如图所示:
∵∠BDE=30°,CD⊥DE,
∴∠BDC=∠BDE+∠CDE=120°,
∵PQ//MN,
∴∠BDC+∠ACD=180°,
∴∠ACD=60°,
综上所述:∠ACD=60°或120°,
故答案为:60°或120°。
①根据题意求出∠ABP=∠BAM=90°,再根据平行线的性质求出∠ACD+∠CDB=180°,最后计算求解即可;
②分类讨论,先作图,再根据平行线的性质计算求解即可。
17.(1)
(2)
18.(1)
(2)
(3)
(4)
19.(1)解:将代入,得,
解得,
将代入,
解得,
方程组的解为
(2)解:将整理,可,
将与相加,
可得,
解得,
代入后得,
解得,
∴方程组的解为
(1)利用代入消元法解二元一次方程组即可;
(2)先去分母整理,然后根据加减消元法解二元一次方程组.
20.解:化简得:
把a,b的值代入原式
【解得】解:
=
=
=3a-2b
把a,b的值代入原式=
根据完全平方公式和平方差公式化简括号内,再根据多项式除以单项式化简,再代入a,b值即可求出答案.
21.(1)证明:OA,OB分别平分和,
.
.
.
,
.
.
.
(2)解:平分,,
.
设,则.
,
即,
解得
.
(1)由角平分线的定义,结合平角的定义得出∠AOC+∠BOE=90°,根据同位角相等,两直线平行证明AB∥CD,由平行线的性质,结合等量代换,证明即可.
(2)由角平分线的定义和平行线的性质得出∠BOD=∠2=∠BOG,设∠2=x,则∠3=3∠2=3x.根据平角的定义建立方程,据此求解.
22.(1)每件A款吉祥物的价格是70元,每件B款吉祥物的价格是40元;
(2)总费用为W与数量m之间的函数关系式为,总费用最少为520元.
23.(1)
(2)
(3)49
24.(1)解:①∵,
∴,
∵射线平分,射线平分,
∴,
∴;
②∵,
∴,
∵射线平分,射线平分,
∴,
∴
(2)解:秒.
设t秒后,
当向运动,且与相遇前,由题意得
,
解得;
当向运动,且与相遇后,由题意得
,
解得:
当向运动,追上前,由题意得
解得,;
当向运动,追上后,由题意得,
,
解得:(不合题意,舍去);
答:当过了秒或秒或秒时,
(1)①由题图可知,利用角平分线的定义可得,,求出和的度数,再利用即可求解;
②将 分别代入①中的式子计算即可;
(2)先用 的度数除以OD每秒旋转的度数,求出OD运动的时间,再设经过t秒后,最后分以下几种情况分别列方程求解即可:当向运动,且与相遇前,由题意得;当向运动,且与相遇后,由题意得;当向运动,追上前,由题意得;当向运动,追上后,由题意得,,最后选择解中t小于或等于OD运动的时间的即为答案.
2024-2025学年七年级下册期中考试(宁波市专用)
数学
考试范围:浙教版七下第一章-第三章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本大题共10小题,每小题3分,共30分.)
1.下列图案中,可以通过把一个基础图形平移得到的是( )
A. B.
C. D.
2.已知某种花粉的直径是 , 数据 0.000038 可用科学记数法表示为 ( )
A. B. C. D.
3.如图,的同位角是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.下列等式从左到右的变形,属于因式分解的是( )
A. B.
C. D.
6.若是一个完全平方式,则实数a的值为( )
A.8 B.±8 C.16 D.±16
7.在等式中,当时,;当时,,则b与c的值分别为( )
A. B.
C. D.
8.如图,是锐角的外接圆,直径平分交于于,于,连结,要求四边形面积,只需知道下列选项中某个三角形的面积,则这个三角形是( )
A. B. C. D.
9.若,,则多项式的值为( )
A. B. C. D.
10. 设 是实数, 定义@的一种运算如下: , 则下列结论: ① 若 -2 , 则 ; ②若 , 则 ;③;④a@ .其中正确的结论是( )
A.①②③④ B.①③④ C.②③ D.①②④
二、填空题(本大题共6小题,每小题3分,共18分.)
11.已知二元一次方程 + =1,用含x的代数式表示y,则y= ,用含y的代数式表示x,则x= .
12.分解因式: .
13.如图a是长方形纸带,,将纸带沿折叠成图b,再沿折叠成图c,则图c中的的度数是 .
14.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n (n是大于0的整数)个图形需要黑色棋子的个数是 .
15.若一元二次方程的两根为m,n,则的值为 .
16. 如图,,,垂足为A,交于点,点在射线上.
①若平分,则 .
②若,在直线上取一点,连接,过点作,交直线于点,若,则 .
三、解答题(本大题共8小题,第17题8分,第18题4分,第19题6分,第20题5分,第21,22题各6分,第23题7分,第24题10分,共52分.)
17.计算:
(1)
(2)
18.分解因式:
(1);
(2);
(3);
(4).
19.解方程组.
(1);
(2).
20.先化简再求值:,其中,.
21.如图,直线CD,EF交于点O,OA,OB分别平分和,且.
(1)求证:;
(2)若,求的度数.
22.成都世博会吉祥物为可爱的“桐妹儿”,寓意和平友好、包容互鉴,富有深刻的文化内涵和巴蜀特色.五一假期,小明参观完世博会后,准备购买世博会纪念品送给同学,现有A,B两款吉祥物“桐妹儿”.若购买A款吉祥物1件和B款吉祥物3件,则需190元;若购买A款吉祥物2件和B款吉祥物1件,则需180元.
(1)求每件A款吉祥物和每件B款吉祥物的价格;
(2)小明准备购买两款吉祥物共10件,若购买A款吉祥物数量为m件,购买A,B两款吉祥物总费用为W元,请写出总费用为W与数量m之间的函数关系式,并求出总费用最少为多少元?
23.如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m、宽为n的全等小矩形,且.(以上长度单位:)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,可以发现代数式可以因式分解为______;
(3)若每块小矩形的面积为,四个正方形的面积和为,试求的值.
24.如图
(1)如图1.
①若,射线OC平分,射线OE平分,求度数;
②若,射线OC平分,射线OE平分,求的度数;
(2)如图2,已知,射线OQ从射线OA开始,以每秒10°的速度顺时针向射线OD旋转,同时射线OP以每秒20°的速度,从射线OD开始逆时针向射线OA旋转,到达射线OA之后又以同样的角速度顺时针返回,直到到达射线OD时两条射线都停止运动,请问当过了多少秒时,?
答案解析部分
1.C
2.C
解:0.000038=3.8x10-5.
故答案为:C.
科学记数法表示大于0小于1的数:ax10-n(1≤a<10,n为正整数).
3.B
解:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角,
根据定义,结合图形,的同位角是.
故选:B.
本题考查同位角的定义,其中同位角是指两条直线被第三条直线所截时,在截线的同旁,被截两直线的同一侧的角,据此定义进行判断,即可得到答案.
4.B
解:A、a2与a3不是同类项,不能合并,A不符合题意;
B、,B符合题意;
C、(a2b)3=a6b3,C不符合题意;
D、a2÷a3=a-1,D不符合题意.
故答案为:B.
根据合并同类项、同底数幂乘法、积的乘方、幂的乘方、同底数幂的除法法则进行化简即可.
5.D
6.D
解:∵是一个完全平方式,16=;
∴,解得a=16或-16.
故答案为:D.
完全平方式有两种和,代数式如果系数不为1,先提取二次项的系数,根据一次项系数等于±2ab来计算即可.
7.A
8.C
9.A
10.A
解:①∵a@b=1+( 2)+1×( 2)= 3,∴①正确.
②∵ 2@x= 2+x+( 2)x= 2 x= 3,解得x=1,∴②正确.
③∵a@b=a+b+ab b@a=b+a+ab,∴a@b=b@a,∴③正确.
④∵a@(b@c)=a@(b+c+bc)=a+(b+c+bc)+a(b+c+bc)=a+b+c+bc+ab+ac+abc,
(a@b)@c=(a+b+ab)@c=(a+b+ab)+c+(a+b+ab)c=a+b+c+bc+ab+ac+abc,
∴a@(b@c)=(a@b)@c,∴④正确.
综上,正确的结论是①②③④,
故答案为:A.
利用题干中的定义及计算方法逐项分析判断即可.
11.;4-2y
解:∵ + =1
等号两边均乘4得x+2y=4,
∴y=,x=4-2y.
故答案为: , 4-2y .
根据移项、系数化为1,分别用含x的代数式表示y和用含y的代数式表示x,即可解答.
12.
解: ;
故答案为 .
先提取公因式5,再利用平方差公式因式分解即可。
13.126°
14.n2+2n
15.6
16.;或
解:①如图所示:
∵PQ//MN,l⊥MN,
∴∠ABP=∠BAM=90°,
∴∠PBC=∠PBA=45°,
∵PQ//MN,
∴∠PBC+∠BCM=180°,
∴∠BCM=135°;
故答案为:135°;
②分两种情况,
1)如图所示:
∵∠BDE=30°,CD⊥DE,
∴∠CDB=60°,
∵PQ//MN,
∴∠ACD+∠CDB=180°,
∴∠ACD=180°-60°=120°;
2)如图所示:
∵∠BDE=30°,CD⊥DE,
∴∠BDC=∠BDE+∠CDE=120°,
∵PQ//MN,
∴∠BDC+∠ACD=180°,
∴∠ACD=60°,
综上所述:∠ACD=60°或120°,
故答案为:60°或120°。
①根据题意求出∠ABP=∠BAM=90°,再根据平行线的性质求出∠ACD+∠CDB=180°,最后计算求解即可;
②分类讨论,先作图,再根据平行线的性质计算求解即可。
17.(1)
(2)
18.(1)
(2)
(3)
(4)
19.(1)解:将代入,得,
解得,
将代入,
解得,
方程组的解为
(2)解:将整理,可,
将与相加,
可得,
解得,
代入后得,
解得,
∴方程组的解为
(1)利用代入消元法解二元一次方程组即可;
(2)先去分母整理,然后根据加减消元法解二元一次方程组.
20.解:化简得:
把a,b的值代入原式
【解得】解:
=
=
=3a-2b
把a,b的值代入原式=
根据完全平方公式和平方差公式化简括号内,再根据多项式除以单项式化简,再代入a,b值即可求出答案.
21.(1)证明:OA,OB分别平分和,
.
.
.
,
.
.
.
(2)解:平分,,
.
设,则.
,
即,
解得
.
(1)由角平分线的定义,结合平角的定义得出∠AOC+∠BOE=90°,根据同位角相等,两直线平行证明AB∥CD,由平行线的性质,结合等量代换,证明即可.
(2)由角平分线的定义和平行线的性质得出∠BOD=∠2=∠BOG,设∠2=x,则∠3=3∠2=3x.根据平角的定义建立方程,据此求解.
22.(1)每件A款吉祥物的价格是70元,每件B款吉祥物的价格是40元;
(2)总费用为W与数量m之间的函数关系式为,总费用最少为520元.
23.(1)
(2)
(3)49
24.(1)解:①∵,
∴,
∵射线平分,射线平分,
∴,
∴;
②∵,
∴,
∵射线平分,射线平分,
∴,
∴
(2)解:秒.
设t秒后,
当向运动,且与相遇前,由题意得
,
解得;
当向运动,且与相遇后,由题意得
,
解得:
当向运动,追上前,由题意得
解得,;
当向运动,追上后,由题意得,
,
解得:(不合题意,舍去);
答:当过了秒或秒或秒时,
(1)①由题图可知,利用角平分线的定义可得,,求出和的度数,再利用即可求解;
②将 分别代入①中的式子计算即可;
(2)先用 的度数除以OD每秒旋转的度数,求出OD运动的时间,再设经过t秒后,最后分以下几种情况分别列方程求解即可:当向运动,且与相遇前,由题意得;当向运动,且与相遇后,由题意得;当向运动,追上前,由题意得;当向运动,追上后,由题意得,,最后选择解中t小于或等于OD运动的时间的即为答案.
同课章节目录
