2024-2025学年七年级下学期数学期中测试(广东省深圳市专用)(含答案)
文档属性
| 名称 | 2024-2025学年七年级下学期数学期中测试(广东省深圳市专用)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 399.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
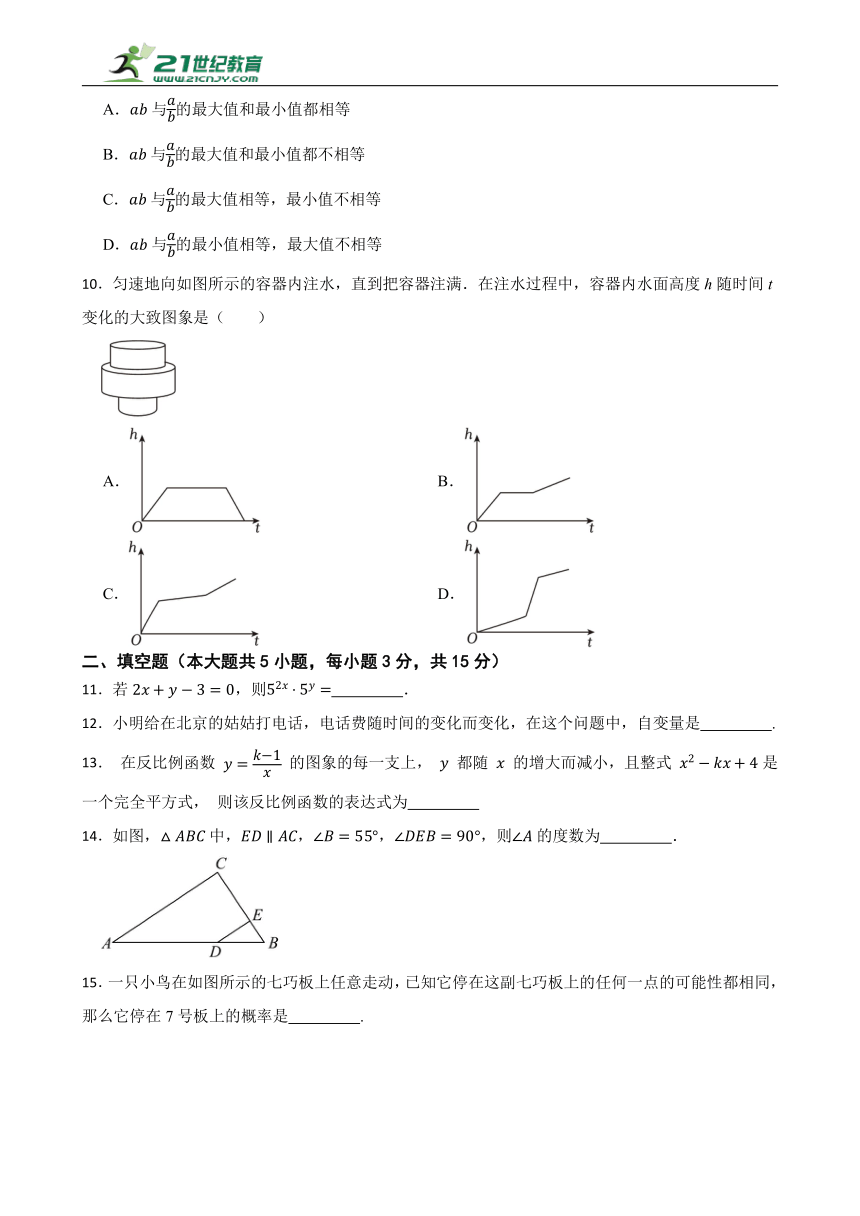
| 科目 | 数学 | ||
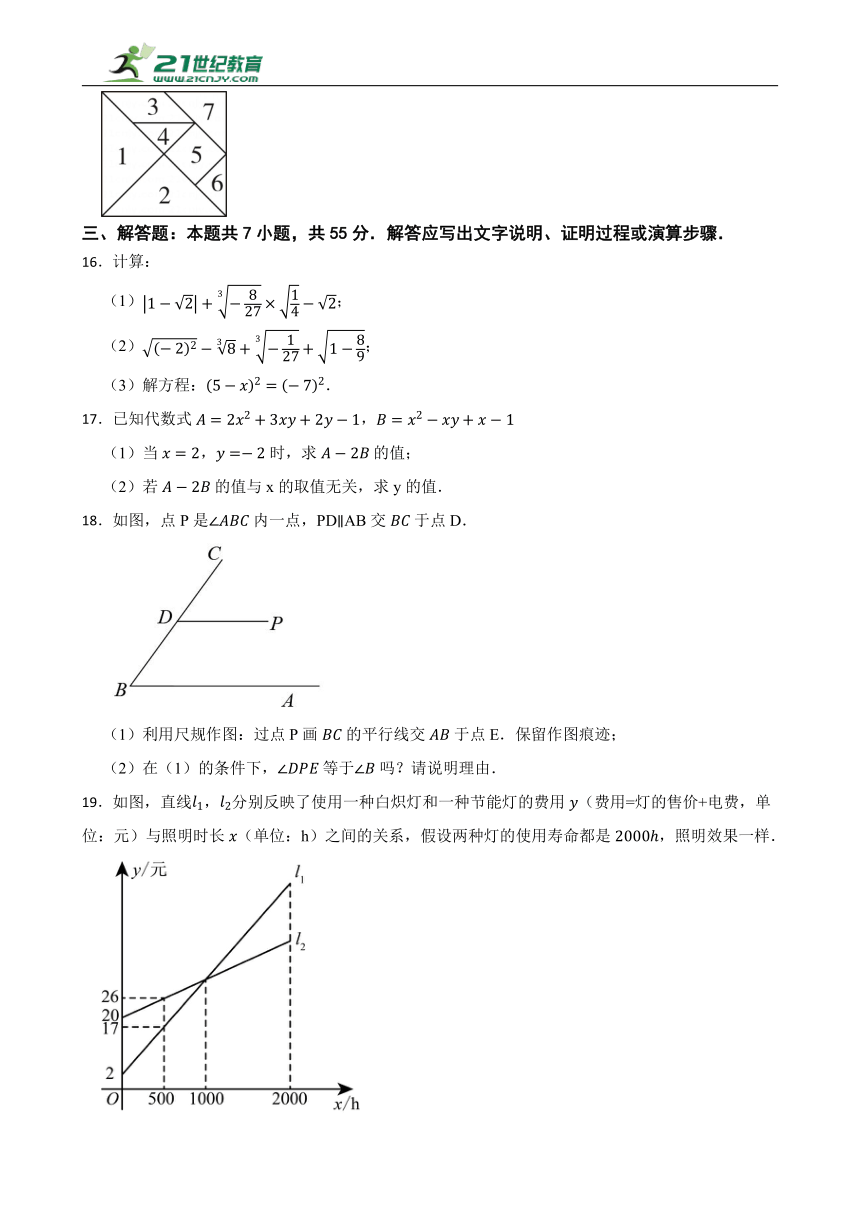
| 更新时间 | 2025-03-29 10:48:37 | ||
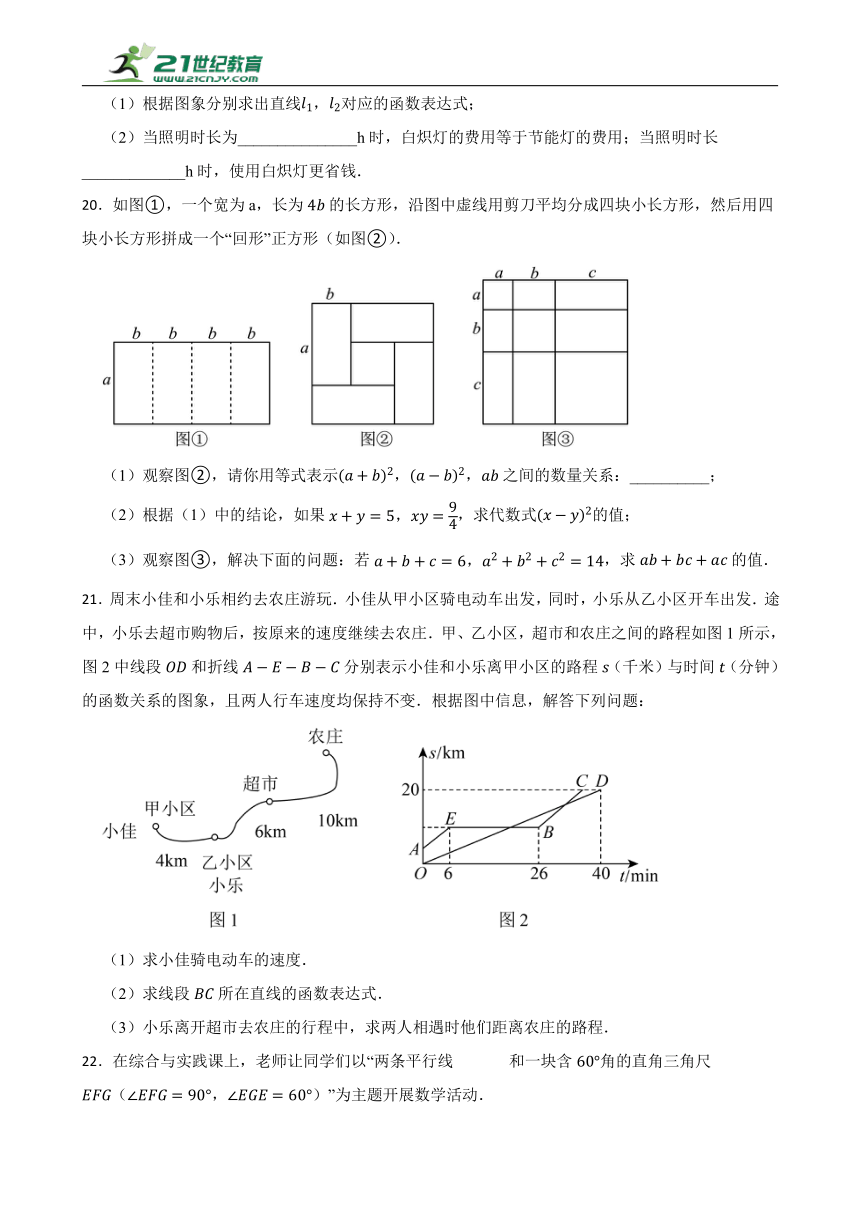
图片预览

文档简介
保密★启用前
2024-2025学年七级下册期中考试(深圳市专用)
数学
考试范围:北师大版七下第1章-第4章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题:本大题共10小题,每小题3分,共30分.每小题只有一个选项符合题目要求.
1.将一副三角尺按如下列各图所示的不同位置摆放,其中与一定互余的摆放方式是( )
A. B.
C. D.
2.2024年的新型医疗检测设备可以检测到血液中极低浓度的疾病标志物,例如能够检测到每毫升血液中克的某种特定蛋白质,请将用科学记数法表示为( )
A. B. C. D.
3.下列命题中,是真命题的是( )
A.同旁内角互补
B.相等的角是对顶角
C.经过直线外一点,有无数条直线与这条直线平行
D.两点之间,线段最短
4.下列运算正确的是( )
A. B.
C. D.
5.已知,,则多项式的值为( )
A. B. C. D.
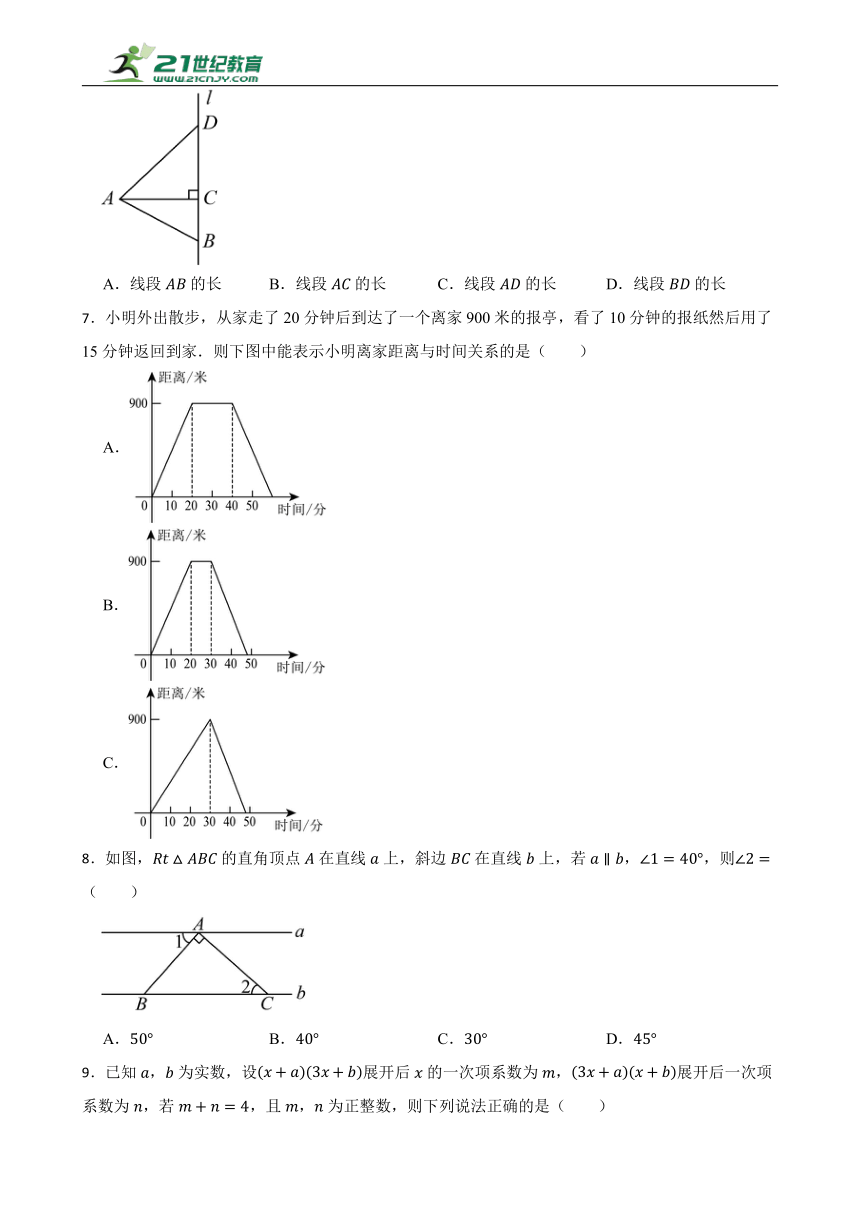
6.如图,点A是直线l外一点,点B,C,D在直线l上,连接,若,则点A到直线l的距离是( ).
A.线段的长 B.线段的长 C.线段的长 D.线段的长
7.小明外出散步,从家走了20分钟后到达了一个离家900米的报亭,看了10分钟的报纸然后用了15分钟返回到家.则下图中能表示小明离家距离与时间关系的是( )
A.
B.
C.
8.如图,的直角顶点在直线上,斜边在直线上,若,,则( )
A. B. C. D.
9.已知,为实数,设展开后的一次项系数为,展开后一次项系数为,若,且,为正整数,则下列说法正确的是( )
A.与的最大值和最小值都相等
B.与的最大值和最小值都不相等
C.与的最大值相等,最小值不相等
D.与的最小值相等,最大值不相等
10.匀速地向如图所示的容器内注水,直到把容器注满.在注水过程中,容器内水面高度h随时间t变化的大致图象是( )
A. B.
C. D.
二、填空题(本大题共5小题,每小题3分,共15分)
11.若,则 .
12.小明给在北京的姑姑打电话,电话费随时间的变化而变化,在这个问题中,自变量是 .
13. 在反比例函数 的图象的每一支上, 都随 的增大而减小,且整式 是一个完全平方式, 则该反比例函数的表达式为
14.如图,中,,,,则的度数为 .
15.一只小鸟在如图所示的七巧板上任意走动,已知它停在这副七巧板上的任何一点的可能性都相同,那么它停在7号板上的概率是 .
三、解答题:本题共7小题,共55分.解答应写出文字说明、证明过程或演算步骤.
16.计算:
(1);
(2);
(3)解方程:.
17.已知代数式,
(1)当,时,求的值;
(2)若的值与x的取值无关,求y的值.
18.如图,点P是内一点,PDAB交于点D.
(1)利用尺规作图:过点P画的平行线交于点E.保留作图痕迹;
(2)在(1)的条件下,等于吗?请说明理由.
19.如图,直线,分别反映了使用一种白炽灯和一种节能灯的费用(费用=灯的售价+电费,单位:元)与照明时长(单位:h)之间的关系,假设两种灯的使用寿命都是,照明效果一样.
(1)根据图象分别求出直线,对应的函数表达式;
(2)当照明时长为_______________h时,白炽灯的费用等于节能灯的费用;当照明时长_____________h时,使用白炽灯更省钱.
20.如图①,一个宽为a,长为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②).
(1)观察图②,请你用等式表示,,之间的数量关系:__________;
(2)根据(1)中的结论,如果,求代数式的值;
(3)观察图③,解决下面的问题:若,求的值.
21.周末小佳和小乐相约去农庄游玩.小佳从甲小区骑电动车出发,同时,小乐从乙小区开车出发.途中,小乐去超市购物后,按原来的速度继续去农庄.甲、乙小区,超市和农庄之间的路程如图1所示,图2中线段和折线分别表示小佳和小乐离甲小区的路程(千米)与时间(分钟)的函数关系的图象,且两人行车速度均保持不变.根据图中信息,解答下列问题:
(1)求小佳骑电动车的速度.
(2)求线段所在直线的函数表达式.
(3)小乐离开超市去农庄的行程中,求两人相遇时他们距离农庄的路程.
22.在综合与实践课上,老师让同学们以“两条平行线 和一块含角的直角三角尺(,)”为主题开展数学活动.
(1)如图1,三角尺的角的顶点G在上.若,则的度数为 .
(2)如图2,小颖把三角尺的两个锐角的顶点E,G分别放在和上,请你探索与之间的数量关系.
(3)如图3,小亮把三角尺的直角顶点F放在上,角的顶点E在上.若,,请直接写出与的数量关系(用含,的式子表示)
答案解析部分
1.C
2.D
3.D
解:A中,两直线平行,同旁内角互补,是假命题,故A不符合题意;
B中,相等的角不一定是对顶角,比如两直线平行,同位角相等,所以是假命题,故B不符合题意;
C中,经过直线外一点,有且只有一条直线与这条直线平行,是假命题,故C不符合题意;
D中,两点之间,线段最短,是真命题,故D符合题意;
故选:D.
本题主要考查命题、平行线的性质及线段,如果命题的题设成立,那么结论一定成立,结合选项,逐项分析判断,即可得到答案.
4.C
5.B
6.B
7.B
8.A
9.D
10.C
解:观察图形,该容器有半径各不相同的三个圆柱组成,最下面的圆柱半径最小,故水面高度上升的最快;中间的圆柱半径最大,故水面高度上升最慢;
故容器内水面高度h随时间t变化的大致图象是:
故答案为:C.
根据容器的组成可知最下面圆柱半径最小,中间圆柱半径最大,故注水过程水的高度变化速度先快后慢再快,即可判断答案.
11.125
解:∵,
∴,
∴.
故答案为:125.
由已知条件得,举哀那个待求式子利用同底数幂的乘法的法则“同底数幂相乘,底数不变,指数相加”进行运算后整体代入,最后按有理数的乘方运算法则计算即可.
12.时间
解:小明给在北京的姑姑打电话,电话费随时间的变化而变化,在这个问题中,自变量是时间,因变量是电话费.
故答案为:时间.
函数的定义:设x和y是两个变量,对于x的每一个值,y都有唯一确定的值和它对应,则x是自变量,y是x的函数,也叫因变量,据此并由“电话费随时间的变化而变化”可得出答案.
13.=
解:∵反比例函数的性质:
当k>0时,双曲线的两支分别在一、三象限,在每一个象限内,y随x的增大而减小
当k<0时,双曲线的两支分别在二、四象限,在每一个象限内,y随x的增大而增大
∴k-1>0
∴k>1
又∵是 一个完全平方式
∴k=±4
∴k=4
∴ 反比例函数的表达式为=
故答案为:=.
根据反比例函数的性质:当k>0时,双曲线的两支分别在一、三象限,在每一个象限内,y随x的增大而减小;当k<0时,双曲线的两支分别在二、四象限,在每一个象限内,y随x的增大而增大可得k的范围,再根据 是 一个完全平方式可得k的值,代入可得反比例函数解析式.
14.
15.
解:设正方形边长为1,则其面积为1,
根据题意分析可知:7号板是等腰直角三角形,面积为,
故它最终停留在7号板上的概率是,
故答案为:.
设正方形边长为1,则其面积为1,再求出7号板的面积即可得出答案.
16.(1)解:
;
(2)解:
;
(3)解:,
,
,
.
(1)根据绝对值得意义,开立方运算:算术平方根化简以后计算计算;
(2)利用算术平方根得性质、立方根,,化简后计算即可;
(3)先计算,在用开方运算转化为两个一元一次方程即可求解.
(1)解:
;
(2)
;
(3),
,
,
.
17.(1)
(2)
18.(1)解:如图,即为所求;
(2)解:,理由如下:∵(已知)
∴(两直线平行,同位角相等)
由(1)知:
∴(等量代换).
(1)根据平行线的尺规作图方法, 过点P画的平行线交于点E ,即可求解;
(2)由,根据平行线的同位角相等,得到,结合,即可证得.
19.(1);
(2),
20.(1)
(2)解:由(1)可知,
∴;
(3)解:各部分的面积如图所示,
由图可得,
∴;
∴.
解:(1)∵图2的面积可由大正方形的面积求出:,还可由四个长方形的面积+中间小正方形的面积求出:,
∴可得出等式.
故答案为:;
(1)图2的面积可由大正方形的面积求出,还可由四个长方形的面积+中间小正方形的面积求出,即可得出等式;
(2)将各代数式的值对应代入(1)中的代数式求解即可;
(3)在图③中标出各部分的面积,由图大正方形的面积求出:,还可以表示为各个部分的面积之和,列出各面积大小关系的代数式,再代值进行求解即可.
(1)解:∵图2的面积可由大正方形的面积求出:,
还可由四个长方形的面积+中间小正方形的面积求出:,
∴可得出等式.
故答案为:;
(2)解:由(1)可知,
∴;
(3)解:各部分的面积如图所示,
由图可得,
∴,
∴.
21.(1)
(2);
(3)
22.(1)
(2)
(3)
2024-2025学年七级下册期中考试(深圳市专用)
数学
考试范围:北师大版七下第1章-第4章 考试时间:100分钟 分值;120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题:本大题共10小题,每小题3分,共30分.每小题只有一个选项符合题目要求.
1.将一副三角尺按如下列各图所示的不同位置摆放,其中与一定互余的摆放方式是( )
A. B.
C. D.
2.2024年的新型医疗检测设备可以检测到血液中极低浓度的疾病标志物,例如能够检测到每毫升血液中克的某种特定蛋白质,请将用科学记数法表示为( )
A. B. C. D.
3.下列命题中,是真命题的是( )
A.同旁内角互补
B.相等的角是对顶角
C.经过直线外一点,有无数条直线与这条直线平行
D.两点之间,线段最短
4.下列运算正确的是( )
A. B.
C. D.
5.已知,,则多项式的值为( )
A. B. C. D.
6.如图,点A是直线l外一点,点B,C,D在直线l上,连接,若,则点A到直线l的距离是( ).
A.线段的长 B.线段的长 C.线段的长 D.线段的长
7.小明外出散步,从家走了20分钟后到达了一个离家900米的报亭,看了10分钟的报纸然后用了15分钟返回到家.则下图中能表示小明离家距离与时间关系的是( )
A.
B.
C.
8.如图,的直角顶点在直线上,斜边在直线上,若,,则( )
A. B. C. D.
9.已知,为实数,设展开后的一次项系数为,展开后一次项系数为,若,且,为正整数,则下列说法正确的是( )
A.与的最大值和最小值都相等
B.与的最大值和最小值都不相等
C.与的最大值相等,最小值不相等
D.与的最小值相等,最大值不相等
10.匀速地向如图所示的容器内注水,直到把容器注满.在注水过程中,容器内水面高度h随时间t变化的大致图象是( )
A. B.
C. D.
二、填空题(本大题共5小题,每小题3分,共15分)
11.若,则 .
12.小明给在北京的姑姑打电话,电话费随时间的变化而变化,在这个问题中,自变量是 .
13. 在反比例函数 的图象的每一支上, 都随 的增大而减小,且整式 是一个完全平方式, 则该反比例函数的表达式为
14.如图,中,,,,则的度数为 .
15.一只小鸟在如图所示的七巧板上任意走动,已知它停在这副七巧板上的任何一点的可能性都相同,那么它停在7号板上的概率是 .
三、解答题:本题共7小题,共55分.解答应写出文字说明、证明过程或演算步骤.
16.计算:
(1);
(2);
(3)解方程:.
17.已知代数式,
(1)当,时,求的值;
(2)若的值与x的取值无关,求y的值.
18.如图,点P是内一点,PDAB交于点D.
(1)利用尺规作图:过点P画的平行线交于点E.保留作图痕迹;
(2)在(1)的条件下,等于吗?请说明理由.
19.如图,直线,分别反映了使用一种白炽灯和一种节能灯的费用(费用=灯的售价+电费,单位:元)与照明时长(单位:h)之间的关系,假设两种灯的使用寿命都是,照明效果一样.
(1)根据图象分别求出直线,对应的函数表达式;
(2)当照明时长为_______________h时,白炽灯的费用等于节能灯的费用;当照明时长_____________h时,使用白炽灯更省钱.
20.如图①,一个宽为a,长为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②).
(1)观察图②,请你用等式表示,,之间的数量关系:__________;
(2)根据(1)中的结论,如果,求代数式的值;
(3)观察图③,解决下面的问题:若,求的值.
21.周末小佳和小乐相约去农庄游玩.小佳从甲小区骑电动车出发,同时,小乐从乙小区开车出发.途中,小乐去超市购物后,按原来的速度继续去农庄.甲、乙小区,超市和农庄之间的路程如图1所示,图2中线段和折线分别表示小佳和小乐离甲小区的路程(千米)与时间(分钟)的函数关系的图象,且两人行车速度均保持不变.根据图中信息,解答下列问题:
(1)求小佳骑电动车的速度.
(2)求线段所在直线的函数表达式.
(3)小乐离开超市去农庄的行程中,求两人相遇时他们距离农庄的路程.
22.在综合与实践课上,老师让同学们以“两条平行线 和一块含角的直角三角尺(,)”为主题开展数学活动.
(1)如图1,三角尺的角的顶点G在上.若,则的度数为 .
(2)如图2,小颖把三角尺的两个锐角的顶点E,G分别放在和上,请你探索与之间的数量关系.
(3)如图3,小亮把三角尺的直角顶点F放在上,角的顶点E在上.若,,请直接写出与的数量关系(用含,的式子表示)
答案解析部分
1.C
2.D
3.D
解:A中,两直线平行,同旁内角互补,是假命题,故A不符合题意;
B中,相等的角不一定是对顶角,比如两直线平行,同位角相等,所以是假命题,故B不符合题意;
C中,经过直线外一点,有且只有一条直线与这条直线平行,是假命题,故C不符合题意;
D中,两点之间,线段最短,是真命题,故D符合题意;
故选:D.
本题主要考查命题、平行线的性质及线段,如果命题的题设成立,那么结论一定成立,结合选项,逐项分析判断,即可得到答案.
4.C
5.B
6.B
7.B
8.A
9.D
10.C
解:观察图形,该容器有半径各不相同的三个圆柱组成,最下面的圆柱半径最小,故水面高度上升的最快;中间的圆柱半径最大,故水面高度上升最慢;
故容器内水面高度h随时间t变化的大致图象是:
故答案为:C.
根据容器的组成可知最下面圆柱半径最小,中间圆柱半径最大,故注水过程水的高度变化速度先快后慢再快,即可判断答案.
11.125
解:∵,
∴,
∴.
故答案为:125.
由已知条件得,举哀那个待求式子利用同底数幂的乘法的法则“同底数幂相乘,底数不变,指数相加”进行运算后整体代入,最后按有理数的乘方运算法则计算即可.
12.时间
解:小明给在北京的姑姑打电话,电话费随时间的变化而变化,在这个问题中,自变量是时间,因变量是电话费.
故答案为:时间.
函数的定义:设x和y是两个变量,对于x的每一个值,y都有唯一确定的值和它对应,则x是自变量,y是x的函数,也叫因变量,据此并由“电话费随时间的变化而变化”可得出答案.
13.=
解:∵反比例函数的性质:
当k>0时,双曲线的两支分别在一、三象限,在每一个象限内,y随x的增大而减小
当k<0时,双曲线的两支分别在二、四象限,在每一个象限内,y随x的增大而增大
∴k-1>0
∴k>1
又∵是 一个完全平方式
∴k=±4
∴k=4
∴ 反比例函数的表达式为=
故答案为:=.
根据反比例函数的性质:当k>0时,双曲线的两支分别在一、三象限,在每一个象限内,y随x的增大而减小;当k<0时,双曲线的两支分别在二、四象限,在每一个象限内,y随x的增大而增大可得k的范围,再根据 是 一个完全平方式可得k的值,代入可得反比例函数解析式.
14.
15.
解:设正方形边长为1,则其面积为1,
根据题意分析可知:7号板是等腰直角三角形,面积为,
故它最终停留在7号板上的概率是,
故答案为:.
设正方形边长为1,则其面积为1,再求出7号板的面积即可得出答案.
16.(1)解:
;
(2)解:
;
(3)解:,
,
,
.
(1)根据绝对值得意义,开立方运算:算术平方根化简以后计算计算;
(2)利用算术平方根得性质、立方根,,化简后计算即可;
(3)先计算,在用开方运算转化为两个一元一次方程即可求解.
(1)解:
;
(2)
;
(3),
,
,
.
17.(1)
(2)
18.(1)解:如图,即为所求;
(2)解:,理由如下:∵(已知)
∴(两直线平行,同位角相等)
由(1)知:
∴(等量代换).
(1)根据平行线的尺规作图方法, 过点P画的平行线交于点E ,即可求解;
(2)由,根据平行线的同位角相等,得到,结合,即可证得.
19.(1);
(2),
20.(1)
(2)解:由(1)可知,
∴;
(3)解:各部分的面积如图所示,
由图可得,
∴;
∴.
解:(1)∵图2的面积可由大正方形的面积求出:,还可由四个长方形的面积+中间小正方形的面积求出:,
∴可得出等式.
故答案为:;
(1)图2的面积可由大正方形的面积求出,还可由四个长方形的面积+中间小正方形的面积求出,即可得出等式;
(2)将各代数式的值对应代入(1)中的代数式求解即可;
(3)在图③中标出各部分的面积,由图大正方形的面积求出:,还可以表示为各个部分的面积之和,列出各面积大小关系的代数式,再代值进行求解即可.
(1)解:∵图2的面积可由大正方形的面积求出:,
还可由四个长方形的面积+中间小正方形的面积求出:,
∴可得出等式.
故答案为:;
(2)解:由(1)可知,
∴;
(3)解:各部分的面积如图所示,
由图可得,
∴,
∴.
21.(1)
(2);
(3)
22.(1)
(2)
(3)
同课章节目录
