第四单元专项练习05:正比例和反比例的意义与图像应用-2024-2025学年六年级数学下册典型例题(人教版)(含解析)
文档属性
| 名称 | 第四单元专项练习05:正比例和反比例的意义与图像应用-2024-2025学年六年级数学下册典型例题(人教版)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览


文档简介
/ 让教学更有效 精品试卷 | 数学学科
第四单元专项练习05:正比例和反比例的意义与图像应用
1.如下图表示一工程队修筑公路的长度与所用时间的关系,这个工程队修路长度与所用时间成( )比例,照这样计算,修长750米公路需要( )天。
2.下图表示一辆汽车行驶的路程和耗油量之间的关系。汽车行驶的路程和耗油量成( )比例,汽车行驶20千米,耗油( )升。
3.科学小组的同学做实验,在弹簧的弹性限度内,所挂物体的质量与弹簧伸长的长度情况如下表:
物体质量(kg) 0 1 2 3 4 5 6 … 10
弹簧伸长长度(cm) 0 0.5 1 1.5 2 2.5 3 5
根据科学小组测量的数据,在弹簧的弹性限度内,所挂物体的质量与弹簧伸长的长度成( )比例关系,在下面简要说明理由:( )。
4.如表中m和n是两个相关联的量。
(1)当时,m与n成( )比例关系。
m 6 x
n 3
(2)当x=( )时,m与n成反比例关系。
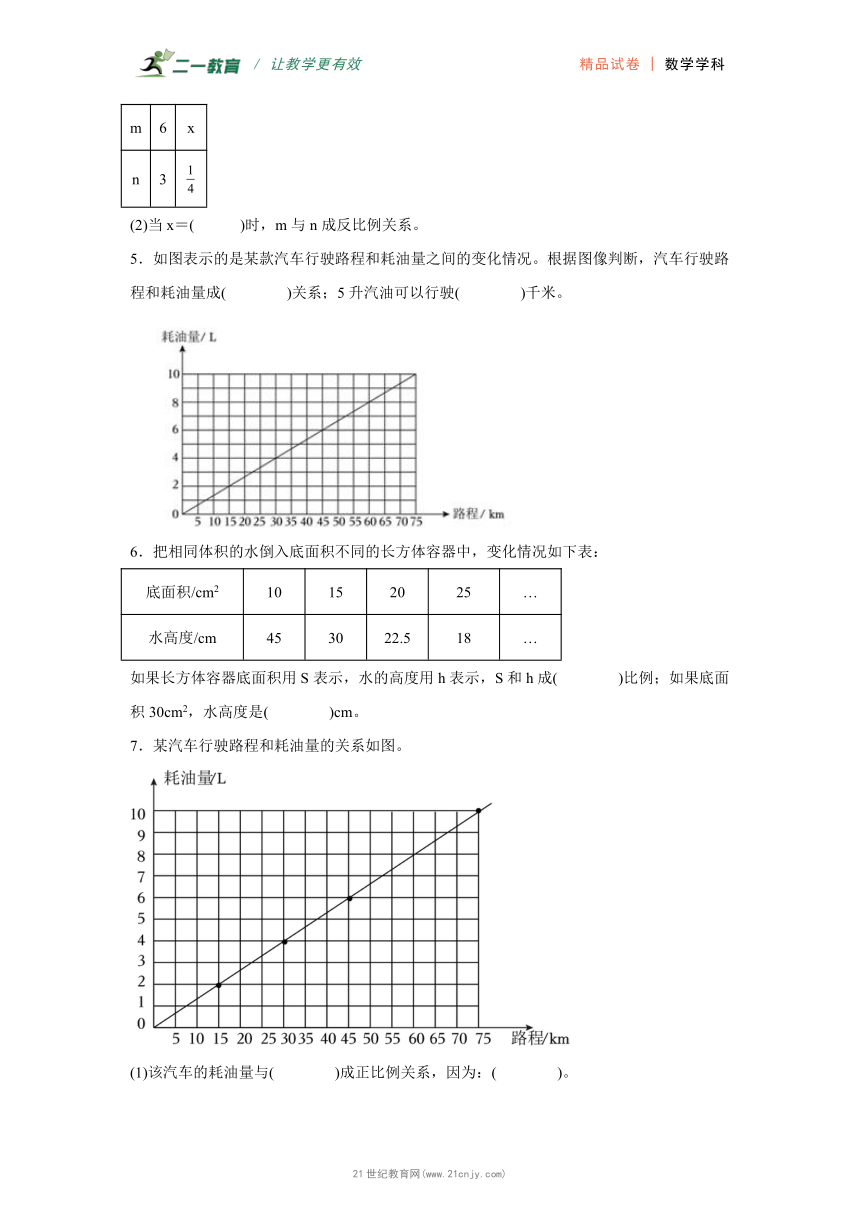
5.如图表示的是某款汽车行驶路程和耗油量之间的变化情况。根据图像判断,汽车行驶路程和耗油量成( )关系;5升汽油可以行驶( )千米。
6.把相同体积的水倒入底面积不同的长方体容器中,变化情况如下表:
底面积/cm2 10 15 20 25 …
水高度/cm 45 30 22.5 18 …
如果长方体容器底面积用S表示,水的高度用h表示,S和h成( )比例;如果底面积30cm2,水高度是( )cm。
7.某汽车行驶路程和耗油量的关系如图。
(1)该汽车的耗油量与( )成正比例关系,因为:( )。
(2)利用图像估计一下,该汽车行驶60千米的耗油量是( )。
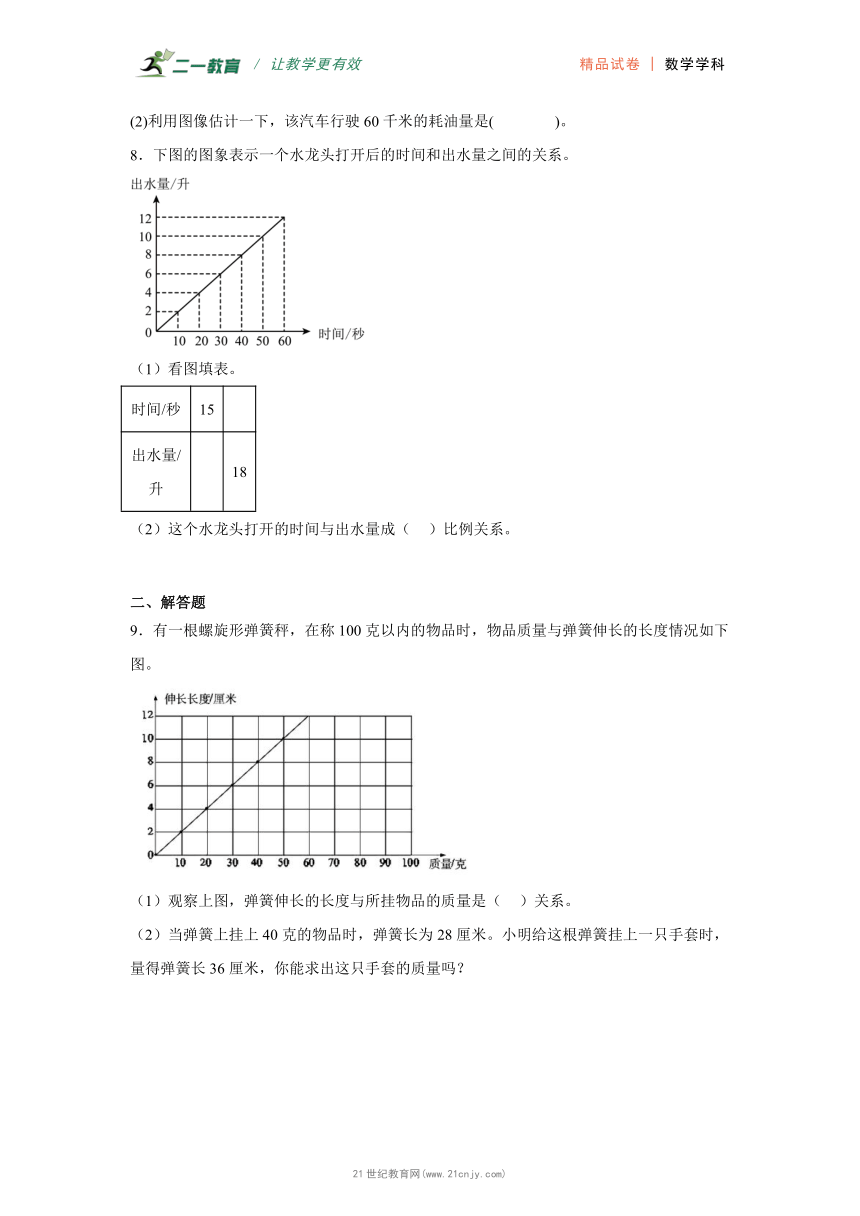
8.下图的图象表示一个水龙头打开后的时间和出水量之间的关系。
(1)看图填表。
时间/秒 15
出水量/升 18
(2)这个水龙头打开的时间与出水量成( )比例关系。
二、解答题
9.有一根螺旋形弹簧秤,在称100克以内的物品时,物品质量与弹簧伸长的长度情况如下图。
(1)观察上图,弹簧伸长的长度与所挂物品的质量是( )关系。
(2)当弹簧上挂上40克的物品时,弹簧长为28厘米。小明给这根弹簧挂上一只手套时,量得弹簧长36厘米,你能求出这只手套的质量吗?【版权所有:21教育】
10.下面图象表示淘气、笑笑骑车行驶的路程与时间的关系,看图回答问题。
(1)淘气骑车行驶的路程与时间成( )比例。(填“正”或“反”)
(2)从图象上看,( )骑车更快一些。(填“淘气”或“笑笑”)
(3)骑车2小时,笑笑行驶了多少千米?骑行40千米,淘气用了多长时间?
11.学校要给一间功能教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/平方米 0.2 0.3 0.4 0.6 0.8 …
所需地砖的数量/块 600 400 300 200 150 …
(1)每块地砖的面积和所需地砖的数量成( )比例关系。
(2)如果铺这一地面用了500块地砖,所用的地砖每块面积是多大?(用比例解答)
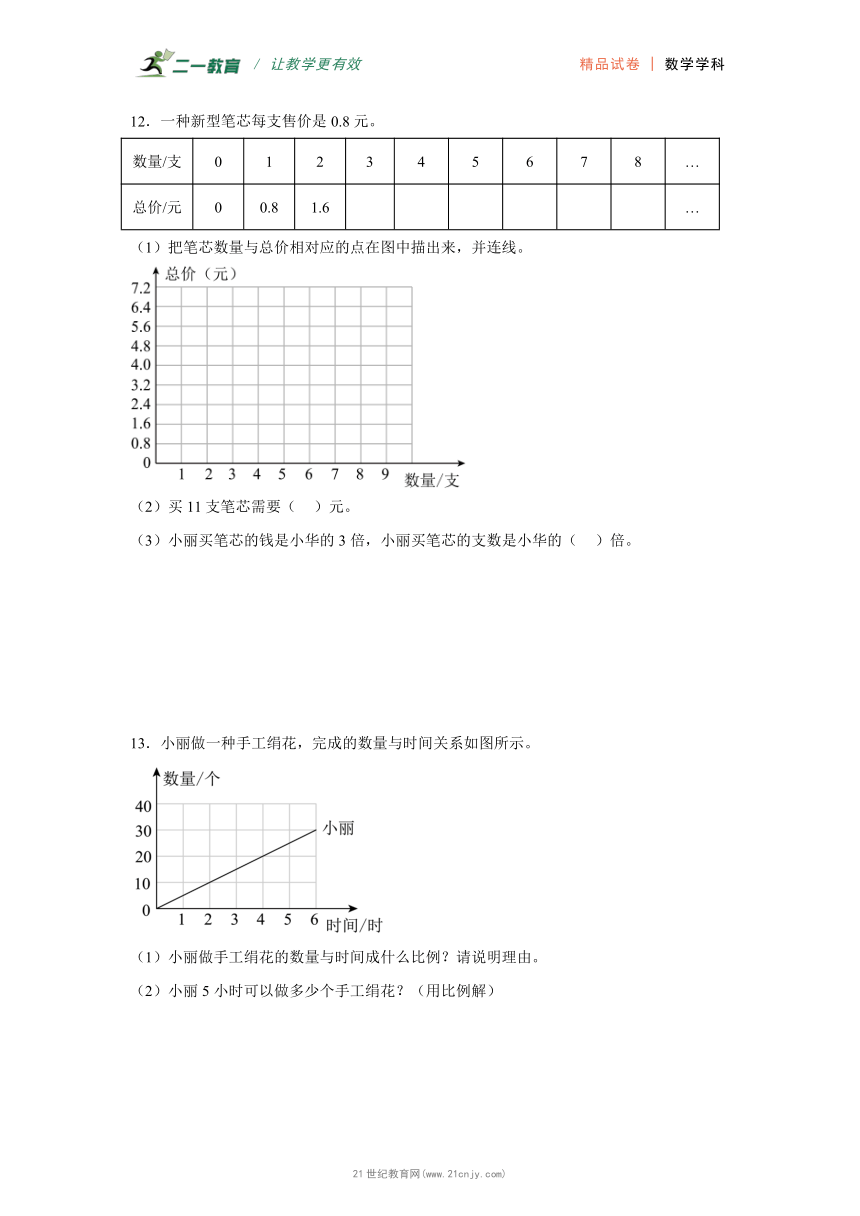
12.一种新型笔芯每支售价是0.8元。
数量/支 0 1 2 3 4 5 6 7 8 …
总价/元 0 0.8 1.6 …
(1)把笔芯数量与总价相对应的点在图中描出来,并连线。
(2)买11支笔芯需要( )元。
(3)小丽买笔芯的钱是小华的3倍,小丽买笔芯的支数是小华的( )倍。
13.小丽做一种手工绢花,完成的数量与时间关系如图所示。
(1)小丽做手工绢花的数量与时间成什么比例?请说明理由。
(2)小丽5小时可以做多少个手工绢花?(用比例解)
14.某牛奶公司把一批牛奶进行灌装,如表给出了几种不同的灌装方案。
方案 一 二 三
每瓶容量/升 0.25 0.2 0.5
瓶数 800 1000 400
(1)这批牛奶的总量是( )升。
(2)( )没有变化,每瓶容量和灌装的瓶数成( )比例。
(3)如果将这批牛奶装入250个瓶子里,每瓶要装多少升?(用比例解)
15.运20“鲲鹏”大型运输机是我国自主研制的第一款大型涡扇发动机运输机,可在复杂天气情况下执行多种运输任务,表重工是某架运20飞机的运输时间和飞行距离情况。
时间(小时) 1 2 3 4 ( )
距离(千米) 800 1600 ( ) 3200 4000
(1)把表格内容填完整。
(2)把表中的数据在图中方格纸上画图表示出来。
(3)照这样的速度,飞机3.5小时飞行( )千米;看图估计,飞机飞行4400千米,需要( )小时。21教育网
16.我们做过滴水实验,一个没有拧紧的水龙头的漏水情况如图。
(1)点A表示什么意思?
(2)如果用t表示时间,v表示漏水量,用式子表示它们的关系是,t和v是否成正比例?
(3)假设1个人每天喝水2升,一个月(30天计算)的漏水量可供这个人喝几天?
17.如图A(8,4)、B(20,10)是直线l上的两个点。(单位:厘米)
(1)如果C点(,45)也在l这条直线上,则=( )。
(2)直线l上的点P(,),和成( )比例。
(3)用点A、B和D(z,4)构成一个等腰三角形(z是一个整数),这个三角形绕它的对称轴旋转一周得到一个立体图形,这个立体图形的体积是多少?21·cn·jy·com
《第四单元专项练习05:正比例和反比例的意义与图像应用-2024-2025学年六年级数学下册典型》参考答案
1. 正 7.5
【分析】横轴代表时间,纵轴代表修路长度,如果修路长度与所用时间的比值一定,它们成正比例关系;如果修路长度与所用时间的乘积一定,它们成反比例关系,据此解答即可。
【详解】100÷1=100(米/天)
200÷2=100(米/天)
300÷3=100(米/天)
400÷4=100(米/天)
500÷5=100(米/天)
……
所以修路长度与所用时间的比值一定,它们成正比例关系。
修路的效率是平均每天修100米,则修长750米公路需要:750÷100=7.5(天)
2. 正 2
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
从图中选取几组数据,求路程与耗油量的比值,比值相等,则路程与耗油量成正比例。
从图中的横轴上找到20千米,再找到图象中的对应的点,然后找到纵轴上对应的耗油量即可。
【详解】===…==10(一定)
比值一定,则路程和耗油量成正比例。
汽车行驶的路程和耗油量成正比例,汽车行驶20千米,耗油2升。
3. 正 所挂物体的质量与弹簧伸长的长度的比值一定
【分析】当两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
【详解】1∶0.5=2∶1=3∶1.5=4∶2=5∶2.5=6∶3=10∶5=2
在弹簧的弹性限度内,所挂物体的质量与弹簧伸长的长度成正比例关系。理由如下:在弹簧的弹性限度内,发现物体质量增加,弹簧伸长长度也增加,且所挂物体的质量与弹簧伸长的长度的比值一定,因此在弹簧的弹性限度内,所挂物体的质量与弹簧伸长的长度成正比例。
4.(1)正
(2)72
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)当时,
,比值一定,m与n成正比例。
所以,当时,m与n成正比例。
(2)m与n成反比例,那么m与n的乘积一定,
解:
当x=72时,m与n成反比例关系。
5. 正 37.5
【分析】由于正比例的图像是一条直线,通过观察图像可知:汽车耗油量与所行路程成正比例关系;2升汽油可以行驶15千米,用2÷15即可求出每千米消耗的油量;进而求出5升汽油可以行驶的千米数。21·世纪*教育网
【详解】由于正比例的图像是一条直线,通过观察图像可知:汽车行驶路程和耗油量成正关系。
5÷(2÷15)
=5÷
=5×
=37.5(千米)
5升汽油可以行驶37.5千米。
6. 反 15
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量成反比例关系。www-2-1-cnjy-com
先从表格中任意选取一组数据,根据V=Sh求出水的体积,再根据h=V÷S,求出底面积是30cm2时水的高度。【来源:21cnj*y.co*m】
【详解】V=Sh,体积一定,即乘积一定,则底面积S与高h成反比例;
10×45÷30
=450÷30
=15(cm)
如果长方体容器底面积用S表示,水的高度用h表示,S和h成反比例;如果底面积30cm2,水高度是15cm。
7.(1) 路程 耗油量与路程是两个相关联的量且比值一定
(2)8升/8L
【分析】(1)判断两种量成正比例还是成反比例时,关键看这两种相关联的量中相对应的两个数是比值一定还是乘积一定。如果比值一定,就成正比例;如果乘积一定,就成反比例;如果比值和乘积都不是定量,就不成比例。
耗油量÷路程=每千米的耗油量(一定),所以该汽车的耗油量与路程成正比例关系;据此作答。
(2)根据统计图找出60千米对应的耗油量即可做出估计。
【详解】(1)该汽车的耗油量与路程成正比例关系,因为:耗油量与路程是两个相关联的量且比值一定。
(2)由图像可知,该汽车行驶60千米的耗油量是8升。
8.(1)3;90;(从左往右)
(2)正
【分析】(1)观察图象可知,横轴表示时间,纵轴表示出水量,单位长度表示2升,每秒的出水量=出水量÷时间,据此求出这个水龙头每秒的出水量,再计算表格中15秒的出水量和出水18升需要的时间;www.21-cn-jy.com
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。如果用字母和表示两种相关联的量,用表示它们的比值(一定),正比例关系可以用表示,据此解答。
【详解】(1)2÷10=0.2(升)
15×0.2=3(升)
18÷0.2=90(秒)
时间/秒 15 90
出水量/升 3 18
(2)(一定)
所以,这个水龙头打开的时间与出水量成正比例关系。
9.(1)正比例
(2)80克
【分析】(1)两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系,正比例图像是一条经过原点的直线,据此分析。
(2)弹簧长度-物品质量÷弹簧伸长1厘米对应的质量=弹簧原长,(弹簧长度-弹簧原长)×弹簧伸长1厘米对应的质量=称出的物品质量,据此列式解答。【出处:21教育名师】
【详解】(1)10÷2=5(克)、20÷4=5(克)、30÷6=5(克)……
弹簧伸长1厘米对应的质量是5克,图像是一条经过原点的直线,弹簧伸长的长度与所挂物品的质量是正比例关系。
(2)弹簧原长:
(厘米)
手套质量:(36-20)×5
=16×5
=80(克)
答:这只手套的质量是80克。
10.(1)正
(2)淘气
(3)20千米;时
【分析】(1)如果两个相关联量的比值一定,那么它们成正比例;如果两个相关联量的乘积一定,那么它们成反比例。据此解答;
(2)从图上看,淘气和笑笑都骑了50千米,淘气花的时间是3个多小时,笑笑花的时间是5个小时,同样的路程,花的时间少,速度就快,据此解答;
(3)图像的横轴表示时间,纵轴表示路程,从图像中找出笑笑2小时对应的路程,是20千米;从图像中可知,淘气骑行15千米花了1小时,先根据速度=路程÷时间,算出淘气的骑行速度,再根据时间=路程÷速度,算出淘气骑行40千米,所花的时间即可。
【详解】(1)15∶1=30∶2=45∶3=15
观察淘气的路程和时间数据,随着时间的增加,路程也在增加,并且路程与时间的比值是一定的,即速度一定,所以淘气骑车行驶的路程与时间成正比例。
(2)从图象上看,淘气骑车更快一些。
(3)由图可得,骑车2小时,笑笑行驶了20千米。
15÷1=15(千米/时)
40÷15=(时)
答:骑车2小时,笑笑行驶了20千米;骑行40千米,淘气用了时。
11.(1)反
(2)0.24平方米
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答即可。
(2)可假设所用的地砖每块面积是x平方米,根据每块地砖的面积和所需地砖的数量成反比例关系,据此即可列比例求解。
【详解】(1)0.2×600=0.3×400=0.4×300=0.6×200=0.8×150=120(平方米)
因为每块地砖的面积×需要的块数=铺地面积(一定),所以每块地砖的面积和所需地砖的数量成反比例关系。
(2)解:设所用地砖的面积为x平方米。
500x=0.2×600
500x=120
500x÷500=120÷500
x=0.24
答:所用的地砖每块面积是0.24平方米。
12.2.4;3.2;4.0;4.8;5.6;6.4
(1)图见详解
(2)8.8
(3)3
【分析】已知一种新型笔芯每支售价是0.8元,根据“单价×数量=总价”,求出买不同数量的笔芯对应的总价,据此把表格补充完整。
(1)把笔芯数量与总价相对应的点在图中描出来,并连线。
(2)根据“单价×数量=总价”,求出买11支笔芯需要的钱数。
(3)根据总价÷数量=单价,单价一定,则总价与数量成正比例关系,据此解答。
【详解】0.8×3=2.4(元)
0.8×4=3.2(元)
0.8×5=4.0(元)
0.8×6=4.8(元)
0.8×7=5.6(元)
0.8×8=6.4(元)
数量/支 0 1 2 3 4 5 6 7 8 …
总价/元 0 0.8 1.6 2.4 3.2 4.0 4.8 5.6 6.4 …
(1)如下图:
(2)0.8×11=8.8(元)
买11支笔芯需要8.8元。
(3)因为单价一定,总价与数量成正比例关系,所以小丽买笔芯的钱是小华的3倍,小丽买笔芯的支数是小华的3倍。21教育名师原创作品
13.(1)正比例;理由见详解
(2)25个
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。根据题意可知,每小时做绢花的数量不变,小丽做手工绢花的数量和时间成正比例;
(2)设小丽5小时可以做x个手工绢花,2小时做10个绢花,小丽做手工绢花的数量和时间成正比例,列比例:10∶2=x∶5,解比例,即可解答。
【详解】10÷2=20÷4=30÷6=5(一定)
答:小丽做手工绢花的数量与时间成正比例。做的数量和做的时间成正比例关系。
(2)解:设小丽5小时做x个手工绢花。
10∶2=x∶5
2x=10×5
2x=50
x=50÷2
x=25
答:小丽5小时可以做25个手工绢花。
14.(1)200
(2)这批牛奶的总量;反
(3)0.8升
【分析】(1)通过每瓶容量与瓶数的乘积可求出牛奶总量;
(2)判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。据此判断每瓶容量和灌装瓶数的关系;
(3)利用牛奶总量不变,每瓶容量和灌装瓶数成反比例这一性质列方程求解。
【详解】(1)0.25×800=200(升)
所以这批牛奶的总量是200升。
(2)这批牛奶的总量没有变,每瓶容量和灌装的瓶数成反比例。
(3)解:设每瓶要装x升。
250x=0.25×800
250x=200
250x÷250=200÷250
x=0.8
答:每瓶要装0.8升。
15.(1)见详解
(2)见详解
(3)2800;5.5
【分析】(1)根据题意可知,每小时飞行800千米,3小时飞行3个800千米,即800×3;4000千米里有几个800千米,分析4000千米需要几小时,即4000÷800;据此完成表格。
(2)根据表中的数据在图中方格纸上画图表示出来。
(3)用800×3.5,即可求出飞行3.5小时的路程;用4400÷800,飞机飞行4400千米,需要时间。21cnjy.com
【详解】(1)800×3=2400(千米)
4000÷800=5(小时)
如图:
时间(小时) 1 2 3 4 5
距离(千米) 800 1600 2400 3200 4000
(2)如图:
(3)800×3.5=2800(千米)
4400÷800=5.5(小时)
照这样的速度,飞机3.5小时飞行2800千米;看图估计,飞机飞行4400千米,需要5.5小时。
16.(1)水龙头6分钟漏水72毫升
(2)成正比例
(3)259.2天
【分析】(1)根据图形意义,列表示时间,行表示漏水量,据此解答;
(2)从图像上可以看出,水龙头每分钟漏水12毫升,根据漏水量÷时间=每分钟漏水量;写出关系式;再判断两种量是否成正比例;2·1·c·n·j·y
(3)先计算出水龙头一个月的漏水量,再求出可供几个人喝几天的,注意单位名数的换算。
【详解】(1)水龙头6分钟漏水72毫升。
(2)12∶1=24∶2=36∶3=48∶4=12
即v∶t=12(一定),t和v成正比例。
(3)12×60×24×30
=720×24×30
=172800×30
=518400(毫升)
518400毫升=518.4升
518.4÷2=259.2(天)
答:一个月的漏水量可供这个人喝259.2天。
17.(1)90
(2)正
(3)904.32立方厘米
【分析】(1)因为C点(,45)也在l这条直线上,可以与A点或B点组成比例方程,并求解,求出的值。21世纪教育网版权所有
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。【来源:21·世纪·教育·网】
(3)根据“等腰三角形的两条腰相等”以及点D的位置是(z,4),根据数对的知识可知,点D与点A在同一行,由此得出点D在图中的位置;2-1-c-n-j-y
因为这个三角形绕它的对称轴旋转一周得到一个立体图形,这个立体图形是圆锥;由点A、点B的数对,得出横轴、纵轴每格表示的长度,进而得出圆锥的底面半径和高,然后根据圆锥的体积公式V=πr2h,求出这个圆锥的体积。21*cnjy*com
【详解】(1)=
解:4=8×45
4=360
=360÷4
=90
如果C点(,45)也在l这条直线上,则=90。
(2)==…=2(一定)
那么直线l上的点P(,),=2,比值一定,和成正比例。
(3)如下图,点A、B和D(z,4)构成一个等腰三角形ABD。
横轴的每格表示:
(20-8)÷4
=12÷4
=3(厘米)
纵轴的每格表示:
(10-4)÷2
=6÷2
=3(厘米)
圆锥的底面半径:3×4=12(厘米)
圆锥的高:3×2=6(厘米)
×3.14×122×6
=×3.14×144×6
=904.32(立方厘米)
答:这个立体图形的体积是904.32立方厘米。
【点睛】(1)列出比例方程,并解比例。
(2)本题考查正比例的意义及辨识方法,也可以通过图象判断两种量是否成正比例。
(3)先根据等腰三角形的特征以及数对的知识找到D点的位置,再判断旋转而成的立体图形是圆锥,确定圆锥的底面半径和高,根据圆锥的体积公式解答。21*cnjy*com
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第四单元专项练习05:正比例和反比例的意义与图像应用
1.如下图表示一工程队修筑公路的长度与所用时间的关系,这个工程队修路长度与所用时间成( )比例,照这样计算,修长750米公路需要( )天。
2.下图表示一辆汽车行驶的路程和耗油量之间的关系。汽车行驶的路程和耗油量成( )比例,汽车行驶20千米,耗油( )升。
3.科学小组的同学做实验,在弹簧的弹性限度内,所挂物体的质量与弹簧伸长的长度情况如下表:
物体质量(kg) 0 1 2 3 4 5 6 … 10
弹簧伸长长度(cm) 0 0.5 1 1.5 2 2.5 3 5
根据科学小组测量的数据,在弹簧的弹性限度内,所挂物体的质量与弹簧伸长的长度成( )比例关系,在下面简要说明理由:( )。
4.如表中m和n是两个相关联的量。
(1)当时,m与n成( )比例关系。
m 6 x
n 3
(2)当x=( )时,m与n成反比例关系。
5.如图表示的是某款汽车行驶路程和耗油量之间的变化情况。根据图像判断,汽车行驶路程和耗油量成( )关系;5升汽油可以行驶( )千米。
6.把相同体积的水倒入底面积不同的长方体容器中,变化情况如下表:
底面积/cm2 10 15 20 25 …
水高度/cm 45 30 22.5 18 …
如果长方体容器底面积用S表示,水的高度用h表示,S和h成( )比例;如果底面积30cm2,水高度是( )cm。
7.某汽车行驶路程和耗油量的关系如图。
(1)该汽车的耗油量与( )成正比例关系,因为:( )。
(2)利用图像估计一下,该汽车行驶60千米的耗油量是( )。
8.下图的图象表示一个水龙头打开后的时间和出水量之间的关系。
(1)看图填表。
时间/秒 15
出水量/升 18
(2)这个水龙头打开的时间与出水量成( )比例关系。
二、解答题
9.有一根螺旋形弹簧秤,在称100克以内的物品时,物品质量与弹簧伸长的长度情况如下图。
(1)观察上图,弹簧伸长的长度与所挂物品的质量是( )关系。
(2)当弹簧上挂上40克的物品时,弹簧长为28厘米。小明给这根弹簧挂上一只手套时,量得弹簧长36厘米,你能求出这只手套的质量吗?【版权所有:21教育】
10.下面图象表示淘气、笑笑骑车行驶的路程与时间的关系,看图回答问题。
(1)淘气骑车行驶的路程与时间成( )比例。(填“正”或“反”)
(2)从图象上看,( )骑车更快一些。(填“淘气”或“笑笑”)
(3)骑车2小时,笑笑行驶了多少千米?骑行40千米,淘气用了多长时间?
11.学校要给一间功能教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/平方米 0.2 0.3 0.4 0.6 0.8 …
所需地砖的数量/块 600 400 300 200 150 …
(1)每块地砖的面积和所需地砖的数量成( )比例关系。
(2)如果铺这一地面用了500块地砖,所用的地砖每块面积是多大?(用比例解答)
12.一种新型笔芯每支售价是0.8元。
数量/支 0 1 2 3 4 5 6 7 8 …
总价/元 0 0.8 1.6 …
(1)把笔芯数量与总价相对应的点在图中描出来,并连线。
(2)买11支笔芯需要( )元。
(3)小丽买笔芯的钱是小华的3倍,小丽买笔芯的支数是小华的( )倍。
13.小丽做一种手工绢花,完成的数量与时间关系如图所示。
(1)小丽做手工绢花的数量与时间成什么比例?请说明理由。
(2)小丽5小时可以做多少个手工绢花?(用比例解)
14.某牛奶公司把一批牛奶进行灌装,如表给出了几种不同的灌装方案。
方案 一 二 三
每瓶容量/升 0.25 0.2 0.5
瓶数 800 1000 400
(1)这批牛奶的总量是( )升。
(2)( )没有变化,每瓶容量和灌装的瓶数成( )比例。
(3)如果将这批牛奶装入250个瓶子里,每瓶要装多少升?(用比例解)
15.运20“鲲鹏”大型运输机是我国自主研制的第一款大型涡扇发动机运输机,可在复杂天气情况下执行多种运输任务,表重工是某架运20飞机的运输时间和飞行距离情况。
时间(小时) 1 2 3 4 ( )
距离(千米) 800 1600 ( ) 3200 4000
(1)把表格内容填完整。
(2)把表中的数据在图中方格纸上画图表示出来。
(3)照这样的速度,飞机3.5小时飞行( )千米;看图估计,飞机飞行4400千米,需要( )小时。21教育网
16.我们做过滴水实验,一个没有拧紧的水龙头的漏水情况如图。
(1)点A表示什么意思?
(2)如果用t表示时间,v表示漏水量,用式子表示它们的关系是,t和v是否成正比例?
(3)假设1个人每天喝水2升,一个月(30天计算)的漏水量可供这个人喝几天?
17.如图A(8,4)、B(20,10)是直线l上的两个点。(单位:厘米)
(1)如果C点(,45)也在l这条直线上,则=( )。
(2)直线l上的点P(,),和成( )比例。
(3)用点A、B和D(z,4)构成一个等腰三角形(z是一个整数),这个三角形绕它的对称轴旋转一周得到一个立体图形,这个立体图形的体积是多少?21·cn·jy·com
《第四单元专项练习05:正比例和反比例的意义与图像应用-2024-2025学年六年级数学下册典型》参考答案
1. 正 7.5
【分析】横轴代表时间,纵轴代表修路长度,如果修路长度与所用时间的比值一定,它们成正比例关系;如果修路长度与所用时间的乘积一定,它们成反比例关系,据此解答即可。
【详解】100÷1=100(米/天)
200÷2=100(米/天)
300÷3=100(米/天)
400÷4=100(米/天)
500÷5=100(米/天)
……
所以修路长度与所用时间的比值一定,它们成正比例关系。
修路的效率是平均每天修100米,则修长750米公路需要:750÷100=7.5(天)
2. 正 2
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
从图中选取几组数据,求路程与耗油量的比值,比值相等,则路程与耗油量成正比例。
从图中的横轴上找到20千米,再找到图象中的对应的点,然后找到纵轴上对应的耗油量即可。
【详解】===…==10(一定)
比值一定,则路程和耗油量成正比例。
汽车行驶的路程和耗油量成正比例,汽车行驶20千米,耗油2升。
3. 正 所挂物体的质量与弹簧伸长的长度的比值一定
【分析】当两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
【详解】1∶0.5=2∶1=3∶1.5=4∶2=5∶2.5=6∶3=10∶5=2
在弹簧的弹性限度内,所挂物体的质量与弹簧伸长的长度成正比例关系。理由如下:在弹簧的弹性限度内,发现物体质量增加,弹簧伸长长度也增加,且所挂物体的质量与弹簧伸长的长度的比值一定,因此在弹簧的弹性限度内,所挂物体的质量与弹簧伸长的长度成正比例。
4.(1)正
(2)72
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)当时,
,比值一定,m与n成正比例。
所以,当时,m与n成正比例。
(2)m与n成反比例,那么m与n的乘积一定,
解:
当x=72时,m与n成反比例关系。
5. 正 37.5
【分析】由于正比例的图像是一条直线,通过观察图像可知:汽车耗油量与所行路程成正比例关系;2升汽油可以行驶15千米,用2÷15即可求出每千米消耗的油量;进而求出5升汽油可以行驶的千米数。21·世纪*教育网
【详解】由于正比例的图像是一条直线,通过观察图像可知:汽车行驶路程和耗油量成正关系。
5÷(2÷15)
=5÷
=5×
=37.5(千米)
5升汽油可以行驶37.5千米。
6. 反 15
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量成反比例关系。www-2-1-cnjy-com
先从表格中任意选取一组数据,根据V=Sh求出水的体积,再根据h=V÷S,求出底面积是30cm2时水的高度。【来源:21cnj*y.co*m】
【详解】V=Sh,体积一定,即乘积一定,则底面积S与高h成反比例;
10×45÷30
=450÷30
=15(cm)
如果长方体容器底面积用S表示,水的高度用h表示,S和h成反比例;如果底面积30cm2,水高度是15cm。
7.(1) 路程 耗油量与路程是两个相关联的量且比值一定
(2)8升/8L
【分析】(1)判断两种量成正比例还是成反比例时,关键看这两种相关联的量中相对应的两个数是比值一定还是乘积一定。如果比值一定,就成正比例;如果乘积一定,就成反比例;如果比值和乘积都不是定量,就不成比例。
耗油量÷路程=每千米的耗油量(一定),所以该汽车的耗油量与路程成正比例关系;据此作答。
(2)根据统计图找出60千米对应的耗油量即可做出估计。
【详解】(1)该汽车的耗油量与路程成正比例关系,因为:耗油量与路程是两个相关联的量且比值一定。
(2)由图像可知,该汽车行驶60千米的耗油量是8升。
8.(1)3;90;(从左往右)
(2)正
【分析】(1)观察图象可知,横轴表示时间,纵轴表示出水量,单位长度表示2升,每秒的出水量=出水量÷时间,据此求出这个水龙头每秒的出水量,再计算表格中15秒的出水量和出水18升需要的时间;www.21-cn-jy.com
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。如果用字母和表示两种相关联的量,用表示它们的比值(一定),正比例关系可以用表示,据此解答。
【详解】(1)2÷10=0.2(升)
15×0.2=3(升)
18÷0.2=90(秒)
时间/秒 15 90
出水量/升 3 18
(2)(一定)
所以,这个水龙头打开的时间与出水量成正比例关系。
9.(1)正比例
(2)80克
【分析】(1)两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系,正比例图像是一条经过原点的直线,据此分析。
(2)弹簧长度-物品质量÷弹簧伸长1厘米对应的质量=弹簧原长,(弹簧长度-弹簧原长)×弹簧伸长1厘米对应的质量=称出的物品质量,据此列式解答。【出处:21教育名师】
【详解】(1)10÷2=5(克)、20÷4=5(克)、30÷6=5(克)……
弹簧伸长1厘米对应的质量是5克,图像是一条经过原点的直线,弹簧伸长的长度与所挂物品的质量是正比例关系。
(2)弹簧原长:
(厘米)
手套质量:(36-20)×5
=16×5
=80(克)
答:这只手套的质量是80克。
10.(1)正
(2)淘气
(3)20千米;时
【分析】(1)如果两个相关联量的比值一定,那么它们成正比例;如果两个相关联量的乘积一定,那么它们成反比例。据此解答;
(2)从图上看,淘气和笑笑都骑了50千米,淘气花的时间是3个多小时,笑笑花的时间是5个小时,同样的路程,花的时间少,速度就快,据此解答;
(3)图像的横轴表示时间,纵轴表示路程,从图像中找出笑笑2小时对应的路程,是20千米;从图像中可知,淘气骑行15千米花了1小时,先根据速度=路程÷时间,算出淘气的骑行速度,再根据时间=路程÷速度,算出淘气骑行40千米,所花的时间即可。
【详解】(1)15∶1=30∶2=45∶3=15
观察淘气的路程和时间数据,随着时间的增加,路程也在增加,并且路程与时间的比值是一定的,即速度一定,所以淘气骑车行驶的路程与时间成正比例。
(2)从图象上看,淘气骑车更快一些。
(3)由图可得,骑车2小时,笑笑行驶了20千米。
15÷1=15(千米/时)
40÷15=(时)
答:骑车2小时,笑笑行驶了20千米;骑行40千米,淘气用了时。
11.(1)反
(2)0.24平方米
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答即可。
(2)可假设所用的地砖每块面积是x平方米,根据每块地砖的面积和所需地砖的数量成反比例关系,据此即可列比例求解。
【详解】(1)0.2×600=0.3×400=0.4×300=0.6×200=0.8×150=120(平方米)
因为每块地砖的面积×需要的块数=铺地面积(一定),所以每块地砖的面积和所需地砖的数量成反比例关系。
(2)解:设所用地砖的面积为x平方米。
500x=0.2×600
500x=120
500x÷500=120÷500
x=0.24
答:所用的地砖每块面积是0.24平方米。
12.2.4;3.2;4.0;4.8;5.6;6.4
(1)图见详解
(2)8.8
(3)3
【分析】已知一种新型笔芯每支售价是0.8元,根据“单价×数量=总价”,求出买不同数量的笔芯对应的总价,据此把表格补充完整。
(1)把笔芯数量与总价相对应的点在图中描出来,并连线。
(2)根据“单价×数量=总价”,求出买11支笔芯需要的钱数。
(3)根据总价÷数量=单价,单价一定,则总价与数量成正比例关系,据此解答。
【详解】0.8×3=2.4(元)
0.8×4=3.2(元)
0.8×5=4.0(元)
0.8×6=4.8(元)
0.8×7=5.6(元)
0.8×8=6.4(元)
数量/支 0 1 2 3 4 5 6 7 8 …
总价/元 0 0.8 1.6 2.4 3.2 4.0 4.8 5.6 6.4 …
(1)如下图:
(2)0.8×11=8.8(元)
买11支笔芯需要8.8元。
(3)因为单价一定,总价与数量成正比例关系,所以小丽买笔芯的钱是小华的3倍,小丽买笔芯的支数是小华的3倍。21教育名师原创作品
13.(1)正比例;理由见详解
(2)25个
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。根据题意可知,每小时做绢花的数量不变,小丽做手工绢花的数量和时间成正比例;
(2)设小丽5小时可以做x个手工绢花,2小时做10个绢花,小丽做手工绢花的数量和时间成正比例,列比例:10∶2=x∶5,解比例,即可解答。
【详解】10÷2=20÷4=30÷6=5(一定)
答:小丽做手工绢花的数量与时间成正比例。做的数量和做的时间成正比例关系。
(2)解:设小丽5小时做x个手工绢花。
10∶2=x∶5
2x=10×5
2x=50
x=50÷2
x=25
答:小丽5小时可以做25个手工绢花。
14.(1)200
(2)这批牛奶的总量;反
(3)0.8升
【分析】(1)通过每瓶容量与瓶数的乘积可求出牛奶总量;
(2)判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。据此判断每瓶容量和灌装瓶数的关系;
(3)利用牛奶总量不变,每瓶容量和灌装瓶数成反比例这一性质列方程求解。
【详解】(1)0.25×800=200(升)
所以这批牛奶的总量是200升。
(2)这批牛奶的总量没有变,每瓶容量和灌装的瓶数成反比例。
(3)解:设每瓶要装x升。
250x=0.25×800
250x=200
250x÷250=200÷250
x=0.8
答:每瓶要装0.8升。
15.(1)见详解
(2)见详解
(3)2800;5.5
【分析】(1)根据题意可知,每小时飞行800千米,3小时飞行3个800千米,即800×3;4000千米里有几个800千米,分析4000千米需要几小时,即4000÷800;据此完成表格。
(2)根据表中的数据在图中方格纸上画图表示出来。
(3)用800×3.5,即可求出飞行3.5小时的路程;用4400÷800,飞机飞行4400千米,需要时间。21cnjy.com
【详解】(1)800×3=2400(千米)
4000÷800=5(小时)
如图:
时间(小时) 1 2 3 4 5
距离(千米) 800 1600 2400 3200 4000
(2)如图:
(3)800×3.5=2800(千米)
4400÷800=5.5(小时)
照这样的速度,飞机3.5小时飞行2800千米;看图估计,飞机飞行4400千米,需要5.5小时。
16.(1)水龙头6分钟漏水72毫升
(2)成正比例
(3)259.2天
【分析】(1)根据图形意义,列表示时间,行表示漏水量,据此解答;
(2)从图像上可以看出,水龙头每分钟漏水12毫升,根据漏水量÷时间=每分钟漏水量;写出关系式;再判断两种量是否成正比例;2·1·c·n·j·y
(3)先计算出水龙头一个月的漏水量,再求出可供几个人喝几天的,注意单位名数的换算。
【详解】(1)水龙头6分钟漏水72毫升。
(2)12∶1=24∶2=36∶3=48∶4=12
即v∶t=12(一定),t和v成正比例。
(3)12×60×24×30
=720×24×30
=172800×30
=518400(毫升)
518400毫升=518.4升
518.4÷2=259.2(天)
答:一个月的漏水量可供这个人喝259.2天。
17.(1)90
(2)正
(3)904.32立方厘米
【分析】(1)因为C点(,45)也在l这条直线上,可以与A点或B点组成比例方程,并求解,求出的值。21世纪教育网版权所有
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。【来源:21·世纪·教育·网】
(3)根据“等腰三角形的两条腰相等”以及点D的位置是(z,4),根据数对的知识可知,点D与点A在同一行,由此得出点D在图中的位置;2-1-c-n-j-y
因为这个三角形绕它的对称轴旋转一周得到一个立体图形,这个立体图形是圆锥;由点A、点B的数对,得出横轴、纵轴每格表示的长度,进而得出圆锥的底面半径和高,然后根据圆锥的体积公式V=πr2h,求出这个圆锥的体积。21*cnjy*com
【详解】(1)=
解:4=8×45
4=360
=360÷4
=90
如果C点(,45)也在l这条直线上,则=90。
(2)==…=2(一定)
那么直线l上的点P(,),=2,比值一定,和成正比例。
(3)如下图,点A、B和D(z,4)构成一个等腰三角形ABD。
横轴的每格表示:
(20-8)÷4
=12÷4
=3(厘米)
纵轴的每格表示:
(10-4)÷2
=6÷2
=3(厘米)
圆锥的底面半径:3×4=12(厘米)
圆锥的高:3×2=6(厘米)
×3.14×122×6
=×3.14×144×6
=904.32(立方厘米)
答:这个立体图形的体积是904.32立方厘米。
【点睛】(1)列出比例方程,并解比例。
(2)本题考查正比例的意义及辨识方法,也可以通过图象判断两种量是否成正比例。
(3)先根据等腰三角形的特征以及数对的知识找到D点的位置,再判断旋转而成的立体图形是圆锥,确定圆锥的底面半径和高,根据圆锥的体积公式解答。21*cnjy*com
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
