期中真题专项复习12 证明题(含解析)--2024-2025学年浙教版七年级数学下册(浙江专用)
文档属性
| 名称 | 期中真题专项复习12 证明题(含解析)--2024-2025学年浙教版七年级数学下册(浙江专用) |

|
|
| 格式 | docx | ||
| 文件大小 | 605.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览




文档简介
2024-2025学年浙教版七年级数学下册(浙江专用)
期中真题专项复习12 证明题
一、证明题
1.(2024七下·温州期中)如图,已知,,,则.完成下面的说理过程.
解:(已知)
______(______)
(已知)
(等量代换)
______(______)
______(______)
(已知)
______(等量代换)
(______).
2.(2024七下·杭州期中)如图,已知 ,请你再画一个 ,使,,且交 边与点P.
(1)探究: 与有怎样的数量关系? 并说明理由.
(2)在(1)的条件下,若,求x、 y的值.
3.(2024七下·诸暨期中)如图,已知,,垂足分别为,F,,试说明.
将下面的解答过程补充完整.
证明:,(已知)
又
.
4.(2024七下·开化期中)如图,若,BD平分,则.完成下面的说理过程:
解:∵,
根据( )
得: .
再根据“两直线平行,内错角相等”,
得 .
∵BD平分,
∴ .
∴.
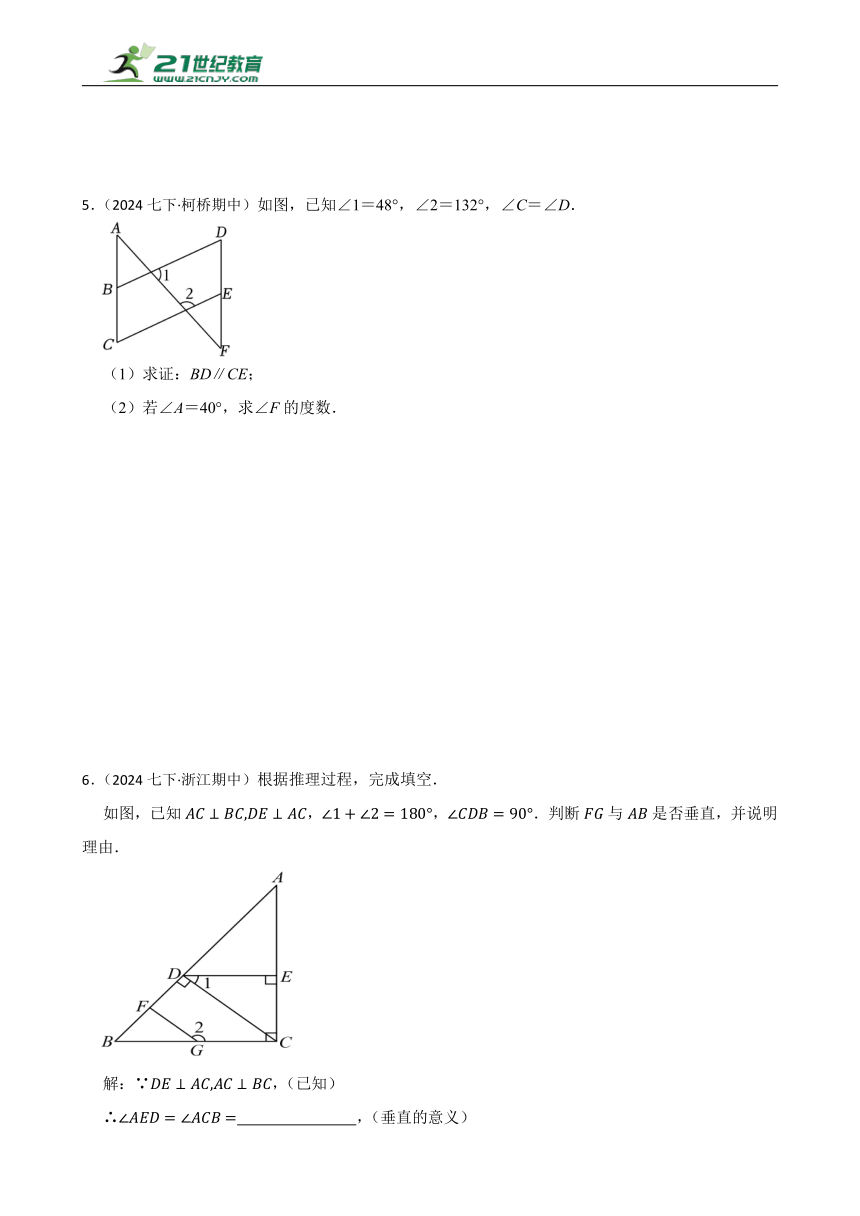
5.(2024七下·柯桥期中)如图,已知∠1=48°,∠2=132°,∠C=∠D.
(1)求证:BD∥CE;
(2)若∠A=40°,求∠F的度数.
6.(2024七下·浙江期中)根据推理过程,完成填空.
如图,已知,,.判断与是否垂直,并说明理由.
解:∵,(已知)
∴ ,(垂直的意义)
∴ .( )
∴,( )
又∵,(已知)
∴ .( )
∴.( )
∴ .(两直线平行,同位角相等)
7.(2024七下·修水期中) 如图,已知,.
(1)与平行吗?请说明理由.
(2)与的位置关系如何?为什么?
8.(2024七下·慈溪期中)如图,在四边形中,,.
(1)求的度数;
(2)若平分交于点,,求证:.
9.(2024七下·慈溪期中)如图,在中,平分,过点作交于点,过点作交于点,则可推得平分,其推导过程和推理依据如下:
解:,(已知)
▲ ( ▲ )
,(已知)
∴ ▲ =,( ▲ )
▲ .( ▲ )
.(等量代换)
又∵平分,(已知)
.( ▲ )
▲ .(等量代换)
∴平分.(角平分线定义)
请完善以上推导过程和推理依据,并按照顺序将相应内容填写在答题卡指定区域内.
10.(2024七下·义乌期中)如图,D是BC上一点,DE∥AB,交AC于点E,F是AB上一点,且∠DEC+∠AFD=180°.
(1)求证:DF∥AC;
(2)若∠B+∠C=130°,求∠FDE的度数.
11.(2024七下·拱墅期中)如图,已知,.
(1)与是否平行?请说明理由.
(2)与是否相等?请说明理由.
12.(2024七下·嘉善期中)如图,D,E分别在的边、上,F在线段上,且,.求证:.
13.(2024七下·拱墅期中)如图,在三角形中,D,E,F分别是上的点,且.
(1)若,试判断与是否垂直,并说明理由;
(2)若平分,,求的度数.
14.(2024七下·西湖期中)已知:点E在线段间(如图1).连接..
(1)求证:.
(2)如图2,点F在点E右侧.连接.
求证.
(3)如图3在(2)的条件下,线段,的延长线交于点H.交于点K.当平分,平分,,时,求的度数.
15.(2024七下·新昌期中)已知:如图,,,则.完成下面的说理过程(填空)
解:∵,(已知)
∴______(____________).
∵(____________),
∴______=______(等量代换).
∴(____________).
16.(2024七下·新昌期中)已知:如图,AB∥CD,∠A=∠D
则AF∥ED.完成下面的说理过程(填空)
解:∵AB∥CD,(已知)
∴∠A= ▲ .( )
∵∠A=∠D,( )
∴ ▲ = ▲ .(等式性质)
∴AF∥ED.( )
17.(2024七下·杭州期中)如图,∠AEF=80°,且∠A=x°,∠C=y°,∠F=z°.若+|y-80-m|+|z-40|=0(m为常数,且0<m<100)
(1) 求∠A、∠C的度数(用含m的代数式表示)
(2) 求证:AB∥CD
(3) 若∠A=40°,∠BAM=20°,∠EFM=10°,直线AM与直线FM交于点M,直接写出∠AMF的度数
18.(2024七下·温州期中) 如图,与相交于点F,,.
(1)试判断与的位置关系,并说明理由.
(2)若平分,,求的度数.
19.(2024七下·临海期中) 如图,已知,,垂足分别为D、F,,试说明:.请补充说明过程,并在括号内填上相应的理由.
解:,(已知),
(_▲_),
(_▲_).
_▲__(_▲_)
(已知).
(_▲_).
∴_▲_(_▲_)
(_▲_).
20.(2024七下·慈溪期中)如图,在四边形中,,.
(1)求的度数;
(2)若平分交于点,,求证:.
21.(2024七下·余杭期中)如图,已知BC∥DF,∠B=∠D,A、F、B三点共线,连接AC交DF于点E.
(1)求证:∠A=∠ACD.
(2)若FG∥AC,∠A+∠B=108°,求∠EFG的度数.
22.(2024七下·苍南期中)完成下面的证明过程.
如图,点D,G分别在三角形的边,上,于点E,于点F,连结.若,试说明的理由.
解:,
.
( ).
( ).
( ).
23.(2024七下·镇海区期中)如图,已知F,E分别是射线上的点.连接,其中平分,平分,.
(1)试说明;
(2)若,求的度数.
24.(2024七下·温州期中)如图,已知,则.完成下面的说理过程.
解:(已知)
▲ )
(已知)
(等量代换)
∴ ▲ //AB( )
▲
(已知)
▲ (等量代换)( )
∴DE∥AC( )
25.(2024七下·奉化期中)如图,AC∥EF,∠1+∠3=180°.
(1)判断AF与DC平行吗?请说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=80°,求∠BCD的度数.
26.(2024七下·义乌期中)如图,D是上一点,,交于点E,F是上一点,且.
(1)求证:;
(2)若,求的度数.
27.(2024七下·鄞州期中)如图,在三角形中,点D在上,交于点E,点F在,.
(1)试说明:;
(2)若,求的度数.
28.(2024七下·义乌期中)综合与实践数学社团的同学以“两条平行线,和一块含角的直角三角板”为主题开展数学活动,已知点E,F不能同时落在直线和之间.
(1)观察猜想:如图1,把三角板的角的顶点E,G分别放在,上,若,则的度数为______;(直接写出结论,不说明理由)
(2)类比探究:如图2,把三角板的锐角顶点G放在上,且保持不动,绕点G转动三角板,若点E恰好落在和之间,且与所夹锐角为,求的度数;
(3)解决问题:把三角板的锐角顶点放在上,在绕点旋转三角板的过程中,若存在,请直接写出射线与相交所夹锐角的度数.
29.(2024七下·镇海区期中)已知:如图,,判断.
下面是嘉琪同学的解题过程,请在括号中注明依据,在横线上补全步骤.
解:∵( ),
( ),
(等量代换).
又∵(已知),
∴ ,
∴( ).
30.(2024七下·路桥期中)如图,已知.求证:平分.
证明:( ),
▲ ( ),
▲ ( ),
(已知),
▲ = ▲ (等量代换).
平分( ),
答案解析部分
1.解:(已知)
(两直线平行,同旁内角互补)
(已知)
(等量代换)
(同旁内角互补,两直线平行)
(两直线平行,内错角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
根据题干信息提示,逐步完善推理过程与推理依据即可.
2.(1)解:与相等或互补,理由如下:
如图1,
,
,
,
,
,
如图2,
,
,
,
,
,
综上所述,与相等或互补;
(2)解:与相等或互补,
或,
,
或,
解得:或,
,或,.
(1)先分两种情况画图,利用平行线的性质解答即可;
(2)根据题(1)的结论列方程,再结合,解方程组求出x,y的值即可.
3.垂直定义;同位角相等,两直线平行;;已知;;;等量代换
4.两同旁内角互补,两直线平行;AB;CD;∠D;
解:∵,
根据两同旁内角互补,两直线平行,
得AB∥CD,
再根据“两直线平行,内错角相等”,
得
∵BD平分,
∴,
∴.
故答案为:两同旁内角互补,两直线平行;AB;CD;∠D;.
根据平行线的判定和性质以及角平分线的定义即可求解.
5.(1)证明:∵∠1=48°,∠2=132°,
∴∠1+∠2=180°,
∴BD∥CE;
(2)解:∵BD∥CE,
∴∠C=∠ABD,
又∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F=40°
(1)由“同旁内角互补,两直线平行”即可得到结论;
(2)由平行线的性质可得∠C=∠ABD,再结合 ∠C=∠D ,利用平行线的判定定理可得AC//DF,再由平行线的性质即可得到结论.
6.;同位角相等,两直线平行;两直线平行,内错角相等;;等量代换;同旁内角互补,两直线平行;
7.(1)解:与平行.
理由如下:
因为,,
所以,
所以.
(2)解:与平行.
理由如下:
因为,
所以.
因为,
所以.
所以.
(1)由邻补角的定义和 可得,根据平行线的判定定理即可得到结论.
(2)根据平行线的性质和等量代换得,根据平行线的判定定理可得到结论.
8.(1)解:解:,
,
,
,
的度数是110°;
(2)证明:∵平分交于点,=110°,
,
,
,
,
,
.
(1)根据平行线的性质得,最后进行计算即可求出答案;
(2)根据角平分线的定义求出∠DAE=55°,再根据平行线的性质得∠AEB=∠DAE=55°,从而得∠AEB=∠BCD,最后根据平行线的判定得AE∥CD.
9.解:,(已知)
(两直线平行,内错角相等)
,(已知)
∴=,(两直线平行,内错角相等)
(两直线平行,同位角相等;)
.(等量代换)
又∵平分,(已知)
.(角平分线定义)
∠BEF.(等量代换)
∴平分.(角平分线定义)
根据平行线的性质以及角平分线的定义即可得到答案.
10.(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
根据(1)可知:,,
∵,
∴,
∵,
∴.
(1)根据平行线的性质得到,进而结合题意得到,再根据平行线的判定即可求解;
(2)先根据题意得到,进而根据(1)可知:,,从而根据平行线的性质即可求解。
11.(1)解:,理由如下:
∵,
,
∴.
(2)解:,理由如下:
∵,
,
,
,
,
.
(1)根据“同角的补角相等”可得,然后根据"同位角相等两直线平行"可求解;
(2)先根据平行线的性质“两直线平行,内错角相等”可得,结合已知可得,然后根据"同位角相等两直线平行"可得,再根据平行线的性质“两直线平行,同位角相等”即可求解.
12.证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴.
先证明,可得,于是根据平行线的性质可得,再根据平行线性质得,等量代换即可证明结论.
13.(1)解:,理由如下:
,
,
∴∠BFD=∠FDE.
,
,
,
.
(2)解:平分,
,
,
,∠AFE=∠FED.
∵△FDE中,∠FDE+∠DFE+∠FED=2∠FDE+∠AFE=180°,
又∵∠FDE+3∠AFE=180°,
∴2∠FDE+∠AFE=∠FDE+3∠AFE,即∠FDE=2∠AFE.
∴5∠AFE=180°,
解得:∠AFE=36°,
∴∠BFE=2∠FDE=4∠AFE=144°.
14.(1)解:如图,过点E作,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:如图,过点F作,
∵,
∴,
∴,
∴,
即;
(3)解:设,∵平分,平分,
∴,
∴,
由(1)得:,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
解得:,
∴,
∴.
15.;两直线平行,内错角相等;已知;;;同位角相等,两直线平行
16.解:∵AB∥CD,(已知)
∴∠A=.(两直线平行,内错角相等)
∵∠A=∠D,(已知)
∴.(等式性质)
∴AF∥ED.(同位角相等,两直线平行)
由平行线的性质可得内错角相等,结合条件中的角度关系得到新的平行线.
17.(1) ∵+|y-80-m|+|z-40|=0(m为常数,且0<m<100),∴x-m-20=0,y-80-m=0,z-40=0,
∴∠A=x°=m+20°,∠C=y°=m+80°,z=40°,
(2) 过点F作FG∥AB,过点E作EH∥AB,
∴EH∥FG,
∴∠BAE=∠AEH=m+20°,∠EFG=∠FEH,
∴∠EFG=∠AEF-∠AEH=80°-(m+20°)=60°-m,
∵∠CFG+∠FCD=y+z+80°-x=80°+m+40°+80°-m-20°=180°,
∴AB∥CD,
(3) 50°;70°;30°;10°.
解:(3) 当∠A=40°时,∠C=100°,
如图,分为四种情况:
延长FE交AM于N,
∵∠BAE=40°,∠BAM=20°,
∴∠MAE=20°,
∵∠AEF=80°,
∴∠ANE=80°-20°=60°,
∴∠AMF=60°-10°=50°,
∵∠AGF=∠MFE+∠AEF=10°+80°=90°,
∴∠AMF=90°-∠MAE=70°,
∵∠BAM=20°,∠BAE=40,°
∴∠EAM=60°,
∵∠AHF=∠MFE+∠AEF=90°,
∴∠AMF=90°-∠EAM=30°,
延长AE交FM于O,
∵∠AEF=∠EFO+∠AOF=80°,
∴∠AOF=80°-10°=70°,
∴∠AMF=∠AOF-∠MAF=70°-60°=10°,
综上所述:∠AMF的度数分别为:50°;70°;30°;10°.
(1)利用二次根式和绝对值的非负性解题即可;
(2)过点F作FG∥AB,点E作EH∥AB,则有EH∥FG,即可得到∠BAE=m+20°,∠EFG=∠FEH,求出∠EFG=60°-m,再根据∠CFG+∠FCD=180°,得到结论;
(3)分四种情况画图,利用角的和差得到∠MAE=20°,然后求出∠ANE和∠ANF的度数,利用三角形的内角和定理和外角性质解题即可
18.(1)解:,理由如下:
∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵平分,
∴,
∵,
∴,
∴.
(1)根据题意,先由平行线的判定得出,进而由平行线的性质得到,推出,即可得证;
(2)角平分线的定义,求出,平行线的性质,得到,即可解答.
19.解:,(已知),
(垂直的定义),
(同位角相等,两直线平行).
(两直线平行,同旁内角互补)
(已知).
(等量代换).
∴(内错角相等,两直线平行)
(两直线平行,同位角相等).
20.(1)解:∵,
∴,
∵,
∴
(2)解:∵平分交于点,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴
21.(1)证明:∵BC∥DF,
∴∠B+∠BFD=180°,
∵∠B=∠D,
∴∠D+∠BFD=180°,
∴AB∥CD,
∴∠A=∠ACD;
(2)解:∵∠A+∠B=108°,
∴∠ACB=72°,
∵FG∥AC,
∴∠BGF=72°,
∵BC∥DF,
∴∠EFG=72°.
(1)根据两直线平行,同旁内角互补得到∠B+∠BFD=180°,根据等量关系得到∠D+∠BFD=180°,即可得到AB∥CD证明结论;(2)利用三角形内角和定理求出∠ACB的度数,然后根据两直线平行,同位角相等求出∠BGF的度数,再根据两直线平行,内错角相等解题即可.
22.;两直线平行,同旁内角互补;;内错角相等,两直线平行;两直线平行,同位角相等
23.(1)解:如图,,
平分,
,
,
(2)解:如图
,
,
,
,
平分,
,
,
,
,
,
,
的度数为
(1)根据等边对等角得到,根据角平分线得到,即可得到,再根据平行线的判定定理得到结论即可;
(2)先得到,再根据两直线平行,内错角相等得到,根据角平分线的定义得到,求出∠3的度数,即可得到的度数解题.
24.解:(已知)
∠DCB =180°(两直线平行,同旁内角互补 )
(已知)
(等量代换)
∴CD//AB(同旁内角互补,两直线平行 )
∠4
(已知)
∠4(等量代换)
∴DE∥AC(内错角相等,两直线平行)
故答案为: 两直线平行,同旁内角互补,CD 同旁内角互补,两直线平行 两直线平行,内错角相等, 内错角相等,两直线平行.
由两直线平行,同旁内角互补得∠2+∠DCB=180°,由已知及等量代换得∠B+∠DCB=180°,由同旁内角互补,两直线平行,得CD//AB,根据二直线平行,内错角相等得∠3=∠4,由等量代换可得∠1=∠4,最后根据内错角相等,两直线平行,可证DE∥AC.
25.(1)解:AF∥DC,理由如下:
∵AC∥EF,
∴∠1+∠2=180°,
∵ ∠1+∠3=180°,
∴∠2=∠3,
∴AF∥CD.
(2)解:∵AC平分∠FAB,
∴∠2=∠CAD,
∵∠2=∠3,
∴∠3=∠CAD,
∵∠4=∠3+∠CAD=2∠3=80°,
∴∠3=40°,
∵AC∥EF,EF⊥BE ,
∴∠ACB=90°,
∴∠BCD=∠ACB-∠3=90°-40°=50°.
(1)由二直线平行,同旁内角互补得∠1+∠2=180°,结合已知,由同角的补角相等得∠2=∠3,再利用内错角相等,两直线平行,即证结论;
(2)由角平分线的定义及三角形外角的性质可求出∠3得度数,由平行线的性质及垂直定义可得∠ACB=90°,利用∠BCD=∠ACB-∠3即可求解.
26.(1)证明:∵ ,
∴∠AFD=∠AED.
∵,
∴∠AFD+∠FDE=180°,
∴∠AED+∠FDE=180°,
∴;
(2)解:∵,
∴,
由(1)可得:,DE//AB,
∴.
(1)根据平角的定义和 ,∠AFD=∠AED,再根据平行线的性质得∠AFD+∠FDE=180°,等量代换再结合平行线的判定方法即可得到结论;
(2)根据三角形内角和定理得出,利用两次平行线的性质即可得到结论。
(1)解:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
根据解析(1)可知:,,
∵,
∴,
∵,
∴.
27.(1)解:∵,
∴,
∵,
∴,
∴
(2)解:∵,∴,
∵,
∴,
∵,
∴,
∴
28.(1)
(2)
(3)存在,射线与相交所夹锐角的度数为或
29.已知;对顶角相等;;同旁内角互补,两直线平行
解:∵(已知),
(对顶角相等),
(等量代换).
又∵(已知),
∴,
∴(同旁内角互补,两直线平行).
故答案为:已知;对顶角相等;;同旁内角互补,两直线平行。
根据已知条件可得,由对顶角相等可得=110°,从而得到,进而根据同旁内角互补,两直线平行,即可得出结论.
30.证明:(已知),
∴(两直线平行,同位角相等),
(两直线平行,内错角相等).
(已知),
(等量代换).
平分(角平分线的定义).
故答案为:已知;;两直线平行,同位角相等;;两直线平行,内错角相等;,;角平分线的定义.
根据两直线平行,同位角相等得到∠B=∠DCE,根据两直线平行,内错角相等得∠A=∠ACE,结合已知条件,由等量代换得到∠ACE=∠DCE,根据角平分线的定义即可得到CE平分∠ACD.
期中真题专项复习12 证明题
一、证明题
1.(2024七下·温州期中)如图,已知,,,则.完成下面的说理过程.
解:(已知)
______(______)
(已知)
(等量代换)
______(______)
______(______)
(已知)
______(等量代换)
(______).
2.(2024七下·杭州期中)如图,已知 ,请你再画一个 ,使,,且交 边与点P.
(1)探究: 与有怎样的数量关系? 并说明理由.
(2)在(1)的条件下,若,求x、 y的值.
3.(2024七下·诸暨期中)如图,已知,,垂足分别为,F,,试说明.
将下面的解答过程补充完整.
证明:,(已知)
又
.
4.(2024七下·开化期中)如图,若,BD平分,则.完成下面的说理过程:
解:∵,
根据( )
得: .
再根据“两直线平行,内错角相等”,
得 .
∵BD平分,
∴ .
∴.
5.(2024七下·柯桥期中)如图,已知∠1=48°,∠2=132°,∠C=∠D.
(1)求证:BD∥CE;
(2)若∠A=40°,求∠F的度数.
6.(2024七下·浙江期中)根据推理过程,完成填空.
如图,已知,,.判断与是否垂直,并说明理由.
解:∵,(已知)
∴ ,(垂直的意义)
∴ .( )
∴,( )
又∵,(已知)
∴ .( )
∴.( )
∴ .(两直线平行,同位角相等)
7.(2024七下·修水期中) 如图,已知,.
(1)与平行吗?请说明理由.
(2)与的位置关系如何?为什么?
8.(2024七下·慈溪期中)如图,在四边形中,,.
(1)求的度数;
(2)若平分交于点,,求证:.
9.(2024七下·慈溪期中)如图,在中,平分,过点作交于点,过点作交于点,则可推得平分,其推导过程和推理依据如下:
解:,(已知)
▲ ( ▲ )
,(已知)
∴ ▲ =,( ▲ )
▲ .( ▲ )
.(等量代换)
又∵平分,(已知)
.( ▲ )
▲ .(等量代换)
∴平分.(角平分线定义)
请完善以上推导过程和推理依据,并按照顺序将相应内容填写在答题卡指定区域内.
10.(2024七下·义乌期中)如图,D是BC上一点,DE∥AB,交AC于点E,F是AB上一点,且∠DEC+∠AFD=180°.
(1)求证:DF∥AC;
(2)若∠B+∠C=130°,求∠FDE的度数.
11.(2024七下·拱墅期中)如图,已知,.
(1)与是否平行?请说明理由.
(2)与是否相等?请说明理由.
12.(2024七下·嘉善期中)如图,D,E分别在的边、上,F在线段上,且,.求证:.
13.(2024七下·拱墅期中)如图,在三角形中,D,E,F分别是上的点,且.
(1)若,试判断与是否垂直,并说明理由;
(2)若平分,,求的度数.
14.(2024七下·西湖期中)已知:点E在线段间(如图1).连接..
(1)求证:.
(2)如图2,点F在点E右侧.连接.
求证.
(3)如图3在(2)的条件下,线段,的延长线交于点H.交于点K.当平分,平分,,时,求的度数.
15.(2024七下·新昌期中)已知:如图,,,则.完成下面的说理过程(填空)
解:∵,(已知)
∴______(____________).
∵(____________),
∴______=______(等量代换).
∴(____________).
16.(2024七下·新昌期中)已知:如图,AB∥CD,∠A=∠D
则AF∥ED.完成下面的说理过程(填空)
解:∵AB∥CD,(已知)
∴∠A= ▲ .( )
∵∠A=∠D,( )
∴ ▲ = ▲ .(等式性质)
∴AF∥ED.( )
17.(2024七下·杭州期中)如图,∠AEF=80°,且∠A=x°,∠C=y°,∠F=z°.若+|y-80-m|+|z-40|=0(m为常数,且0<m<100)
(1) 求∠A、∠C的度数(用含m的代数式表示)
(2) 求证:AB∥CD
(3) 若∠A=40°,∠BAM=20°,∠EFM=10°,直线AM与直线FM交于点M,直接写出∠AMF的度数
18.(2024七下·温州期中) 如图,与相交于点F,,.
(1)试判断与的位置关系,并说明理由.
(2)若平分,,求的度数.
19.(2024七下·临海期中) 如图,已知,,垂足分别为D、F,,试说明:.请补充说明过程,并在括号内填上相应的理由.
解:,(已知),
(_▲_),
(_▲_).
_▲__(_▲_)
(已知).
(_▲_).
∴_▲_(_▲_)
(_▲_).
20.(2024七下·慈溪期中)如图,在四边形中,,.
(1)求的度数;
(2)若平分交于点,,求证:.
21.(2024七下·余杭期中)如图,已知BC∥DF,∠B=∠D,A、F、B三点共线,连接AC交DF于点E.
(1)求证:∠A=∠ACD.
(2)若FG∥AC,∠A+∠B=108°,求∠EFG的度数.
22.(2024七下·苍南期中)完成下面的证明过程.
如图,点D,G分别在三角形的边,上,于点E,于点F,连结.若,试说明的理由.
解:,
.
( ).
( ).
( ).
23.(2024七下·镇海区期中)如图,已知F,E分别是射线上的点.连接,其中平分,平分,.
(1)试说明;
(2)若,求的度数.
24.(2024七下·温州期中)如图,已知,则.完成下面的说理过程.
解:(已知)
▲ )
(已知)
(等量代换)
∴ ▲ //AB( )
▲
(已知)
▲ (等量代换)( )
∴DE∥AC( )
25.(2024七下·奉化期中)如图,AC∥EF,∠1+∠3=180°.
(1)判断AF与DC平行吗?请说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=80°,求∠BCD的度数.
26.(2024七下·义乌期中)如图,D是上一点,,交于点E,F是上一点,且.
(1)求证:;
(2)若,求的度数.
27.(2024七下·鄞州期中)如图,在三角形中,点D在上,交于点E,点F在,.
(1)试说明:;
(2)若,求的度数.
28.(2024七下·义乌期中)综合与实践数学社团的同学以“两条平行线,和一块含角的直角三角板”为主题开展数学活动,已知点E,F不能同时落在直线和之间.
(1)观察猜想:如图1,把三角板的角的顶点E,G分别放在,上,若,则的度数为______;(直接写出结论,不说明理由)
(2)类比探究:如图2,把三角板的锐角顶点G放在上,且保持不动,绕点G转动三角板,若点E恰好落在和之间,且与所夹锐角为,求的度数;
(3)解决问题:把三角板的锐角顶点放在上,在绕点旋转三角板的过程中,若存在,请直接写出射线与相交所夹锐角的度数.
29.(2024七下·镇海区期中)已知:如图,,判断.
下面是嘉琪同学的解题过程,请在括号中注明依据,在横线上补全步骤.
解:∵( ),
( ),
(等量代换).
又∵(已知),
∴ ,
∴( ).
30.(2024七下·路桥期中)如图,已知.求证:平分.
证明:( ),
▲ ( ),
▲ ( ),
(已知),
▲ = ▲ (等量代换).
平分( ),
答案解析部分
1.解:(已知)
(两直线平行,同旁内角互补)
(已知)
(等量代换)
(同旁内角互补,两直线平行)
(两直线平行,内错角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
根据题干信息提示,逐步完善推理过程与推理依据即可.
2.(1)解:与相等或互补,理由如下:
如图1,
,
,
,
,
,
如图2,
,
,
,
,
,
综上所述,与相等或互补;
(2)解:与相等或互补,
或,
,
或,
解得:或,
,或,.
(1)先分两种情况画图,利用平行线的性质解答即可;
(2)根据题(1)的结论列方程,再结合,解方程组求出x,y的值即可.
3.垂直定义;同位角相等,两直线平行;;已知;;;等量代换
4.两同旁内角互补,两直线平行;AB;CD;∠D;
解:∵,
根据两同旁内角互补,两直线平行,
得AB∥CD,
再根据“两直线平行,内错角相等”,
得
∵BD平分,
∴,
∴.
故答案为:两同旁内角互补,两直线平行;AB;CD;∠D;.
根据平行线的判定和性质以及角平分线的定义即可求解.
5.(1)证明:∵∠1=48°,∠2=132°,
∴∠1+∠2=180°,
∴BD∥CE;
(2)解:∵BD∥CE,
∴∠C=∠ABD,
又∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F=40°
(1)由“同旁内角互补,两直线平行”即可得到结论;
(2)由平行线的性质可得∠C=∠ABD,再结合 ∠C=∠D ,利用平行线的判定定理可得AC//DF,再由平行线的性质即可得到结论.
6.;同位角相等,两直线平行;两直线平行,内错角相等;;等量代换;同旁内角互补,两直线平行;
7.(1)解:与平行.
理由如下:
因为,,
所以,
所以.
(2)解:与平行.
理由如下:
因为,
所以.
因为,
所以.
所以.
(1)由邻补角的定义和 可得,根据平行线的判定定理即可得到结论.
(2)根据平行线的性质和等量代换得,根据平行线的判定定理可得到结论.
8.(1)解:解:,
,
,
,
的度数是110°;
(2)证明:∵平分交于点,=110°,
,
,
,
,
,
.
(1)根据平行线的性质得,最后进行计算即可求出答案;
(2)根据角平分线的定义求出∠DAE=55°,再根据平行线的性质得∠AEB=∠DAE=55°,从而得∠AEB=∠BCD,最后根据平行线的判定得AE∥CD.
9.解:,(已知)
(两直线平行,内错角相等)
,(已知)
∴=,(两直线平行,内错角相等)
(两直线平行,同位角相等;)
.(等量代换)
又∵平分,(已知)
.(角平分线定义)
∠BEF.(等量代换)
∴平分.(角平分线定义)
根据平行线的性质以及角平分线的定义即可得到答案.
10.(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
根据(1)可知:,,
∵,
∴,
∵,
∴.
(1)根据平行线的性质得到,进而结合题意得到,再根据平行线的判定即可求解;
(2)先根据题意得到,进而根据(1)可知:,,从而根据平行线的性质即可求解。
11.(1)解:,理由如下:
∵,
,
∴.
(2)解:,理由如下:
∵,
,
,
,
,
.
(1)根据“同角的补角相等”可得,然后根据"同位角相等两直线平行"可求解;
(2)先根据平行线的性质“两直线平行,内错角相等”可得,结合已知可得,然后根据"同位角相等两直线平行"可得,再根据平行线的性质“两直线平行,同位角相等”即可求解.
12.证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴.
先证明,可得,于是根据平行线的性质可得,再根据平行线性质得,等量代换即可证明结论.
13.(1)解:,理由如下:
,
,
∴∠BFD=∠FDE.
,
,
,
.
(2)解:平分,
,
,
,∠AFE=∠FED.
∵△FDE中,∠FDE+∠DFE+∠FED=2∠FDE+∠AFE=180°,
又∵∠FDE+3∠AFE=180°,
∴2∠FDE+∠AFE=∠FDE+3∠AFE,即∠FDE=2∠AFE.
∴5∠AFE=180°,
解得:∠AFE=36°,
∴∠BFE=2∠FDE=4∠AFE=144°.
14.(1)解:如图,过点E作,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:如图,过点F作,
∵,
∴,
∴,
∴,
即;
(3)解:设,∵平分,平分,
∴,
∴,
由(1)得:,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
解得:,
∴,
∴.
15.;两直线平行,内错角相等;已知;;;同位角相等,两直线平行
16.解:∵AB∥CD,(已知)
∴∠A=.(两直线平行,内错角相等)
∵∠A=∠D,(已知)
∴.(等式性质)
∴AF∥ED.(同位角相等,两直线平行)
由平行线的性质可得内错角相等,结合条件中的角度关系得到新的平行线.
17.(1) ∵+|y-80-m|+|z-40|=0(m为常数,且0<m<100),∴x-m-20=0,y-80-m=0,z-40=0,
∴∠A=x°=m+20°,∠C=y°=m+80°,z=40°,
(2) 过点F作FG∥AB,过点E作EH∥AB,
∴EH∥FG,
∴∠BAE=∠AEH=m+20°,∠EFG=∠FEH,
∴∠EFG=∠AEF-∠AEH=80°-(m+20°)=60°-m,
∵∠CFG+∠FCD=y+z+80°-x=80°+m+40°+80°-m-20°=180°,
∴AB∥CD,
(3) 50°;70°;30°;10°.
解:(3) 当∠A=40°时,∠C=100°,
如图,分为四种情况:
延长FE交AM于N,
∵∠BAE=40°,∠BAM=20°,
∴∠MAE=20°,
∵∠AEF=80°,
∴∠ANE=80°-20°=60°,
∴∠AMF=60°-10°=50°,
∵∠AGF=∠MFE+∠AEF=10°+80°=90°,
∴∠AMF=90°-∠MAE=70°,
∵∠BAM=20°,∠BAE=40,°
∴∠EAM=60°,
∵∠AHF=∠MFE+∠AEF=90°,
∴∠AMF=90°-∠EAM=30°,
延长AE交FM于O,
∵∠AEF=∠EFO+∠AOF=80°,
∴∠AOF=80°-10°=70°,
∴∠AMF=∠AOF-∠MAF=70°-60°=10°,
综上所述:∠AMF的度数分别为:50°;70°;30°;10°.
(1)利用二次根式和绝对值的非负性解题即可;
(2)过点F作FG∥AB,点E作EH∥AB,则有EH∥FG,即可得到∠BAE=m+20°,∠EFG=∠FEH,求出∠EFG=60°-m,再根据∠CFG+∠FCD=180°,得到结论;
(3)分四种情况画图,利用角的和差得到∠MAE=20°,然后求出∠ANE和∠ANF的度数,利用三角形的内角和定理和外角性质解题即可
18.(1)解:,理由如下:
∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵平分,
∴,
∵,
∴,
∴.
(1)根据题意,先由平行线的判定得出,进而由平行线的性质得到,推出,即可得证;
(2)角平分线的定义,求出,平行线的性质,得到,即可解答.
19.解:,(已知),
(垂直的定义),
(同位角相等,两直线平行).
(两直线平行,同旁内角互补)
(已知).
(等量代换).
∴(内错角相等,两直线平行)
(两直线平行,同位角相等).
20.(1)解:∵,
∴,
∵,
∴
(2)解:∵平分交于点,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴
21.(1)证明:∵BC∥DF,
∴∠B+∠BFD=180°,
∵∠B=∠D,
∴∠D+∠BFD=180°,
∴AB∥CD,
∴∠A=∠ACD;
(2)解:∵∠A+∠B=108°,
∴∠ACB=72°,
∵FG∥AC,
∴∠BGF=72°,
∵BC∥DF,
∴∠EFG=72°.
(1)根据两直线平行,同旁内角互补得到∠B+∠BFD=180°,根据等量关系得到∠D+∠BFD=180°,即可得到AB∥CD证明结论;(2)利用三角形内角和定理求出∠ACB的度数,然后根据两直线平行,同位角相等求出∠BGF的度数,再根据两直线平行,内错角相等解题即可.
22.;两直线平行,同旁内角互补;;内错角相等,两直线平行;两直线平行,同位角相等
23.(1)解:如图,,
平分,
,
,
(2)解:如图
,
,
,
,
平分,
,
,
,
,
,
,
的度数为
(1)根据等边对等角得到,根据角平分线得到,即可得到,再根据平行线的判定定理得到结论即可;
(2)先得到,再根据两直线平行,内错角相等得到,根据角平分线的定义得到,求出∠3的度数,即可得到的度数解题.
24.解:(已知)
∠DCB =180°(两直线平行,同旁内角互补 )
(已知)
(等量代换)
∴CD//AB(同旁内角互补,两直线平行 )
∠4
(已知)
∠4(等量代换)
∴DE∥AC(内错角相等,两直线平行)
故答案为: 两直线平行,同旁内角互补,CD 同旁内角互补,两直线平行 两直线平行,内错角相等, 内错角相等,两直线平行.
由两直线平行,同旁内角互补得∠2+∠DCB=180°,由已知及等量代换得∠B+∠DCB=180°,由同旁内角互补,两直线平行,得CD//AB,根据二直线平行,内错角相等得∠3=∠4,由等量代换可得∠1=∠4,最后根据内错角相等,两直线平行,可证DE∥AC.
25.(1)解:AF∥DC,理由如下:
∵AC∥EF,
∴∠1+∠2=180°,
∵ ∠1+∠3=180°,
∴∠2=∠3,
∴AF∥CD.
(2)解:∵AC平分∠FAB,
∴∠2=∠CAD,
∵∠2=∠3,
∴∠3=∠CAD,
∵∠4=∠3+∠CAD=2∠3=80°,
∴∠3=40°,
∵AC∥EF,EF⊥BE ,
∴∠ACB=90°,
∴∠BCD=∠ACB-∠3=90°-40°=50°.
(1)由二直线平行,同旁内角互补得∠1+∠2=180°,结合已知,由同角的补角相等得∠2=∠3,再利用内错角相等,两直线平行,即证结论;
(2)由角平分线的定义及三角形外角的性质可求出∠3得度数,由平行线的性质及垂直定义可得∠ACB=90°,利用∠BCD=∠ACB-∠3即可求解.
26.(1)证明:∵ ,
∴∠AFD=∠AED.
∵,
∴∠AFD+∠FDE=180°,
∴∠AED+∠FDE=180°,
∴;
(2)解:∵,
∴,
由(1)可得:,DE//AB,
∴.
(1)根据平角的定义和 ,∠AFD=∠AED,再根据平行线的性质得∠AFD+∠FDE=180°,等量代换再结合平行线的判定方法即可得到结论;
(2)根据三角形内角和定理得出,利用两次平行线的性质即可得到结论。
(1)解:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
根据解析(1)可知:,,
∵,
∴,
∵,
∴.
27.(1)解:∵,
∴,
∵,
∴,
∴
(2)解:∵,∴,
∵,
∴,
∵,
∴,
∴
28.(1)
(2)
(3)存在,射线与相交所夹锐角的度数为或
29.已知;对顶角相等;;同旁内角互补,两直线平行
解:∵(已知),
(对顶角相等),
(等量代换).
又∵(已知),
∴,
∴(同旁内角互补,两直线平行).
故答案为:已知;对顶角相等;;同旁内角互补,两直线平行。
根据已知条件可得,由对顶角相等可得=110°,从而得到,进而根据同旁内角互补,两直线平行,即可得出结论.
30.证明:(已知),
∴(两直线平行,同位角相等),
(两直线平行,内错角相等).
(已知),
(等量代换).
平分(角平分线的定义).
故答案为:已知;;两直线平行,同位角相等;;两直线平行,内错角相等;,;角平分线的定义.
根据两直线平行,同位角相等得到∠B=∠DCE,根据两直线平行,内错角相等得∠A=∠ACE,结合已知条件,由等量代换得到∠ACE=∠DCE,根据角平分线的定义即可得到CE平分∠ACD.
同课章节目录
