期中真题专项复习05解答题(含解析)--2024-2025学年八年级数学下册(人教版)
文档属性
| 名称 | 期中真题专项复习05解答题(含解析)--2024-2025学年八年级数学下册(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 907.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览



文档简介
2024-2025学年八年级数学下册(人教版)
期中真题专项复习05解答题
一、解答题
1.(2024八下·海淀期中)在平面直角坐标系中,对于线段,若在坐标系中存在一点P使得四边形为菱形,则称线段为点O的“关联线段”.
(1)已知点,则下列点N中,可以使得成为点O的“关联线段”的是 ;
①②③
(2)已知点O的“关联线段”过点,且,求出线段的最大值;
(3)已知点,若存在点O的“关联线段”与直线有交点,直接写出k的取值范围为 .
2.(2024八下·北京市期中)在平面直角坐标系中,对于点,,给出如下定义:当点,满足时,称点是点的等积点.已知点.
(1)在,,中,点的等积点是_____.
(2)点是点的等积点,点在轴上,以,,,为顶点的四边形是平行四边形,求点的坐标,写出求解过程.
3.(2024八下·北京市期中)已知直线经过点,.
(1)求直线的解析式;
(2)若直线与直线相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式的解集.
4.(2024八下·海淀期中)同学们,在二次根式一章中有一个有趣的现象:,根号里的因数2经过适当的演变,竟“跑”到了根号的外面,我们不妨把这种现象称为“穿墙”.具有这一性质的数还有许多,如、等等.
(1)猜想:______;
(2)请再写出1个具有“穿墙”性质的数______;
(3)请用只含有一个正整数的等式表示上述规律:______.
5.(2024八下·北京市期中)(1)观察,计算,判断:(只填写符号:,,
①当,时,__________;
②当,时,__________;
③当,时,__________;
…
(2)根据第(1)问,当,时,判断与的数量关系并证明,(提示:)
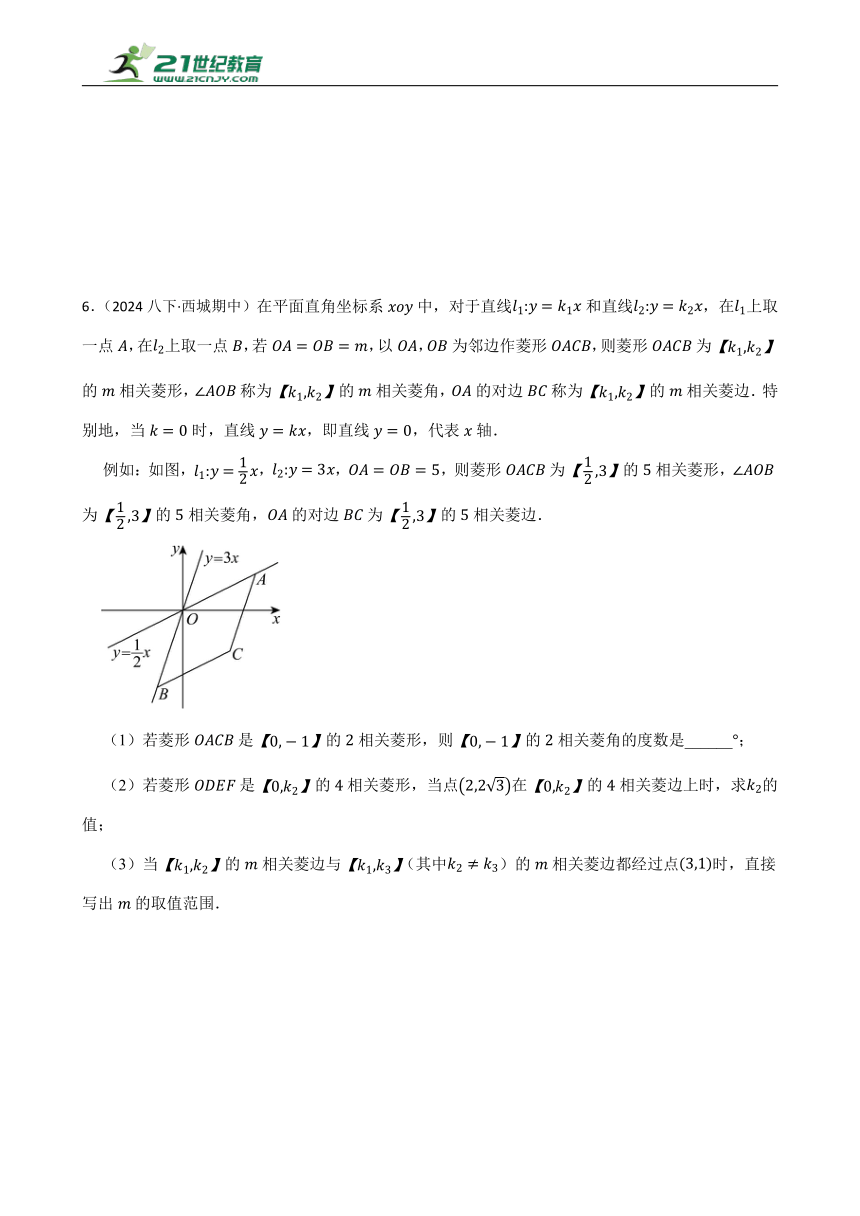
6.(2024八下·西城期中)在平面直角坐标系中,对于直线和直线,在上取一点,在上取一点,若,以,为邻边作菱形,则菱形为的相关菱形,称为的相关菱角,的对边称为的相关菱边.特别地,当时,直线,即直线,代表轴.
例如:如图,,,,则菱形为的相关菱形,为的相关菱角,的对边为的相关菱边.
(1)若菱形是的相关菱形,则的相关菱角的度数是______;
(2)若菱形是的相关菱形,当点在的相关菱边上时,求的值;
(3)当的相关菱边与(其中)的相关菱边都经过点时,直接写出的取值范围.
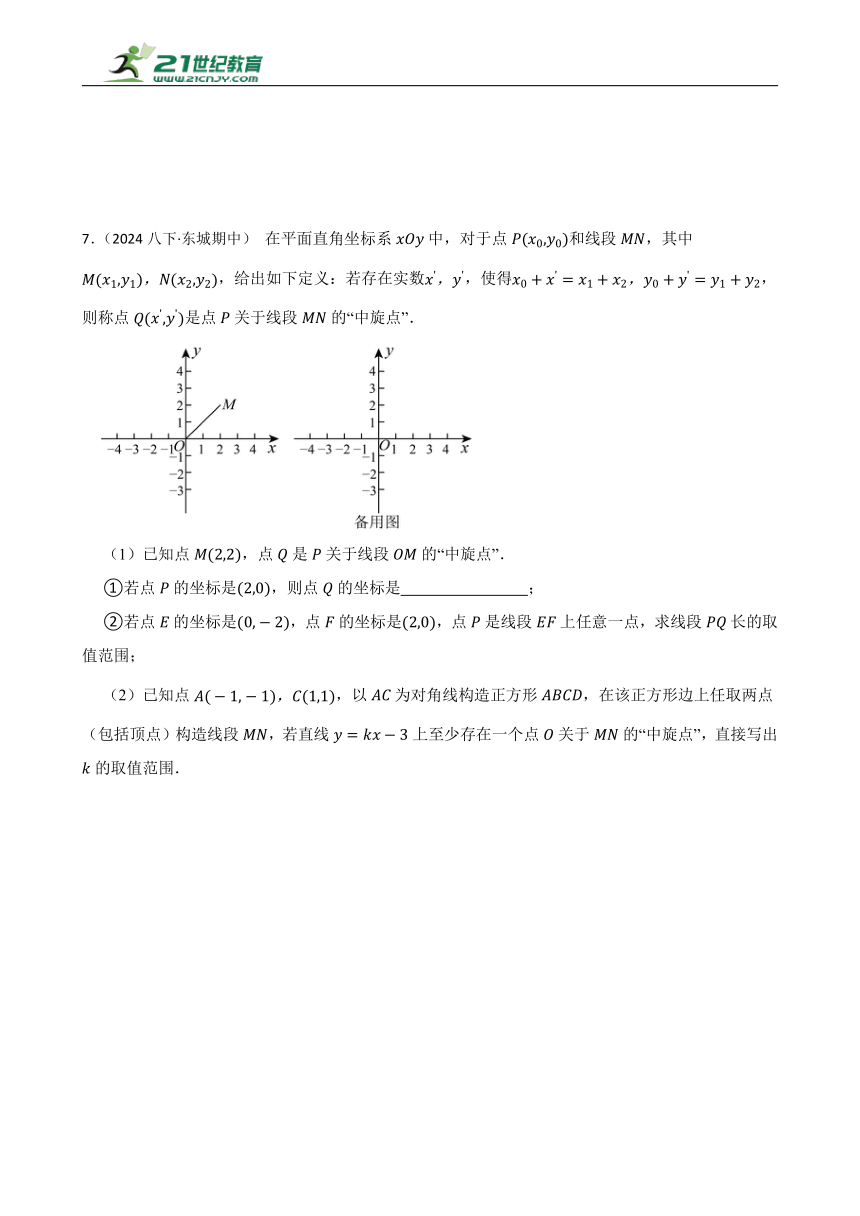
7.(2024八下·东城期中) 在平面直角坐标系中,对于点和线段,其中,给出如下定义:若存在实数,使得,则称点是点关于线段的“中旋点”.
(1)已知点,点是关于线段的“中旋点”.
①若点的坐标是,则点的坐标是 ;
②若点的坐标是,点的坐标是,点是线段上任意一点,求线段长的取值范围;
(2)已知点,以为对角线构造正方形,在该正方形边上任取两点(包括顶点)构造线段,若直线上至少存在一个点关于的“中旋点”,直接写出的取值范围.
8.(2024八下·东城期中) 如图,在等腰中,.点为的中点,动点从点出发,沿着方向运动至点处停止,过点作,交于点.设点运动的路程为,点的距离为.
(1)请直接写出关于的函数表达式,并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)解决问题:当点的距离恰好是点运动的路程的2倍时,点的距离是 .
9.(2024八下·卫东期中)如图,在四边形中,,,,动点P、Q分别从A、C同时出发,点P以的速度由A向D运动,点Q以的速度由C向B运动,其中一动点到达终点时,另一动点随之停止运动,设运动时间为t秒.
(1) , (分别用含有t的式子表示);
(2)当四边形的面积是四边形面积的2倍时,求出t的值.
(3)当点P、Q与四边形的任意两个顶点所形成的四边形是平行四边形时,直接写出t的值;
10.(2024八下·临邑期中)如图,直线过点、,直线和直线交于点,直线l2与y轴交于点.
(1)求直线和直线对应的函数解析式;
(2)直线上有一动点P,使得的面积为12,求点P的坐标;
(3)y轴上有一动点M,直线上有一动点N,使以M、N、A、B为顶点的四边形是平行四边形,求出点M的坐标.
11.(2024八下·汝阳期中)如图,一次函数与反比例函数的图象在第一象限交于点,连接交双曲线另一支于点.已知点的坐标为,分别过作轴于、轴与,连接,过作直线.
(1)求直线和反比例函数的表达式;
(2)点在双曲线上移动,其它条件不变,和的面积会改变吗?如果不会改变,请直接写出它们的面积;如果会改变,请说明理由.
12.(2024八下·商水期中)如图,在平面直角坐标系中,将一块等腰直角三角板放在第二象限,斜靠在两坐标轴上,点坐标为,点的坐标为,一次函数的图象经过点,,反比例函数图象也经过点.
(1)分别求出一次函数和反比例函数的解析式;
(2)直接写出当时,的解集;
(3)点是平面直角坐标系上任意一点,点是轴上一动点,当以点A、C、P、Q为顶点的四边形是菱形时,请直接写出点的坐标.
13.(2024八下·金水期中)如图,直线与y轴的交点为A,直线与直线的交点M的坐标为.
(1)__________,__________;
(2)直接写出关于x的不等式的解集__________;
(3)求的面积.
14.(2024八下·辉县市期中)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的两点,与轴交于点,点的坐标为,轴,且,.
(1)求反比例函数和一次函数的表达式;
(2)直接写出不等式的解集;
(3)是轴上一点,若的面积是的面积的2倍,求点的坐标.
15.(2024八下·大庆期中)已知四边形是边长为4的正方形,分别以所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过A、C两点.
(1)求直线l的函数表达式;
(2)如图2,若点D是的中点,E是直线l上的一个动点,求使取得最小值时点E的坐标.
(3)若P是直线l上的一个动点,请直接写出当是等腰三角形时点P的坐标.
16.(2024八下·大庆期中)解答以下各题
(1)已知a、b互为相反数,c、d互为倒数,x是3的平方根,求的值.
(2)已知,c是的立方根,求.
17.(2024八下·哈尔滨期中)如图,已知平面直角坐标系中,正比例函数的图象经过点.
(1)求的值;
(2)点是轴正半轴上一点,若,求线段的长.
18.(2024八下·哈尔滨期中)已知y=y1-2y2中,其中y1与x成正比例,y2与(x+1)成正比例,且当x=1时,y=3;当x=2时,y=5,
(1)求y与x的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
19.(2024八下·望奎期中)已知正比例函数y=kx图象经过点(3,-6),求:
(1)这个函数的解析式;
(2)判断点A(4,-2)是否在这个函数图象上.
(3)图象上的两点B(x1,y1)、C(x2,y2),如果x1>x2,比较y1,y2的大小.
20.(2024九上·高安期中)如图所示,四边形是证明勾股定理时用到的一个图形,a、b、c是和的边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.请解决下列问题:
(1)试判断方程是否为“勾系一元二次方程”.
(2)若是“勾系一元二次方程”的一个根,且四边形的周长是12,求的面积.
21.(2024八下·佳木斯期中)已知,在平面直角坐标系中,矩形的边在轴的正半轴上,边在轴的正半轴上,且点,,为上一点,将矩形沿翻折,使点落在边上的点处.
(1)求点的坐标;
(2)动点从点出发以每秒2个单位长度的速度沿轴向右运动,连接,设的面积为,点运动的时间为秒,请用含的式子表示的面积,并直接写出的取值范围;
(3)在平面内是否存在一点,使以,,,为顶点的四边形为平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
22.(2024八下·南岗期中)已知一次函数的图象过点与.
(1)求这个一次函数的解析式;
(2)当时,求的值.
23.(2024八下·安达期中)已知:,求代数式x2﹣y2+5xy的值.
24.(2024九上·顺义期中)在平面直角坐标系中,函数的图象经过点,,且与轴交于点.
(1)求该函数的解析式及点的坐标;
(2)当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.
25.(2024八下·遵化期中)如图,在平面直角坐标系中,过点的直线与直线相交于点,动点在直线上运动.求:
(1)直线的解析式;
(2)当的面积是的面积的时,求出这时点的坐标.
26.(2023八下·南江期中)已知一次函数y=kx-4,当x=2时,y=-3.
(1)求一次函数的表达式;
(2)将该函数的图象向上平移6个单位长度,求平移后的图像与x轴交点的坐标.
27.(2024八下·江门期中)为弘扬向善、为善优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在,爱心助力暖人心”慈善捐款活动,八年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是_______,并补全条形统计图;
(2)本次捐款金额的众数为______元,中位数为______元;
(3)若该校八年级学生为600名,请你估算捐款总金额约有多少元?
28.(2024八下·惠阳期中)已知是一次函数,且当时,当时.
(1)求这个一次函数的解析式;
(2)求当时,自变量的取值范围.
29.(2024八下·兴宁期中) 如图,已知函数的图像与轴交于点,一次函数的图像分别与轴、轴交于点B,C,且与的图像交于点D(m,4).
(1)求m,b的值;
(2)若,则的取值范围是;
(3)求四边形的面积.
30.(2024八下·荔湾期中)如图,某学校(A点)与公路(直线l)的距离为300米,到车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之到学校A及车站D的距离相等,求商店C与车站D之间的距离.
31.(2024八下·青秀期中) 如图,在矩形中,点在边上,点在的延长线上,且.
(1)求证:;
(2)连结,若平分,求证四边形的为菱形.
32.(2024八下·翔安期中)如图,在平面直角坐标系中,,,,,并且a、b满足.一动点P从点A出发,在线段上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段上以每秒1个单位长度的速度向点C运动,点分别从点同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒).
(1)求两点的坐标.
(2)当t为何值时,四边形是平行四边形?并求出此时两点的坐标.
(3)当t为何值时,是以为腰的等腰三角形?并求出两点的坐标.
33.(2024八下·涵江期中)如图,在珠海横琴一块三角形土地上,准备规划出阴影所示部分作为绿地,若规划图设计中∠ADC=90°,AD=8,CD=6,AB=26,BC=24,求绿地的面积.
34.(2024八下·巴林右旗期中)已知与x成正比例,与成正比例,当时,;当时,.
(1)求y与x的函数解析式;
(2)当时,求y的值.
35.(2024八下·平潭期中)如图1,将矩形放置于第一象限,使其顶点O位于原点,且点B,C分别位于x轴,y轴上. 若满足;
(1)求点A的坐标;
(2)取中点,连接,与关于所在直线对称,连接并延长, 交x轴于点P.
①求的长;
②如图2,点D位于线段上,且.点E为平面内一动点,满足, 连.请你求出线段长度的最大值.
36.(2024八下·蒸湘期中)已知一次函数.
(1)当m为何值时,这个函数为正比例函数
(2)当m为何值时,这个函数y的值随着x值的增大而减小
37.(2024八下·平果期中)已知a,b,c满足.
(1)求a,b,c的值;
(2)试问:长为a,b,c的三条线段能否构成直角三角形?若能构成直角三角形,请说明理由;若不能构成直角三角形,请说明理由.
38.(2024八下·梁平期中) “儿童做学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节,某校八年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度,他们进行了如下操作:①测得水平距离的长为15米;②根据手中剩余线的长度计算出风筝线的长为17米;③牵线放风筝的小明放风筝时手距离地面1.7米.
(1)求风筝的垂直高度;
(2)如果小明想让风筝沿方向再上升12米,长度不变,则他应该把线再放出多少米?
39.(2024八下·巨野期中)已知一次函数的图象经过点和点.
(1)求直线的解析式;
(2)求图像与x轴、y轴的交点C、D的坐标,并求出直线与坐标轴所围成三角形的面积;
(3)如果点和在直线上,求a,b的值.
40.(2024八下·姑苏期中)如图,正方形,边长为,动点从点以每秒的速度沿向运动,动点从点以每秒的速度沿向运动,连结.两点同时出发,设运动时间为秒.
(1)求运动时间为何值时的面积为;
(2)连结、,是否存在某一时刻,使为等腰三角形,若存在,求出所有的值;若不存在,请说明理由.
41.(2024八下·通州期中)如图1,平面直角坐标系中,过点分别作轴、轴的垂线,垂足分别为,两点,直线与交于点,与轴交于点.
(1)求点D的坐标;
(2)如图2,是线段上的一个动点(不与点重合),过作的垂线交于点.
①若,求的长;
②若的平分线与射线交于点,,,求关于的函数解析式.
答案解析部分
1.(1)①③
(2)
(3)
2.(1)和
(2)或
3.(1)
(2)
(3)
4.(1)
(2)(答案不唯一,符合规律即可)
(3)
5.(1),,;(2)
6.(1)或
(2)的值为
(3)
7.(1)解:①②设直线解析式为,∴,∴,∴直线解析式为,
∵点是线段上任意一点,∴可设,
∵点是关于线段的“中旋点”.∴,∴,∴,
∴,
令,∴,
∵,∴,
∴当时,的值随着m增大而减小,
∴当时,有最大值,当时,有最小值8,∴;
(2)或.
解:(2)如图2-1所示,当点M在上,点N在上时,
设,
∴,
∴,
∴
当点M固定时,点N从点C运动到点D,那么点Q的纵坐标不变,横坐标从0运动到,
当点N固定时,点M从点A运动到点D,那么点Q的横坐标不变,纵坐标从0运动到2,
∴当点M在上,点N在上时,点Q的运动区域即为四个点组成的正方形区域(不包括顶点E),
同理由对称性可知当点M与点N在正方形的邻边上时,点Q的运动区域为组成的正方形区域(不包括四个顶点);
如图2-2所示,当点M在上,点N在上时,
设,
∴,
∴,
∴
当点M固定时,点N从点C运动到点D,那么点Q的纵坐标不变,横坐标从运动到,
当点N固定时,点M从点A运动到点D,那么点Q的纵坐标不变,横坐标从运动到,
∴当点M在上,点N在上时,点Q的运动区域即为线段;
同理由对称性可知当点M在上,点N在上时,点Q的运动区域为线段;
当点M和点N都在上时,设,同理得,
∴此时点Q的运功区域为线段(不包括端点),
由对称性可知,当M、N在同一边时,点Q的运动区域即为线段(不包括端点),
综上所述,点Q的运动区域为组成的正方形区域(不包括四个顶点);
∵直线上至少存在一个点关于的“中旋点”,
∴直线与组成的正方形区域至少有一个交点(不包括顶点),
当直线恰好经过时,,解得;
当直线恰好经过时,,解得;
∴如图2-3所示,当或直线与组成的正方形区域至少有一个交点(不包括顶点),
∴若直线上至少存在一个点关于的“中旋点”,则或.
(1)①根据中旋点的定义,即可得出点Q的坐标;
②首先利用待定系数法求出直线EF的解析式,可设点P, 根据中旋点的定义,可得点Q(2-m,4-m),可得:PQ2=8(m-2)2+8,根据二次函数的性质,即可求得PQ的取值范围;
(2)首先分成两种情况讨论:当点M在上,点N在上时,可得点Q的运动区域为组成的正方形区域(不包括四个顶点);当点M在上,点N在上时,点Q的运动区域为组成的正方形区域(不包括四个顶点);综上所述,点Q的运动区域为组成的正方形区域(不包括四个顶点);然后根据直线上至少存在一个点关于的“中旋点”,可得直线与组成的正方形区域至少有一个交点(不包括顶点),当直线恰好经过时,,解得;当直线恰好经过时,,解得;结合图象可得出若直线上至少存在一个点关于的“中旋点”,则或.
8.(1)解:,
,
点为的中点,
,
当点在上运动时,,
,
由题意得:,则,
,,
,
;
当点在上运动时,,
,
由题意得:,则,
,,
,
;
综上所述,;
(2)解:画出函数图象如图所示:
,
由图象可得,函数的最大值为;
(3)
解:(3)可分成两种情况:①当当点在上运动时,,2x=,解得:x=,所以y=,即 点的距离是;② 当点在上运动时,, 2x=,解得:x=(不合题意,舍去);综上可得: 点的距离是;
故答案为:;
(1)关于的函数表达式 可分为两段来表示:① 当点在上运动时,,可得出BP=2+x, 根据含30°锐角的直角三角形的性质,可得出; ② 当点在上运动时,, 可得出CP=6-x,从而根据含30°锐角的直角三角形的性质,可得出;综上所述,可得出:;
(2)根据界点,分别描出点(0,1),(2,2)及(6,0),连接(0,1),(2,2),再连接(2,2),(6,0),即可得出函数图象,观察函数图象,可得函数的最大值为2;
(3)可分成两种情况:①当当点在上运动时,,2x=,解得:x=,所以y=,即 点的距离是;② 当点在上运动时,, 2x=,解得:x=(不合题意,舍去);综上可得: 点的距离是;
9.(1),
(2)
(3)或或
10.(1)直线的函数解析式为,直线对应的函数解析式为
(2)P的坐标为或
(3)M的坐标为或或
11.(1)直线表达式为,反比例函数的表达式为;
(2)不会改变,的面积是,的面积是.
12.(1),
(2)
(3)点坐标为或或或
13.(1)3,1
(2)
(3)
14.(1),
(2)或
(3)点的坐标为或
15.(1)
(2)
(3),,
16.(1)0或
(2)2
17.(1)
(2)
18.(1) ;(2)1
19.(1) ;(2) A(4,-2)不在这个函数图象上;(3) y120.(1)是勾系一元二次方程;
(2)2.
21.(1)
(2)
(3)或或
22.(1)这个一次函数的解析式为
(2)
23.
24.(1)解:将,代入函数解析式得,
,
解得,
∴函数的解析式为:,
当时,得,
∴点A的坐标为.
(2)解:n的取值范围为:.
解:(2)由题意得,
,即,
又由,得,
解得,
∴的取值范围为.
(1)将点(4,3)与(-2,0)分别代入y=kx+b中,可得关于字母k、b的二元一次方程组,求解得出k、b的值,即可得到所求的函数解析式;然后令所求函数解析式中的x=0,求出对应的y的值,即可得到点A的坐标;
(2)根据题意结合解出不等式即可求解.
25.(1)设直线的解析式是,
根据题意得:,解得:,
则直线的解析式是;
(2),当时,,
,,的面积为;
设点的坐标为,,
解得或,
当时,,
当时,,
则点的坐标为或.
本题考查两条直线相交问题,用待定系数法求一次函数的解析式、坐标与图形性质以及三角形面积求法.
(1)设直线的解析式是,将点代入函数解析式可列出方程组,解方程组可求出的值,据此可求出解析式;
(2)当时,可求出点的坐标,利用三角形的面积公式求出的面积,再根据面积公式可求出点的横坐标,再代入解析式可求出点的纵坐标,据此可求出点的坐标.
26.(1)y=x-4.(2)(-4,0).
27.(1)50,
“捐款为15元”的学生有(人),补全条形统计图如下:
(2)15,15;
(3)解:样本平均数为(元/人),
∴全校八年级学生为600名,捐款总金额为(元),
答:全校八年级学生为600名,捐款总金额为8040元.
(1)解:(人),
(2)解:学生捐款金额出现次数最多的是15元,共出现18次,因此捐款金额的众数是15元,
将这50名学生捐款金额从小到大排列处在中间位置的两个数都是15元,因此中位数是15元,
故答案为:15,15.
(1)利用“A”的人数除以对应的百分比可得总人数,再求出“C”的人数并作出条形统计图即可;
(2)利用众数和中位数的定义及计算方法分析求解即可;
(3)先求出样本的平均数,再乘以总人数可得答案.
28.解:(1)设一次函数的解析式为=kx+b,
∵ 当时,当时.
∴
解得:
∴这个一次函数的解析式为:
(2))∵k=-1,∴y随x的增大而减小,
∴当y=-3时,-3=-x+5,x=8;当y=1时,1=-x+5,x=4
∴当时自变量x的取值范围是:.
(1)首先设出这个一次函数的解析式为y=kx+b(k≠0),再利用待定系数法可得方程组,再解方程组可得k、b的值,进而把得k、b的值代入解析式即可得;
(2)根据k=-1<0可得y随x的增大而减小,然后计算出y=-3时x的值,y=1时x的值,进而得到x的取值范围.
29.(1)解:∵函数y1=x+5的图象与x轴交于点A,
∴A(-5,0).
∵y=4时,x+5=4,解得x=-1,
∴D(-1,4).
将D(-1,4)代入y2=-2x+b,
得4=-2×(-1)+b,
解得b=2,
故m=-1,b=2;
(2)解:由图象可知,若y1>y2,则x的取值范围是x>-1.
故答案为x>-1;
(3)解:∵一次函数y2=-2x+2的图象分别与x轴、y轴交于点B,C,
∴B(1,0),C(0,2),
∴S四边形AOCD=S△ABD-S△BOC
=×6×4-×1×2
=12-1
=11.
(1)利用一次函数与坐标轴相交特点求得点A,D的坐标,再利用待定系数法求得b的值,即可求解;
(2)通关观察图象即可求解;
(3)先求的B,C两点的坐标,再根据S四边形AOCD=S△ABD-S△BOC代入数据计算即可求解.
30.解:作AB⊥l于B,则AB=300m,AD=500m.
∴∠ABD=90°,
在Rt△ABD中,
∴m.
设CD=AC=x,则CB=400﹣x,
x2=(400﹣x)2+3002,
x2=160000+x2﹣800x+3002,
800x=250000,
x=312.5m.
答:商店与车站之间的距离为312.5米.
作AB⊥l于B,则AB=300m,AD=500m,在Rt△ABD中,由勾股定理得BD=400m,设CD=AC=x,则CB=400﹣x,在Rt△ABC中,利用勾股定理建立方程可求出x的值,从而即可得出答案.
31.(1)证明:四边形为矩形,
,,
,
;
(2)证明:如图,连接.
,
,,
∴,
四边形是平行四边形.
平分,
,
∵,
,
,
,
四边形是菱形.
(1)由平行四边形的性质得:AB=DC,∠B=∠DCF,结合已知,用边角边可证得△ABE≌△DCF;
(2)连接DE,由(1)中的全等三角形可得AE=DF,∠AEB=∠F,由平行线的判定可得AE∥DF,根据一组对边平行且相等的四边形是平行四边形可得四边形AEFD是平行四边形,由角平分线的定义和平行线的性质可得∠ADE=∠AED,由等角对等边可得AE=AD,根据有一组邻边相等的平行四边形是菱形可求解.
32.(1),
(2)当时,四边形是平行四边形;,
(3)或;,,或,
33.绿地的面积为96
34.(1)
(2)y的值为
35.(1)
(2)①;②
36.(1)解:.
∵函数为正比例函数,
∴,
解得:,
答:当时,这个函数为正比例函数
(2)解:一次函数.
∵函数y的值随着x值的增大而减小,
∴,
答:当时,函数y的值随着x值的增大而减小.
(1)根据正比例函数的定义,即可得出,解方程即可得出m的值;
(2)根据一次函数的性质,即可得出m<0.
37.(1)解:,
∴,
∴,,
(2)解:∵,,,
∴,
∵,
∴长为a,b,c的三条线段不能构成直角三角形.
(1)根据偶次方的非负性、绝对值的非负性、算术平方根的非负性,且这三个非负项之和为0,所以每一项都必须等于0,分别建立方程求解即可;
(2)分别计算,进而根据勾股定理的逆定理进行判断,即可求解.
38.(1)解:∵米,米
∴根据勾股定理可得(米),
由题可知,米,
∴米;
(2)解:根据勾股定理可得:放出后(米),
即他应该放出8米.
(1)先利用勾股定理求出AC的长,再利用线段的和差求出AD的长即可;
(2)先利用勾股定理求出AB的长,再列出算式求解即可.
39.(1);(2),;(3),.
40.(1)运动时间时的面积为
(2)或或或时,为等腰三角形
41.(1)
(2)①的长为2;②
期中真题专项复习05解答题
一、解答题
1.(2024八下·海淀期中)在平面直角坐标系中,对于线段,若在坐标系中存在一点P使得四边形为菱形,则称线段为点O的“关联线段”.
(1)已知点,则下列点N中,可以使得成为点O的“关联线段”的是 ;
①②③
(2)已知点O的“关联线段”过点,且,求出线段的最大值;
(3)已知点,若存在点O的“关联线段”与直线有交点,直接写出k的取值范围为 .
2.(2024八下·北京市期中)在平面直角坐标系中,对于点,,给出如下定义:当点,满足时,称点是点的等积点.已知点.
(1)在,,中,点的等积点是_____.
(2)点是点的等积点,点在轴上,以,,,为顶点的四边形是平行四边形,求点的坐标,写出求解过程.
3.(2024八下·北京市期中)已知直线经过点,.
(1)求直线的解析式;
(2)若直线与直线相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式的解集.
4.(2024八下·海淀期中)同学们,在二次根式一章中有一个有趣的现象:,根号里的因数2经过适当的演变,竟“跑”到了根号的外面,我们不妨把这种现象称为“穿墙”.具有这一性质的数还有许多,如、等等.
(1)猜想:______;
(2)请再写出1个具有“穿墙”性质的数______;
(3)请用只含有一个正整数的等式表示上述规律:______.
5.(2024八下·北京市期中)(1)观察,计算,判断:(只填写符号:,,
①当,时,__________;
②当,时,__________;
③当,时,__________;
…
(2)根据第(1)问,当,时,判断与的数量关系并证明,(提示:)
6.(2024八下·西城期中)在平面直角坐标系中,对于直线和直线,在上取一点,在上取一点,若,以,为邻边作菱形,则菱形为的相关菱形,称为的相关菱角,的对边称为的相关菱边.特别地,当时,直线,即直线,代表轴.
例如:如图,,,,则菱形为的相关菱形,为的相关菱角,的对边为的相关菱边.
(1)若菱形是的相关菱形,则的相关菱角的度数是______;
(2)若菱形是的相关菱形,当点在的相关菱边上时,求的值;
(3)当的相关菱边与(其中)的相关菱边都经过点时,直接写出的取值范围.
7.(2024八下·东城期中) 在平面直角坐标系中,对于点和线段,其中,给出如下定义:若存在实数,使得,则称点是点关于线段的“中旋点”.
(1)已知点,点是关于线段的“中旋点”.
①若点的坐标是,则点的坐标是 ;
②若点的坐标是,点的坐标是,点是线段上任意一点,求线段长的取值范围;
(2)已知点,以为对角线构造正方形,在该正方形边上任取两点(包括顶点)构造线段,若直线上至少存在一个点关于的“中旋点”,直接写出的取值范围.
8.(2024八下·东城期中) 如图,在等腰中,.点为的中点,动点从点出发,沿着方向运动至点处停止,过点作,交于点.设点运动的路程为,点的距离为.
(1)请直接写出关于的函数表达式,并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)解决问题:当点的距离恰好是点运动的路程的2倍时,点的距离是 .
9.(2024八下·卫东期中)如图,在四边形中,,,,动点P、Q分别从A、C同时出发,点P以的速度由A向D运动,点Q以的速度由C向B运动,其中一动点到达终点时,另一动点随之停止运动,设运动时间为t秒.
(1) , (分别用含有t的式子表示);
(2)当四边形的面积是四边形面积的2倍时,求出t的值.
(3)当点P、Q与四边形的任意两个顶点所形成的四边形是平行四边形时,直接写出t的值;
10.(2024八下·临邑期中)如图,直线过点、,直线和直线交于点,直线l2与y轴交于点.
(1)求直线和直线对应的函数解析式;
(2)直线上有一动点P,使得的面积为12,求点P的坐标;
(3)y轴上有一动点M,直线上有一动点N,使以M、N、A、B为顶点的四边形是平行四边形,求出点M的坐标.
11.(2024八下·汝阳期中)如图,一次函数与反比例函数的图象在第一象限交于点,连接交双曲线另一支于点.已知点的坐标为,分别过作轴于、轴与,连接,过作直线.
(1)求直线和反比例函数的表达式;
(2)点在双曲线上移动,其它条件不变,和的面积会改变吗?如果不会改变,请直接写出它们的面积;如果会改变,请说明理由.
12.(2024八下·商水期中)如图,在平面直角坐标系中,将一块等腰直角三角板放在第二象限,斜靠在两坐标轴上,点坐标为,点的坐标为,一次函数的图象经过点,,反比例函数图象也经过点.
(1)分别求出一次函数和反比例函数的解析式;
(2)直接写出当时,的解集;
(3)点是平面直角坐标系上任意一点,点是轴上一动点,当以点A、C、P、Q为顶点的四边形是菱形时,请直接写出点的坐标.
13.(2024八下·金水期中)如图,直线与y轴的交点为A,直线与直线的交点M的坐标为.
(1)__________,__________;
(2)直接写出关于x的不等式的解集__________;
(3)求的面积.
14.(2024八下·辉县市期中)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的两点,与轴交于点,点的坐标为,轴,且,.
(1)求反比例函数和一次函数的表达式;
(2)直接写出不等式的解集;
(3)是轴上一点,若的面积是的面积的2倍,求点的坐标.
15.(2024八下·大庆期中)已知四边形是边长为4的正方形,分别以所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过A、C两点.
(1)求直线l的函数表达式;
(2)如图2,若点D是的中点,E是直线l上的一个动点,求使取得最小值时点E的坐标.
(3)若P是直线l上的一个动点,请直接写出当是等腰三角形时点P的坐标.
16.(2024八下·大庆期中)解答以下各题
(1)已知a、b互为相反数,c、d互为倒数,x是3的平方根,求的值.
(2)已知,c是的立方根,求.
17.(2024八下·哈尔滨期中)如图,已知平面直角坐标系中,正比例函数的图象经过点.
(1)求的值;
(2)点是轴正半轴上一点,若,求线段的长.
18.(2024八下·哈尔滨期中)已知y=y1-2y2中,其中y1与x成正比例,y2与(x+1)成正比例,且当x=1时,y=3;当x=2时,y=5,
(1)求y与x的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
19.(2024八下·望奎期中)已知正比例函数y=kx图象经过点(3,-6),求:
(1)这个函数的解析式;
(2)判断点A(4,-2)是否在这个函数图象上.
(3)图象上的两点B(x1,y1)、C(x2,y2),如果x1>x2,比较y1,y2的大小.
20.(2024九上·高安期中)如图所示,四边形是证明勾股定理时用到的一个图形,a、b、c是和的边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.请解决下列问题:
(1)试判断方程是否为“勾系一元二次方程”.
(2)若是“勾系一元二次方程”的一个根,且四边形的周长是12,求的面积.
21.(2024八下·佳木斯期中)已知,在平面直角坐标系中,矩形的边在轴的正半轴上,边在轴的正半轴上,且点,,为上一点,将矩形沿翻折,使点落在边上的点处.
(1)求点的坐标;
(2)动点从点出发以每秒2个单位长度的速度沿轴向右运动,连接,设的面积为,点运动的时间为秒,请用含的式子表示的面积,并直接写出的取值范围;
(3)在平面内是否存在一点,使以,,,为顶点的四边形为平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
22.(2024八下·南岗期中)已知一次函数的图象过点与.
(1)求这个一次函数的解析式;
(2)当时,求的值.
23.(2024八下·安达期中)已知:,求代数式x2﹣y2+5xy的值.
24.(2024九上·顺义期中)在平面直角坐标系中,函数的图象经过点,,且与轴交于点.
(1)求该函数的解析式及点的坐标;
(2)当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.
25.(2024八下·遵化期中)如图,在平面直角坐标系中,过点的直线与直线相交于点,动点在直线上运动.求:
(1)直线的解析式;
(2)当的面积是的面积的时,求出这时点的坐标.
26.(2023八下·南江期中)已知一次函数y=kx-4,当x=2时,y=-3.
(1)求一次函数的表达式;
(2)将该函数的图象向上平移6个单位长度,求平移后的图像与x轴交点的坐标.
27.(2024八下·江门期中)为弘扬向善、为善优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在,爱心助力暖人心”慈善捐款活动,八年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是_______,并补全条形统计图;
(2)本次捐款金额的众数为______元,中位数为______元;
(3)若该校八年级学生为600名,请你估算捐款总金额约有多少元?
28.(2024八下·惠阳期中)已知是一次函数,且当时,当时.
(1)求这个一次函数的解析式;
(2)求当时,自变量的取值范围.
29.(2024八下·兴宁期中) 如图,已知函数的图像与轴交于点,一次函数的图像分别与轴、轴交于点B,C,且与的图像交于点D(m,4).
(1)求m,b的值;
(2)若,则的取值范围是;
(3)求四边形的面积.
30.(2024八下·荔湾期中)如图,某学校(A点)与公路(直线l)的距离为300米,到车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之到学校A及车站D的距离相等,求商店C与车站D之间的距离.
31.(2024八下·青秀期中) 如图,在矩形中,点在边上,点在的延长线上,且.
(1)求证:;
(2)连结,若平分,求证四边形的为菱形.
32.(2024八下·翔安期中)如图,在平面直角坐标系中,,,,,并且a、b满足.一动点P从点A出发,在线段上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段上以每秒1个单位长度的速度向点C运动,点分别从点同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒).
(1)求两点的坐标.
(2)当t为何值时,四边形是平行四边形?并求出此时两点的坐标.
(3)当t为何值时,是以为腰的等腰三角形?并求出两点的坐标.
33.(2024八下·涵江期中)如图,在珠海横琴一块三角形土地上,准备规划出阴影所示部分作为绿地,若规划图设计中∠ADC=90°,AD=8,CD=6,AB=26,BC=24,求绿地的面积.
34.(2024八下·巴林右旗期中)已知与x成正比例,与成正比例,当时,;当时,.
(1)求y与x的函数解析式;
(2)当时,求y的值.
35.(2024八下·平潭期中)如图1,将矩形放置于第一象限,使其顶点O位于原点,且点B,C分别位于x轴,y轴上. 若满足;
(1)求点A的坐标;
(2)取中点,连接,与关于所在直线对称,连接并延长, 交x轴于点P.
①求的长;
②如图2,点D位于线段上,且.点E为平面内一动点,满足, 连.请你求出线段长度的最大值.
36.(2024八下·蒸湘期中)已知一次函数.
(1)当m为何值时,这个函数为正比例函数
(2)当m为何值时,这个函数y的值随着x值的增大而减小
37.(2024八下·平果期中)已知a,b,c满足.
(1)求a,b,c的值;
(2)试问:长为a,b,c的三条线段能否构成直角三角形?若能构成直角三角形,请说明理由;若不能构成直角三角形,请说明理由.
38.(2024八下·梁平期中) “儿童做学归来早,忙趁东风放纸鸢”.又到了放风筝的最佳时节,某校八年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度,他们进行了如下操作:①测得水平距离的长为15米;②根据手中剩余线的长度计算出风筝线的长为17米;③牵线放风筝的小明放风筝时手距离地面1.7米.
(1)求风筝的垂直高度;
(2)如果小明想让风筝沿方向再上升12米,长度不变,则他应该把线再放出多少米?
39.(2024八下·巨野期中)已知一次函数的图象经过点和点.
(1)求直线的解析式;
(2)求图像与x轴、y轴的交点C、D的坐标,并求出直线与坐标轴所围成三角形的面积;
(3)如果点和在直线上,求a,b的值.
40.(2024八下·姑苏期中)如图,正方形,边长为,动点从点以每秒的速度沿向运动,动点从点以每秒的速度沿向运动,连结.两点同时出发,设运动时间为秒.
(1)求运动时间为何值时的面积为;
(2)连结、,是否存在某一时刻,使为等腰三角形,若存在,求出所有的值;若不存在,请说明理由.
41.(2024八下·通州期中)如图1,平面直角坐标系中,过点分别作轴、轴的垂线,垂足分别为,两点,直线与交于点,与轴交于点.
(1)求点D的坐标;
(2)如图2,是线段上的一个动点(不与点重合),过作的垂线交于点.
①若,求的长;
②若的平分线与射线交于点,,,求关于的函数解析式.
答案解析部分
1.(1)①③
(2)
(3)
2.(1)和
(2)或
3.(1)
(2)
(3)
4.(1)
(2)(答案不唯一,符合规律即可)
(3)
5.(1),,;(2)
6.(1)或
(2)的值为
(3)
7.(1)解:①②设直线解析式为,∴,∴,∴直线解析式为,
∵点是线段上任意一点,∴可设,
∵点是关于线段的“中旋点”.∴,∴,∴,
∴,
令,∴,
∵,∴,
∴当时,的值随着m增大而减小,
∴当时,有最大值,当时,有最小值8,∴;
(2)或.
解:(2)如图2-1所示,当点M在上,点N在上时,
设,
∴,
∴,
∴
当点M固定时,点N从点C运动到点D,那么点Q的纵坐标不变,横坐标从0运动到,
当点N固定时,点M从点A运动到点D,那么点Q的横坐标不变,纵坐标从0运动到2,
∴当点M在上,点N在上时,点Q的运动区域即为四个点组成的正方形区域(不包括顶点E),
同理由对称性可知当点M与点N在正方形的邻边上时,点Q的运动区域为组成的正方形区域(不包括四个顶点);
如图2-2所示,当点M在上,点N在上时,
设,
∴,
∴,
∴
当点M固定时,点N从点C运动到点D,那么点Q的纵坐标不变,横坐标从运动到,
当点N固定时,点M从点A运动到点D,那么点Q的纵坐标不变,横坐标从运动到,
∴当点M在上,点N在上时,点Q的运动区域即为线段;
同理由对称性可知当点M在上,点N在上时,点Q的运动区域为线段;
当点M和点N都在上时,设,同理得,
∴此时点Q的运功区域为线段(不包括端点),
由对称性可知,当M、N在同一边时,点Q的运动区域即为线段(不包括端点),
综上所述,点Q的运动区域为组成的正方形区域(不包括四个顶点);
∵直线上至少存在一个点关于的“中旋点”,
∴直线与组成的正方形区域至少有一个交点(不包括顶点),
当直线恰好经过时,,解得;
当直线恰好经过时,,解得;
∴如图2-3所示,当或直线与组成的正方形区域至少有一个交点(不包括顶点),
∴若直线上至少存在一个点关于的“中旋点”,则或.
(1)①根据中旋点的定义,即可得出点Q的坐标;
②首先利用待定系数法求出直线EF的解析式,可设点P, 根据中旋点的定义,可得点Q(2-m,4-m),可得:PQ2=8(m-2)2+8,根据二次函数的性质,即可求得PQ的取值范围;
(2)首先分成两种情况讨论:当点M在上,点N在上时,可得点Q的运动区域为组成的正方形区域(不包括四个顶点);当点M在上,点N在上时,点Q的运动区域为组成的正方形区域(不包括四个顶点);综上所述,点Q的运动区域为组成的正方形区域(不包括四个顶点);然后根据直线上至少存在一个点关于的“中旋点”,可得直线与组成的正方形区域至少有一个交点(不包括顶点),当直线恰好经过时,,解得;当直线恰好经过时,,解得;结合图象可得出若直线上至少存在一个点关于的“中旋点”,则或.
8.(1)解:,
,
点为的中点,
,
当点在上运动时,,
,
由题意得:,则,
,,
,
;
当点在上运动时,,
,
由题意得:,则,
,,
,
;
综上所述,;
(2)解:画出函数图象如图所示:
,
由图象可得,函数的最大值为;
(3)
解:(3)可分成两种情况:①当当点在上运动时,,2x=,解得:x=,所以y=,即 点的距离是;② 当点在上运动时,, 2x=,解得:x=(不合题意,舍去);综上可得: 点的距离是;
故答案为:;
(1)关于的函数表达式 可分为两段来表示:① 当点在上运动时,,可得出BP=2+x, 根据含30°锐角的直角三角形的性质,可得出; ② 当点在上运动时,, 可得出CP=6-x,从而根据含30°锐角的直角三角形的性质,可得出;综上所述,可得出:;
(2)根据界点,分别描出点(0,1),(2,2)及(6,0),连接(0,1),(2,2),再连接(2,2),(6,0),即可得出函数图象,观察函数图象,可得函数的最大值为2;
(3)可分成两种情况:①当当点在上运动时,,2x=,解得:x=,所以y=,即 点的距离是;② 当点在上运动时,, 2x=,解得:x=(不合题意,舍去);综上可得: 点的距离是;
9.(1),
(2)
(3)或或
10.(1)直线的函数解析式为,直线对应的函数解析式为
(2)P的坐标为或
(3)M的坐标为或或
11.(1)直线表达式为,反比例函数的表达式为;
(2)不会改变,的面积是,的面积是.
12.(1),
(2)
(3)点坐标为或或或
13.(1)3,1
(2)
(3)
14.(1),
(2)或
(3)点的坐标为或
15.(1)
(2)
(3),,
16.(1)0或
(2)2
17.(1)
(2)
18.(1) ;(2)1
19.(1) ;(2) A(4,-2)不在这个函数图象上;(3) y1
(2)2.
21.(1)
(2)
(3)或或
22.(1)这个一次函数的解析式为
(2)
23.
24.(1)解:将,代入函数解析式得,
,
解得,
∴函数的解析式为:,
当时,得,
∴点A的坐标为.
(2)解:n的取值范围为:.
解:(2)由题意得,
,即,
又由,得,
解得,
∴的取值范围为.
(1)将点(4,3)与(-2,0)分别代入y=kx+b中,可得关于字母k、b的二元一次方程组,求解得出k、b的值,即可得到所求的函数解析式;然后令所求函数解析式中的x=0,求出对应的y的值,即可得到点A的坐标;
(2)根据题意结合解出不等式即可求解.
25.(1)设直线的解析式是,
根据题意得:,解得:,
则直线的解析式是;
(2),当时,,
,,的面积为;
设点的坐标为,,
解得或,
当时,,
当时,,
则点的坐标为或.
本题考查两条直线相交问题,用待定系数法求一次函数的解析式、坐标与图形性质以及三角形面积求法.
(1)设直线的解析式是,将点代入函数解析式可列出方程组,解方程组可求出的值,据此可求出解析式;
(2)当时,可求出点的坐标,利用三角形的面积公式求出的面积,再根据面积公式可求出点的横坐标,再代入解析式可求出点的纵坐标,据此可求出点的坐标.
26.(1)y=x-4.(2)(-4,0).
27.(1)50,
“捐款为15元”的学生有(人),补全条形统计图如下:
(2)15,15;
(3)解:样本平均数为(元/人),
∴全校八年级学生为600名,捐款总金额为(元),
答:全校八年级学生为600名,捐款总金额为8040元.
(1)解:(人),
(2)解:学生捐款金额出现次数最多的是15元,共出现18次,因此捐款金额的众数是15元,
将这50名学生捐款金额从小到大排列处在中间位置的两个数都是15元,因此中位数是15元,
故答案为:15,15.
(1)利用“A”的人数除以对应的百分比可得总人数,再求出“C”的人数并作出条形统计图即可;
(2)利用众数和中位数的定义及计算方法分析求解即可;
(3)先求出样本的平均数,再乘以总人数可得答案.
28.解:(1)设一次函数的解析式为=kx+b,
∵ 当时,当时.
∴
解得:
∴这个一次函数的解析式为:
(2))∵k=-1,∴y随x的增大而减小,
∴当y=-3时,-3=-x+5,x=8;当y=1时,1=-x+5,x=4
∴当时自变量x的取值范围是:.
(1)首先设出这个一次函数的解析式为y=kx+b(k≠0),再利用待定系数法可得方程组,再解方程组可得k、b的值,进而把得k、b的值代入解析式即可得;
(2)根据k=-1<0可得y随x的增大而减小,然后计算出y=-3时x的值,y=1时x的值,进而得到x的取值范围.
29.(1)解:∵函数y1=x+5的图象与x轴交于点A,
∴A(-5,0).
∵y=4时,x+5=4,解得x=-1,
∴D(-1,4).
将D(-1,4)代入y2=-2x+b,
得4=-2×(-1)+b,
解得b=2,
故m=-1,b=2;
(2)解:由图象可知,若y1>y2,则x的取值范围是x>-1.
故答案为x>-1;
(3)解:∵一次函数y2=-2x+2的图象分别与x轴、y轴交于点B,C,
∴B(1,0),C(0,2),
∴S四边形AOCD=S△ABD-S△BOC
=×6×4-×1×2
=12-1
=11.
(1)利用一次函数与坐标轴相交特点求得点A,D的坐标,再利用待定系数法求得b的值,即可求解;
(2)通关观察图象即可求解;
(3)先求的B,C两点的坐标,再根据S四边形AOCD=S△ABD-S△BOC代入数据计算即可求解.
30.解:作AB⊥l于B,则AB=300m,AD=500m.
∴∠ABD=90°,
在Rt△ABD中,
∴m.
设CD=AC=x,则CB=400﹣x,
x2=(400﹣x)2+3002,
x2=160000+x2﹣800x+3002,
800x=250000,
x=312.5m.
答:商店与车站之间的距离为312.5米.
作AB⊥l于B,则AB=300m,AD=500m,在Rt△ABD中,由勾股定理得BD=400m,设CD=AC=x,则CB=400﹣x,在Rt△ABC中,利用勾股定理建立方程可求出x的值,从而即可得出答案.
31.(1)证明:四边形为矩形,
,,
,
;
(2)证明:如图,连接.
,
,,
∴,
四边形是平行四边形.
平分,
,
∵,
,
,
,
四边形是菱形.
(1)由平行四边形的性质得:AB=DC,∠B=∠DCF,结合已知,用边角边可证得△ABE≌△DCF;
(2)连接DE,由(1)中的全等三角形可得AE=DF,∠AEB=∠F,由平行线的判定可得AE∥DF,根据一组对边平行且相等的四边形是平行四边形可得四边形AEFD是平行四边形,由角平分线的定义和平行线的性质可得∠ADE=∠AED,由等角对等边可得AE=AD,根据有一组邻边相等的平行四边形是菱形可求解.
32.(1),
(2)当时,四边形是平行四边形;,
(3)或;,,或,
33.绿地的面积为96
34.(1)
(2)y的值为
35.(1)
(2)①;②
36.(1)解:.
∵函数为正比例函数,
∴,
解得:,
答:当时,这个函数为正比例函数
(2)解:一次函数.
∵函数y的值随着x值的增大而减小,
∴,
答:当时,函数y的值随着x值的增大而减小.
(1)根据正比例函数的定义,即可得出,解方程即可得出m的值;
(2)根据一次函数的性质,即可得出m<0.
37.(1)解:,
∴,
∴,,
(2)解:∵,,,
∴,
∵,
∴长为a,b,c的三条线段不能构成直角三角形.
(1)根据偶次方的非负性、绝对值的非负性、算术平方根的非负性,且这三个非负项之和为0,所以每一项都必须等于0,分别建立方程求解即可;
(2)分别计算,进而根据勾股定理的逆定理进行判断,即可求解.
38.(1)解:∵米,米
∴根据勾股定理可得(米),
由题可知,米,
∴米;
(2)解:根据勾股定理可得:放出后(米),
即他应该放出8米.
(1)先利用勾股定理求出AC的长,再利用线段的和差求出AD的长即可;
(2)先利用勾股定理求出AB的长,再列出算式求解即可.
39.(1);(2),;(3),.
40.(1)运动时间时的面积为
(2)或或或时,为等腰三角形
41.(1)
(2)①的长为2;②
同课章节目录
