期中真题专项复习01选择题(含解析)--2024-2025学年八年级数学下册(人教版)
文档属性
| 名称 | 期中真题专项复习01选择题(含解析)--2024-2025学年八年级数学下册(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 529.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 13:25:27 | ||
图片预览


文档简介
2024-2025学年八年级数学下册(人教版)
期中真题专项复习01选择题
一、选择题
1.(2023八下·恩平期中)如图,在平行四边形ABCD中,∠ABC=78°,AE⊥BC于点E,AE交BD于点F,若DF=2AB,则∠AFD的大小是( )
A.62° B.64° C.66° D.68°
2.(2024八下·江陵期中)下列计算正确的是( )
A. B. C. D.
3.(2023八下·番禺期中)如图,四边形中,对角线、相交于点,下列条件不能判定这个四边形是平行四边形的是( )
A., B.,
C., D.,
4.(2024八下·民勤期中)实数在数轴上的位置如图所示,则化简后为( )
A. B. C. D.无法确定
5.(2024八下·庄浪期中)如图,圆柱形容器的底面周长是,高是,在外侧地面S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处的点F处有一苍蝇,急于捕捉苍蝇充饥的蜘蛛所走的最短路线长度是( ).
A.18 B.20 C.22 D.24
6.(2024八下·开州期中)如图,在平行四边形中,于⊥于F,相交于与的延长线相交于点G,下面给出四个结论:①;②;③;④,其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
7.(2024八下·福州期中)一次函数与的图象如图所示,则下列结论:
①,②;③随的增大而增大;④当时,;⑤;其中正确的个数是( )
A.个 B.个 C.个 D.个
8.(2024八下·城厢期中)对于一次函数,下列结论正确的是( )
A.函数值y随自变量x的增大而减小
B.函数图象与y轴的交点坐标是
C.函数图象与x轴的正方向成角
D.函数图象不经过第四象限
9.(2024八下·武鸣期中)小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈,小臂水平转向两侧,两手将绳拉直,绳长即合适长度.将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1.2米,则适合小华的绳长为( )
A.2.2米 B.2.4米 C.2.6米 D.2.8米
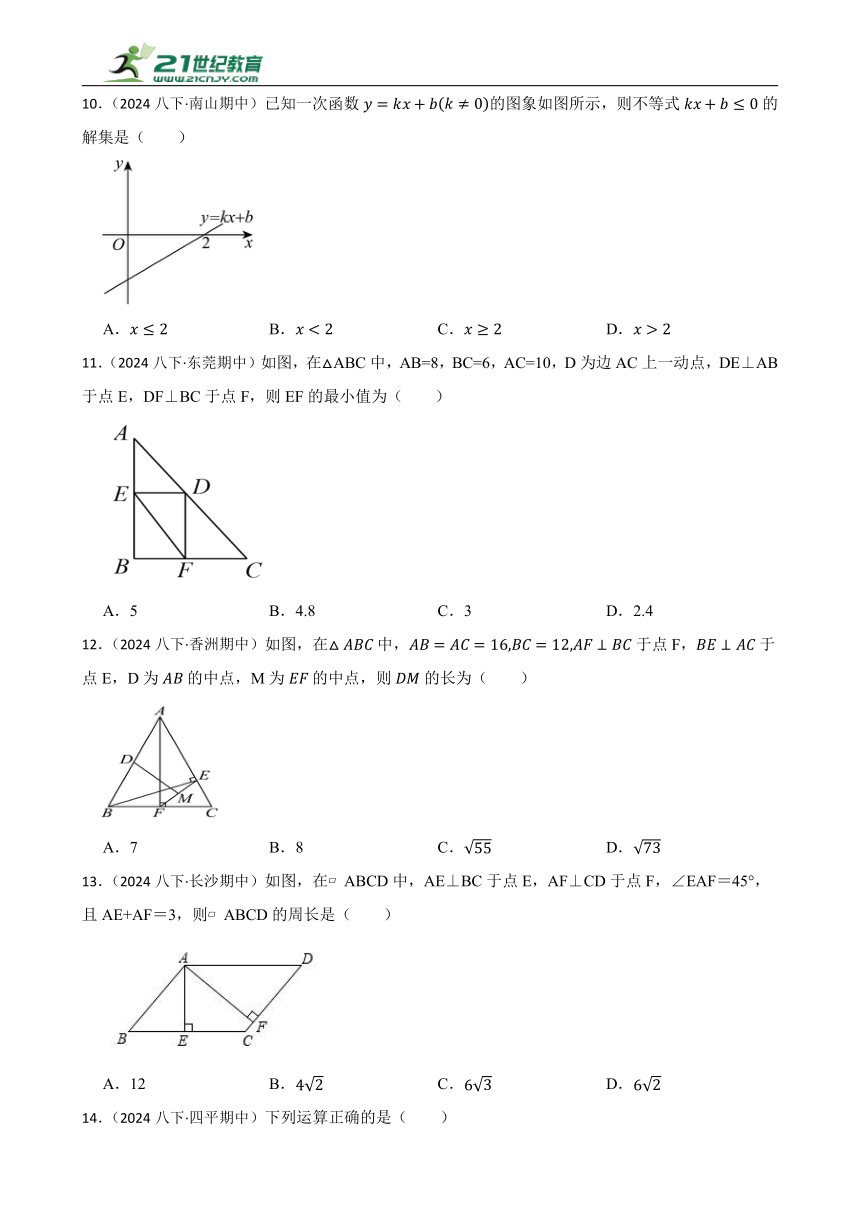
10.(2024八下·南山期中)已知一次函数的图象如图所示,则不等式的解集是( )
A. B. C. D.
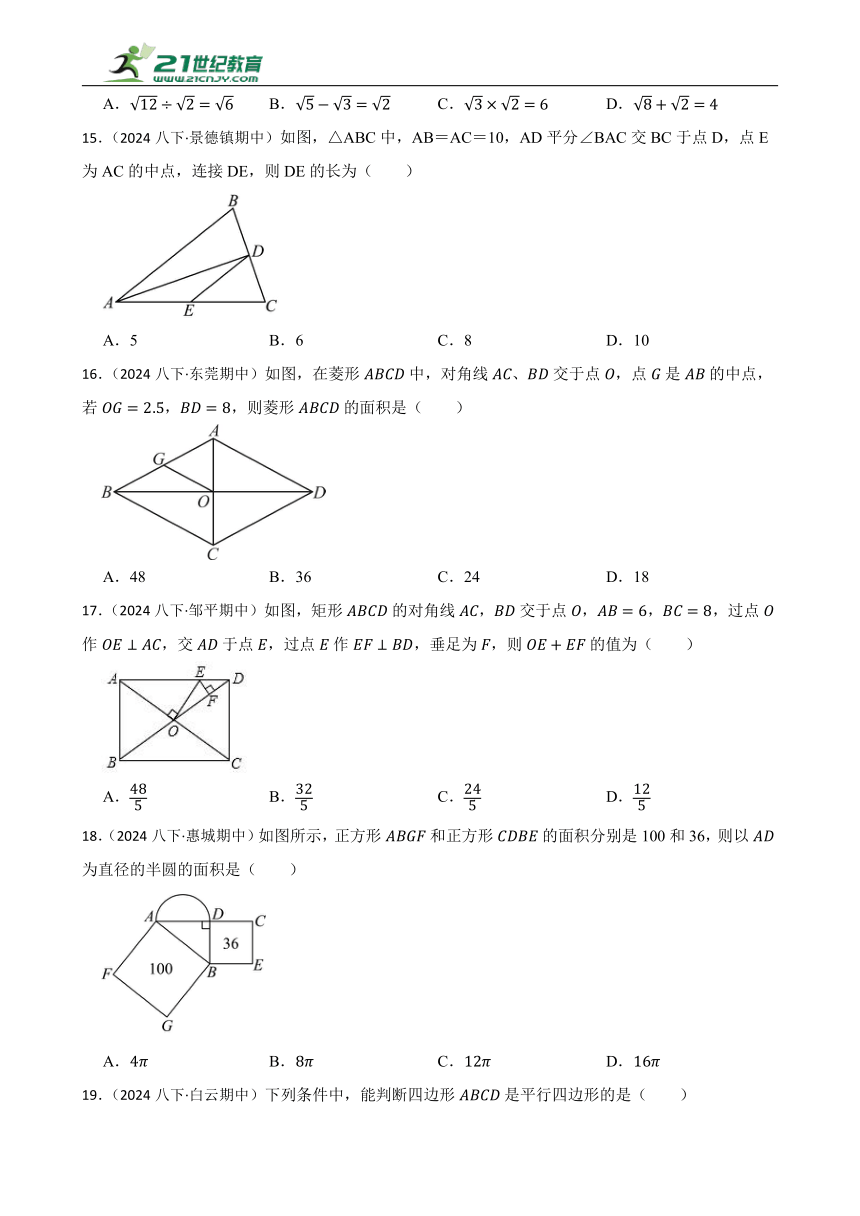
11.(2024八下·东莞期中)如图,在ABC中,AB=8,BC=6,AC=10,D为边AC上一动点,DE⊥AB于点E,DF⊥BC于点F,则EF的最小值为( )
A.5 B.4.8 C.3 D.2.4
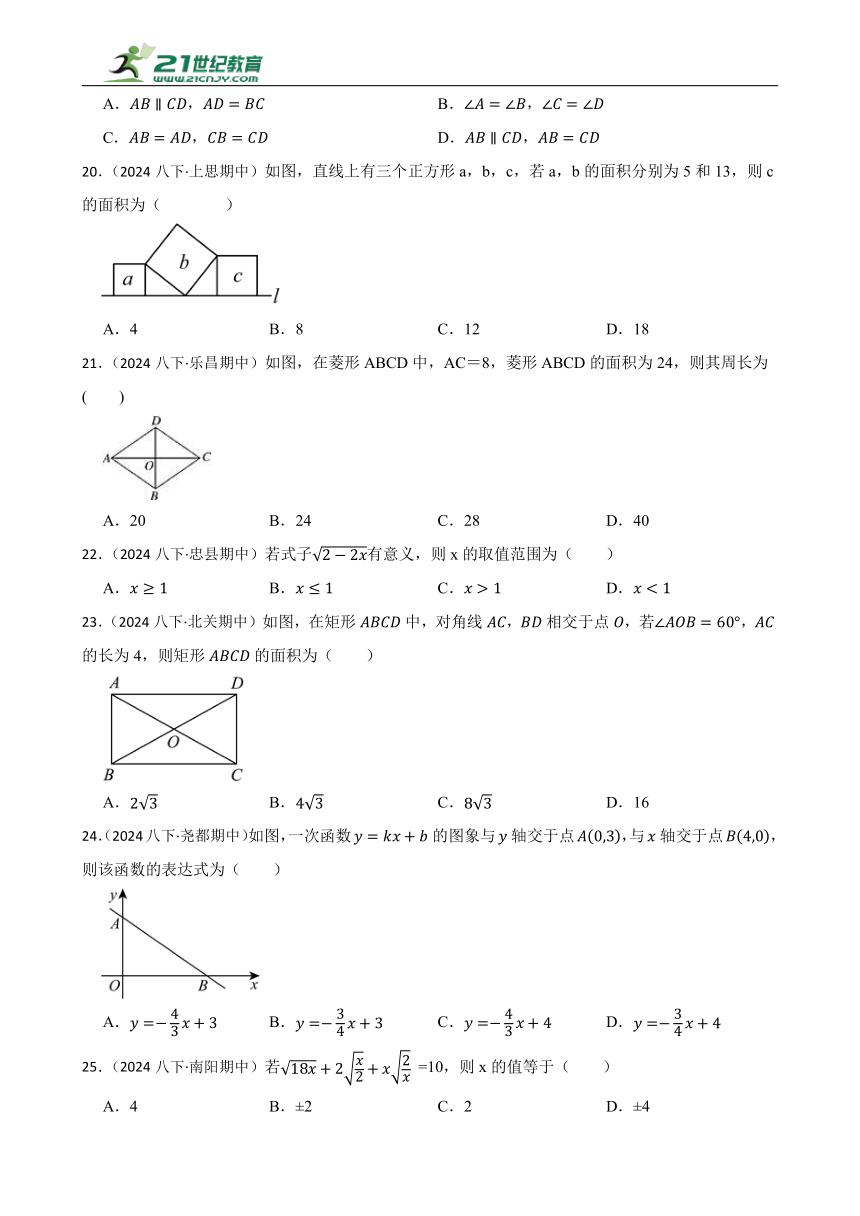
12.(2024八下·香洲期中)如图,在中,于点F,于点E,D为的中点,M为的中点,则的长为( )
A.7 B.8 C. D.
13.(2024八下·长沙期中)如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,∠EAF=45°,且AE+AF=3,则 ABCD的周长是( )
A.12 B. C. D.
14.(2024八下·四平期中)下列运算正确的是( )
A. B. C. D.
15.(2024八下·景德镇期中)如图,△ABC中,AB=AC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则DE的长为( )
A.5 B.6 C.8 D.10
16.(2024八下·东莞期中)如图,在菱形中,对角线、交于点,点是的中点,若,,则菱形的面积是( )
A.48 B.36 C.24 D.18
17.(2024八下·邹平期中)如图,矩形的对角线,交于点,,,过点作,交于点,过点作,垂足为,则的值为( )
A. B. C. D.
18.(2024八下·惠城期中)如图所示,正方形和正方形的面积分别是100和36,则以为直径的半圆的面积是( )
A. B. C. D.
19.(2024八下·白云期中)下列条件中,能判断四边形是平行四边形的是( )
A., B.,
C., D.,
20.(2024八下·上思期中)如图,直线上有三个正方形a,b,c,若a,b的面积分别为5和13,则c的面积为( )
A.4 B.8 C.12 D.18
21.(2024八下·乐昌期中)如图,在菱形ABCD中,AC=8,菱形ABCD的面积为24,则其周长为( )
A.20 B.24 C.28 D.40
22.(2024八下·忠县期中)若式子有意义,则x的取值范围为( )
A. B. C. D.
23.(2024八下·北关期中)如图,在矩形中,对角线,相交于点,若,的长为4,则矩形的面积为( )
A. B. C. D.16
24.(2024八下·尧都期中)如图,一次函数的图象与轴交于点,与轴交于点,则该函数的表达式为( )
A. B. C. D.
25.(2024八下·南阳期中)若 =10,则x的值等于( )
A.4 B.±2 C.2 D.±4
26.(2024八下·奉化期中)如图,是三角形的中位线,平分,且,若,,则的长为( )
A.4 B.3 C.2 D.1
27.(2023八下·新兴期中)下列长度的三条线段不能构成直角三角形的是( )
A.,, B.,,
C. D.,,
28.(2024八下·涧西期中)如图,四边形的对角线交于点,下列能判断四边形是平行四边形的是( )
A., B.,
C., D.,
29.(2023八下·东莞期中)若二次根式在实数范围内有意义,则的取值范围是( )
A. B. C. D.
30.(2024八下·天津市期中)如图,和都是等腰直角三角形,的顶点A在的斜边上,下列结论:①;②;③;④;⑤.其中正确的有( )
A.2个 B.3个 C.4个 D.5 个
31.(2024八下·天津市期中)如图,钓鱼竿的长为m,露在水面上的鱼线长为m.钓鱼者想看鱼钩上的情况,把钓鱼竿转到的位置,此时露在水面上的鱼线长为m,则的长为( )
A.m B.m C.m D.m
32.(2024八下·攀枝花期中)如图,一次函数y=ax+b的图像交x轴于点(2,0),交y轴与点(0,4),则下面说法正确的是( )
A.关于x的不等式ax+b>0的解集是x>2
B.关于x的不等式ax+b<0的解集是x<2
C.关于x的方程ax+b=0的解是x=4
D.关于x的方程ax+b=0的解是x=2
33.(2023八下·南海期中)如图,已知直线过点,过点的直线交轴于点,则关于的不等式组的解集为( )
A. B. C. D.
34.(2024八下·淄博期中)如图,在正方形中,F是边上的一点,连结并延长与的延长线相交于点E.若,则的值为( )
A. B. C. D.
35.(2024八下·开封期中)函数中自变量x的取值范围是( )
A.且 B.
C. D.且
36.(2024八下·广州期中)如图,菱形中,对角线与相交于点O,E为的中点,若,则的长为( )
A.5cm B.4cm C.3cm D.cm
37.(2020八下·北京期中)下列长度的三条线段,能成为一个直角三角形的三边的一组是( )
A. B.1,2, C.2,4, D.9,16,25
38.(2024八下·唐山期中)如图,在平行四边形ABCD中,E、F、G、H分别是各边的中点,在下列四个图形中,阴影部分的面积与其他三个阴影部分面积不相等的是( )
A. B.
C. D.
39.(2024八下·钱塘期中)数据0,1,2的方差是( )
A. B. C.1 D.2
40.(2024八下·旌阳期中)如图,的对角线,相交于点O,的平分线与边相交于点P,E是中点,若,,则的长为( )
A.1 B.2 C.3 D.4
41.(2024八下·厦门期中)如图,,分别为边上的点.要使,需添加一个条件,下列添加条件不正确的是( )
A. B. C. D.
42.(2024八下·厦门期中)在中,若,则下列说法正确的是( )
A.是锐角三角形 B.是直角三角形且
C.是直角三角形且 D.是钝角三角形
43.(2024八下·南京期中)下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.矩形是轴对称图形,两条对角线所在的直线是它的对称轴
D.对角线互相垂直的平行四边形为菱形
44.(2024八下·承德期中)如图,矩形的对角线、相交于点O,分别过点C、D作、的平行线相交于点E.若,则点E到的距离是( )
A.7 B.8 C.9 D.12
45.(2024八下·新沂期中)下列命题是真命题的是( )
A.矩形的对角线互相垂直
B.菱形的对角线相等
C.对角线互相平分的四边形是平行四边形
D.四个角都相等的四边形是正方形
46.(2024八下·福建期中)一组数据2、3,7、7、5,则这组数据的众数为( )
A.2 B.3 C.5 D.7
47.(2024八下·聊城期中)如图,是内一点,,,,,、、、分别是、、、的中点,则四边形的周长是( )
A.11 B.10 C.9 D.8
48.(2024八下·任城期中)如图,在中,,D为中点,若,则的长是( )
A.6 B.5 C.4 D.3
49.(2019八下·闽侯期中)一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
50.(2024八下·保山期中)下列运算中,正确的是( )
A.÷=2 B.=±5 C.5 =5 D. =
答案解析部分
1.B
解:取DF的中点H,连接AH,如下图:
∵AE⊥BC,∠ABC=78°,四边形ABCD是平行四边形
∴∠EAD=90°,AD∥BC
∴∠BAE=12°,∠CBD=∠ADB
∵点H为DF的中点
∴AH=DH=FH=DF=AB
∴∠ABH=∠AHB,∠AHD=∠HAD,∠HAF=∠HFA
∵∠AHB=∠HAD+∠HDA=2∠HDA
∴∠ABH=2∠HDA=2∠CBD,∠CBD+∠ABD=∠ABC=78°
∴∠CBD=26°=∠ADH
∴∠AFD=90°-26°=64°
故答案为:B.
根据直角三角形的性质,可得AB=AH=DH=FH,进而可得∠ABH=∠AHB,∠ADH=∠HAD,∠HAF=∠HFA;根据三角形外角性质,可得∠CBD=26°=∠ADH,即可求解.
2.C
A、 与 不是同类二次根式,不可合并,此项不符合题意;
B、 ,此项不符合题意;
C、 ,此项符合题意;
D、 ,此项不符合题意;
故答案为:C.
利用二次根式的加减法则,乘法法则和除法法则,对每个选项一一判断求解即可。
3.B
解:
A、由“AB∥DC,AD∥BC"可知,四边形ABCD的两组对边互相平行,则该四边形是平行四边形,故选项A不符合题意;
B、由“AB∥DC,AD=BC"可知,四边形ABCD的一组对边相等,另一组对边平行,所以四边形可能是平行四边形,也可能是等腰梯形,所以不能判定该四边形是平行四边形,故选项B符合题意;
C、由“AO=CO,BO=DO”可知,四边形ABCD的两条对角线互相平分,则该四边形是平行四边形,故选项C不符合题意;
D、由“AB=DC,AD=BC”可知四边形ABCD的两组对边相等,则该四边形是平行四边形,故选项B不符合题意,
故答案为:B.
本题考查平行四边的判定定理,根据判定定理逐项判断即可.
4.A
5.B
6.B
7.D
解:∵一次函数的图象经过第二、四象限,
∴,故①正确;
∵一次函数与y轴交于正半轴,
∴,
∵一次函数的图象与轴的交点位于轴的负半轴上,
∴,
∴,故②正确;
∵一次函数中,,
∴随的增大而减小,故③错误;
当时,一次函数的图象在一次函数的图象上方,
∴当时,,故④正确;
∵一次函数与的图象的交点的横坐标为,
∴当时,,
∴,故⑤正确;
综上所述,其中正确的有个.
故答案为:.
①根据函数图象,确定k的符号;
②根据函数图象,确定b的符号,再根据一次函数的图象与轴的交点,确定a的符号,再确定ab的符号;
③由①中得出的k的符号来说明增减性;
④根据两直线的交点的横坐标及两直线的位置,来确定时函数值的大小;
⑤根据两直线的交点的横坐标,可知两个函数值相等.
8.A
9.C
解:作于,
,
由题意可得:,,,
,
,
,
,
适合小华的绳长为2.6米,
故选:C.
作于,由题意可得:,,,由等腰三角形的性质可得,由勾股定理可得,则,即适合小华的绳长为2.6米.
10.A
解:由图象可得:当时,,
∴不等式的解集为,
故选:A.
通过观察函数图象,确定当函数值小于等于0时,自变量x的取值范围。这个范围就是不等式的解集。
11.B
解:如图,连接BD,
∵在△ABC中,AB=8,BC=6,AC=10,
∴AB2+BC2=AC2,即∠ABC=90°.
∵DE⊥AB于点E,DF⊥BC于点F,
∴四边形EDFB是矩形,
∴EF=BD.
∵BD的最小值即为直角三角形ABC斜边上的高,即4.8,
∴EF的最小值为4.8,
故答案为:B.
连接BD,先证出四边形EDFB是矩形,再结合BD的最小值即为直角三角形ABC斜边上的高,即4.8,即可得到EF的最小值为4.8.
12.C
解:连接,
∵,
∴F是中点,
∵,
∴,
∴,
同理:,
∴,
∵M为的中点,
∴,
∴.
故答案为:C.
连接,根据等腰三角形三线合一得到F是中点,从而得到,同理可得,最后根据勾股定理即可求出的长.
13.D
解:∵∠EAF=45°,
∴∠C=360°﹣∠AEC﹣∠AFC﹣∠EAF=135°,
∴∠B=∠D=180°﹣∠C=45°,
则AE=BE,AF=DF,
设AE=x,则AF=3﹣x,
在Rt△ABE中,
根据勾股定理可得,AB=x
同理可得AD=(3﹣x)
则平行四边形ABCD的周长是2(AB+AD)=2[x+(3﹣x)]=6,
故答案为:D.
根据角之间的数量关系得到:AE=BE,AF=DF,设AE=x,则AF=3﹣x,然后利用勾股定理计算即可求解.
14.A
15.A
16.C
解:∵菱形,
∴,,,
∵,,
∴,,
∴,
∴,
∴菱形的面积是.
故选:C.
根据菱形的性质和已知条件可得OG是斜边上的中线,进而可求出AB的长,再根据勾股定理可求出OA的长,最后根据菱形的面积等于对角线乘积的一半计算即可.
17.C
解:∵四边形ABCD是矩形,
,
,
,
,,
,
,
,
又,
,
,
,
,,
,
同理可证,,
,
,
,
,
故答案为:C.
根据勾股定理求出AC=BD=10,由矩形的性质得出AO=5,证明得到OE的长,再证明可得到EF的长,从而可得到结论.
18.B
由题意可得,BD=6,AB=10,
则在直角三角形ABC中,AD=8,
则以AD为直径的半圆的面积为:.
故选:B
先根据两个正方形的面积求得边长AB与BD的长度,然后根据勾股定理求得直角三角形中AD的长度,最后根据圆的面积公式求得半圆的面积.
19.D
20.B
21.A
22.B
解:要使二次根式有意义,
只需使:,
解得:,
故答案为:B.
根据二次根式有意义的条件“被开方数非负”可得关于x的不等式,解不等式可求解.
23.B
解:∵四边形是矩形,
,
,
是等边三角形,
,
在中,,
∴,
,
矩形的面积是,
故选:B.
根据矩形的性质及已知可推出是等边三角形,可得,利用三角形内角和求出,根据含30度角的直角三角形的性质以及勾股定理求得,根据矩形的面积=AB×BC进行计算即可.
24.B
解:∵一次函数的图象与轴交于点,与轴交于点,
解得
∴该函数的表达式为
故选:B.
本题考查待定系数法求一次函数的解析式.根据一次函数的图象与轴交于点,与轴交于点,将点A和点B代入函数解析式可列出方程组,解方程组可求出k和b的值,据此可求出函数解析式.
25.C
解:3 + + =10,
5 =10,
=2,
则2x=4,
x=2,
故答案为:C
由二次根式的性质“、、”可将方程左边化简得:3 + + =10,再合并同类二次根式得,5 =10,把方程两边同时平方可去掉根号,然后按照一元一次方程的解题步骤计算即可求解。
26.C
27.C
解:A、,
由长度为6、8、10的三条线段能构成直角三角形,故此选项不符合题意;
B、,
由长度为0.3、0.4、0.5的三条线段能构成直角三角形,故此选项不符合题意;
C、,
由长度为、、的三条线段不能构成直角三角形,故此选项符合题意;
D、,
由长度为1、、的三条线段能构成直角三角形,故此选项不符合题意.
故答案为:C.
根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形,据此逐一判断得出答案.
28.C
解:根据,,不能判定四边形是平行四边形,故A不符合题意;
根据,,不能判定四边形是平行四边形,故B不符合题意;
,
,,
,
,
四边形是平行四边形,故C符合题意;
根据,,不能判定四边形是平行四边形,故D不符合题意;
故选:C.
根据平行四边形的判定方法对各个选项逐一进行判断.
29.A
30.C
31.A
解∶ 在中,m,m,
根据勾股定理得, m
在中,m,m,
根据勾股定理得, m,
∴ m,
故答案为∶A.
根据勾股定理进行计算即可求出答案.
32.D
33.D
34.B
35.D
36.D
37.B
解:A、∵( )2+( )2≠( )2,∴不能构成直角三角形,故本选项不符合题意;
B、∵12+( )2=22,∴能构成直角三角形,故本选项符合题意;
C、∵22+( )2≠42,∴不能构成直角三角形,故本选项不符合题意;
D、∵92+162≠252,∴不能构成直角三角形,故本选项不符合题意.
故答案为:B.
根据勾股定理的逆定理逐项判定即可。
38.B
39.B
解:平均数==1,
∴ 方差==.
故答案为:B.
先求出平均数,再根据方差的定义,即可求得.
40.A
41.D
42.C
43.D
44.C
45.C
46.D
因为7出现了2次,其他数据都是出现了1次,
所以7出现的次数最多,
所以这组数据中众数是7.
故选:D.
众数是一组数据中出现次数最多的数.
47.A
48.C
49.B
解:根据题意,一次函数y=kx+b的值随x的增大而增大,即k>0,
又∵b<0,
∴这个函数的图象经过第一三四象限,
∴不经过第二象限,
故答案为:B.
根据题意,一次函数y=kx+b的值随x的增大而增大,即k>0,又因为b<0所以,这个函数的图象经过第一三四象限,不经过第二象限.
50.A
解:A、,故A符合题意;
B、,故B不符合题意;
C、,故C不符合题意;
D、不能计算,故D不符合题意;
故答案为:A
利用二次根式的除法法则进行计算,可对A作出判断;利用二次根式的性质,可对B作出判断利用同类二次根式的定义和合并同类二次根式的法则,可对D,C作出判断.
期中真题专项复习01选择题
一、选择题
1.(2023八下·恩平期中)如图,在平行四边形ABCD中,∠ABC=78°,AE⊥BC于点E,AE交BD于点F,若DF=2AB,则∠AFD的大小是( )
A.62° B.64° C.66° D.68°
2.(2024八下·江陵期中)下列计算正确的是( )
A. B. C. D.
3.(2023八下·番禺期中)如图,四边形中,对角线、相交于点,下列条件不能判定这个四边形是平行四边形的是( )
A., B.,
C., D.,
4.(2024八下·民勤期中)实数在数轴上的位置如图所示,则化简后为( )
A. B. C. D.无法确定
5.(2024八下·庄浪期中)如图,圆柱形容器的底面周长是,高是,在外侧地面S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口内侧距开口处的点F处有一苍蝇,急于捕捉苍蝇充饥的蜘蛛所走的最短路线长度是( ).
A.18 B.20 C.22 D.24
6.(2024八下·开州期中)如图,在平行四边形中,于⊥于F,相交于与的延长线相交于点G,下面给出四个结论:①;②;③;④,其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
7.(2024八下·福州期中)一次函数与的图象如图所示,则下列结论:
①,②;③随的增大而增大;④当时,;⑤;其中正确的个数是( )
A.个 B.个 C.个 D.个
8.(2024八下·城厢期中)对于一次函数,下列结论正确的是( )
A.函数值y随自变量x的增大而减小
B.函数图象与y轴的交点坐标是
C.函数图象与x轴的正方向成角
D.函数图象不经过第四象限
9.(2024八下·武鸣期中)小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈,小臂水平转向两侧,两手将绳拉直,绳长即合适长度.将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1.2米,则适合小华的绳长为( )
A.2.2米 B.2.4米 C.2.6米 D.2.8米
10.(2024八下·南山期中)已知一次函数的图象如图所示,则不等式的解集是( )
A. B. C. D.
11.(2024八下·东莞期中)如图,在ABC中,AB=8,BC=6,AC=10,D为边AC上一动点,DE⊥AB于点E,DF⊥BC于点F,则EF的最小值为( )
A.5 B.4.8 C.3 D.2.4
12.(2024八下·香洲期中)如图,在中,于点F,于点E,D为的中点,M为的中点,则的长为( )
A.7 B.8 C. D.
13.(2024八下·长沙期中)如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,∠EAF=45°,且AE+AF=3,则 ABCD的周长是( )
A.12 B. C. D.
14.(2024八下·四平期中)下列运算正确的是( )
A. B. C. D.
15.(2024八下·景德镇期中)如图,△ABC中,AB=AC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则DE的长为( )
A.5 B.6 C.8 D.10
16.(2024八下·东莞期中)如图,在菱形中,对角线、交于点,点是的中点,若,,则菱形的面积是( )
A.48 B.36 C.24 D.18
17.(2024八下·邹平期中)如图,矩形的对角线,交于点,,,过点作,交于点,过点作,垂足为,则的值为( )
A. B. C. D.
18.(2024八下·惠城期中)如图所示,正方形和正方形的面积分别是100和36,则以为直径的半圆的面积是( )
A. B. C. D.
19.(2024八下·白云期中)下列条件中,能判断四边形是平行四边形的是( )
A., B.,
C., D.,
20.(2024八下·上思期中)如图,直线上有三个正方形a,b,c,若a,b的面积分别为5和13,则c的面积为( )
A.4 B.8 C.12 D.18
21.(2024八下·乐昌期中)如图,在菱形ABCD中,AC=8,菱形ABCD的面积为24,则其周长为( )
A.20 B.24 C.28 D.40
22.(2024八下·忠县期中)若式子有意义,则x的取值范围为( )
A. B. C. D.
23.(2024八下·北关期中)如图,在矩形中,对角线,相交于点,若,的长为4,则矩形的面积为( )
A. B. C. D.16
24.(2024八下·尧都期中)如图,一次函数的图象与轴交于点,与轴交于点,则该函数的表达式为( )
A. B. C. D.
25.(2024八下·南阳期中)若 =10,则x的值等于( )
A.4 B.±2 C.2 D.±4
26.(2024八下·奉化期中)如图,是三角形的中位线,平分,且,若,,则的长为( )
A.4 B.3 C.2 D.1
27.(2023八下·新兴期中)下列长度的三条线段不能构成直角三角形的是( )
A.,, B.,,
C. D.,,
28.(2024八下·涧西期中)如图,四边形的对角线交于点,下列能判断四边形是平行四边形的是( )
A., B.,
C., D.,
29.(2023八下·东莞期中)若二次根式在实数范围内有意义,则的取值范围是( )
A. B. C. D.
30.(2024八下·天津市期中)如图,和都是等腰直角三角形,的顶点A在的斜边上,下列结论:①;②;③;④;⑤.其中正确的有( )
A.2个 B.3个 C.4个 D.5 个
31.(2024八下·天津市期中)如图,钓鱼竿的长为m,露在水面上的鱼线长为m.钓鱼者想看鱼钩上的情况,把钓鱼竿转到的位置,此时露在水面上的鱼线长为m,则的长为( )
A.m B.m C.m D.m
32.(2024八下·攀枝花期中)如图,一次函数y=ax+b的图像交x轴于点(2,0),交y轴与点(0,4),则下面说法正确的是( )
A.关于x的不等式ax+b>0的解集是x>2
B.关于x的不等式ax+b<0的解集是x<2
C.关于x的方程ax+b=0的解是x=4
D.关于x的方程ax+b=0的解是x=2
33.(2023八下·南海期中)如图,已知直线过点,过点的直线交轴于点,则关于的不等式组的解集为( )
A. B. C. D.
34.(2024八下·淄博期中)如图,在正方形中,F是边上的一点,连结并延长与的延长线相交于点E.若,则的值为( )
A. B. C. D.
35.(2024八下·开封期中)函数中自变量x的取值范围是( )
A.且 B.
C. D.且
36.(2024八下·广州期中)如图,菱形中,对角线与相交于点O,E为的中点,若,则的长为( )
A.5cm B.4cm C.3cm D.cm
37.(2020八下·北京期中)下列长度的三条线段,能成为一个直角三角形的三边的一组是( )
A. B.1,2, C.2,4, D.9,16,25
38.(2024八下·唐山期中)如图,在平行四边形ABCD中,E、F、G、H分别是各边的中点,在下列四个图形中,阴影部分的面积与其他三个阴影部分面积不相等的是( )
A. B.
C. D.
39.(2024八下·钱塘期中)数据0,1,2的方差是( )
A. B. C.1 D.2
40.(2024八下·旌阳期中)如图,的对角线,相交于点O,的平分线与边相交于点P,E是中点,若,,则的长为( )
A.1 B.2 C.3 D.4
41.(2024八下·厦门期中)如图,,分别为边上的点.要使,需添加一个条件,下列添加条件不正确的是( )
A. B. C. D.
42.(2024八下·厦门期中)在中,若,则下列说法正确的是( )
A.是锐角三角形 B.是直角三角形且
C.是直角三角形且 D.是钝角三角形
43.(2024八下·南京期中)下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.矩形是轴对称图形,两条对角线所在的直线是它的对称轴
D.对角线互相垂直的平行四边形为菱形
44.(2024八下·承德期中)如图,矩形的对角线、相交于点O,分别过点C、D作、的平行线相交于点E.若,则点E到的距离是( )
A.7 B.8 C.9 D.12
45.(2024八下·新沂期中)下列命题是真命题的是( )
A.矩形的对角线互相垂直
B.菱形的对角线相等
C.对角线互相平分的四边形是平行四边形
D.四个角都相等的四边形是正方形
46.(2024八下·福建期中)一组数据2、3,7、7、5,则这组数据的众数为( )
A.2 B.3 C.5 D.7
47.(2024八下·聊城期中)如图,是内一点,,,,,、、、分别是、、、的中点,则四边形的周长是( )
A.11 B.10 C.9 D.8
48.(2024八下·任城期中)如图,在中,,D为中点,若,则的长是( )
A.6 B.5 C.4 D.3
49.(2019八下·闽侯期中)一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
50.(2024八下·保山期中)下列运算中,正确的是( )
A.÷=2 B.=±5 C.5 =5 D. =
答案解析部分
1.B
解:取DF的中点H,连接AH,如下图:
∵AE⊥BC,∠ABC=78°,四边形ABCD是平行四边形
∴∠EAD=90°,AD∥BC
∴∠BAE=12°,∠CBD=∠ADB
∵点H为DF的中点
∴AH=DH=FH=DF=AB
∴∠ABH=∠AHB,∠AHD=∠HAD,∠HAF=∠HFA
∵∠AHB=∠HAD+∠HDA=2∠HDA
∴∠ABH=2∠HDA=2∠CBD,∠CBD+∠ABD=∠ABC=78°
∴∠CBD=26°=∠ADH
∴∠AFD=90°-26°=64°
故答案为:B.
根据直角三角形的性质,可得AB=AH=DH=FH,进而可得∠ABH=∠AHB,∠ADH=∠HAD,∠HAF=∠HFA;根据三角形外角性质,可得∠CBD=26°=∠ADH,即可求解.
2.C
A、 与 不是同类二次根式,不可合并,此项不符合题意;
B、 ,此项不符合题意;
C、 ,此项符合题意;
D、 ,此项不符合题意;
故答案为:C.
利用二次根式的加减法则,乘法法则和除法法则,对每个选项一一判断求解即可。
3.B
解:
A、由“AB∥DC,AD∥BC"可知,四边形ABCD的两组对边互相平行,则该四边形是平行四边形,故选项A不符合题意;
B、由“AB∥DC,AD=BC"可知,四边形ABCD的一组对边相等,另一组对边平行,所以四边形可能是平行四边形,也可能是等腰梯形,所以不能判定该四边形是平行四边形,故选项B符合题意;
C、由“AO=CO,BO=DO”可知,四边形ABCD的两条对角线互相平分,则该四边形是平行四边形,故选项C不符合题意;
D、由“AB=DC,AD=BC”可知四边形ABCD的两组对边相等,则该四边形是平行四边形,故选项B不符合题意,
故答案为:B.
本题考查平行四边的判定定理,根据判定定理逐项判断即可.
4.A
5.B
6.B
7.D
解:∵一次函数的图象经过第二、四象限,
∴,故①正确;
∵一次函数与y轴交于正半轴,
∴,
∵一次函数的图象与轴的交点位于轴的负半轴上,
∴,
∴,故②正确;
∵一次函数中,,
∴随的增大而减小,故③错误;
当时,一次函数的图象在一次函数的图象上方,
∴当时,,故④正确;
∵一次函数与的图象的交点的横坐标为,
∴当时,,
∴,故⑤正确;
综上所述,其中正确的有个.
故答案为:.
①根据函数图象,确定k的符号;
②根据函数图象,确定b的符号,再根据一次函数的图象与轴的交点,确定a的符号,再确定ab的符号;
③由①中得出的k的符号来说明增减性;
④根据两直线的交点的横坐标及两直线的位置,来确定时函数值的大小;
⑤根据两直线的交点的横坐标,可知两个函数值相等.
8.A
9.C
解:作于,
,
由题意可得:,,,
,
,
,
,
适合小华的绳长为2.6米,
故选:C.
作于,由题意可得:,,,由等腰三角形的性质可得,由勾股定理可得,则,即适合小华的绳长为2.6米.
10.A
解:由图象可得:当时,,
∴不等式的解集为,
故选:A.
通过观察函数图象,确定当函数值小于等于0时,自变量x的取值范围。这个范围就是不等式的解集。
11.B
解:如图,连接BD,
∵在△ABC中,AB=8,BC=6,AC=10,
∴AB2+BC2=AC2,即∠ABC=90°.
∵DE⊥AB于点E,DF⊥BC于点F,
∴四边形EDFB是矩形,
∴EF=BD.
∵BD的最小值即为直角三角形ABC斜边上的高,即4.8,
∴EF的最小值为4.8,
故答案为:B.
连接BD,先证出四边形EDFB是矩形,再结合BD的最小值即为直角三角形ABC斜边上的高,即4.8,即可得到EF的最小值为4.8.
12.C
解:连接,
∵,
∴F是中点,
∵,
∴,
∴,
同理:,
∴,
∵M为的中点,
∴,
∴.
故答案为:C.
连接,根据等腰三角形三线合一得到F是中点,从而得到,同理可得,最后根据勾股定理即可求出的长.
13.D
解:∵∠EAF=45°,
∴∠C=360°﹣∠AEC﹣∠AFC﹣∠EAF=135°,
∴∠B=∠D=180°﹣∠C=45°,
则AE=BE,AF=DF,
设AE=x,则AF=3﹣x,
在Rt△ABE中,
根据勾股定理可得,AB=x
同理可得AD=(3﹣x)
则平行四边形ABCD的周长是2(AB+AD)=2[x+(3﹣x)]=6,
故答案为:D.
根据角之间的数量关系得到:AE=BE,AF=DF,设AE=x,则AF=3﹣x,然后利用勾股定理计算即可求解.
14.A
15.A
16.C
解:∵菱形,
∴,,,
∵,,
∴,,
∴,
∴,
∴菱形的面积是.
故选:C.
根据菱形的性质和已知条件可得OG是斜边上的中线,进而可求出AB的长,再根据勾股定理可求出OA的长,最后根据菱形的面积等于对角线乘积的一半计算即可.
17.C
解:∵四边形ABCD是矩形,
,
,
,
,,
,
,
,
又,
,
,
,
,,
,
同理可证,,
,
,
,
,
故答案为:C.
根据勾股定理求出AC=BD=10,由矩形的性质得出AO=5,证明得到OE的长,再证明可得到EF的长,从而可得到结论.
18.B
由题意可得,BD=6,AB=10,
则在直角三角形ABC中,AD=8,
则以AD为直径的半圆的面积为:.
故选:B
先根据两个正方形的面积求得边长AB与BD的长度,然后根据勾股定理求得直角三角形中AD的长度,最后根据圆的面积公式求得半圆的面积.
19.D
20.B
21.A
22.B
解:要使二次根式有意义,
只需使:,
解得:,
故答案为:B.
根据二次根式有意义的条件“被开方数非负”可得关于x的不等式,解不等式可求解.
23.B
解:∵四边形是矩形,
,
,
是等边三角形,
,
在中,,
∴,
,
矩形的面积是,
故选:B.
根据矩形的性质及已知可推出是等边三角形,可得,利用三角形内角和求出,根据含30度角的直角三角形的性质以及勾股定理求得,根据矩形的面积=AB×BC进行计算即可.
24.B
解:∵一次函数的图象与轴交于点,与轴交于点,
解得
∴该函数的表达式为
故选:B.
本题考查待定系数法求一次函数的解析式.根据一次函数的图象与轴交于点,与轴交于点,将点A和点B代入函数解析式可列出方程组,解方程组可求出k和b的值,据此可求出函数解析式.
25.C
解:3 + + =10,
5 =10,
=2,
则2x=4,
x=2,
故答案为:C
由二次根式的性质“、、”可将方程左边化简得:3 + + =10,再合并同类二次根式得,5 =10,把方程两边同时平方可去掉根号,然后按照一元一次方程的解题步骤计算即可求解。
26.C
27.C
解:A、,
由长度为6、8、10的三条线段能构成直角三角形,故此选项不符合题意;
B、,
由长度为0.3、0.4、0.5的三条线段能构成直角三角形,故此选项不符合题意;
C、,
由长度为、、的三条线段不能构成直角三角形,故此选项符合题意;
D、,
由长度为1、、的三条线段能构成直角三角形,故此选项不符合题意.
故答案为:C.
根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形,据此逐一判断得出答案.
28.C
解:根据,,不能判定四边形是平行四边形,故A不符合题意;
根据,,不能判定四边形是平行四边形,故B不符合题意;
,
,,
,
,
四边形是平行四边形,故C符合题意;
根据,,不能判定四边形是平行四边形,故D不符合题意;
故选:C.
根据平行四边形的判定方法对各个选项逐一进行判断.
29.A
30.C
31.A
解∶ 在中,m,m,
根据勾股定理得, m
在中,m,m,
根据勾股定理得, m,
∴ m,
故答案为∶A.
根据勾股定理进行计算即可求出答案.
32.D
33.D
34.B
35.D
36.D
37.B
解:A、∵( )2+( )2≠( )2,∴不能构成直角三角形,故本选项不符合题意;
B、∵12+( )2=22,∴能构成直角三角形,故本选项符合题意;
C、∵22+( )2≠42,∴不能构成直角三角形,故本选项不符合题意;
D、∵92+162≠252,∴不能构成直角三角形,故本选项不符合题意.
故答案为:B.
根据勾股定理的逆定理逐项判定即可。
38.B
39.B
解:平均数==1,
∴ 方差==.
故答案为:B.
先求出平均数,再根据方差的定义,即可求得.
40.A
41.D
42.C
43.D
44.C
45.C
46.D
因为7出现了2次,其他数据都是出现了1次,
所以7出现的次数最多,
所以这组数据中众数是7.
故选:D.
众数是一组数据中出现次数最多的数.
47.A
48.C
49.B
解:根据题意,一次函数y=kx+b的值随x的增大而增大,即k>0,
又∵b<0,
∴这个函数的图象经过第一三四象限,
∴不经过第二象限,
故答案为:B.
根据题意,一次函数y=kx+b的值随x的增大而增大,即k>0,又因为b<0所以,这个函数的图象经过第一三四象限,不经过第二象限.
50.A
解:A、,故A符合题意;
B、,故B不符合题意;
C、,故C不符合题意;
D、不能计算,故D不符合题意;
故答案为:A
利用二次根式的除法法则进行计算,可对A作出判断;利用二次根式的性质,可对B作出判断利用同类二次根式的定义和合并同类二次根式的法则,可对D,C作出判断.
同课章节目录
