期中真题专项复习05 解答题(含解析)--2024-2025学年八年级数学下册(北师大版)
文档属性
| 名称 | 期中真题专项复习05 解答题(含解析)--2024-2025学年八年级数学下册(北师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 610.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 13:33:08 | ||
图片预览



文档简介
2024-2025学年八年级数学下册(北师大版)
期中真题专项复习05 解答题
一、解答题
1.在平面直角坐标系中, 已知一次函数y=2x+b的图象经过点A(2,5) .点在此一次函数的图象上,其横坐标为,直线上、两点间的部分(包括、两点)记为图象.
(1)求该一次函数的表达式;
(2)当图象与轴有交点时,求的取值范围;
(3)当图象最高点与最低点的纵坐标之差为时,求的值;
(4)平面内有一点,以点为对称中心构造正方形,使得轴,当图象与正方形的边有且只有一个交点时,直接写出的取值范围.
2.为加强学生安全教育,某学校组织了“安全教育”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍,购买3副乒乓球拍和1副羽毛球拍共需140元;购买2副乒乓球拍和3副羽毛球拍共需210元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元;
(2)若学校购买乒乓球拍和羽毛球拍共30副,且总费用不超过1100元,求至少购买多少副乒乓球拍.
3.如图,的对角线相交于点O,且E、F、G、H分别是的中点.
(1)求证:四边形是平行四边形;
(2)若,求的周长.
4.如图,在中,,平分,于点.若,.
(1)求的长;
(2)求的长.
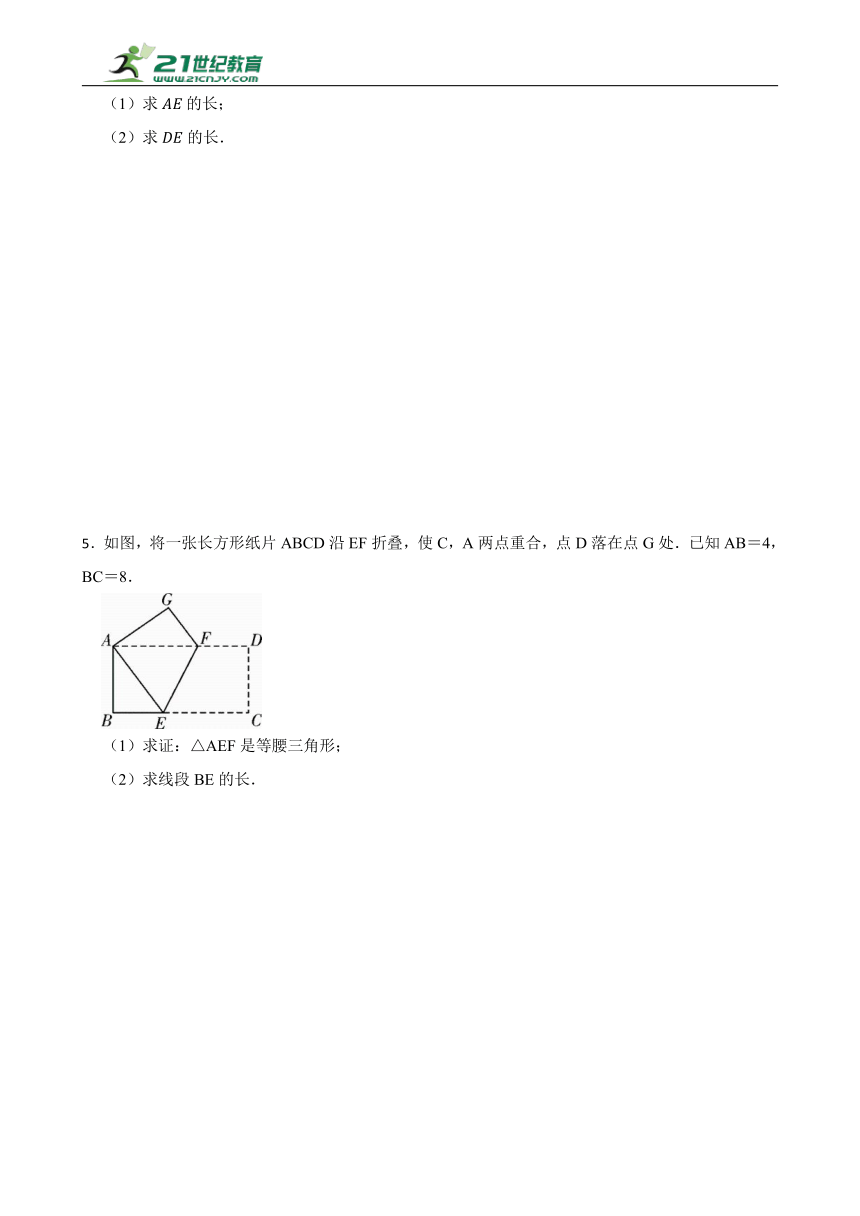
5.如图,将一张长方形纸片ABCD沿EF折叠,使C,A两点重合,点D落在点G处.已知AB=4,BC=8.
(1)求证:△AEF是等腰三角形;
(2)求线段BE的长.
6.为增强同学们垃圾分类意识,某学校举行了垃圾分类知识竞赛,一共有25道题,每一题答对得4分,答错扣1分,不答得0分.
(1)若某参赛同学只有1道题没有作答,最后他的总得分为86分,则该参赛同学一共答对了多少道题?
(2)若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“垃圾分类小达人”,则参赛者至少需答对多少道题才能被评为“垃圾分类小达人”?
7.为了强化实践育人,有效开展劳动教育和综合实践活动,我市某中学现有一块四边形的空地,如图所示,学校决定开发该空地作为学生劳动实践基地.经学校课外实践活动小组测量得到:,,,,.根据你所学过的知识,解决下列问题:
(1)四边形的面积;
(2)点D到的距离.
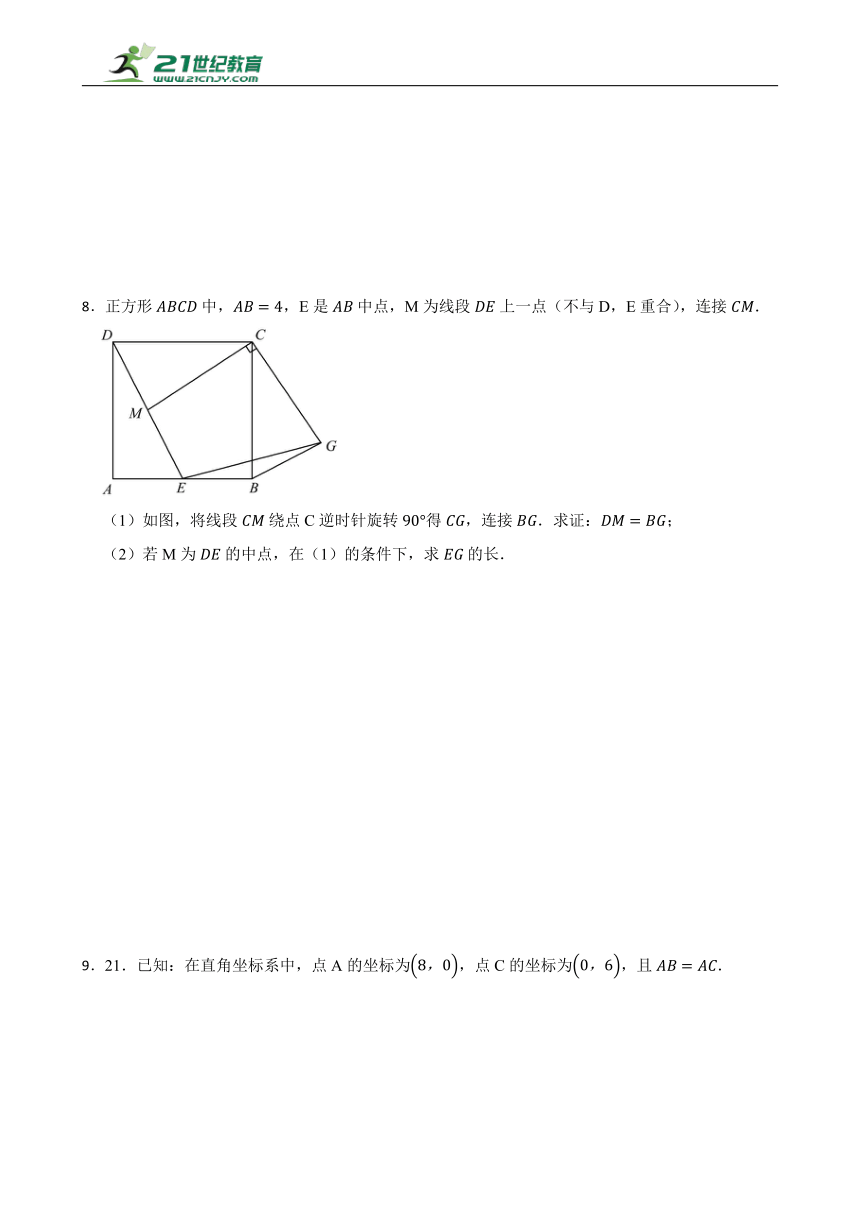
8.正方形中,,E是中点,M为线段上一点(不与D,E重合),连接.
(1)如图,将线段绕点C逆时针旋转得,连接.求证:;
(2)若M为的中点,在(1)的条件下,求的长.
9.21.已知:在直角坐标系中,点A的坐标为,点C的坐标为,且.
(1)如图①,求点B坐标;
(2)如图②,若点E为的中点,动点M从点B出发以每秒2个单位长度的速度沿线段向点A匀速运动,设点M运动的时间为t(秒);
①若的面积为1,求t的值;
②如图③,在点M运动的过程中,能否成为直角三角形?若能,直接写出此时t的值和相应的的长;若不能,请说明理由.
10.已知,在四边形中,,,,.
(1)如图1,求长.
(2)如图2,点E在的延长线上,连接,若,且四边形的面积为9.求的长.
(3)如图3,在(2)的条件下,动点P从点A出发沿以每秒0.5个单位长度的速度向终点D匀速运动,动点Q从点E出发以每秒3.5个单位长度的速度沿向终点B匀速运动.点P和点Q同时出发,当点Q到达终点停止运动时点P也随之停止运动,当运动时间t(秒)为何值时,以C、D、P、Q四点为顶点的四边形是平行四边形?
11.已知如图,直线与x轴、y轴分别交于点A、B,与直线交于点C,且.
(1)求直线的解析式及点C的坐标;
(2)将直线绕点C顺时针旋转,与x轴交于点D,与y轴交于点E,求的面积;
(3)在(2)的情况下,直线上是否存在的一个点P,使得为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
12.如图,的周长为相交于点交于点,求的周长.
13.如图,E是正方形边延长线上的一点,且.
(1)求的度数;
(2)若,求的面积.
14.如图,在四边形ABCD中,CD=AD=,∠D=90°,AB=5.BC=3.
(1)求∠C的度数;
(2)求四边形ABCD的面积.
15.如图,在中,,,,动点在边上,,动点在射线上,.
(1)若点是边上一点,在点,运动过程中,是否存在的值,使得以,,,顶点的四边形是平行四边形?若存在,求出的值;若不存在,请说明理由.
(2)如图,过点作交的延长线于点.过点作交的于点连接,把沿翻折得到,当与的一边平行时,的长______(直接写出答案)
16.某商场同时购进甲、乙两种商品共100件,其中甲商品的进价为60元,售价为80元;乙商品的进价为90元,售价为120元.设购进甲种商品x件,商场售完这100件商品的总利润为y元.
(1)写出y与x的函数关系式;
(2)该商场计划最多投入8400元购买甲、乙两种商品,若销售完这些商品,则商场可获得的最大利润是多少元
(3)商场实际进货时,生产厂家对甲种商品的出厂价下调a元(017.某礼品店经销A,B两种礼品盒,第一次购进A种礼品盒10盒,B种礼品盒15盒,共花费2800元;第二次购进A种礼品盒6盒,B种礼品盒5盒,共花费1200元
(1)求购进A,B两种礼品盒的单价分别是多少元;
(2)若该礼品店准备再次购进两种礼品盒共40盒,总费用不超过4500元,那么至少购进A种礼品盒多少盒?
18.已知关于x的一元二次方程有两个不相等的实数根.
(1)求实数m的取值范围;
(2)若m为满足条件的最大整数,求此时方程的根.
19.某学校要购买甲、乙两种消毒液,用于预防新型冠状病霉.若购买9桶甲消毒液和6桶乙消毒液,则一共需要615元:若购买8桶甲消毒液和12桶乙消毒液,则一共需要780元.
(1)每桶甲消毒液、每桶乙消毒液的价格分别是多少元?
(2)若该校计划购买甲、乙两种消毒液共30桶,其中购买甲消毒液a桶,且甲消毒液的数量至少比乙消毒液的数量多5桶,又不超过乙消毒液的数量的2倍.怎样购买.才能使总费用W最少?并求出最少费用,
20.如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
21.如图,直线分别交x轴,y轴于点,.直线分别交x轴,y轴于点C,D,与直线相交于点E,已知.
(1)求直线的表达式;
(2)求的面积;
(3)直接写出时,x的取值范围.
22. 如图,在矩形中,对角线,交于点,分别过点,作,的平行线交于点,连接交于点.
(1)求证:四边形是菱形;
(2)若,,求菱形的面积.
23.如图,在四边形中,,,动点P、Q分别从A、C同时出发,点P以的速度由A向D运动,点Q以的速度由C向B运动,其中一动点到达终点时,另一动点随之停止运动,设运动时间为t秒.
(1)__________,__________(分别用含有t的式子表示);
(2)当四边形的面积与四边形面积相等时,求出t的值;
(3)当点P、Q与四边形的任意两个顶点所组成的四边形是平行四边形时,请直接写出t的值.
24.如图,平面直角坐标系中,点O是坐标原点,是等边三角形,点A的坐标为,将绕着点A顺时针旋转,得到.
(1)求D点的坐标;
(2)连接,,求的面积.
25.如图,在中,,,BC边上的中线,求AC的长度及的面积.
26.如图,在平行四边形中,,过点D作交的延长线于点E,连接交于点F.
(1)求证:四边形是矩形;
(2)连接,若,,求的长.
27.如图,在平面直角坐标系中,一次函数为的图象经过点,且与正比例函数的图象交于点,与轴交于点C.
(1)填空:①直线的表达式为______
②当时,的取值范围是______
(2)在y轴上是否存在一点P,满足,若存在请求出点P坐标.
28.如图,直线和直线交于点,是轴上一动点,过点作平行于轴的直线,分别与直线和直线交于点.
(1)求的值;
(2)用含的式子表示线段的长;
(3)点是轴上一动点,当是等腰直角三角形时,请直接写出点的坐标.
29.如图,一条伸直的橡皮筋的两端被固定在水平桌面上,C是上的一点,,将橡皮筋从C点向上垂直拉升2到D点.
(1)求的长;
(2)判断的形状,并说明理由.
30.如图:在四边形中,,,,,.
(1)试判断的形状,并说明理由;
(2)求四边形的面积.
31.如图,在直角坐标系中,直线与x轴交于A,与直线交于,直线分别与x轴、y轴交于C、D,连接.
(1)直接根据图象写出关于x的不等式的解集;
(2)求出的值;
(3)求出的面积.
32.如图,将沿方向平移得到,若为的中点,为与的交点,,,
(1)求的长
(2)求图中阴影部分的面积
33.在平面直角坐标系中,点与点关于原点对称.
(1)求a,b的值.
(2)已知点,将点C绕原点按逆时针方向旋转后,其对应点的坐标为________.
34.如图,已知等边ABC中,BE、CD分别是AC、AB边上的中线,BE、CD相交于点O,点M、N分别为线段OB和OC中点.
(1)求证:四边形DENM是矩形;
(2)若等边ABC的边长为12,求矩形DENM的面积.
35.如图,在中,,D为边上一点,且,,点 E是边上的动点,连接.
(1)求的长;
(2)当是直角三角形时,求的长.
答案解析部分
1.(1)解:∵一次函数的图像经过点,∴,
解得:
∴该一次函数的表达式为;
(2)解:当时,,解得:
∴当图像与轴有交点时,,
∴m的取值范围为;
(3)解:当时,,即,∵,图像最高点与最低点的纵坐标之差为,
∴,
解得:或,
∴的值为或;
(4)或
(4)解:如图,由题意可知,点在直线上,
∵以点为对称中心构造正方形,轴,
∴点也在直线上,,,
∵点在一次函数的图像上,其横坐标为,
∴,
1)当点在点的上方时,此时m>2,
∵图像与正方形的边有且只有一个交点,
∴,
解得:;
2)当点在点的下方时,此时m<2,
∵图像与正方形的边有且只有一个交点,
①若点在第一象限,则
,
该不等式组的解集为空集;
②若点E在第三象限,则
,
解得:;
综上所述,的取值范围是或.
本题考查是一次函数综合题,
(1)将点代入求出的值即可;
(2)求出当时,的值即可得;
(3)先求出点的纵坐标,再根据图像最高点与最低点的纵坐标之差为建立方程,解方程即可得;
(4)分点在点的上方,点在点的下方两种情况,分别建立关于的不等式组,求解即可;根据的坐标并结合正方形的性质得到四点坐标是解题的关键.
2.(1)(1)设购买1副乒乓球拍需要x元,购买1副羽毛球拍需要y元,
由题意可得:
解得:
答:购买1副乒乓球拍需要30元,购买1副羽毛球拍需要50元;
(2)(2)设购买a副乒乓球拍,则购买(30-a)副羽毛球拍,
由题意得:30a+50(30-a)≤1100,
∴30a+15-50a ≤1100,
∴a≥20,
∵a取最小整数,
∴a=20,
答:至少要购买20副乒乓球拍.
(1)设购买1副乒乓球拍需要x元,购买1副羽毛球拍需要y元,根据题意即可列出二元一次方程组,解方程组即可得到答案;
(2)设购买a副乒乓球拍,则购买(30-a)副羽毛球拍,根据题意列出一元一次不等式,解不等式即可得到答案。
3.(1)证明:四边形是平行四边形,
,
E、F、G、H分别是的中点,
四边形是平行四边形;
(2)解:,
,
,
分别是的中点,
是的中位线,
,
的周长.
本题考查平行四边形的性质与判定,三角形的中位线及周长计算等知识。(1)由平行四边形得,根据E、F、G、H分别是的中点得EO=GO,FO=HO,可证四边形是平行四边形;(2)由得,得EF=7,则
的周长.
4.(1)
(2)的长为3
5.(1)证明:由折叠性质可知,∠AEF=∠CEF,
由题意可得AD∥BC,∴∠AFE=∠CEF.
∴∠AEF=∠AFE.∴AE=AF.
∴△AEF是等腰三角形.
(2)解:由折叠可得AE=CE,设BE=x,
则AE=CE=8-x.
∵∠B=90°,∴在Rt△ABE中,有AB2+BE2=AE2,
即42+x2=(8-x)2,解得x=3.
∴BE=3
(1)由折叠的性质得到∠AEF=∠CEF,再利用平行线的性质得到AFE=∠CEF.从而得到∠AEF=∠AFE.根据等角对等边即可求解;
(2)由折叠的性质得到AE=CE,设BE=x,AE=CE=8-x.利用勾股定理列出关于x的方程,解方程即可求解.
6.(1)解:设该同学一共答对x道题,
根据题意可得:,
解得:,
答:该参赛同学一共答对了22道题.
(2)解:设该同学至少答对x道题,
根据题意可得:,
解得:,
答:该同学至少答对23道题.
(1)设该同学一共答对x道题,根据“ 最后他的总得分为86分 ”列出方程,再求解即可;
(2)设该同学至少答对x道题,根据“ 参赛者每道题都必须作答且总得分大于或等于90分 ”列出不等式,再求解即可.
(1)设该同学一共答对x道题,
∴,
解得:,
答:该参赛同学一共答对了22道题,
(2)设该同学至少答对x道题,
,
解得:,
答:该同学至少答对23道题.
7.(1)解:连结,
在中,∵,,
∴
在中,∵,
∴
∴是直角三角形,且
∴
答:四边形的面积为.
(2)解:过点D作于点E
∵
∴;
答:点D到的距离为.
(1)连接,在中,利用勾股定理求出,再利用勾股定理的逆定理判断得到,最后利用,结合三角形面积即可求出答案.
(2)过点D作于点E,根据三角面积即可求出答案.
8.(1)证明:由题意得,,
∵正方形,
∴,,
∴,
∴,
∴;
(2)解:作交的延长线于点,取的中点,连接,
∵正方形,,E是中点,
∴,,
∴,
∵M为的中点,
∴,
∵,
∴,,
∵,
∴,
∴,
∵点是的中点,
∴是的中位线,
∴,,,
∴,
∴,
∴,,
∴,
∴.
(1)根据正方形的性质可得,,利用证明,即可证明;
(2)作交的延长线于点,取的中点,连接,先求得,由,求得,证明,求得,,,利用勾股定理可得,.
(1)证明:由题意得,,
∵正方形,
∴,,
∴,
∴,
∴;
(2)解:作交的延长线于点,取的中点,连接,如图,
∵正方形,,E是中点,
∴,,
∴,
∵M为的中点,
∴,
∵,
∴,,
∵,
∴,
∴,
∵点是的中点,
∴是的中位线,
∴,,,
∴,
∴,
∴,,
∴,
∴.
9.(1);(2)t的值为或;(3),或,.
10.(1)
(2)
(3)或时,以C、D、P、Q四点为顶点的四边形是平行四边形
11.(1),
(2)
(3)存在,点的坐标为或或或
12.
13.(1)
(2)
14.(1)135°;(2)10.
15.(1)存在,满足条件的的值为或
(2)或或
16.(1)解:由题意得y=(80-60)x+(120-90)(100-x)=-10x+3000;
(2)解: 由题意得, ,
解得 ,
随 x 增大而减小,
当 时, y最大, 最大为 ,
商场可获得的最大利润是2800元;
(3)解: 由题意得, ;
当 , 即 时, y随x增大而减小,
当 时能获得最大利润,
解得 (舍去);
当 时, 获得的利润为3000 , 不符合题意;
当 时, 则y随x增大而增大,
当 时能获得最大利润,
,
解得 ;
综上所述, .
(1)根据总利润=销售x件甲商品的利润+销售(100-x)件乙商品的利润可建立出y关于x的函数关系式;
(2)由购进x件甲商品的费用+购进(100-x)件乙商品的费用不超过8400列出不等式,求解得出x的取值范围,进而根据(1)小题所得函数解析式的性质可解此题;
(3)根据总利润=销售x件甲商品的利润+销售(100-x)件乙商品的利润可建立出y关于x的函数关系式,然后分一次项系数大于零,等于零及小于零三种情况,结合(2)中x的取值范围及一次函数的性质可解此题.
17.(1)A礼品盒的单价是100元,B礼品盒的单价是120元;
(2)至少购进A种礼品盒15盒.
18.(1)
(2)
19.(1)每桶甲消毒液的价格是45元、每桶乙消毒液的价格是35元;
(2)当甲消毒液购买18桶,乙消毒液购买12桶时,所需资金总额最少,最少总金额是1230元.
20.(1)t为5秒时,△BDE的面积为7.5cm2;(2)存在时间t为或秒时,使得△BDE与△ABC相似.
21.(1)
(2)5
(3)
22.(1)证明:,,
四边形是平行四边形,
四边形是矩形,
,
四边形是菱形;
(2)解:四边形是矩形,,
,
,
是等边三角形,
,
四边形是菱形,
,,
,
在中,根据勾股定理得,
,
,
菱形的面积为.
(1)根据两组对边分别平行的四边形是平行四边形可得四边形是平行四边形,由矩形的性质可得OC=OD,然后根据一组邻边相等的平行四边形是菱形可求解;
(2)由题意易得△OCD是等边三角形,由等边三角形的性质得CD=OC,由菱形的性质可得∠DFO=90°,∠DOF=∠DOC=30°,根据30度角所对的直角边等于斜边的一半可得DF=OD,在Rt△DFO中,用勾股定理可求出OF的值,则OE=2OF,再根据菱形的面积=两对角线乘积的一半可求解.
23.(1),
(2)
(3)t的值为或3或
24.(1)D
(2)
25.解:∵AD是的BC边上的中线,,∴,
则,∴,
∴是直角三角形,且,∴,
∴,
∴.
首先根据中线的性质求出BD的长,利用勾股定理逆定理证明∠ADB=90°,再利用勾股定理计算出AC的长;最后根据三角形的面积公式计算即可.
26.(1)证明:∵ABCD为平行四边形
∴AD||BC
∵∠ACB=90°
∴∠CAD=90°
∵DE⊥BC
∴∠DEC=90°
∴ACED为矩形
(2)解:∵ABCD为平行边形,
∴BC=AD
∵ACED为矩形,
∴CE=AD,F为AE的中点
∴BC=CE
∴CF为△ABE的中位线
∴AB=2CF=10
而AC⊥BE,C为BE的中点
∴△ABE为等腰三角形
∵
∴ABE为等边三角形
∴BF⊥AE
∴AF=5,
∴BF=
(1)结合平行四边形的性质知∠ACE=∠CAD=90°,而,即可得ACED为矩形;
(2)由平行四边形和矩形的性质知△ABE为等腰三角形,结合∠ABC=60°得等边三角形,即可求BF的长.
27.(1)①;②
(2)或
28.(1)
(2)当时,;当,
(3)点的坐标是或或或或
29.(1)解:根据题意可得:,
由勾股定理得,.
(2)解:由勾股定理得, ,
∵,
∴,
∴是直角三角形.
(1)结合图形并利用勾股定理求出AD的长即可;
(2)先利用勾股定理求出DB的长,再利用勾股定理的逆定理证出是直角三角形即可.
30.(1)解:为直角三角形,理由如下:
根据题意可得
.
在中
.
所以,为直角三角形,且
(2)
(1)在Rt△ACD中利用勾股定理求出AC的长度,结合题目已知条件可得,根据勾股定理的逆定理即可求解;
(2)由图可知四边形的面积等于两个三角形的面积之和,即代入数据计算即可.
31.(1)
(2)
(3)
32.(1)
(2)
33.(1)
(2)
34.(1)解:∵BE、CD分别是 AC、AB边上的中线,
∴D、E分别为AB、AC中点,
∴DE是△ABC中位线,
∴DE=BC,DE//BC,
又∵M、N分别线段OB、OC中点,
∴MN是△OBC的中位线,
∴MN=BC,MN//BC,
∴DE=MN,DE//MN,
∴四边形DENM是平行四边形,
∵△ABC是等边三角形,且BE、CD是中线,
∴BE、CD分别平分∠ABC、∠ACB,
∴∠EBC=∠DCB= 30°,
又∵DE//MN//BC,
∴∠OMN=∠ONM=∠OED=∠ODE=30°,
∴OM=ON,OD=OE,
∴OM+OE=ON+OD,即 ME =ND,
故四边形DENM是矩形
(2)解:∵△ABC边长为12,BE为中线,∴BC=AC=12,∠BEC=90°,CE=6,
∴DE=MN=BC=6,
根据勾股定理得,
由(1)可知,OM=OE,且M为OB的中点,
∴BM=OM=OE,
∴OM=OE=,
∵四边形DENM是矩形,且∠DEO=30°,
∴∠OEN=60°,即△OEN是等边三角形,故EN=OE=2,
∴矩形DENM的面积=.
(1)根据三角形中位线的判定及性质定理得到DE=MN,DE//MN,进而推出四边形DENM是平行四边形,利用等边三角形的性质得到OM=ON,OD=OE,证得 ME =ND,即可得到结论;
(2)先根据三角形中位线的性质得出DE的长度,勾股定理求得,然后利用等边三角形的性质求出OM,证明△OEN是等边三角形,求出EN=OE=2,根据公式求出矩形DENM的面积.
35.(1)
(2)或
期中真题专项复习05 解答题
一、解答题
1.在平面直角坐标系中, 已知一次函数y=2x+b的图象经过点A(2,5) .点在此一次函数的图象上,其横坐标为,直线上、两点间的部分(包括、两点)记为图象.
(1)求该一次函数的表达式;
(2)当图象与轴有交点时,求的取值范围;
(3)当图象最高点与最低点的纵坐标之差为时,求的值;
(4)平面内有一点,以点为对称中心构造正方形,使得轴,当图象与正方形的边有且只有一个交点时,直接写出的取值范围.
2.为加强学生安全教育,某学校组织了“安全教育”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍,购买3副乒乓球拍和1副羽毛球拍共需140元;购买2副乒乓球拍和3副羽毛球拍共需210元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元;
(2)若学校购买乒乓球拍和羽毛球拍共30副,且总费用不超过1100元,求至少购买多少副乒乓球拍.
3.如图,的对角线相交于点O,且E、F、G、H分别是的中点.
(1)求证:四边形是平行四边形;
(2)若,求的周长.
4.如图,在中,,平分,于点.若,.
(1)求的长;
(2)求的长.
5.如图,将一张长方形纸片ABCD沿EF折叠,使C,A两点重合,点D落在点G处.已知AB=4,BC=8.
(1)求证:△AEF是等腰三角形;
(2)求线段BE的长.
6.为增强同学们垃圾分类意识,某学校举行了垃圾分类知识竞赛,一共有25道题,每一题答对得4分,答错扣1分,不答得0分.
(1)若某参赛同学只有1道题没有作答,最后他的总得分为86分,则该参赛同学一共答对了多少道题?
(2)若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“垃圾分类小达人”,则参赛者至少需答对多少道题才能被评为“垃圾分类小达人”?
7.为了强化实践育人,有效开展劳动教育和综合实践活动,我市某中学现有一块四边形的空地,如图所示,学校决定开发该空地作为学生劳动实践基地.经学校课外实践活动小组测量得到:,,,,.根据你所学过的知识,解决下列问题:
(1)四边形的面积;
(2)点D到的距离.
8.正方形中,,E是中点,M为线段上一点(不与D,E重合),连接.
(1)如图,将线段绕点C逆时针旋转得,连接.求证:;
(2)若M为的中点,在(1)的条件下,求的长.
9.21.已知:在直角坐标系中,点A的坐标为,点C的坐标为,且.
(1)如图①,求点B坐标;
(2)如图②,若点E为的中点,动点M从点B出发以每秒2个单位长度的速度沿线段向点A匀速运动,设点M运动的时间为t(秒);
①若的面积为1,求t的值;
②如图③,在点M运动的过程中,能否成为直角三角形?若能,直接写出此时t的值和相应的的长;若不能,请说明理由.
10.已知,在四边形中,,,,.
(1)如图1,求长.
(2)如图2,点E在的延长线上,连接,若,且四边形的面积为9.求的长.
(3)如图3,在(2)的条件下,动点P从点A出发沿以每秒0.5个单位长度的速度向终点D匀速运动,动点Q从点E出发以每秒3.5个单位长度的速度沿向终点B匀速运动.点P和点Q同时出发,当点Q到达终点停止运动时点P也随之停止运动,当运动时间t(秒)为何值时,以C、D、P、Q四点为顶点的四边形是平行四边形?
11.已知如图,直线与x轴、y轴分别交于点A、B,与直线交于点C,且.
(1)求直线的解析式及点C的坐标;
(2)将直线绕点C顺时针旋转,与x轴交于点D,与y轴交于点E,求的面积;
(3)在(2)的情况下,直线上是否存在的一个点P,使得为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
12.如图,的周长为相交于点交于点,求的周长.
13.如图,E是正方形边延长线上的一点,且.
(1)求的度数;
(2)若,求的面积.
14.如图,在四边形ABCD中,CD=AD=,∠D=90°,AB=5.BC=3.
(1)求∠C的度数;
(2)求四边形ABCD的面积.
15.如图,在中,,,,动点在边上,,动点在射线上,.
(1)若点是边上一点,在点,运动过程中,是否存在的值,使得以,,,顶点的四边形是平行四边形?若存在,求出的值;若不存在,请说明理由.
(2)如图,过点作交的延长线于点.过点作交的于点连接,把沿翻折得到,当与的一边平行时,的长______(直接写出答案)
16.某商场同时购进甲、乙两种商品共100件,其中甲商品的进价为60元,售价为80元;乙商品的进价为90元,售价为120元.设购进甲种商品x件,商场售完这100件商品的总利润为y元.
(1)写出y与x的函数关系式;
(2)该商场计划最多投入8400元购买甲、乙两种商品,若销售完这些商品,则商场可获得的最大利润是多少元
(3)商场实际进货时,生产厂家对甲种商品的出厂价下调a元(0
(1)求购进A,B两种礼品盒的单价分别是多少元;
(2)若该礼品店准备再次购进两种礼品盒共40盒,总费用不超过4500元,那么至少购进A种礼品盒多少盒?
18.已知关于x的一元二次方程有两个不相等的实数根.
(1)求实数m的取值范围;
(2)若m为满足条件的最大整数,求此时方程的根.
19.某学校要购买甲、乙两种消毒液,用于预防新型冠状病霉.若购买9桶甲消毒液和6桶乙消毒液,则一共需要615元:若购买8桶甲消毒液和12桶乙消毒液,则一共需要780元.
(1)每桶甲消毒液、每桶乙消毒液的价格分别是多少元?
(2)若该校计划购买甲、乙两种消毒液共30桶,其中购买甲消毒液a桶,且甲消毒液的数量至少比乙消毒液的数量多5桶,又不超过乙消毒液的数量的2倍.怎样购买.才能使总费用W最少?并求出最少费用,
20.如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
21.如图,直线分别交x轴,y轴于点,.直线分别交x轴,y轴于点C,D,与直线相交于点E,已知.
(1)求直线的表达式;
(2)求的面积;
(3)直接写出时,x的取值范围.
22. 如图,在矩形中,对角线,交于点,分别过点,作,的平行线交于点,连接交于点.
(1)求证:四边形是菱形;
(2)若,,求菱形的面积.
23.如图,在四边形中,,,动点P、Q分别从A、C同时出发,点P以的速度由A向D运动,点Q以的速度由C向B运动,其中一动点到达终点时,另一动点随之停止运动,设运动时间为t秒.
(1)__________,__________(分别用含有t的式子表示);
(2)当四边形的面积与四边形面积相等时,求出t的值;
(3)当点P、Q与四边形的任意两个顶点所组成的四边形是平行四边形时,请直接写出t的值.
24.如图,平面直角坐标系中,点O是坐标原点,是等边三角形,点A的坐标为,将绕着点A顺时针旋转,得到.
(1)求D点的坐标;
(2)连接,,求的面积.
25.如图,在中,,,BC边上的中线,求AC的长度及的面积.
26.如图,在平行四边形中,,过点D作交的延长线于点E,连接交于点F.
(1)求证:四边形是矩形;
(2)连接,若,,求的长.
27.如图,在平面直角坐标系中,一次函数为的图象经过点,且与正比例函数的图象交于点,与轴交于点C.
(1)填空:①直线的表达式为______
②当时,的取值范围是______
(2)在y轴上是否存在一点P,满足,若存在请求出点P坐标.
28.如图,直线和直线交于点,是轴上一动点,过点作平行于轴的直线,分别与直线和直线交于点.
(1)求的值;
(2)用含的式子表示线段的长;
(3)点是轴上一动点,当是等腰直角三角形时,请直接写出点的坐标.
29.如图,一条伸直的橡皮筋的两端被固定在水平桌面上,C是上的一点,,将橡皮筋从C点向上垂直拉升2到D点.
(1)求的长;
(2)判断的形状,并说明理由.
30.如图:在四边形中,,,,,.
(1)试判断的形状,并说明理由;
(2)求四边形的面积.
31.如图,在直角坐标系中,直线与x轴交于A,与直线交于,直线分别与x轴、y轴交于C、D,连接.
(1)直接根据图象写出关于x的不等式的解集;
(2)求出的值;
(3)求出的面积.
32.如图,将沿方向平移得到,若为的中点,为与的交点,,,
(1)求的长
(2)求图中阴影部分的面积
33.在平面直角坐标系中,点与点关于原点对称.
(1)求a,b的值.
(2)已知点,将点C绕原点按逆时针方向旋转后,其对应点的坐标为________.
34.如图,已知等边ABC中,BE、CD分别是AC、AB边上的中线,BE、CD相交于点O,点M、N分别为线段OB和OC中点.
(1)求证:四边形DENM是矩形;
(2)若等边ABC的边长为12,求矩形DENM的面积.
35.如图,在中,,D为边上一点,且,,点 E是边上的动点,连接.
(1)求的长;
(2)当是直角三角形时,求的长.
答案解析部分
1.(1)解:∵一次函数的图像经过点,∴,
解得:
∴该一次函数的表达式为;
(2)解:当时,,解得:
∴当图像与轴有交点时,,
∴m的取值范围为;
(3)解:当时,,即,∵,图像最高点与最低点的纵坐标之差为,
∴,
解得:或,
∴的值为或;
(4)或
(4)解:如图,由题意可知,点在直线上,
∵以点为对称中心构造正方形,轴,
∴点也在直线上,,,
∵点在一次函数的图像上,其横坐标为,
∴,
1)当点在点的上方时,此时m>2,
∵图像与正方形的边有且只有一个交点,
∴,
解得:;
2)当点在点的下方时,此时m<2,
∵图像与正方形的边有且只有一个交点,
①若点在第一象限,则
,
该不等式组的解集为空集;
②若点E在第三象限,则
,
解得:;
综上所述,的取值范围是或.
本题考查是一次函数综合题,
(1)将点代入求出的值即可;
(2)求出当时,的值即可得;
(3)先求出点的纵坐标,再根据图像最高点与最低点的纵坐标之差为建立方程,解方程即可得;
(4)分点在点的上方,点在点的下方两种情况,分别建立关于的不等式组,求解即可;根据的坐标并结合正方形的性质得到四点坐标是解题的关键.
2.(1)(1)设购买1副乒乓球拍需要x元,购买1副羽毛球拍需要y元,
由题意可得:
解得:
答:购买1副乒乓球拍需要30元,购买1副羽毛球拍需要50元;
(2)(2)设购买a副乒乓球拍,则购买(30-a)副羽毛球拍,
由题意得:30a+50(30-a)≤1100,
∴30a+15-50a ≤1100,
∴a≥20,
∵a取最小整数,
∴a=20,
答:至少要购买20副乒乓球拍.
(1)设购买1副乒乓球拍需要x元,购买1副羽毛球拍需要y元,根据题意即可列出二元一次方程组,解方程组即可得到答案;
(2)设购买a副乒乓球拍,则购买(30-a)副羽毛球拍,根据题意列出一元一次不等式,解不等式即可得到答案。
3.(1)证明:四边形是平行四边形,
,
E、F、G、H分别是的中点,
四边形是平行四边形;
(2)解:,
,
,
分别是的中点,
是的中位线,
,
的周长.
本题考查平行四边形的性质与判定,三角形的中位线及周长计算等知识。(1)由平行四边形得,根据E、F、G、H分别是的中点得EO=GO,FO=HO,可证四边形是平行四边形;(2)由得,得EF=7,则
的周长.
4.(1)
(2)的长为3
5.(1)证明:由折叠性质可知,∠AEF=∠CEF,
由题意可得AD∥BC,∴∠AFE=∠CEF.
∴∠AEF=∠AFE.∴AE=AF.
∴△AEF是等腰三角形.
(2)解:由折叠可得AE=CE,设BE=x,
则AE=CE=8-x.
∵∠B=90°,∴在Rt△ABE中,有AB2+BE2=AE2,
即42+x2=(8-x)2,解得x=3.
∴BE=3
(1)由折叠的性质得到∠AEF=∠CEF,再利用平行线的性质得到AFE=∠CEF.从而得到∠AEF=∠AFE.根据等角对等边即可求解;
(2)由折叠的性质得到AE=CE,设BE=x,AE=CE=8-x.利用勾股定理列出关于x的方程,解方程即可求解.
6.(1)解:设该同学一共答对x道题,
根据题意可得:,
解得:,
答:该参赛同学一共答对了22道题.
(2)解:设该同学至少答对x道题,
根据题意可得:,
解得:,
答:该同学至少答对23道题.
(1)设该同学一共答对x道题,根据“ 最后他的总得分为86分 ”列出方程,再求解即可;
(2)设该同学至少答对x道题,根据“ 参赛者每道题都必须作答且总得分大于或等于90分 ”列出不等式,再求解即可.
(1)设该同学一共答对x道题,
∴,
解得:,
答:该参赛同学一共答对了22道题,
(2)设该同学至少答对x道题,
,
解得:,
答:该同学至少答对23道题.
7.(1)解:连结,
在中,∵,,
∴
在中,∵,
∴
∴是直角三角形,且
∴
答:四边形的面积为.
(2)解:过点D作于点E
∵
∴;
答:点D到的距离为.
(1)连接,在中,利用勾股定理求出,再利用勾股定理的逆定理判断得到,最后利用,结合三角形面积即可求出答案.
(2)过点D作于点E,根据三角面积即可求出答案.
8.(1)证明:由题意得,,
∵正方形,
∴,,
∴,
∴,
∴;
(2)解:作交的延长线于点,取的中点,连接,
∵正方形,,E是中点,
∴,,
∴,
∵M为的中点,
∴,
∵,
∴,,
∵,
∴,
∴,
∵点是的中点,
∴是的中位线,
∴,,,
∴,
∴,
∴,,
∴,
∴.
(1)根据正方形的性质可得,,利用证明,即可证明;
(2)作交的延长线于点,取的中点,连接,先求得,由,求得,证明,求得,,,利用勾股定理可得,.
(1)证明:由题意得,,
∵正方形,
∴,,
∴,
∴,
∴;
(2)解:作交的延长线于点,取的中点,连接,如图,
∵正方形,,E是中点,
∴,,
∴,
∵M为的中点,
∴,
∵,
∴,,
∵,
∴,
∴,
∵点是的中点,
∴是的中位线,
∴,,,
∴,
∴,
∴,,
∴,
∴.
9.(1);(2)t的值为或;(3),或,.
10.(1)
(2)
(3)或时,以C、D、P、Q四点为顶点的四边形是平行四边形
11.(1),
(2)
(3)存在,点的坐标为或或或
12.
13.(1)
(2)
14.(1)135°;(2)10.
15.(1)存在,满足条件的的值为或
(2)或或
16.(1)解:由题意得y=(80-60)x+(120-90)(100-x)=-10x+3000;
(2)解: 由题意得, ,
解得 ,
随 x 增大而减小,
当 时, y最大, 最大为 ,
商场可获得的最大利润是2800元;
(3)解: 由题意得, ;
当 , 即 时, y随x增大而减小,
当 时能获得最大利润,
解得 (舍去);
当 时, 获得的利润为3000 , 不符合题意;
当 时, 则y随x增大而增大,
当 时能获得最大利润,
,
解得 ;
综上所述, .
(1)根据总利润=销售x件甲商品的利润+销售(100-x)件乙商品的利润可建立出y关于x的函数关系式;
(2)由购进x件甲商品的费用+购进(100-x)件乙商品的费用不超过8400列出不等式,求解得出x的取值范围,进而根据(1)小题所得函数解析式的性质可解此题;
(3)根据总利润=销售x件甲商品的利润+销售(100-x)件乙商品的利润可建立出y关于x的函数关系式,然后分一次项系数大于零,等于零及小于零三种情况,结合(2)中x的取值范围及一次函数的性质可解此题.
17.(1)A礼品盒的单价是100元,B礼品盒的单价是120元;
(2)至少购进A种礼品盒15盒.
18.(1)
(2)
19.(1)每桶甲消毒液的价格是45元、每桶乙消毒液的价格是35元;
(2)当甲消毒液购买18桶,乙消毒液购买12桶时,所需资金总额最少,最少总金额是1230元.
20.(1)t为5秒时,△BDE的面积为7.5cm2;(2)存在时间t为或秒时,使得△BDE与△ABC相似.
21.(1)
(2)5
(3)
22.(1)证明:,,
四边形是平行四边形,
四边形是矩形,
,
四边形是菱形;
(2)解:四边形是矩形,,
,
,
是等边三角形,
,
四边形是菱形,
,,
,
在中,根据勾股定理得,
,
,
菱形的面积为.
(1)根据两组对边分别平行的四边形是平行四边形可得四边形是平行四边形,由矩形的性质可得OC=OD,然后根据一组邻边相等的平行四边形是菱形可求解;
(2)由题意易得△OCD是等边三角形,由等边三角形的性质得CD=OC,由菱形的性质可得∠DFO=90°,∠DOF=∠DOC=30°,根据30度角所对的直角边等于斜边的一半可得DF=OD,在Rt△DFO中,用勾股定理可求出OF的值,则OE=2OF,再根据菱形的面积=两对角线乘积的一半可求解.
23.(1),
(2)
(3)t的值为或3或
24.(1)D
(2)
25.解:∵AD是的BC边上的中线,,∴,
则,∴,
∴是直角三角形,且,∴,
∴,
∴.
首先根据中线的性质求出BD的长,利用勾股定理逆定理证明∠ADB=90°,再利用勾股定理计算出AC的长;最后根据三角形的面积公式计算即可.
26.(1)证明:∵ABCD为平行四边形
∴AD||BC
∵∠ACB=90°
∴∠CAD=90°
∵DE⊥BC
∴∠DEC=90°
∴ACED为矩形
(2)解:∵ABCD为平行边形,
∴BC=AD
∵ACED为矩形,
∴CE=AD,F为AE的中点
∴BC=CE
∴CF为△ABE的中位线
∴AB=2CF=10
而AC⊥BE,C为BE的中点
∴△ABE为等腰三角形
∵
∴ABE为等边三角形
∴BF⊥AE
∴AF=5,
∴BF=
(1)结合平行四边形的性质知∠ACE=∠CAD=90°,而,即可得ACED为矩形;
(2)由平行四边形和矩形的性质知△ABE为等腰三角形,结合∠ABC=60°得等边三角形,即可求BF的长.
27.(1)①;②
(2)或
28.(1)
(2)当时,;当,
(3)点的坐标是或或或或
29.(1)解:根据题意可得:,
由勾股定理得,.
(2)解:由勾股定理得, ,
∵,
∴,
∴是直角三角形.
(1)结合图形并利用勾股定理求出AD的长即可;
(2)先利用勾股定理求出DB的长,再利用勾股定理的逆定理证出是直角三角形即可.
30.(1)解:为直角三角形,理由如下:
根据题意可得
.
在中
.
所以,为直角三角形,且
(2)
(1)在Rt△ACD中利用勾股定理求出AC的长度,结合题目已知条件可得,根据勾股定理的逆定理即可求解;
(2)由图可知四边形的面积等于两个三角形的面积之和,即代入数据计算即可.
31.(1)
(2)
(3)
32.(1)
(2)
33.(1)
(2)
34.(1)解:∵BE、CD分别是 AC、AB边上的中线,
∴D、E分别为AB、AC中点,
∴DE是△ABC中位线,
∴DE=BC,DE//BC,
又∵M、N分别线段OB、OC中点,
∴MN是△OBC的中位线,
∴MN=BC,MN//BC,
∴DE=MN,DE//MN,
∴四边形DENM是平行四边形,
∵△ABC是等边三角形,且BE、CD是中线,
∴BE、CD分别平分∠ABC、∠ACB,
∴∠EBC=∠DCB= 30°,
又∵DE//MN//BC,
∴∠OMN=∠ONM=∠OED=∠ODE=30°,
∴OM=ON,OD=OE,
∴OM+OE=ON+OD,即 ME =ND,
故四边形DENM是矩形
(2)解:∵△ABC边长为12,BE为中线,∴BC=AC=12,∠BEC=90°,CE=6,
∴DE=MN=BC=6,
根据勾股定理得,
由(1)可知,OM=OE,且M为OB的中点,
∴BM=OM=OE,
∴OM=OE=,
∵四边形DENM是矩形,且∠DEO=30°,
∴∠OEN=60°,即△OEN是等边三角形,故EN=OE=2,
∴矩形DENM的面积=.
(1)根据三角形中位线的判定及性质定理得到DE=MN,DE//MN,进而推出四边形DENM是平行四边形,利用等边三角形的性质得到OM=ON,OD=OE,证得 ME =ND,即可得到结论;
(2)先根据三角形中位线的性质得出DE的长度,勾股定理求得,然后利用等边三角形的性质求出OM,证明△OEN是等边三角形,求出EN=OE=2,根据公式求出矩形DENM的面积.
35.(1)
(2)或
同课章节目录
